Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T15:40:06.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Experiments on flows in channels with spatially distributed heating

Published online by Cambridge University Press:  07 June 2019

A. Inasawa Open the ORCID record for A. Inasawa [Opens in a new window] ,
K. Taneda  and
J. M. Floryan Open the ORCID record for J. M. Floryan [Opens in a new window]
A. Inasawa*
Affiliation:
Department of Aeronautics and Astronautics, Tokyo Metropolitan University, Asahigaoka 6-6, Hino, Tokyo 191-0065, Japan
K. Taneda
Affiliation:
Department of Aeronautics and Astronautics, Tokyo Metropolitan University, Asahigaoka 6-6, Hino, Tokyo 191-0065, Japan
J. M. Floryan
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, Ontario N6A 5B9, Canada
*
†Email address for correspondence: ainasawa@tmu.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Flows in channels exposed to spatially distributed heating were investigated. Such flows are of interest as theoretical analyses suggest that heating leads to the reduction of pressure losses. A special apparatus providing the means for the creation of well-controlled spatially periodic heating with the desired intensity as well as precise control of the flow rate in flows with small Reynolds numbers was constructed. The apparatus works with air and provides optical access to the flow interior. The relevant theory has been generalized to handle the temperature fields measured in the experiments. The experiments were carried out for Reynolds numbers 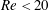$Re<20$ and at a single Rayleigh number based on the peak-to-peak temperature difference and channel half-height of 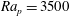$Ra_{p}=3500$. Flow visualization and particle image velocimetry measurements demonstrated the formation of two-dimensional steady rolls whose size was dictated by 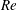$Re$, with the largest rolls observed for the smallest 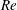$Re$ and the roll size being gradually reduced as 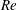$Re$ increased until their complete elimination at the largest 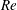$Re$ used in the experiment. An excellent agreement between the theoretically and experimentally determined complex flow fields was found. Wall shear stresses extracted from the velocity measurements agree with their theoretical counterparts within the expected accuracy. The agreement between the experimental and theoretical velocity fields and their unique relation with the corresponding pressure fields indirectly verify the heating-induced pressure-gradient-reducing effect.

JFM classification

Flow Control: Drag reduction
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 177 - 197
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aljallis, E., Sarshar, M. A., Datla, R., Sikka, V., Jones, A. & Choi, C. H. 2013 Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 25, 025103.Google Scholar
Arnal, D., Perraud, J. & Séraudie, A. 2008 Attachment line and surface imperfection problems. In Advances in Laminar–Turbulent Transition Modeling, RTO-EN-AVT-151, Brussels, Belgium. Von Karman Institute.Google Scholar
Asai, M. & Floryan, J. M. 2004 Certain aspects of channel entrance flow. Phys. Fluids 16, 1160–1163.Google Scholar
Bewley, T. R. 2009 A fundamental limit on the balance of power in a transpiration-controlled channel flow. J. Fluid Mech. 632, 443–446.Google Scholar
Bocquet, L. & Lauga, E. 2011 A smooth future? Nat. Mater. 10, 334–337.Google Scholar
Dongqing Li 2015 Encyclopedia of Microfluidics and Nanofluidics. Springer.Google Scholar
Floryan, D. & Floryan, J. M. 2015 Drag reduction in heated channels. J. Fluid Mech. 765, 353–395.Google Scholar
Floryan, J. M. 2012 The thermo-superhydrophobic effect. Bull. Am. Phys. Soc. 57, X50.00015.Google Scholar
Floryan, J. M., Shadman, S. & Hossain, M. Z. 2018 Heating-induced drag reduction in relative movement of parallel plates. Phys. Rev. Fluids 3, 094101.Google Scholar
Frőhlich, J., Laure, P. & Peyret, R. 1992 Large departures from Boussinesq approximation in the Rayleigh–Bénard problem. Phys. Fluids A 4, 1355–1372.Google Scholar
Fukunishi, Y. & Ebina, I. 2001 Active control of boundary-layer transition using a thin actuator. JSME Intl J. 44, 24–29.Google Scholar
Hœpffner, J. & Fukagata, K. 2009 Pumping or drag reduction? J. Fluid Mech. 635, 171–187.Google Scholar
Hossain, M. Z., Floryan, D. & Floryan, J. M. 2012 Drag reduction due to spatial thermal modulations. J. Fluid Mech. 713, 398–419.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2013a Heat transfer due to natural convection in a periodically heated slot. Trans. ASME J. Heat Transfer 135, 022503.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2013b Instabilities of natural convection in a periodically heated layer. J. Fluid Mech. 733, 33–67.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2014 Natural convection in a fluid layer periodically heated from above. Phys. Rev. E 90, 023015.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2015a Natural convection in a horizontal fluid layer periodically heated from above and below. Phys. Rev. E 92, 023015.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2015b Mixed convection in a periodically heated channel. J. Fluid Mech. 768, 51–90.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2016 Drag reduction in a thermally modulated channel. J. Fluid Mech. 791, 122–153.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2017 Natural convection under sub-critical conditions in the presence of heating non-uniformities. Intl J. Heat Mass Transfer 114, 8–19.Google Scholar
Inasawa, A., Ninomiya, C. & Asai, M. 2013 Suppression of tonal trailing-edge noise from an airfoil using a plasma actuator. AIAA J. 51, 1695–1702.Google Scholar
Joseph, P., Cottin-Bizonne, C., Benoit, J. M., Ybert, C., Journet, C., Tabeling, P. & Bocquet, L. 2006 Slippage of water past superhydrophobic carbon nanotube forests in microchannels. Phys. Rev. Lett. 97, 156104.Google Scholar
Kahler, J. C., Scharonowski, S. & Cierpka, C. 2012 On the uncertainty of digital PIV and PTV near walls. Exp. Fluids 52, 1641–1656.Google Scholar
Kato, T., Fukunishi, Y. & Kobayashi, R. 1997 Artificial control of the three-dimensionalization process of T–S waves in boundary-layer transition. JSME Intl J. 40, 536–541.Google Scholar
Mamori, H., Iwamoto, K. & Murata, A. 2014 Effect of the parameters of travelling waves created by blowing and suction on the relaminarization phenomena in fully developed turbulent channel flow. Phys. Fluids 26, 015101.Google Scholar
Martin, S. & Bhushan, B. 2014 Fluid flow analysis of a shark-inspired microstructure. J. Fluid Mech. 756, 5–29.Google Scholar
Min, T., Kang, S. M., Speyer, J. L. & Kim, J. 2006 Sustained sub-laminar drag in a fully developed channel flow. J. Fluid Mech. 558, 309–318.Google Scholar
Mohammadi, A. & Floryan, J. M. 2012 Mechanism of drag generation by surface corrugation. Phys. Fluids 24, 013602.Google Scholar
Mohammadi, A. & Floryan, J. M. 2013a Pressure losses in grooved channel. J. Fluid Mech. 725, 23–54.Google Scholar
Mohammadi, A. & Floryan, J. M. 2013b Groove optimization for drag reduction. Phys. Fluids 25, 113601.Google Scholar
Mohammadi, A. & Floryan, J. M. 2014 Effects of longitudinal grooves on the Couette–Poiseuille flow. J. Theor. Comput. Fluid Dyn. 28, 549–572.Google Scholar
Mohammadi, A. & Floryan, J. M. 2015 Numerical analysis of laminar-drag-reducing grooves. Trans. ASME J. Fluids Engng 137, 041201.Google Scholar
Mohammadi, A., Moradi, H. V. & Floryan, J. M. 2015 New instability mode in a grooved channel. J. Fluid Mech. 778, 691–720.Google Scholar
Moradi, H. V. & Floryan, J. M. 2013 Flows in annuli with longitudinal grooves. J. Fluid Mech. 716, 280–315.Google Scholar
Moradi, H. V. & Floryan, J. M. 2014 Stability of flow in a channel with longitudinal grooves. J. Fluid Mech. 757, 613–648.Google Scholar
Ou, J., Perot, J. B. & Rothstein, J. P. 2004 Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 16, 4635–4643.Google Scholar
Ou, J. & Rothstein, J. P. 2005 Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces. Phys. Fluids 17, 103606.Google Scholar
Paolucci, S.1982 On the filtering of sound from the Navier–Stokes equations. Report no. SAND 82-8257. Sandia National Laboratories.Google Scholar
Park, H., Park, H. & Kim, J. 2013 A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 25, 110815.Google Scholar
Park, H., Sun, G. & Kim, J. 2014 Superhydrophobic turbulent drag reduction as a function of surface grating parameters. J. Fluid Mech. 747, 722–734.Google Scholar
Poetes, R., Holtzmann, K., Franze, K. & Steiner, U. 2010 Metastable underwater superhydrophobicity. Phys. Rev. Lett. 105, 166104.Google Scholar
Quéré, D. 2008 Wetting and roughness. Annu. Rev. Mater. Res. 38, 71–99.Google Scholar
Raayai-Ardakani, S. & McKinley, G. H. 2017 Drag reduction using wrinkled surfaces in high Reynolds number laminar boundary layer flows. Phys. Fluids 29, 093605.Google Scholar
Reyssat, M., Yeomans, J. M. & Quéré, D. 2008 Impalement of fakir drops. Europhys. Lett. 81, 26006.Google Scholar
Rosenberg, B. J., Van Buren, T., Fu, M. K. & Smits, A. J. 2016 Turbulent drag reduction over air- and liquid-impregnated surfaces. Phys. Fluids 28, 015103.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Sadri, R. & Floryan, J. M. 2002a Accurate evaluation of loss coefficient and entrance length in the inlet region of a channel. Trans. ASME J. Fluids Engng 124, 685–693.Google Scholar
Sadri, R. & Floryan, J. M. 2002b Entry flow in a channel. Comput. Fluids 31, 133–157.Google Scholar
Samaha, M. A., Tafreshi, H. V. & Gad-El-Hak, M. 2011 Modeling drag reduction and meniscus stability of superhydrophobic surfaces comprised of random roughness. Phys. Fluids 23, 012001.Google Scholar
Samaha, M. A., Tafreshi, H. V. & Gad-El Hak, M. 2012 Influence of flow on longevity of superhydrophobic coatings. Langmuir 28, 9759–9766.Google Scholar
Solomon, B. R., Khalil, K. S. & Varanasi, K. K. 2014 Drag reduction using lubricant-impregnated surfaces in viscous laminar flow. Langmuir 30, 10970–10976.Google Scholar
Solomon, B. R., Khalil, K. S. & Varanasi, K. K. 2016 Correction to drag reduction using lubricant-impregnated surfaces in viscous laminar flow. Langmuir 32, 8287–8287.Google Scholar
Srinivasan, S., Choi, W., Park, K. C. L., Chhatre, S. S., Cohen, R. E. & McKinley, G. H. 2013 Drag reduction for viscous laminar flow on spray-coated non-wetting surfaces. Soft Matt. 9, 5691–5702.Google Scholar
Szumbarski, J. 2007 Instability of viscous incompressible flow in a channel with transversely corrugated walls. J. Theor. Appl. Mech. 45, 659–683.Google Scholar
Szumbarski, J., Blonski, S. & Kowalewski, T. A. 2011 Impact of transversely-oriented wall corrugation on hydraulic resistance of a channel flow. Arch. Mech. Engng 58, 441–466.Google Scholar
Truesdell, R., Mammoli, P., Vorobieff, P., van Swol, P. & Brinker, C. J. 2006 Drag reduction on a patterned superhydrophobic surface. Phys. Rev. Lett. 97, 044504.Google Scholar
Van Buren, T. & Smits, A. J. 2017 Substantial drag reduction in turbulent flow using liquid-infused surfaces. J. Fluid Mech. 827, 448–456.Google Scholar
Wong, T. S., Kang, S. H., Tang, S. K. Y., Smythe, E. J., Hatton, B. D., Grinthal, A. & Aizenberg, J. 2011 Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity. Nature 477, 443–447.Google Scholar
Yadav, N., Gepner, S. W. & Szumbarski, J. 2017 Instability in a channel with grooves parallel to the flow. Phys. Fluids 29, 084104.Google Scholar
Yadav, N., Gepner, S. W. & Szumbarski, J. 2018 Flow dynamics in longitudinally grooved duct. Phys. Fluids 30, 104105.Google Scholar
Zhou, M., Li, J., Wu, C., Zhou, X. & Cai, L. 2011 Fluid drag reduction on superhydrophobic surfaces coated with carbon nanotube forest (CNTs). Soft Matt. 7, 4391–4396.Google Scholar