Article contents
Exponential roughness layer and analytical model for turbulent boundary layer flow over rectangular-prism roughness elements
Published online by Cambridge University Press: 18 January 2016
Abstract
We conduct a series of large-eddy simulations (LES) to examine the mean flow behaviour within the roughness layer of turbulent boundary layer flow over rough surfaces. We consider several configurations consisting of arrays of rectangular-prism roughness elements with various spacings, aspect ratios and height distributions. The results provide clear evidence for exponential behaviour of the mean flow with respect to the wall normal distance. Such behaviour has been proposed before (see, e.g., Cionco, 1966 Tech. Rep. DTIC document), and is represented as 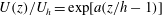 $U(z)/U_{h}=\exp [a(z/h-1)]$ , where
$U(z)/U_{h}=\exp [a(z/h-1)]$ , where 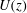 $U(z)$ is the spatially/temporally averaged fluid velocity,
$U(z)$ is the spatially/temporally averaged fluid velocity,  $z$ is the wall normal distance,
$z$ is the wall normal distance, 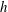 $h$ represents the height of the roughness elements and
$h$ represents the height of the roughness elements and 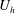 $U_{h}$ is the velocity at
$U_{h}$ is the velocity at 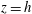 $z=h$ . The attenuation factor
$z=h$ . The attenuation factor  $a$ depends on the density of the roughness element distributionand details of the roughness distribution on the wall. Once established, the generic velocity profile shape is used to formulate a fully analytical model for the effective drag exerted by turbulent flow on a surface covered with arrays of rectangular-prism roughness elements. The approach is based on the von Karman–Pohlhausen integral method, in which a shape function is assumed for the mean velocity profile and its parameters are determined based on momentum conservation and other fundamental constraints. In order to determine the attenuation parameter
$a$ depends on the density of the roughness element distributionand details of the roughness distribution on the wall. Once established, the generic velocity profile shape is used to formulate a fully analytical model for the effective drag exerted by turbulent flow on a surface covered with arrays of rectangular-prism roughness elements. The approach is based on the von Karman–Pohlhausen integral method, in which a shape function is assumed for the mean velocity profile and its parameters are determined based on momentum conservation and other fundamental constraints. In order to determine the attenuation parameter  $a$ , wake interactions among surface roughness elements are accounted for by using the concept of flow sheltering. The model transitions smoothly between ‘
$a$ , wake interactions among surface roughness elements are accounted for by using the concept of flow sheltering. The model transitions smoothly between ‘  $k$ ’ and ‘
$k$ ’ and ‘  $d$ ’ type roughness conditions depending on the surface coverage density and the detailed geometry of roughness elements. Comparisons between model predictions and experimental/numerical data from the existing literature as well as LES data from this study are presented. It is shown that the analytical model provides good predictions of mean velocity and drag forces for the cases considered, thus raising the hope that analytical roughness modelling based on surface geometry is possible, at least for cases when the location of flow separation over surface elements can be easily predicted, as in the case of wall-attached rectangular-prism roughness elements.
$d$ ’ type roughness conditions depending on the surface coverage density and the detailed geometry of roughness elements. Comparisons between model predictions and experimental/numerical data from the existing literature as well as LES data from this study are presented. It is shown that the analytical model provides good predictions of mean velocity and drag forces for the cases considered, thus raising the hope that analytical roughness modelling based on surface geometry is possible, at least for cases when the location of flow separation over surface elements can be easily predicted, as in the case of wall-attached rectangular-prism roughness elements.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 146
- Cited by


