Hostname: page-component-76c49bb84f-lxspr Total loading time: 0 Render date: 2025-07-10T00:00:11.519Z Has data issue: false hasContentIssue false
  • English
  • Français

Filtered lifting line theory and application to the actuator line model

Published online by Cambridge University Press:  23 January 2019

Luis A. Martínez-Tossas Open the ORCID record for Luis A. Martínez-Tossas [Opens in a new window]  and
Charles Meneveau Open the ORCID record for Charles Meneveau [Opens in a new window]
Luis A. Martínez-Tossas*
Affiliation:
National Wind Technology Center, National Renewable Energy Laboratory, Golden, CO 80401-3305, USA Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Charles Meneveau
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: luis.martinez@nrel.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

Lifting line theory describes the cumulative effect of shed vorticity from finite span lifting surfaces. In this work, the theory is reformulated to improve the accuracy of the actuator line model (ALM). This model is a computational tool used to represent lifting surfaces, such as wind-turbine blades in computational fluid dynamics. In ALM, blade segments are represented by means of a Gaussian body force distribution with a prescribed kernel size. Prior analysis has shown that a representation of the blade using an optimal kernel width 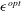$\unicode[STIX]{x1D716}^{opt}$ of approximately one quarter of the chord size results in accurate predictions of the velocity field and loads along the blades. Also, simulations have shown that use of the optimal kernel size yields accurate representation of the tip-vortex size and the associated downwash resulting in accurate predictions of the tip losses. In this work, we address the issue of how to represent the effects of finite span wings and tip vortices when using Gaussian body forces with a kernel size larger than the optimal value. This question is relevant in the context of coarse-scale large-eddy simulations that cannot afford the fine resolutions required to resolve the optimal kernel size. For this purpose, we present a filtered lifting line theory for a Gaussian force distribution. Based on the streamwise component of the vorticity transport equation, we develop an analytical model for the induced velocity resulting from the spanwise changes in lift force for an arbitrary kernel scale. The results are used to derive a subfilter-scale velocity model that is used to correct the velocity along the blade when using kernel sizes larger than 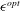$\unicode[STIX]{x1D716}^{opt}$. Tests are performed in large-eddy simulation of flow over fixed wings with constant and elliptic chord distributions using various kernel sizes. Results show that by using the proposed subfilter velocity model, kernel-size independent predictions of lift coefficient and total lift forces agree with those obtained with the optimal kernel size.

JFM classification

Mathematical Foundations: General fluid mechanics

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 269 - 292
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anderson, J. D. Jr 2010 Fundamentals of Aerodynamics. Tata McGraw-Hill Education.Google Scholar
Batchelor, G. K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.10.1017/CBO9780511800955Google Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. 2005 A scale-dependent lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17 (2), 025105.10.1063/1.1839152Google Scholar
Calaf, M., Meneveau, C. & Meyers, J. 2010 Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 22 (1), 015110.10.1063/1.3291077Google Scholar
Churchfield, M. J., Lee, S., Michalakes, J. & Moriarty, P. J. 2012 A numerical study of the effects of atmospheric and wake turbulence on wind turbine dynamics. J. Turbul. 13, N14.Google Scholar
Dag, K. O.2017 Combined pseudo-spectral/actuator line model for wind turbine applications. PhD thesis, Technical University of Denmark.Google Scholar
Dag, K. O. & Sørensen, J.2018 A new tip correction for actuator line computations (in press).Google Scholar
Forsythe, J. R., Lynch, E., Polsky, S. & Spalart, P.2015 Coupled flight simulator and CFD calculations of ship airwake using kestrel. AIAA Paper.Google Scholar
Graham, J. & Meneveau, C. 2012 Modeling turbulent flow over fractal trees using renormalized numerical simulation: alternate formulations and numerical experiments. Phys. Fluids 24 (12), 125105.10.1063/1.4772074Google Scholar
Hansen, M. O. L. 2007 Aerodynamics of Wind Turbines, 2nd edn. Routledge.Google Scholar
Ivanell, S., Sørensen, J. N. & Henningson, D. 2007 Numerical computations of wind turbine wakes. In Wind Energy, pp. 259–263. Springer.10.1007/978-3-540-33866-6_48Google Scholar
Jha, P. K., Churchfield, M. J., Moriarty, P. J. & Schmitz, S. 2014 Guidelines for volume force distributions within actuator line modeling of wind turbines on large-eddy simulation-type grids. J. Solar Energy Engng 136 (3), 031003.Google Scholar
Jonkman, J., Butterfield, S., Musial, W. & Scott, G.2009 Definition of a 5-MW reference wind turbine for offshore system development. Tech. Rep. NREL/TP-500-38060. National Renewable Energy Laboratory, Golden, CO.Google Scholar
van Kuik, G. A. M. 2018 The Fluid Dynamic Basis for Actuator Disc and Rotor Theories. IOS Press.Google Scholar
Martínez-Tossas, L. A.2017 Large eddy simulations and theoretical analysis of wind turbine aerodynamics using an actuator line model. PhD thesis, Johns Hopkins University, Baltimore, MD.Google Scholar
Martínez-Tossas, L. A., Churchfield, M. J. & Leonardi, S. 2015 Large eddy simulations of the flow past wind turbines: actuator line and disk modeling. Wind Energy 18 (6), 1047–1060.10.1002/we.1747Google Scholar
Martínez-Tossas, L. A., Churchfield, M. J. & Meneveau, C. 2016 A highly resolved large-eddy simulation of a wind turbine using an actuator line model with optimal body force projection. J. Phys.: Conf. Ser. 753, 082014.Google Scholar
Martínez-Tossas, L. A., Churchfield, M. J. & Meneveau, C. 2017 Optimal smoothing length scale for actuator line models of wind turbine blades based on Gaussian body force distribution. Wind Energy 20 (6), 1083–1096.10.1002/we.2081Google Scholar
Martínez-Tossas, L. A., Churchfield, M. J., Yilmaz, A. E., Sarlak, H., Johnson, P. L., Sørensen, J. N., Meyers, J. & Meneveau, C. 2018 Comparison of four large-eddy simulation research codes and effects of model coefficient and inflow turbulence in actuator-line-based wind turbine modeling. J. Renew. Sustainable Energy 10 (3), 033301.Google Scholar
Mikkelsen, R., Sørensen, J. N., Øye, S. & Troldborg, N. 2007 Analysis of power enhancement for a row of wind turbines using the actuator line technique. J. Phys.: Conf. Ser. 75, 012044.Google Scholar
Porté-Agel, F., Wu, Y. T., Lu, H. & Conzemius, R. J. 2011 Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind Engng Ind. Aerodyn. 99 (4), 154–168.10.1016/j.jweia.2011.01.011Google Scholar
Prandtl, L. & Tietjens, O. K. G. 1957 Applied Hydro- and Aeromechanics. Dover Publications.Google Scholar
Shives, M. & Crawford, C. 2013 Mesh and load distribution requirements for actuator line CFD simulations. Wind Energy 16 (8), 1183–1196.Google Scholar
Sørensen, J. N. & Shen, W. Z. 2002 Numerical modeling of wind turbine wakes. Trans. ASME J. Fluids Engng 124 (2), 393–399.10.1115/1.1471361Google Scholar
Stevens, R. J. A. M., Graham, J. & Meneveau, C. 2014 A concurrent precursor inflow method for large eddy simulations and applications to finite length wind farms. Renew. Energy 68, 46–50.10.1016/j.renene.2014.01.024Google Scholar
Stevens, R. J. A. M., Martínez-Tossas, L. A. & Meneveau, C. 2018 Comparison of wind farm large eddy simulations using actuator disk and actuator line models with wind tunnel experiments. Renew. Energy 116, 470–478.10.1016/j.renene.2017.08.072Google Scholar
Stewartson, K. 1960 A note on lifting line theory. Q. J. Mech. Appl. Maths 13 (1), 49–56.10.1093/qjmam/13.1.49Google Scholar
Troldborg, N., Sørensen, J. N. & Mikkelsen, R. 2010 Numerical simulations of wake characteristics of a wind turbine in uniform inflow. Wind Energy 13 (1), 86–99.10.1002/we.345Google Scholar