Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T15:39:31.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Healing of thermocapillary film rupture by viscous heating

Published online by Cambridge University Press:  10 June 2019

E. Kirkinis Open the ORCID record for E. Kirkinis [Opens in a new window]  and
A. V. Andreev
E. Kirkinis*
Affiliation:
Department of Physics, University of Washington, Seattle, WA 98195-1560, USA
A. V. Andreev
Affiliation:
Department of Physics, University of Washington, Seattle, WA 98195-1560, USA
*
†Email address for correspondence: kirkinis@uw.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Thin liquid films sitting on a heated solid substrate and surrounded by a colder ambient gas phase are strongly affected by surface-shear stresses induced by surface tension and temperature gradients, as well as by viscous and capillary forces. The temperature dependence of surface tension may lead to thinning of liquid-film depressions promoting instability which takes place when a critical temperature difference 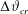$\unicode[STIX]{x0394}\unicode[STIX]{x1D717}_{cr}$ between the substrate and the ambient gas phase is exceeded. In this article we show theoretically that viscous heating, previously neglected in related literature, may delay or suppress the thermocapillary instability and leads to film healing. The viscous heating effect, by inhibiting heat transfer, prevents the system from reaching the critical value 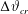$\unicode[STIX]{x0394}\unicode[STIX]{x1D717}_{cr}$ required to bring about instability. As a consequence, the system remains within the stability region, suppressing film rupture. The presence of the viscous heating effect leads to a persistent circulating motion of two counter-rotating vortices lying diametrically opposite to a depression of the liquid–gas interface reducing the wavelength of disturbances to one half of its initial value. This effect has yet to be observed in experiment.

JFM classification

Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 308 - 326
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aero, E. L., Bulygin, A. N. & Kuvshinskii, E. V. 1965 Asymmetric hydromechanics. Z. Angew. Math. Mech. 29 (2), 333–346.Google Scholar
Benney, D. J. 1966 Long waves on liquid films. J. Math. Phys. 45 (2), 150–155.Google Scholar
Braun, R. J. 2012 Dynamics of the tear film. Annu. Rev. Fluid Mech. 44, 267–297.Google Scholar
Cordero, M. L., Burnham, D. R., Baroud, C. N. & McGloin, D. 2008 Thermocapillary manipulation of droplets using holographic beam shaping: Microfluidic pin ball. Appl. Phys. Lett. 93 (3), 034107.Google Scholar
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65 (3), 851–1112.Google Scholar
Davis, M. J., Gratton, M. B. & Davis, S. H. 2010 Suppressing van der Waals driven rupture through shear. J. Fluid Mech. 661, 522–539.Google Scholar
Davis, S. H. 1987 Thermocapillary instabilities. Annu. Rev. Fluid Mech. 19 (1), 403–435.Google Scholar
Davis, S. H. 2002 Interfacial fluid dynamics. In Perspectives in Fluid Dynamics: A Collective Introduction to Current Research (ed. Batchelor, G. K., Moffatt, H. K. & Worster, M. G.), pp. 1–51. Cambridge University Press.Google Scholar
Gebhart, B. 1962 Effects of viscous dissipation in natural convection. J. Fluid Mech. 14 (2), 225–232.Google Scholar
Halpern, D. & Grotberg, J. B. 1992 Fluid-elastic instabilities of liquid-lined flexible tubes. J. Fluid Mech. 244, 615–632.Google Scholar
Huang, H., Delikanli, S., Zeng, H., Ferkey, D. M. & Pralle, A. 2010 Remote control of ion channels and neurons through magnetic-field heating of nanoparticles. Nanotechnology 5 (8), 602–606.Google Scholar
Johns, L. E. & Narayanan, R. 1997 Frictional heating in plane Couette flow. Proc. R. Soc. Lond. A 453 (1963), 1653–1670.Google Scholar
Joseph, D. D. 1965 Stability of frictionally-heated flow. Phys. Fluids 8 (12), 2195–2200.Google Scholar
Kataoka, D. E. & Troian, S. M. 1998 Stabilizing the advancing front of thermally driven climbing films. J. Colloid Interface Sci. 203 (2), 335–344.Google Scholar
Kataoka, D. E. & Troian, S. M. 1999 Patterning liquid flow on the microscopic scale. Nature 402 (6763), 794–797.Google Scholar
Kerchman, V. I. & Frenkel, A. L. 1994 Interactions of coherent structures in a film flow: simulations of a highly nonlinear evolution equation. Theor. Comput. Fluid Dyn. 6 (4), 235–254.Google Scholar
Kirkinis, E. 2017 Magnetic torque-induced suppression of van-der-Waals-driven thin liquid film rupture. J. Fluid Mech. 813, 991–1006.Google Scholar
Kirkinis, E. & Davis, S. H. 2015 Stabilization mechanisms in the evolution of thin liquid-films. Proc. R. Soc. Lond. A 471, 20150651.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1960 Electrodynamics of Continuous Media. Pergamon Press.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, Course of Theoretical Physics, vol. 6. Pergamon Press.Google Scholar
Maggi, C., Saglimbeni, F., Dipalo, M., De Angelis, F. & Di Leonardo, R. 2015 Micromotors with asymmetric shape that efficiently convert light into work by thermocapillary effects. Nat. Commun. 6, 7855.Google Scholar
Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69 (3), 931–980.Google Scholar
Polo-Corrales, L. & Rinaldi, C. 2012 Monitoring iron oxide nanoparticle surface temperature in an alternating magnetic field using thermoresponsive fluorescent polymers. J. Appl. Phys. 111 (7), 07B334.Google Scholar
Rinaldi, C.2002 Continuum modeling of polarizable systems. PhD thesis, Massachusetts Institute of Technology, Cambridge, MA.Google Scholar
Shampine, L. F. & Reichelt, M. W. 1997 The matlab ode suite. SIAM J. Sci. Comput. 18 (1), 1–22.Google Scholar
Stewart, P. S. & Davis, S. H. 2013 Self-similar coalescence of clean foams. J. Fluid Mech. 722, 645–664.Google Scholar
Subrahmaniam, N., Johns, L. E. & Narayanan, R. 2002 Stability of frictional heating in plane Couette flow at fixed power input. Proc. R. Soc. Lond. A 458 (2027), 2561–2569.Google Scholar
Turcotte, D. L., Hsui, A. T., Torrance, K. E. & Schubert, G. 1974 Influence of viscous dissipation on Bénard convection. J. Fluid Mech. 64 (2), 369–374.Google Scholar
VanHook, S. J., Schatz, M. F., Swift, J. B., McCormick, W. D. & Swinney, H. L. 1997 Long-wavelength surface-tension-driven Bénard convection: experiment and theory. J. Fluid Mech. 345, 45–78.Google Scholar
Vo, T. Q. & Kim, B.-H. 2016 Transport phenomena of water in molecular fluidic channels. Sci. Rep. 6, 33881.Google Scholar