Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-18T01:23:33.805Z Has data issue: false hasContentIssue false
  • English
  • Français

High frequency resonant response of a monopile in irregular deep water waves

Published online by Cambridge University Press:  23 August 2018

Bjørn Hervold Riise Open the ORCID record for Bjørn Hervold Riise [Opens in a new window] ,
John Grue Open the ORCID record for John Grue [Opens in a new window] ,
Atle Jensen  and
Thomas B. Johannessen
Bjørn Hervold Riise*
Affiliation:
Department of Mathematics, University of Oslo, P.O. Box 1053 Blindern, NO-0316 Oslo, Norway DNV GL Oil & Gas, PO Box 300, NO-1322 Høvik, Norway
John Grue
Affiliation:
Department of Mathematics, University of Oslo, P.O. Box 1053 Blindern, NO-0316 Oslo, Norway
Atle Jensen
Affiliation:
Department of Mathematics, University of Oslo, P.O. Box 1053 Blindern, NO-0316 Oslo, Norway
Thomas B. Johannessen
Affiliation:
DNV GL Oil & Gas, PO Box 300, NO-1322 Høvik, Norway
*
†Email address for correspondence: bjorn.riise@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

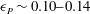Experiments with a weakly damped monopile, either fixed or free to oscillate, exposed to irregular waves in deep water, obtain the wave-exciting moment and motion response. The nonlinearity and peak wavenumber cover the ranges: $\unicode[STIX]{x1D716}_{P}\sim 0.10{-}0.14$ and 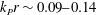$k_{P}r\sim 0.09{-}0.14$ where 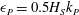$\unicode[STIX]{x1D716}_{P}=0.5H_{S}k_{P}$ is an estimate of the spectral wave slope, 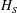$H_{S}$ the significant wave height, 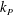$k_{P}$ the peak wavenumber and $r$ the cylinder radius. The response and its statistics, expressed in terms of the exceedance probability, are discussed as a function of the resonance frequency, 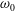$\unicode[STIX]{x1D714}_{0}$ in the range 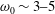$\unicode[STIX]{x1D714}_{0}\sim 3{-}5$ times the spectral peak frequency, 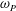$\unicode[STIX]{x1D714}_{P}$. For small wave slope, long waves and 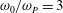$\unicode[STIX]{x1D714}_{0}/\unicode[STIX]{x1D714}_{P}=3$, the nonlinear response deviates only very little from its linear counterpart. However, the nonlinearity becomes important for increasing wave slope, wavenumber and resonance frequency ratio. The extreme response events are found in a region where the Keulegan–Carpenter number exceeds 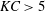$KC>5$, indicating the importance of possible flow separation effects. A similar region is also covered by a Froude number exceeding 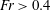$Fr>0.4$, pointing to surface gravity wave effects at the scale of the cylinder diameter. Regarding contributions to the higher harmonic forces, different wave load mechanisms are identified, including: (i) wave-exciting inertia forces, a function of the fluid acceleration; (ii) wave slamming due to both non-breaking and breaking wave events; (iii) a secondary load cycle; and (iv) possible drag forces, a function of the fluid velocity. Also, history effects due to the inertia of the moving pile, contribute to the large response events. The ensemble means of the third, fourth and fifth harmonic wave-exciting force components extracted from the irregular wave results are compared to the third harmonic FNV (Faltinsen, Newman and Vinje) theory as well as other available experiments and calculations. The present irregular wave measurements generalize results obtained in deep water regular waves.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave breaking
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 564 - 586
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bredmose, H., Slabiak, P., Sahlberg-Nielsen, L. & Schlütter, F. 2013 Dynamic excitation of monopiles by steep and breaking waves. Experimental and numerical study. In ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, vol. 8. American Society of Mechanical Engineers.Google Scholar
Chaplin, J. R., Rainey, R. C. T. & Yemm, R. W. 1997 Ringing of a vertical cylinder in waves. J. Fluid Mech. 350, 119–147.Google Scholar
Faltinsen, O. M. 1993 Sea Loads on Ships and Offshore Structures. Cambridge University Press.Google Scholar
Faltinsen, O. M., Newman, J. N. & Vinje, T. 1995 Nonlinear wave loads on a slender vertical cylinder. J. Fluid Mech. 289, 179–198.Google Scholar
Forristall, G. Z. 2000 Wave crest distributions: observations and second-order theory. J. Phys. Oceanography 30 (8), 1931–1943.Google Scholar
Goda, Y. & Suzuki, Y. 1976 Estimation of incident and reflected waves in random wave experiments. In Coastal Engineering 1976, pp. 828–845. American Society of Civil Engineers.Google Scholar
Grue, J., Bjørshol, G. & Strand, Ø. 1993 Higher harmonic wave exciting forces on a vertical cylinder. In Mechanics and Applied Mathematics, pp. 1–30. University of Oslo, Preprint series. Available at http://urn.nb.no/URN:NBN:no-52740.Google Scholar
Grue, J., Bjørshol, G. & Strand, Ø. 1994 Nonlinear wave loads which may generate ‘ringing’ responses of offshore structures. In Ninth International Workshop on Water Waves and Floating Bodies (ed. Ohkusu, M.), pp. 77–81. Kyushu University. Available at http://www.iwwwfb.org.Google Scholar
Grue, J., Clamond, D., Huseby, M. & Jensen, A. 2003 Kinematics of extreme waves in deep water. Appl. Ocean Res. 25 (6), 355–366.Google Scholar
Grue, J. & Huseby, M. 2002 Higher-harmonic wave forces and ringing of vertical cylinders. Appl. Ocean Res. 24 (4), 203–214.Google Scholar
Grue, J. & Jensen, A. 2012 Orbital velocity and breaking in steep random gravity waves. J. Geophys. Res. 117, C07013.Google Scholar
Hasselmann, K., Barnett, T. P., Bouws, E., Carlson, H., Cartwright, D. E., Enke, K., Ewing, J. A., Gienapp, H., Hasselmann, D. E., Kruseman, P., Meerburg, A., Müller, P., Olbers, D. J., Richter, K., Sell, W. & Walden, H.1973 Measurements of wind-wave growth and swell decay during the joint north sea wave project (jonswap). Tech. Rep., Deutches Hydrographisches Institut.Google Scholar
Haver, S. & Winterstein, S. R. 2009 Environmental contour lines: a method for estimating long term extremes by a short term analysis. Trans. Soc. Naval Arch. Marine Engrs 116, 116–127.Google Scholar
Huseby, M. & Grue, J. 2000 An experimental investigation of higher-harmonic wave forces on a vertical cylinder. J. Fluid Mech. 414, 75–103.Google Scholar
Johannessen, T. B. 2010 Calculations of kinematics underneath measured time histories of steep water waves. Appl. Ocean Res. 32 (4), 391–403.Google Scholar
Johannessen, T. B. 2012 Nonlinear superposition methods applied to continuous ocean wave spectra. J. Offshore Mech. Arctic Engng 134 (1), 011302.Google Scholar
Kallehave, D., Byrne, B. W., Thilsted, C. L. & Mikkelsen, K. K. 2015 Optimization of monopiles for offshore wind turbines. Phil. Trans. R. Soc. Lond. A 373 (2035), 20140100.Google Scholar
Kristiansen, T. & Faltinsen, O. M. 2017 Higher harmonic wave loads on a vertical cylinder in finite water depth. J. Fluid Mech. 833, 773–805.Google Scholar
Krokstad, J. R., Stansberg, C. T., Nestegård, A. & Marthinsen, T. 1998 A new nonslender ringing load approach verified against experiments. J. Offshore Mech. Arctic Engng 120 (1), 20–29.Google Scholar
Lighthill, J. 1979 Waves and hydrodynamic loading. In Proceedings of the Second International Conference on Behaviour of Off-Shore Structures (BOSS), pp. 1–40. BHRA Fluid Engineering.Google Scholar
Lighthill, J. 1986 Fundamentals concerning wave loading on offshore structures. J. Fluid Mech. 173, 667–681.Google Scholar
MacCamy, R. C. & Fuchs, R. A.1954 Wave forces on piles: a diffraction theory. Tech. Rep. Tech. Mem. 69. Beach Erosion Board.Google Scholar
Malenica, Š. & Molin, B. 1995 Third-harmonic wave diffraction by a vertical cylinder. J. Fluid Mech. 302, 203–229.Google Scholar
Marthinsen, T., Stansberg, C. T. & Krokstad, J. R. 1996 On the ringing excitation of circular cylinders. In The Sixth International Offshore and Polar Engineering Conference, pp. 196–204. International Society of Offshore and Polar Engineers.Google Scholar
Morison, J. R., O’Brien, M. P., Johnson, J. W. & Schaaf, S. A. 1950 The force exerted by surface waves on piles. J. Petrol. Tech. 2 (05), 149–154.Google Scholar
Newman, J. N. 1996 Nonlinear scattering of long waves by a vertical cylinder. In Waves and Nonlinear Processes in Hydrodynamics (ed. Grue, J., Gjevik, B. & Weber, J. E.), pp. 91–102. Springer.Google Scholar
Paulsen, B. T., Bredmose, H. & Bingham, H. B. 2014a An efficient domain decomposition strategy for wave loads on surface piercing circular cylinders. Coast. Engng 86, 57–76.Google Scholar
Paulsen, B. T., Bredmose, H., Bingham, H. B. & Jacobsen, N. G. 2014b Forcing of a bottom-mounted circular cylinder by steep regular water waves at finite depth. J. Fluid Mech. 755, 1–34.Google Scholar
Rainey, R. C. T. 1989 A new equation for calculating wave loads on offshore structures. J. Fluid Mech. 204, 295–324.Google Scholar
Rainey, R. C. T. 1995a The hydrodynamic load at the intersection of a cylinder with the water surface. In 10th International Workshop on Water Waves and Floating Bodies (ed. Eatock Taylor, R.), pp. 207–210. University of Oxford. Available at http://www.iwwwfb.org.Google Scholar
Rainey, R. C. T. 1995b Slender-body expressions for the wave load on offshore structures. Proc. R. Soc. Lond. A 450, 391–416.Google Scholar
Sarpkaya, T. 1986 Force on a circular cylinder in viscous oscillatory flow at low Keulegan–Carpenter numbers. J. Fluid Mech. 165, 61–71.Google Scholar
Schløer, S., Bredmose, H. & Bingham, H. B. 2016 The influence of fully nonlinear wave forces on aero–hydro–elastic calculations of monopile wind turbines. Mar. Struct. 50, 162–188.Google Scholar
Sharma, J. N. & Dean, R. G. 1981 Second-order directional seas and associated wave forces. Soc. Petrol. Engng J. 21 (01), 129–140.Google Scholar
Stansberg, C. T. 1997 Comparing ringing loads from experiments with cylinders of different diameters – an empirical study. In The Eighth Conference on the Behaviour of Offshore Structures (BOSS ’97), vol. 2, pp. 95–109. Pergamon Press.Google Scholar
Stansberg, C. T., Gudmestad, O. T. & Haver, S. K. 2008 Kinematics under extreme waves. J. Offshore Mech. Arctic Engng 130 (2), 021010.Google Scholar
Stansberg, C. T., Huse, E., Krokstad, J. R. & Lehn, E. 1995 Experimental study of non-linear loads on vertical cylinders in steep random waves. In The Fifth International Offshore and Polar Engineering Conference, pp. 75–82. International Society of Offshore and Polar Engineers.Google Scholar
Tromans, P., Swan, C. & Masterton, S.2006 Nonlinear potential flow forcing: the ringing of concrete gravity based structures. Tech. Rep. HSE Report 468, Health and Safety Executive, UK.Google Scholar
Tromans, P. S., Anaturk, A. R. & Hagemeijer, P. 1991 A new model for the kinematics of large ocean waves-application as a design wave. In The First International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers.Google Scholar
Wheeler, J. D. 1970 Methods for calculating forces produced by irregular waves. J. Petrol. Tech. 359–367.Google Scholar
Zhen, G., Bingham, H. B., Nicholls-Lee, R., Adam, F., Karmakar, D., Karr, D. G., Catipovic, I., Colicchio, G., Sheng, W., Liu, P., Takaoka, Y., Slätte, J., Shin, H., Mavrakos, S. A., Jhan, Y. & Ren, H. 2015 Offshore renewable energy. In 19th International Ship and Offshore Structures Congress, vol. 2, pp. 669–722. Taylor & Francis.Google Scholar