Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-06T21:42:00.126Z Has data issue: false hasContentIssue false
  • English
  • Français

Impact of compliant coating on Mack-mode evolution in hypersonic boundary layers

Published online by Cambridge University Press:  23 October 2023

Xiaoyang Ji ,
Ming Dong Open the ORCID record for Ming Dong [Opens in a new window]  and
Lei Zhao
Xiaoyang Ji
Affiliation:
State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China
Ming Dong*
Affiliation:
State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China
Lei Zhao*
Affiliation:
Department of Mechanics, Tianjin University, Tianjin 300072, PR China
*
†Email addresses for correspondence: dongming@imech.ac.cn, lei_zhao@tju.edu.cn
†Email addresses for correspondence: dongming@imech.ac.cn, lei_zhao@tju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

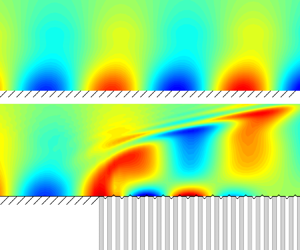
This paper focuses on the linear evolution of Mack instability modes in a hypersonic boundary layer over a flat plate that is partially coated by a compliant section. The compliant section is a thin, flexible membrane covering on a porous wall consisting of micro holes. The instability pressure could induce a vibration of the membrane, leading to a feedback to the boundary-layer fluids through the transverse velocity fluctuation. Such a process is formulated by an admittance boundary condition for the boundary-layer perturbation, which is dependent on the thickness and tension of the membrane, the properties of the porous wall, and the frequency of the Mack-mode perturbation. Using this admittance condition, the impact of the compliant coating on the Mack growth rate is studied systematically by solving the compressible Orr–Sommerfeld equations. It is found that the compliant coating could suppress the Mack instability with a frequency band in the neighbourhood of the most unstable frequency, and the stabilising frequency band widens as the membrane thickness and tension decrease, indicating a more favourable effect of a softer membrane. For a Mack mode with a specified dimensional frequency – since its dimensionless frequency, normalised by the local boundary-layer thickness and oncoming velocity, increases as it propagates downstream – the second-mode frequency band usually appears in downstream locations, and so does the stabilising effect of the membrane. Thus it is favourable to apply a compliant panel at a downstream region. In this situation, the solid–compliant junction could produce an additional scattering effect on the evolution of the Mack mode due to the sudden change of its boundary condition. The scattering effect is quantified by a transmission coefficient defined by the equivalent amplitude of the compliant-wall perturbation to the solid-wall perturbation, which can be obtained by the harmonic linearised Navier–Stokes (HLNS) approach. If the admittance is weak, then the transmission coefficient can also be predicted by an analytical solution based on the residue theorem. It is found that most of the second modes are suppressed by the scattering effect as long as the argument of the admittance is in the interval $[150^\circ, 210^\circ ]$, agreeing with most of the physical situation. The analytical predictions agree well with the HLNS calculations when the modulus of the admittance is less than $O(0.1)$.

JFM classification

Boundary Layers: Boundary layer stability Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 974 , 10 November 2023 , A1
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brès, G.A., Inkman, M., Colonius, T. & Fedorov, A.V. 2009 Alternate designs of ultrasonic absorptive coatings for hypersonic boundary layer control. AIAA Paper 2009-4217.CrossRefGoogle Scholar
Brès, G.A., Inkman, M., Colonius, T. & Fedorov, A.V. 2013 Second-mode attenuation and cancellation by porous coatings in a high-speed boundary layer. J. Fluid Mech. 726, 312–337.CrossRefGoogle Scholar
Carpenter, P.W. & Morris, P.J. 1990 The effect of anisotropic wall compliance on boundary-layer stability and transition. J. Fluid Mech. 218, 171–223.CrossRefGoogle Scholar
Chen, Y. & Scalo, C. 2021 Trapped waves in supersonic and hypersonic turbulent channel flow over porous walls. J. Fluid Mech. 920, A24.CrossRefGoogle Scholar
Chokani, N., Bountin, D.A., Shiplyuk, A.N. & Maslov, A.A. 2005 Nonlinear aspects of hypersonic boundary-layer stability on a porous surface. AIAA J. 43, 149–155.CrossRefGoogle Scholar
Chuvakhov, P. & Fedorov, A.V. 2016 Spontaneous radiation of sound by instability of a highly cooled hypersonic boundary layer. J. Fluid Mech. 805, 188–206.CrossRefGoogle Scholar
Cowley, S. & Hall, P. 1990 On the instability of hypersonic flow past a wedge. J. Fluid Mech. 214, 17–42.CrossRefGoogle Scholar
Dong, M. & Li, C. 2021 Effect of two-dimensional short rectangular indentations on hypersonic boundary-layer transition. AIAA J. 59, 2368–2381.CrossRefGoogle Scholar
Dong, M., Liu, Y. & Wu, X. 2020 Receptivity of inviscid modes in supersonic boundary layers due to scattering of free-stream sound by localised wall roughness. J. Fluid Mech. 896, A23.CrossRefGoogle Scholar
Dong, M. & Zhao, L. 2021 An asymptotic theory of the roughness impact on inviscid Mack modes in supersonic/hypersonic boundary layers. J. Fluid Mech. 913, A22.CrossRefGoogle Scholar
Egorov, I.V., Fedorov, A.V. & Soudakov, V.G. 2008 Receptivity of a hypersonic boundary layer over a flat plate with a porous coating. J. Fluid Mech. 601, 165–187.CrossRefGoogle Scholar
Fahy, F.J. 2001 Foundations of Engineering Acoustics. Elsevier.Google Scholar
Fedorov, A.V. 2003 a Receptivity of a high-speed boundary layer to acoustic disturbances. J. Fluid Mech. 491, 101–129.CrossRefGoogle Scholar
Fedorov, A.V. 2003 b Receptivity of hypersonic boundary layer to acoustic disturbances scattered by surface roughness. AIAA Paper 2003-3731.CrossRefGoogle Scholar
Fedorov, A.V. & Khokhlov, A.P. 1991 Excitation of unstable modes in a supersonic boundary layer by acoustic waves. Fluid Dyn. 9, 456–467.Google Scholar
Fedorov, A.V. & Khokhlov, A.P. 2001 Prehistory of instability in a hypersonic boundary layer. Theor. Comput. Fluid Dyn. 14, 359–375.CrossRefGoogle Scholar
Fedorov, A.V., Shiplyuk, A.N., Maslov, A.A., Burov, E.A. & Malmuth, N.D. 2003 Stabilization of a hypersonic boundary layer using an ultrasonically absorptive coating. J. Fluid Mech. 479, 99–124.CrossRefGoogle Scholar
Fong, K., Wang, X., Huang, Y., Zhong, X., McKiernan, G., Fisher, R. & Schneider, S. 2015 Second mode suppression in hypersonic boundary layer by roughness: design and experiments. AIAA J. 53, 3138–3144.CrossRefGoogle Scholar
Fong, K., Wang, X. & Zhong, X. 2014 Numerical simulation of roughness effect on the stability of a hypersonic boundary layer. Comput. Fluids 96, 350–367.CrossRefGoogle Scholar
Fujii, K. 2006 Experiment of the two-dimensional roughness effect on hypersonic boundary-layer transition. J. Spacecr. Rockets 43, 731–738.CrossRefGoogle Scholar
Gaponov, S.A. 2014 Linear instability of the supersonic boundary layer on a compliant surface. J. Appl. Math. Phys. 2, 253–263.CrossRefGoogle Scholar
Kachanov, Y.S. 1994 Physical mechanisms of laminar-boundary-layer transition. Annu. Rev. Fluid Mech. 26, 411–482.CrossRefGoogle Scholar
Li, S. & Dong, M. 2021 Verification of local scattering theory as is applied to transition prediction in hypersonic boundary layers. Adv. Mech. 51 (2), 364–375.Google Scholar
Liu, Y., Dong, M. & Wu, X. 2020 Generation of first Mack modes in supersonic boundary layers by slow acoustic waves interacting with streamwise isolated wall roughness. J. Fluid Mech. 888, A10.CrossRefGoogle Scholar
Lysenko, V.I., Gaponov, S.A., Smorodsky, B.V., Yermolaev, Y.G., Kosinov, A.D. & Semionov, N.V. 2016 Combined influence of coating permeability and roughness on supersonic boundary layer stability and transition. J. Fluid Mech. 798, 751–773.CrossRefGoogle Scholar
Mack, L. 1984 Boundary layer linear stability theory. AGARD Rep. 3–1–3–81.Google Scholar
Mack, L. 1987 Review of linear compressible stability theory. In Stability of Time Dependent and Spatially Varying Flows (ed. D.L. Dwoyer & M.Y. Hussaini), pp. 164–187. Springer.CrossRefGoogle Scholar
Malik, M. 1989 Prediction and control of transition in supersonic and hypersonic boundary layers. AIAA J. 27, 1487–1493.CrossRefGoogle Scholar
Malik, M. 1990 Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 86, 376–413.CrossRefGoogle Scholar
Masad, J.A. & Nayfeh, A.H. 1992 Laminar flow control of subsonic boundary layers by suction and heat-transfer strips. Phys. Fluids A 4, 1259–1272.CrossRefGoogle Scholar
Morkovin, M.V. 1969 Critical evaluation of transition from laminar to turbulent shear layers with emphasis on hypersonically traveling bodies. Tech. Rep. AFFDL-TR, 68-149. US Air Force Flight Dynamics Laboratory, Wright Patterson Air Force Base.Google Scholar
Rasheed, A., Hornung, H.G., Fedorov, A.V. & Malmuth, N.D. 2002 Experiments on passive hypervelocity boundary-layer control using an ultrasonically absorptive surface. AIAA J. 40, 481–489.CrossRefGoogle Scholar
Scalo, C., Bodart, J. & Lele, S.K. 2015 Compressible turbulent channel flow with impedance boundary conditions. Phys. Fluids 27 (3), 035107.CrossRefGoogle Scholar
Smith, F.T. 1986 Steady and unsteady boundary-layer separation. Annu. Rev. Fluid Mech. 18, 197–220.CrossRefGoogle Scholar
Smith, F.T. & Brown, S.N. 1990 The inviscid instability of a Blasius boundary layer at large values of the Mach number. J. Fluid Mech. 219, 499–518.CrossRefGoogle Scholar
Song, Q. & Zhao, L. 2022 Scattering of Mack modes by solid–porous junctions in hypersonic boundary layers. Phys. Fluids 34, 084104.CrossRefGoogle Scholar
Tam, C.K.W. & Auriault, L. 1996 Time-domain impedance boundary conditions for computational aeroacoustics. AIAA J. 34 (5), 917–923.CrossRefGoogle Scholar
Tijdeman, H. 1975 On the propagation of sound waves in cylindrical tubes. J. Sound Vib. 39, 1–33.CrossRefGoogle Scholar
Wu, X. & Dong, M. 2016 a Entrainment of short-wavelength free-stream vortical disturbances in compressible and incompressible boundary layers. J. Fluid Mech. 797, 683–728.CrossRefGoogle Scholar
Wu, X. & Dong, M. 2016 b A local scattering theory for the effects of isolated roughness on boundary-layer instability and transition: transmission coefficient as an eigenvalue. J. Fluid Mech. 794, 68–108.CrossRefGoogle Scholar
Zhao, L. & Dong, M. 2022 Effect of surface temperature strips on the evolution of supersonic and hypersonic Mack modes: asymptotic theory and numerical results. Phys. Rev. Fluids 7, 053901.CrossRefGoogle Scholar
Zhao, L., Dong, M. & Yang, Y. 2019 Harmonic linearized Navier–Stokes equation on describing the effect of surface roughness on hypersonic boundary-layer transition. Phys. Fluids 31, 034108.CrossRefGoogle Scholar
Zhao, L., He, J. & Dong, M. 2023 Asymptotic theory of Mack-mode receptivity in hypersonic boundary layers due to interaction of a heating/cooling source and a freestream sound wave. J. Fluid Mech. 963, A34.CrossRefGoogle Scholar