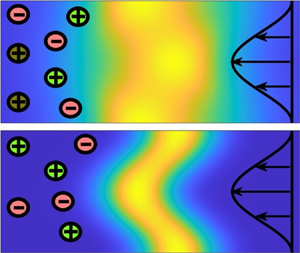
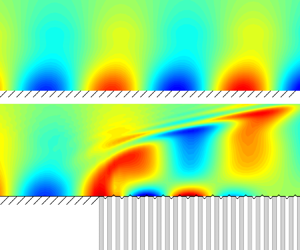
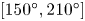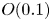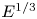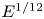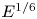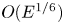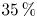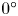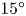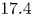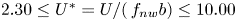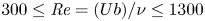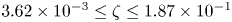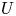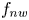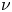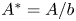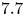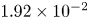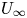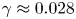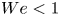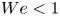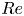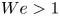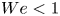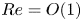doi:10.1017/jfm.2023.609 Kumar et al. Vorticity cascade and turbulent drag in wall-bounded flows: plane Poiseuille flow
JFM Rapids
Settling versus mixing in stratified shear flows
-
- Published online by Cambridge University Press:
- 26 October 2023, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Focus on Fluids
Dispersion with a pinch of salt
-
- Published online by Cambridge University Press:
- 23 October 2023, F1
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
Impact of compliant coating on Mack-mode evolution in hypersonic boundary layers
-
- Published online by Cambridge University Press:
- 23 October 2023, A1
-
- Article
- Export citation
Flow and deformation due to periodic loading in a soft porous material
-
- Published online by Cambridge University Press:
- 23 October 2023, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Internal shear layers in librating spherical shells: the case of attractors
-
- Published online by Cambridge University Press:
- 23 October 2023, A3
-
- Article
- Export citation
Slumping regime in lock-release turbidity currents
-
- Published online by Cambridge University Press:
- 23 October 2023, A4
-
- Article
- Export citation
The effect of structural damping on flow-induced vibration of a thin elliptical cylinder
-
- Published online by Cambridge University Press:
- 23 October 2023, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experiment of a thermal plume on an open cylinder
-
- Published online by Cambridge University Press:
- 25 October 2023, A6
-
- Article
- Export citation
Droplet absorption and spreading into thin layers of polymer hydrogels
-
- Published online by Cambridge University Press:
- 25 October 2023, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wind-tunnel measurements of sensible turbulent heat fluxes over melting ice
-
- Published online by Cambridge University Press:
- 25 October 2023, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effects of integral length scale variations on the stall characteristics of a wing at high free-stream turbulence conditions
-
- Published online by Cambridge University Press:
- 25 October 2023, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Assessment of heat transfer and Mach number effects on high-speed turbulent boundary layers
-
- Published online by Cambridge University Press:
- 27 October 2023, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hydrodynamic irreversibility of non-Brownian suspensions in highly confined duct flow
-
- Published online by Cambridge University Press:
- 25 October 2023, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gap-modulated dynamics of flexible plates
-
- Published online by Cambridge University Press:
- 25 October 2023, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Reynolds equation for microscale lubrication between eccentric circular cylinders based on kinetic theory
-
- Published online by Cambridge University Press:
- 27 October 2023, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The influence of spectral bandwidth and shape on deep-water wave breaking onset
-
- Published online by Cambridge University Press:
- 31 October 2023, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear disturbance growth induced by viscous dissipation in Darcy–Bénard convection with throughflow
-
- Published online by Cambridge University Press:
- 31 October 2023, A15
-
- Article
- Export citation
Hydrodynamic roughness induced by a multiscale topography
-
- Published online by Cambridge University Press:
- 26 October 2023, A16
-
- Article
- Export citation
Intermittency across Reynolds numbers – the influence of large-scale shear layers on the scaling of the enstrophy and dissipation in homogenous isotropic turbulence
-
- Published online by Cambridge University Press:
- 26 October 2023, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the shapes of liquid curtains flowing from a non-vertical slot
-
- Published online by Cambridge University Press:
- 26 October 2023, A18
-
- Article
- Export citation