Article contents
Instabilities in non-ideal fluids
Published online by Cambridge University Press: 04 October 2019
Abstract
The recent study of Ren et al. (J. Fluid Mech., vol. 871, 2019, pp. 831–864) investigated the hydrodynamic linear stability of a compressible boundary layer over an insulated flat plate for a non-ideal gas (supercritical 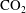 $\text{CO}_{2}$). In particular, the authors showed that in the transcritical regime (across the pseudo-critical line) the flow is strongly convectively unstable due to the co-existence of two unstable modes: Mode I, related to Tollmien–Schlichting instabilities and a new inviscid two-dimensional mode (Mode II) with a spatial growth rate one order of magnitude larger than Mode I for high Eckert numbers. In contrast to the transcritical regime, in the sub- and supercritical regimes, Mode II does not exist. Only Mode I drives the instabilities: viscous and two-dimensional for the subcritical regime and inflectional and three-dimensional for the supercritical regime.
$\text{CO}_{2}$). In particular, the authors showed that in the transcritical regime (across the pseudo-critical line) the flow is strongly convectively unstable due to the co-existence of two unstable modes: Mode I, related to Tollmien–Schlichting instabilities and a new inviscid two-dimensional mode (Mode II) with a spatial growth rate one order of magnitude larger than Mode I for high Eckert numbers. In contrast to the transcritical regime, in the sub- and supercritical regimes, Mode II does not exist. Only Mode I drives the instabilities: viscous and two-dimensional for the subcritical regime and inflectional and three-dimensional for the supercritical regime.
Information
- Type
- Focus on Fluids
- Information
- Copyright
- © 2019 Cambridge University Press
References

Figure 1. Growth rates of perturbations in the $F-Re_{\unicode[STIX]{x1D6FF}}$ stability diagram with
$T_{\infty }^{\star }=280~\text{K}$. (a)
$Ec_{\infty }=0.11,0.12,\ldots ,0.19$ (b)
$Ec_{\infty }=0.190,0.192,\ldots ,0.202$ (Mode I), (c)
$Ec_{\infty }=0.190,0.192,\ldots ,0.202$ (Mode II). From Ren et al. (2019b).


1 Introduction
Early work on instability of perfect-gas compressible boundary layers started in the 1940s (Lees & Lin Reference Lees and Lin1946), but it was with Mack’s work in the late 1960s (Mack Reference Mack1969) that the linear stability analysis of compressible boundary layers made significant progress for a wide range of Mach numbers. Several key points have been highlighted, such as the existence of multiple modes in the supersonic regime, including Mack’s mode, commonly referred to as the second mode. This mode plays a decisive role in the laminar-to-turbulent transition of an insulated boundary layer for Mach numbers greater than 4. It is strongly influenced (destabilized or stabilized) by the thermodynamic properties at the wall, as opposed to the first mode (Tollmien–Schlichting waves, TS), responsible for the transition in the subsonic regime. The prediction of this behaviour change is essential if we want to estimate the location of the laminar–turbulent transition.
The prediction of the laminar–turbulent transition is also of major concern when the fluid is working in a thermodynamic region close to the vapour–liquid critical point, at which both the liquid and gas phases of a substance have the same density, and are therefore indistinguishable. The change from a liquid-like to a gas-like behaviour occurs continuously, without boiling. This peculiar property is used in many industrial applications (Yoo Reference Yoo2013). For instance, fluids of medium to high molecular complexity are used to increase the performance of the turbine in organic Rankine cycles, where complex molecular interactions are responsible for highly non-ideal effects. Supercritical fluids, working at a pressure above the critical value, are also used to improve the efficiency of many processes, such as power cycles or refrigerating systems with supercritical $\text{CO}_{2}$
. At a given supercritical pressure, the temperature at which the transition occurs is the pseudo-critical temperature,
$\text{CO}_{2}$
. At a given supercritical pressure, the temperature at which the transition occurs is the pseudo-critical temperature,
 $T_{pc}$
, defining a line as pressure varies called the pseudo-critical or Widom line. When the fluid temperature varies through
$T_{pc}$
, defining a line as pressure varies called the pseudo-critical or Widom line. When the fluid temperature varies through
 $T_{pc}$
, large variations of thermodynamic and transport properties profoundly alter the dynamics. This is the pseudo-boiling process or transcritical regime, where the fluid behaviour departs markedly from that of the perfect-gas assumption and highly non-ideal effects can be beneficial for turbulent heat transfer characteristics. One of the challenges is then to determine how the laminar-to-turbulent transition is affected by the non-ideal effects. Despite the importance of supercritical fluids for both fundamental science and industrial applications, their flow instabilities, and more specifically the laminar-to-turbulent transition with complex or supercritical fluids working close to their critical point, remain unexplored.
$T_{pc}$
, large variations of thermodynamic and transport properties profoundly alter the dynamics. This is the pseudo-boiling process or transcritical regime, where the fluid behaviour departs markedly from that of the perfect-gas assumption and highly non-ideal effects can be beneficial for turbulent heat transfer characteristics. One of the challenges is then to determine how the laminar-to-turbulent transition is affected by the non-ideal effects. Despite the importance of supercritical fluids for both fundamental science and industrial applications, their flow instabilities, and more specifically the laminar-to-turbulent transition with complex or supercritical fluids working close to their critical point, remain unexplored.
The group around Pecnik has been interested for several years in the physical behaviour of supercritical fluids, and more recently in the instabilities developing in such fluids. In early 2019, a first paper (Ren, Fu & Pecnik Reference Ren, Fu and Pecnik2019a ) studied the linear stability of Poiseuille flows for highly non-ideal fluids (supercritical $\text{CO}_{2}$
). A strong influence of fluid properties on the linear stability of these flows was observed. The results show that the flow is more unstable in the subcritical regime compared to an ideal gas in the same conditions, but less unstable in the supercritical regime. In the transcritical regime, the flow even becomes inviscidly unstable. Ren, Marxen & Pecnik (Reference Ren, Marxen and Pecnik2019b
) have extended these results for the first time to open flows, and more specifically to boundary layer flows near the pseudo-critical line (Widom line).
$\text{CO}_{2}$
). A strong influence of fluid properties on the linear stability of these flows was observed. The results show that the flow is more unstable in the subcritical regime compared to an ideal gas in the same conditions, but less unstable in the supercritical regime. In the transcritical regime, the flow even becomes inviscidly unstable. Ren, Marxen & Pecnik (Reference Ren, Marxen and Pecnik2019b
) have extended these results for the first time to open flows, and more specifically to boundary layer flows near the pseudo-critical line (Widom line).
2 Overview
The study of linear stability of compressible boundary layers on a flat plate is not new. Motivated by applications related to the civil or military aeronautical sector, different works have very quickly sought to understand the influence of real gas effects on the stability of a boundary layer, including vibrational excitation, dissociation and recombination of gas species, ionization, radiation and surface ablation (for example, Malik & Anderson Reference Malik and Anderson1991) and thermochemical non-equilibrium reactions (for example, Stuckert & Reed Reference Stuckert and Reed1994). However, these studies do not deal with certain aspects of non-ideal gases, such as a strong thermodynamic stratification or the modification of transport properties (speed of sound, viscosity, conductivity, etc.), that occur when the fluid evolves close to the critical point. Non-ideal fluids represent a research field of great importance for a wide range of applications; the work of Ren et al. (Reference Ren, Marxen and Pecnik2019b ) aims to fill this gap.
The case of a boundary layer developing on a flat plate is considered, the gas being carbon dioxide ( $\text{CO}_{2}$
) at a supercritical pressure of 80 bar. The basic state for the stability analysis is solution of self-similar equations. The linearized equations for the perturbation are written for a strictly parallel base flow. The evolution of the dynamics is governed by various dimensionless parameters: the Reynolds, Prandtl and Mach numbers. The authors, however, point out that the Eckert number is better adapted than the Mach number to quantify the heat transfer dissipation due to friction and to the non-ideal gas effects. Ren et al. (Reference Ren, Marxen and Pecnik2019b
) showed that the non-ideal behaviour of the gas stabilizes the boundary layer in the subcritical and supercritical regimes – i.e. when the temperature profile is fully below or above the pseudo-critical temperature
$\text{CO}_{2}$
) at a supercritical pressure of 80 bar. The basic state for the stability analysis is solution of self-similar equations. The linearized equations for the perturbation are written for a strictly parallel base flow. The evolution of the dynamics is governed by various dimensionless parameters: the Reynolds, Prandtl and Mach numbers. The authors, however, point out that the Eckert number is better adapted than the Mach number to quantify the heat transfer dissipation due to friction and to the non-ideal gas effects. Ren et al. (Reference Ren, Marxen and Pecnik2019b
) showed that the non-ideal behaviour of the gas stabilizes the boundary layer in the subcritical and supercritical regimes – i.e. when the temperature profile is fully below or above the pseudo-critical temperature
 $T_{pc}=307.7~\text{K}$
, respectively. This effect is similar to that of compressibility noted in ideal gases. In the subcritical regime, the mode is two-dimensional and dominated by viscous effects (associated with TS instabilities or Mode I) while, in the supercritical regime, the mode is preferentially three-dimensional and driven by inviscid effects related to the existence of a generalized inflection point. The mode remains nonetheless linked to TS instabilities, as in the compressible regime for an ideal gas, but with a significant density fluctuation due to the non-ideal character of the gas.
$T_{pc}=307.7~\text{K}$
, respectively. This effect is similar to that of compressibility noted in ideal gases. In the subcritical regime, the mode is two-dimensional and dominated by viscous effects (associated with TS instabilities or Mode I) while, in the supercritical regime, the mode is preferentially three-dimensional and driven by inviscid effects related to the existence of a generalized inflection point. The mode remains nonetheless linked to TS instabilities, as in the compressible regime for an ideal gas, but with a significant density fluctuation due to the non-ideal character of the gas.
The most interesting and original set of results obtained by Ren et al. (Reference Ren, Marxen and Pecnik2019b ) is in the transcritical regime. Indeed, in this regime, where the temperature profile crosses the pseudo-critical line, Ren et al. (Reference Ren, Marxen and Pecnik2019b ) showed that the flow is highly destabilized through a new unstable mode (Mode II) found in addition to the conventional mode (Mode I).
Although Mode I is non-monotonic with the Eckert number $Ec_{\infty }$
, compressibility and non-ideal effects end up weakening this mode. When
$Ec_{\infty }$
, compressibility and non-ideal effects end up weakening this mode. When
 $Ec_{\infty }\geqslant 0.19$
, Mode II emerges and finally dominates. Direct numerical simulations were used to validate these observations, and the two modes were seen to co-exist transiently over a range of Eckert numbers. By an analysis similar to that of Mack (Reference Mack1984), Ren et al. (Reference Ren, Marxen and Pecnik2019b
) showed that Mode II is not connected to Mack’s second mode since the Mach number relative to the wave speed is not supersonic in the transcritical regime, which is a necessary condition to have acoustic modes such as Mack’s second mode. Nevertheless, by an extension to non-ideal gases of the generalized Rayleigh theorem, Ren et al. (Reference Ren, Marxen and Pecnik2019b
) demonstrated that Mode II is of inviscid nature. This result is the highlight of this work. Figure 1 summarizes the evolution of the different neutral curves for Modes I and II in the plane
$Ec_{\infty }\geqslant 0.19$
, Mode II emerges and finally dominates. Direct numerical simulations were used to validate these observations, and the two modes were seen to co-exist transiently over a range of Eckert numbers. By an analysis similar to that of Mack (Reference Mack1984), Ren et al. (Reference Ren, Marxen and Pecnik2019b
) showed that Mode II is not connected to Mack’s second mode since the Mach number relative to the wave speed is not supersonic in the transcritical regime, which is a necessary condition to have acoustic modes such as Mack’s second mode. Nevertheless, by an extension to non-ideal gases of the generalized Rayleigh theorem, Ren et al. (Reference Ren, Marxen and Pecnik2019b
) demonstrated that Mode II is of inviscid nature. This result is the highlight of this work. Figure 1 summarizes the evolution of the different neutral curves for Modes I and II in the plane
 $F{-}Re_{\unicode[STIX]{x1D6FF}}$
, where
$F{-}Re_{\unicode[STIX]{x1D6FF}}$
, where
 $F$
is the non-dimensional frequency and
$F$
is the non-dimensional frequency and
 $Re_{\unicode[STIX]{x1D6FF}}$
the Reynolds number based on the Blasius length scale, for
$Re_{\unicode[STIX]{x1D6FF}}$
the Reynolds number based on the Blasius length scale, for
 $Ec_{\infty }\in [0.11;0.202]$
.
$Ec_{\infty }\in [0.11;0.202]$
.
Figure 1. Growth rates of perturbations in the $F-Re_{\unicode[STIX]{x1D6FF}}$
stability diagram with
$F-Re_{\unicode[STIX]{x1D6FF}}$
stability diagram with
 $T_{\infty }^{\star }=280~\text{K}$
. (a)
$T_{\infty }^{\star }=280~\text{K}$
. (a)
 $Ec_{\infty }=0.11,0.12,\ldots ,0.19$
(b)
$Ec_{\infty }=0.11,0.12,\ldots ,0.19$
(b)
 $Ec_{\infty }=0.190,0.192,\ldots ,0.202$
(Mode I), (c)
$Ec_{\infty }=0.190,0.192,\ldots ,0.202$
(Mode I), (c)
 $Ec_{\infty }=0.190,0.192,\ldots ,0.202$
(Mode II). From Ren et al. (Reference Ren, Marxen and Pecnik2019b
).
$Ec_{\infty }=0.190,0.192,\ldots ,0.202$
(Mode II). From Ren et al. (Reference Ren, Marxen and Pecnik2019b
).
3 Future
The laminar–turbulent transition in boundary layers for non-ideal fluids is a very delicate and complicated process in which many instability mechanisms compete. The work of Ren et al. (Reference Ren, Marxen and Pecnik2019b ) opens interesting perspectives in the study of the dynamics of non-ideal gases. At first, it would be interesting to extend this analysis to other non-ideal gases in order to determine whether Mode II is a generic characteristic of such gases. Then, as the properties of selective noise amplifiers of these flows make their dynamics very sensitive to external forcings, it is necessary to study the different mechanisms of receptivity and synchronization of the different modes present.
Furthermore, it is well known that compressible boundary layer flows show a large amount of transient growth over a wide range of parameter values. The potential for transient growth in compressible boundary layers for non-ideal gases could be studied. In particular, what role does Mode II play in transient growth? This mode being related to stratification phenomena by density and to modifications of the transport properties, according to the literature on stratified flows (Kaminski, Caulfield & Taylor Reference Kaminski, Caulfield and Taylor2014), it is possible that in the transcritical regime the optimal perturbation is not invariant streamwise streaks but rather modulated streaks in the longitudinal direction. The laminar–turbulent transition can be a series of a few spatio-temporal bifurcations where, for each stage, complex nonlinear interactions between the different modes, unstable over a wide frequency band, are at work. It seems essential, if we want to better predict the transition for non-ideal gases, to study in more detail the different linear and nonlinear stages. In conclusion, the work done by Ren et al. (Reference Ren, Marxen and Pecnik2019b ) will help refine our understanding of the physical mechanisms at play for non-ideal fluids with strong property variations that can be used ultimately to improve the efficiency of many industrial processes.