Natural convection in an infinite horizontal layer subject to periodic heating along the lower wall has been investigated using a combination of numerical and asymptotic techniques. The heating maintains the same mean temperatures at both walls while producing sinusoidal temperature variations along one horizontal direction, with its spatial distribution characterized by the wavenumber $\alpha $ and the amplitude expressed in terms of a Rayleigh number 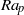$R{a}_{p} $. The primary response of the system takes the form of stationary convection consisting of rolls with the axis orthogonal to the heating wave vector and structure determined by the particular values of 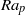$R{a}_{p} $ and $\alpha $. It is shown that for sufficiently large $\alpha $ convection is limited to a thin layer adjacent to the lower wall with a uniform conduction zone emerging above it; the temperature in this zone becomes independent of the heating pattern and varies in the vertical direction only. Linear stability of the above system has been considered and conditions leading to the emergence of secondary convection have been identified. Secondary convection gives rise to either longitudinal rolls, transverse rolls or oblique rolls at the onset, depending on $\alpha $. The longitudinal rolls are parallel to the primary rolls and the transverse rolls are orthogonal to the primary rolls, and both result in striped patterns. The oblique rolls lead to the formation of convection cells with aspect ratio dictated by their inclination angle and formation of rhombic patterns. Two mechanisms of instability have been identified. In the case of 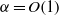$\alpha = O(1)$, parametric resonance dominates and leads to a pattern of instability that is locked in with the pattern of heating according to the relation 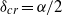${\delta }_{cr} = \alpha / 2$, where 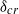${\delta }_{cr} $ denotes the component of the critical disturbance wave vector parallel to the heating wave vector. The second mechanism, the Rayleigh–Bénard (RB) mechanism, dominates for large $\alpha $, where the instability is driven by the uniform mean vertical temperature gradient created by the primary convection, with the critical disturbance wave vector 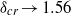${\delta }_{cr} \rightarrow 1. 56$ for 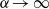$\alpha \rightarrow \infty $ and the fluid response becoming similar to that found in the case of a uniformly heated wall. Competition between these mechanisms gives rise to non-commensurable states in the case of longitudinal rolls and the appearance of soliton lattices, to the formation of distorted transverse rolls, and to the appearance of the wave vector component in the direction perpendicular to the forcing direction. A rapid stabilization is observed when the heating wavenumber is reduced below 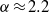$\alpha \approx 2. 2$ and no instability is found when 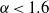$\alpha \lt 1. 6$ in the range of $R{a}_{p} $ considered. It is shown that $\alpha $ plays the role of an effective pattern control parameter and its judicious selection provides a means for the creation of a wide range of flow responses.