Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-07T07:52:54.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Internal waves generated by a stratified wake: experiment and theory

Published online by Cambridge University Press:  09 May 2018

P. Meunier Open the ORCID record for P. Meunier [Opens in a new window] ,
S. Le Dizès Open the ORCID record for S. Le Dizès [Opens in a new window] ,
L. Redekopp  and
G. R. Spedding
P. Meunier*
Affiliation:
AME Department, University of Southern California, Los Angeles, CA 90089-1191, USA Aix Marseille Univ., CNRS, Centrale Marseille, IRPHE, 13384 Marseille, France
S. Le Dizès
Affiliation:
Aix Marseille Univ., CNRS, Centrale Marseille, IRPHE, 13384 Marseille, France
L. Redekopp
Affiliation:
AME Department, University of Southern California, Los Angeles, CA 90089-1191, USA
G. R. Spedding
Affiliation:
AME Department, University of Southern California, Los Angeles, CA 90089-1191, USA
*
†Email address for correspondence: meunier@irphe.univ-mrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents experimental and theoretical results on the internal waves emitted by a bluff body moving horizontally in a linearly stratified fluid. Three different bluff bodies (a sphere, a spheroid and a cylinder) have been used in order to study the effect of the shape of the bluff body, although most of the results are obtained for the sphere. Two types of internal waves have been observed experimentally: large wavelength lee waves generated by the bluff body itself and small wavelength coherent wake waves generated by the turbulent wake. First, the lee waves are separated from the wake waves by averaging the experimental measurements in the frame moving with the bluff body. The velocity amplitude of the lee waves scales as the inverse of the Froude number 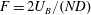$F=2U_{B}/(ND)$ for 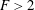$F>2$ (where 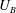$U_{B}$ is the towing velocity, 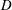$D$ the diameter and 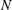$N$ the buoyancy frequency). This scaling proves that the internal waves are related to the drag of the bluff body which is due to the separation of the flow behind the bluff body. This separation is usually not taken into account in the classical models which assume that the flow is dipolar. The drag can be modelled as a point force in the Navier–Stokes equations, which gives a correct prediction of the structure and the amplitude of the lee waves. Second, the wake waves have been separated from the lee waves by averaging the velocity fields in the frame moving at the phase velocity of the waves. The phase velocity and the wavelength scale as 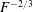$F^{-2/3}$ and 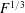$F^{1/3}$ respectively which correspond to the velocity and distance between same sign vortices of the von Kármán vortex street. A simplified model is derived for the internal waves emitted by the double row of moving point vortices of the von Kármán street. The amplitude of the wake waves is measured experimentally and seems to depend on the Reynolds number.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 846 , 10 July 2018 , pp. 752 - 788
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdilghanie, A. M. & Diamessis, P. J. 2013 The internal gravity wave field emitted by a stably stratified turbulent wake. J. Fluid Mech. 720, 104–139.Google Scholar
Baines, P. G. 1987 Upstream blocking and airflow over mountains. Annu. Rev. Fluid Mech. 19 (1), 75–95.Google Scholar
Blevins, R. 1984 Applied Fluid Dynamics Handbook. Van Nostrand Reinhold Company.Google Scholar
Bonneton, P., Chomaz, J.-M. & Hopfinger, E. J. 1993 Internal waves produced by the turbulent wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 254, 23–40.Google Scholar
Boyer, D., Davies, P., Fernando, H. & Zhang, X. 1989 Linearly stratified flow past a horizontal circular cylinder. Phil. Trans. R. Soc. Lond. A 328 (1601), 501–528.Google Scholar
Brandt, A. & Rottier, J. 2015 The internal wavefield generated by a towed sphere at low Froude number. J. Fluid Mech. 769, 103–129.Google Scholar
Chomaz, J. M., Bonneton, P., Butet, A. & Hopfinger, E. J. 1993a Vertical diffusion in the far wake of a sphere moving in a stratified fluid. Phys. Fluids A 5, 2799–2806.Google Scholar
Diamessis, P. J., Spedding, G. R. & Domaradzki, J. A. 2011 Similarity scaling and vorticity structure in high-Reynolds-number stably stratified turbulent wakes. J. Fluid Mech. 671, 52–95.Google Scholar
Dommermuth, D. G., Rottman, J. W., Innis, G. E. & Novikov, E. A. 2002 Numerical simulation of the wake of a towed sphere in a weakly stratified fluid. J. Fluid Mech. 473, 83–101.Google Scholar
Dupont, P. & Voisin, B. 1996 Internal waves generated by a translating and oscillating sphere. Dyn. Atmos. Oceans 23 (1), 289–298.Google Scholar
Fincham, A. M. & Spedding, G. R. 1997 Low-cost high-resolution DPIV for turbulent flows. Exp. Fluids 23, 449–462.Google Scholar
Gilreath, H. E. & Brandt, A. 1985 Experiments on the generation of internal waves in a stratified fluid. AIAA J. 23, 693–700.Google Scholar
Gourlay, M. J., Arendt, S. C., Fritts, D. C. & Werne, J. 2001 Numerical modeling of initially turbulent wakes with net momentum. Phys. Fluids 13, 3783–3802.Google Scholar
Hopfinger, E., Flor, J.-B., Chomaz, J.-M. & Bonneton, P. 1991 Internal waves generated by a moving sphere and its wake in a stratified fluid. Exp. Fluids 11 (4), 255–261.Google Scholar
Lighthill, M. J. 1967 On waves generated in dispersive systems by travelling forcing effects, with applications to the dynamics of rotating fluids. J. Fluid Mech. 27, 725–752.Google Scholar
Lin, J. T. & Pao, Y. H. 1979 Wakes in stratified fluids: a review. Annu. Rev. Fluid Mech. 11, 317–338.Google Scholar
Lin, Q., Boyer, D. & Fernando, H. 1993 Internal waves generated by the turbulent wake of a sphere. Exp. Fluids 15 (2), 147–154.Google Scholar
Meunier, P. 2012 Stratified wake of a tilted cylinder. Part 2. Lee internal waves. J. Fluid Mech. 699, 198–215.Google Scholar
Meunier, P., Diamessis, P. J. & Spedding, G. R. 2006 Self-preservation in stratified momentum wakes. Phys. Fluids 18 (10), 106601.Google Scholar
Meunier, P. & Spedding, G. R. 2004 A loss of memory in stratified momentum wakes. Phys. Fluids 16 (2), 298–305.Google Scholar
Milder, M.1974 Internal waves radiated by a moving source. Vol. I. Tech. Rep. No. 782-262, National Technical Information Service.Google Scholar
Miles, J. W. 1968 Lee waves in a stratified flow. Part 2. Semi-circular obstacle. J. Fluid Mech. 33 (4), 803–814.Google Scholar
Miles, J. W. 1971 Internal waves generated by a horizontally moving source. Geophys. Astrophys. Fluid Dyn. 2 (1), 63–87.Google Scholar
Munroe, J. R. & Sutherland, B. R. 2014 Internal wave energy radiated from a turbulent mixed layer. Phys. Fluids 26 (9), 096604.Google Scholar
Pal, A., Sarkar, S., Posa, A. & Balaras, E. 2017 Direct numerical simulation of stratified flow past a sphere at a subcritical Reynolds number of 3700 and moderate Froude number. J. Fluid Mech. 826, 5–31.Google Scholar
Redford, J., Lund, T. & Coleman, G. 2015 A numerical study of a weakly stratified turbulent wake. J. Fluid Mech. 776, 568–609.Google Scholar
Riley, J. R. & Lelong, M. P. 2000 Fluid motions in the presence of strong stable stratification. Annu. Rev. Fluid Mech. 32, 613.Google Scholar
Robey, H. F. 1997 The generation of internal waves by a towed sphere and its wake in a thermocline. Phys. Fluids 9 (11), 3353–3367.Google Scholar
Scase, M. & Dalziel, S. 2004 Internal wave fields and drag generated by a translating body in a stratified fluid. J. Fluid Mech. 498, 289–313.Google Scholar
Scase, M. & Dalziel, S. 2006 Internal wave fields generated by a translating body in a stratified fluid: an experimental comparison. J. Fluid Mech. 564, 305–331.Google Scholar
Spedding, G. R. 1997 The evolution of initially turbulent bluff-body wakes at high internal Froude number. J. Fluid Mech. 337, 283–301.Google Scholar
Spedding, G. R. 2002 The streamwise spacing of adjacent coherent structures in stratified wakes. Phys. Fluids 14 (11), 3820–3828.Google Scholar
Spedding, G. R. 2014 Wake signature detection. Annu. Rev. Fluid Mech. 46, 273–302.Google Scholar
Spedding, G. R., Browand, F. K., Bell, R. & Chen, J. 2000 Internal waves from intermediate, or late-wake vortices. In Stratified Flows I, Proc. 5th Int. Symp. on Stratified Flows, Vancouver Canada, UBC (ed. Lawrence, G. A., Pieters, R. & Yonemitsu, N.), pp. 113–118. University of British Columbia.Google Scholar
Spedding, G. R., Browand, F. K. & Fincham, A. M. 1996 Turbulence, similarity scaling and vortex geometry in the wake of a towed sphere in a stably stratified fluid. J. Fluid Mech. 314, 53–103.Google Scholar
de Stadler, M. B., Sarkar, S. & Brucker, K. A. 2010 Effect of the Prandtl number on a stratified turbulent wake. Phys. Fluids 22 (9), 095102.Google Scholar
Stevenson, T. & Thomas, N. 1969 Two-dimensional internal waves generated by a travelling oscillating cylinder. J. Fluid Mech. 36 (03), 505–511.Google Scholar
Stevenson, T. N. 1968 Some two-dimensional internal waves in a stratified fluid. J. Fluid Mech. 33, 715–720.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Thorpe, S. 2016 Layers and internal waves in uniformly stratified fluids stirred by vertical grids. J. Fluid Mech. 793, 380–413.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Vasholz, D. P. 2011 Stratified wakes, the high Froude number approximation, and potential flow. Theor. Comput. Fluid Dyn. 25 (6), 357–379.Google Scholar
Voisin, B. 1991 Internal wave generation in uniformly stratified fluids. Part 1. Green’s function and point sources. J. Fluid Mech. 231, 439–480.Google Scholar
Voisin, B. 1994 Internal wave generation in uniformly stratified fluids. Part 2. Moving point sources. J. Fluid Mech. 261, 333–374.Google Scholar
Voisin, B. 2007 Lee waves from a sphere in a stratified flow. J. Fluid Mech. 574, 273–315.Google Scholar
Watanabe, T., Riley, J. J., de Bruyn Kops, S. M., Diamessis, P. J. & Zhou, Q. 2016 Turbulent/non-turbulent interfaces in wakes in stably stratified fluids. J. Fluid Mech. 797, R1.Google Scholar
Zhou, Q. & Diamessis, P. J. 2016 Surface manifestation of internal waves emitted by submerged localized stratified turbulence. J. Fluid Mech. 798, 505–539.Google Scholar