Hostname: page-component-84b7d79bbc-c654p Total loading time: 0 Render date: 2024-07-28T01:15:01.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Interplay of deformability and adhesion on localization of elastic micro-particles in blood flow

Published online by Cambridge University Press:  19 December 2018

Huilin Ye ,
Zhiqiang Shen  and
Ying Li Open the ORCID record for Ying Li [Opens in a new window]
Huilin Ye
Affiliation:
Department of Mechanical Engineering, University of Connecticut, 191 Auditorium Road, Unit 3139, Storrs, CT 06269, USA
Zhiqiang Shen
Affiliation:
Department of Mechanical Engineering, University of Connecticut, 191 Auditorium Road, Unit 3139, Storrs, CT 06269, USA
Ying Li*
Affiliation:
Department of Mechanical Engineering, University of Connecticut, 191 Auditorium Road, Unit 3139, Storrs, CT 06269, USA Institute of Materials Science, University of Connecticut, 97 North Eagleville Road, Unit 3136, Storrs, CT 06269, USA
*
†Email address for correspondence: yingli@engr.uconn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The margination and adhesion of micro-particles (MPs) have been extensively investigated separately, due to their important applications in the biomedical field. However, the cascade process from margination to adhesion should play an important role in the transport of MPs in blood flow. To the best of our knowledge, this has not been explored in the past. Here we numerically study the margination behaviour of elastic MPs to blood vessel walls under the interplay of their deformability and adhesion to the vessel wall. We use the lattice Boltzmann method and molecular dynamics to solve the fluid dynamics and particle dynamics (including red blood cells (RBCs) and elastic MPs) in blood flow, respectively. Additionally, a stochastic ligand–receptor binding model is employed to capture the adhesion behaviours of elastic MPs on the vessel wall. Margination probability is used to quantify the localization of elastic MPs at the wall. Two dimensionless numbers are considered to govern the whole process: the capillary number 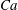$Ca$, denoting the ratio of viscous force of fluid flow to elastic interfacial force of MP, and the adhesion number $Ad$, representing the ratio of adhesion strength to viscous force of fluid flow. We systematically vary them numerically and a margination probability contour is obtained. We find that there exist two optimal regimes favouring high margination probability on the plane 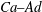$Ca{-}Ad$. The first regime, namely region I, is that with high adhesion strength and moderate particle stiffness; the other one, region II, has moderate adhesion strength and large particle stiffness. We conclude that the existence of optimal regimes is governed by the interplay of particle deformability and adhesion strength. The corresponding underlying mechanism is also discussed in detail. There are three major factors that contribute to the localization of MPs: (i) near-wall hydrodynamic collision between RBCs and MPs; (ii) deformation-induced migration due to the presence of the wall; and (iii) adhesive interaction between MPs and the wall. Mechanisms (i) and (iii) promote margination, while (ii) hampers margination. These three factors perform different roles and compete against each other when MPs are located in different regions of the flow channel, i.e. near-wall region. In optimal region I, adhesion outperforms deformation-induced migration; and in region II, the deformation-induced migration is small compared to the coupling of near-wall hydrodynamic collision and adhesion. The finding of optimal regimes can help the understanding of localization of elastic MPs at the wall under the adhesion effect in blood flow. More importantly, our results suggest that softer MP or stronger adhesion is not always the best choice for the localization of MPs.

JFM classification

Biological Fluid Dynamics: Blood flow Biological Fluid Dynamics: Capsule/cell dynamics Complex Fluids: Complex Fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 55 - 87
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abkarian, M., Lartigue, C. & Viallat, A. 2002 Tank treading and unbinding of deformable vesicles in shear flow: determination of the lift force. Phys. Rev. Lett. 88 (6), 068103.Google Scholar
Aidun, C. K. & Clausen, J. R. 2010 Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 42, 439–472.Google Scholar
Allen, M. P. & Tildesley, D. J. 1989 Computer Simulation of Liquids. Oxford University Press.Google Scholar
Balsara, H. D., Banton, R. J. & Eggleton, C. D. 2016 Investigating the effects of membrane deformability on artificial capsule adhesion to the functionalized surface. Biomech. Model. Mechanobiol. 15 (5), 1055–1068.Google Scholar
Bell, G. I. 1978 Models for the specific adhesion of cells to cells. Science 200 (4342), 618–627.Google Scholar
Benzi, R., Succi, S. & Vergassola, M. 1992 The lattice Boltzmann equation: theory and applications. Phys. Rep. 222 (3), 145–197.Google Scholar
Bernaschi, M., Melchionna, S., Succi, S., Fyta, M., Kaxiras, E. & Sircar, J. K. 2009 Muphy: a parallel multi physics/scale code for high performance bio-fluidic simulations. Comput. Phys. Commun. 180 (9), 1495–1502.Google Scholar
Bhagat, A. A. S., Bow, H., Hou, H. W., Tan, S. J., Han, J. & Lim, C. T. 2010 Microfluidics for cell separation. Med. Biol. Engng Comput. 48 (10), 999–1014.Google Scholar
Borgdorff, J., Mamonski, M., Bosak, B., Kurowski, K., Belgacem, M. B., Chopard, B., Groen, D., Coveney, P. V. & Hoekstra, A. G. 2014 Distributed multiscale computing with muscle 2, the multiscale coupling library and environment. J. Comput. Sci. 5 (5), 719–731.Google Scholar
Bretherton, F. P. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14 (2), 284–304.Google Scholar
Callens, N., Minetti, C., Coupier, G., Mader, M.-A., Dubois, F., Misbah, C. & Podgorski, T. 2008 Hydrodynamic lift of vesicles under shear flow in microgravity. Europhys. Lett. 83 (2), 24002.Google Scholar
Cantat, I. & Misbah, C. 1999 Lift force and dynamical unbinding of adhering vesicles under shear flow. Phys. Rev. Lett. 83 (4), 880.Google Scholar
Charoenphol, P., Huang, R. B. & Eniola-Adefeso, O. 2010 Potential role of size and hemodynamics in the efficacy of vascular-targeted spherical drug carriers. Biomaterials 31 (6), 1392–1402.Google Scholar
Charoenphol, P., Onyskiw, P. J., Carrasco-Teja, M. & Eniola-Adefeso, O. 2012 Particle–cell dynamics in human blood flow: implications for vascular-targeted drug delivery. J. Biomech. 45 (16), 2822–2828.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30 (1), 329–364.Google Scholar
Clausen, J. R., Reasor, D. A. Jr. & Aidun, C. K. 2010 Parallel performance of a lattice-Boltzmann/finite element cellular blood flow solver on the IBM Blue Gene/p architecture. Comput. Phys. Commun. 181 (6), 1013–1020.Google Scholar
Coclite, A., Mollica, H., Ranaldo, S., Pascazio, G., de Tullio, M. D. & Decuzzi, P. 2017 Predicting different adhesive regimens of circulating particles at blood capillary walls. Microfluid. Nanofluid. 21 (11), 168.Google Scholar
Coupier, G., Kaoui, B., Podgorski, T. & Misbah, C. 2008 Noninertial lateral migration of vesicles in bounded Poiseuille flow. Phys. Fluids 20 (11), 111702.Google Scholar
Crowl, L. & Fogelson, A. L. 2011 Analysis of mechanisms for platelet near-wall excess under arterial blood flow conditions. J. Fluid Mech. 676, 348–375.Google Scholar
Czaja, B., Závodszky, G., Tarksalooyeh, V. A. & Hoekstra, A. G. 2018 Cell-resolved blood flow simulations of saccular aneurysms: effects of pulsatility and aspect ratio. J. R. Soc. Interface 15 (146), 20180485.Google Scholar
Danker, G., Vlahovska, P. M. & Misbah, C. 2009 Vesicles in Poiseuille flow. Phys. Rev. Lett. 102 (14), 148102.Google Scholar
Dao, M., Li, J. & Suresh, S. 2006 Molecularly based analysis of deformation of spectrin network and human erythrocyte. Mater. Sci. Engng C 26 (8), 1232–1244.Google Scholar
Decuzzi, P. & Ferrari, M. 2006 The adhesive strength of non-spherical particles mediated by specific interactions. Biomaterials 27 (30), 5307–5314.Google Scholar
Decuzzi, P., Godin, B., Tanaka, T., Lee, S.-Y., Chiappini, C., Liu, X. & Ferrari, M. 2010 Size and shape effects in the biodistribution of intravascularly injected particles. J. Control. Release 141 (3), 320–327.Google Scholar
Doddi, S. K. & Bagchi, P. 2008 Lateral migration of a capsule in a plane Poiseuille flow in a channel. Intl J. Multiphase Flow 34 (10), 966–986.Google Scholar
Du Trochet, marquis, Henri 1824 Recherches Anatomiques et Physiologiques sur la Structure Intime des Animaux et des Végétaux, et sur leur Motilité. J. B. Baillière.Google Scholar
Evans, E. A. & Skalak, R. 1980 Mechanics and Thermodynamics of Biomembranes. CRC Press.Google Scholar
Fåhraeus, R. 1929 The suspension stability of the blood. Phys. Rev. 9 (2), 241–274.Google Scholar
Fåhraeus, R. & Lindqvist, T. 1931 The viscosity of the blood in narrow capillary tubes. Am. J. Phys. 96 (3), 562–568.Google Scholar
Farutin, A. & Misbah, C. 2011 Symmetry breaking of vesicle shapes in Poiseuille flow. Phys. Rev. E 84 (1), 011902.Google Scholar
Farutin, A. & Misbah, C. 2013 Analytical and numerical study of three main migration laws for vesicles under flow. Phys. Rev. Lett. 110 (10), 108104.Google Scholar
Fay, M. E., Myers, D. R., Kumar, A., Turbyfield, C. T., Byler, R., Crawford, K., Mannino, R. G., Laohapant, A., Tyburski, E. A., Sakurai, Y. et al. 2016 Cellular softening mediates leukocyte demargination and trafficking, thereby increasing clinical blood counts. Proc. Natl Acad. Sci. USA 113 (8), 1987–1992.Google Scholar
Fedosov, D. A. 2010 Multiscale Modeling of Blood Flow and Soft Matter. Brown University.Google Scholar
Fedosov, D. A., Caswell, B. & Karniadakis, G. E. 2010a A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 98 (10), 2215–2225.Google Scholar
Fedosov, D. A., Caswell, B. & Karniadakis, G. E. 2011a Wall shear stress-based model for adhesive dynamics of red blood cells in malaria. Biophys. J. 100 (9), 2084–2093.Google Scholar
Fedosov, D. A., Caswell, B., Popel, A. S. & Karniadakis, G. E. 2010b Blood flow and cell-free layer in microvessels. Microcirculation 17 (8), 615–628.Google Scholar
Fedosov, D. A., Fornleitner, J. & Gompper, G. 2012 Margination of white blood cells in microcapillary flow. Phys. Rev. Lett. 108 (2), 028104.Google Scholar
Fedosov, D. A., Pan, W., Caswell, B., Gompper, G. & Karniadakis, G. E. 2011b Predicting human blood viscosity in silico. Proc. Natl Acad. Sci. USA 108 (29), 11772–11777.Google Scholar
Fogelson, A. L. & Neeves, K. B. 2015 Fluid mechanics of blood clot formation. Annu. Rev. Fluid Mech. 47, 377–403.Google Scholar
Freund, J. B. 2007 Leukocyte margination in a model microvessel. Phys. Fluids 19 (2), 023301.Google Scholar
Gossett, D. R., Weaver, W. M., Mach, A. J., Hur, S. C., Tse, H. T. K., Lee, W., Amini, H. & Di Carlo, D. 2010 Label-free cell separation and sorting in microfluidic systems. Anal. Bioanal. Chem. 397 (8), 3249–3267.Google Scholar
Guo, Z., Zheng, C. & Shi, B. 2002 Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 65 (4), 046308.Google Scholar
de Haan, M., Zavodszky, G., Azizi, V. & Hoekstra, A. 2018 Numerical investigation of the effects of red blood cell cytoplasmic viscosity contrasts on single cell and bulk transport behaviour. Appl. Sci. 8 (9), 1616.Google Scholar
Hammer, D. A. 2014 Adhesive dynamics. Trans. ASME J. Biomech. Engng 136 (2), 021006.Google Scholar
Hammer, D. A. & Lauffenburger, D. A. 1987 A dynamical model for receptor-mediated cell adhesion to surfaces. Biophys. J. 52 (3), 475–487.Google Scholar
Higuera, F. J., Succi, S. & Benzi, R. 1989 Lattice gas dynamics with enhanced collisions. Europhys. Lett. 9 (4), 345.Google Scholar
Hou, H. W., Bhagat, A. A. S., Chong, A. G. L., Mao, P., Tan, K. S. W., Han, J. & Lim, C. T. 2010 Deformability based cell margination – simple microfluidic design for malaria-infected erythrocyte separation. Lab on a Chip 10 (19), 2605–2613.Google Scholar
Kantsler, V., Segre, E. & Steinberg, V. 2008 Dynamics of interacting vesicles and rheology of vesicle suspension in shear flow. Europhys. Lett. 82 (5), 58005.Google Scholar
Kaoui, B., Ristow, G. H., Cantat, I., Misbah, C. & Zimmermann, W. 2008 Lateral migration of a two-dimensional vesicle in unbounded Poiseuille flow. Phys. Rev. E 77 (2), 021903.Google Scholar
Katanov, D., Gompper, G. & Fedosov, D. A. 2015 Microvascular blood flow resistance: role of red blood cell migration and dispersion. Microvasc. Res. 99, 57–66.Google Scholar
Khismatullin, D. B. & Truskey, G. A. 2005 Three-dimensional numerical simulation of receptor-mediated leukocyte adhesion to surfaces: effects of cell deformability and viscoelasticity. Phys. Fluids 17 (3), 031505.Google Scholar
King, M. R. & Hammer, D. A. 2001 Multiparticle adhesive dynamics: hydrodynamic recruitment of rolling leukocytes. Proc. Natl Acad. Sci. USA 98 (26), 14919–14924.Google Scholar
Koumoutsakos, P., Pivkin, I. & Milde, F. 2013 The fluid mechanics of cancer and its therapy. Annu. Rev. Fluid Mech. 45 (1), 325–355.Google Scholar
Krüger, T., Kaoui, B. & Harting, J. 2014 Interplay of inertia and deformability on rheological properties of a suspension of capsules. J. Fluid Mech. 751, 725–745.Google Scholar
Krüger, T., Varnik, F. & Raabe, D. 2011 Efficient and accurate simulations of deformable particles immersed in a fluid using a combined immersed boundary lattice Boltzmann finite element method. Comput. Math. Appl. 61 (12), 3485–3505.Google Scholar
Kumar, A. & Graham, M. D. 2011 Segregation by membrane rigidity in flowing binary suspensions of elastic capsules. Phys. Rev. E 84 (6), 066316.Google Scholar
Kumar, A. & Graham, M. D. 2012a Margination and segregation in confined flows of blood and other multicomponent suspensions. Soft Matt. 8 (41), 10536–10548.Google Scholar
Kumar, A. & Graham, M. D. 2012b Mechanism of margination in confined flows of blood and other multicomponent suspensions. Phys. Rev. Lett. 109 (10), 108102.Google Scholar
Lee, T.-R., Choi, M., Kopacz, A. M., Yun, S.-H., Liu, W. K. & Decuzzi, P. 2013 On the near-wall accumulation of injectable particles in the microcirculation: smaller is not better. Sci. Rep. 3, 2079.Google Scholar
Ley, K. & Tedder, T. F. 1995 Leukocyte interactions with vascular endothelium. New insights into selectin-mediated attachment and rolling. J. Immunol. 155 (2), 525–528.Google Scholar
Li, Y., Lian, Y., Zhang, L. T., Aldousari, S. M., Hedia, H. S., Asiri, S. A. & Liu, W. K. 2016 Cell and nanoparticle transport in tumour microvasculature: the role of size, shape and surface functionality of nanoparticles. Interface focus 6 (1), 20150086.Google Scholar
Liu, Y. & Liu, W. K. 2006 Rheology of red blood cell aggregation by computer simulation. J. Comput. Phys. 220 (1), 139–154.Google Scholar
Loewenberg, M. & Hinch, E. J. 1997 Collision of two deformable drops in shear flow. J. Fluid Mech. 338, 299–315.Google Scholar
Lorenz, E., Hoekstra, A. G. & Caiazzo, A. 2009 Lees–Edwards boundary conditions for lattice Boltzmann suspension simulations. Phys. Rev. E 79 (3), 036706.Google Scholar
Luo, Z. Y. & Bai, B. F. 2016 State diagram for adhesion dynamics of deformable capsules under shear flow. Soft Matt. 12 (33), 6918–6925.Google Scholar
Mackay, F. E., Ollila, S. T. & Denniston, C. 2013 Hydrodynamic forces implemented into LAMMPS through a lattice-Boltzmann fluid. Comput. Phys. Commun. 184 (8), 2021–2031.Google Scholar
MacMeccan, R. M., Clausen, J. R., Neitzel, G. P. & Aidun, C. K. 2009 Simulating deformable particle suspensions using a coupled lattice-Boltzmann and finite-element method. J. Fluid Mech. 618, 13.Google Scholar
Marth, W., Aland, S. & Voigt, A. 2016 Margination of white blood cells: a computational approach by a hydrodynamic phase field model. J. Fluid Mech. 790, 389–406.Google Scholar
Melchionna, S., Bernaschi, M., Succi, S., Kaxiras, E., Rybicki, F. J., Mitsouras, D., Coskun, A. U. & Feldman, C. L. 2010 Hydrokinetic approach to large-scale cardiovascular blood flow. Comput. Phys. Commun. 181 (3), 462–472.Google Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261.Google Scholar
Müller, K., Fedosov, D. A. & Gompper, G. 2014 Margination of micro- and nano-particles in blood flow and its effect on drug delivery. Sci. Rep. 4, 4871.Google Scholar
Müller, K., Fedosov, D. A. & Gompper, G. 2016 Understanding particle margination in blood flow – a step toward optimized drug delivery systems. Med. Engng Phys. 38 (1), 2–10.Google Scholar
Ndri, N. A., Shyy, W. & Tran-Son-Tay, R. 2003 Computational modeling of cell adhesion and movement using a continuum-kinetics approach. Biophys. J. 85 (4), 2273–2286.Google Scholar
Neri, D. & Bicknell, R. 2005 Tumour vascular targeting. Nat. Rev. Cancer 5 (6), 436.Google Scholar
Nix, S., Imai, Y., Matsunaga, D., Yamaguchi, T. & Ishikawa, T. 2014 Lateral migration of a spherical capsule near a plane wall in Stokes flow. Phys. Rev. E 90 (4), 043009.Google Scholar
Olla, P. 1997a The lift on a tank-treading ellipsoidal cell in a shear flow. J. Phys. II 7 (10), 1533–1540.Google Scholar
Olla, P. 1997b The role of tank-treading motions in the transverse migration of a spheroidal vesicle in a shear flow. J. Phys. A 30 (1), 317.Google Scholar
Ollila, S. T., Denniston, C., Karttunen, M. & Ala-Nissila, T. 2011 Fluctuating lattice-Boltzmann model for complex fluids. J. Chem. Phys. 134 (6), 064902.Google Scholar
Persson, P.-O.2005 Mesh generation for implicit geometries. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Persson, P.-O. & Strang, G. 2004 A simple mesh generator in MATLAB. SIAM Rev. 46 (2), 329–345.Google Scholar
Peskin, C. S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.Google Scholar
Plimpton, S. 1995 Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117 (1), 1–19.Google Scholar
Poiseuille, J. L. M. 1836 Recherches sur les causes du mouvement du sang dans les vaisseaux capillaires. Ann. Sci. Nat. 5, 111–115.Google Scholar
Pries, A. R., Neuhaus, D. & Gaehtgens, P. 1992 Blood viscosity in tube flow: dependence on diameter and hematocrit. Amer. J. Physiol. Heart Circ. Physiol. 263 (6), H1770–H1778.Google Scholar
Pries, A. R., Secomb, T. W., Gessner, T., Sperandio, M. B., Gross, J. F. & Gaehtgens, P. 1994 Resistance to blood flow in microvessels in vivo . Circ. Res. 75 (5), 904–915.Google Scholar
Qi, Q. M. & Shaqfeh, E. S. G. 2017 Theory to predict particle migration and margination in the pressure-driven channel flow of blood. Phys. Rev. Fluids 2 (9), 093102.Google Scholar
Ramakrishnan, N., Wang, Y., Eckmann, D. M., Ayyaswamy, P. S. & Radhakrishnan, R. 2017 Motion of a nano-spheroid in a cylindrical vessel flow: Brownian and hydrodynamic interactions. J. Fluid Mech. 821, 117–152.Google Scholar
Rivera, R. G. H., Zhang, X. & Graham, M. D. 2016 Mechanistic theory of margination and flow-induced segregation in confined multicomponent suspensions: simple shear and Poiseuille flows. Phys. Rev. Fluids 1 (6), 060501.Google Scholar
Schnitzer, J. E. 1998 Vascular targeting as a strategy for cancer therapy. New Engl. J. Med. 339 (7), 472–474.Google Scholar
Secomb, T. W., Styp-Rekowska, B. & Pries, A. R. 2007 Two-dimensional simulation of red blood cell deformation and lateral migration in microvessels. Ann. Biomed. Engng 35 (5), 755–765.Google Scholar
Seifert, U. 1999 Hydrodynamic lift on bound vesicles. Phys. Rev. Lett. 83 (4), 876.Google Scholar
Shen, Z., Ye, H., Kröger, M. & Li, Y. 2018 Aggregation of polyethylene glycol polymers suppresses receptor-mediated endocytosis of pegylated liposomes. Nanoscale 10 (9), 4545–4560.Google Scholar
Singh, R. K., Li, X. & Sarkar, K. 2014 Lateral migration of a capsule in plane shear near a wall. J. Fluid Mech. 739, 421–443.Google Scholar
Singh, R. K. & Sarkar, K. 2015 Hydrodynamic interactions between pairs of capsules and drops in a simple shear: effects of viscosity ratio and heterogeneous collision. Phys. Rev. E 92 (6), 063029.Google Scholar
Sinha, K. & Graham, M. D. 2016 Shape-mediated margination and demargination in flowing multicomponent suspensions of deformable capsules. Soft Matt. 12 (6), 1683–1700.Google Scholar
Smart, J. R. & Leighton, D. T. Jr. 1991 Measurement of the drift of a droplet due to the presence of a plane. Phys. Fluids A 3 (1), 21–28.Google Scholar
Sukumaran, S. & Seifert, U. 2001 Influence of shear flow on vesicles near a wall: a numerical study. Phys. Rev. E 64 (1), 011916.Google Scholar
Tan, J., Thomas, A. & Liu, Y. 2012 Influence of red blood cells on nanoparticle targeted delivery in microcirculation. Soft Matt. 8 (6), 1934–1946.Google Scholar
Tasciotti, E., Liu, X., Bhavane, R., Plant, K., Leonard, A. D., Price, B. K., Cheng, M. M.-C., Decuzzi, P., Tour, J. M., Robertson, F. et al. 2008 Mesoporous silicon particles as a multistage delivery system for imaging and therapeutic applications. Nat. Nanotechnol. 3 (3), 151.Google Scholar
Vahidkhah, K. & Bagchi, P. 2015 Microparticle shape effects on margination, near-wall dynamics and adhesion in a three-dimensional simulation of red blood cell suspension. Soft Matt. 11 (11), 2097–2109.Google Scholar
Vlahovska, P. M. & Gracia, R. S. 2007 Dynamics of a viscous vesicle in linear flows. Phys. Rev. E 75 (1), 016313.Google Scholar
Wootton, D. M. & Ku, D. N. 1999 Fluid mechanics of vascular systems, diseases, and thrombosis. Annu. Rev. Biomed. Engng 1 (1), 299–329.Google Scholar
Ye, H., Shen, Z. & Li, Y. 2018a Cell stiffness governs its adhesion dynamics on substrate under shear flow. IEEE Trans. Nanotechnol. 17 (3), 407–411.Google Scholar
Ye, H., Shen, Z. & Li, Y. 2018b Computational modeling of magnetic particle margination within blood flow through LAMMPS. Comput. Mech. 62 (3), 457–476.Google Scholar
Ye, H., Shen, Z., Yu, L., Wei, M. & Li, Y. 2017a Anomalous vascular dynamics of nanoworms within blood flow. ACS Biomater. Sci. Engng 4 (1), 66–77.Google Scholar
Ye, H., Shen, Z., Yu, L., Wei, M. & Li, Y. 2018c Manipulating nanoparticle transport within blood flow through external forces: an exemplar of mechanics in nanomedicine. Proc. R. Soc. Lond. A 474 (2211), 20170845.Google Scholar
Ye, H., Wei, H., Huang, H. & Lu, X.-Y. 2017b Two tandem flexible loops in a viscous flow. Phys. Fluids 29 (2), 021902.Google Scholar
Zhang, J., Johnson, P. C. & Popel, A. S. 2007 An immersed boundary lattice Boltzmann approach to simulate deformable liquid capsules and its application to microscopic blood flows. Phys. Biol. 4 (4), 285.Google Scholar
Zhang, J., Johnson, P. C. & Popel, A. S. 2008 Red blood cell aggregation and dissociation in shear flows simulated by lattice Boltzmann method. J. Biomech. 41 (1), 47–55.Google Scholar
Zhao, H. & Shaqfeh, E. S. G. 2011 Shear-induced platelet margination in a microchannel. Phys. Rev. E 83 (6), 061924.Google Scholar
Zhao, H. & Shaqfeh, E. S. G. 2013 The dynamics of a non-dilute vesicle suspension in a simple shear flow. J. Fluid Mech. 725, 709–731.Google Scholar
Zhao, H., Shaqfeh, E. S. G. & Narsimhan, V. 2012 Shear-induced particle migration and margination in a cellular suspension. Phys. Fluids 24 (1), 011902.Google Scholar
Zhao, H., Spann, A. P. & Shaqfeh, E. S. G. 2011 The dynamics of a vesicle in a wall-bound shear flow. Phys. Fluids 23 (12), 121901.Google Scholar
Supplementary material: File

Ye et al. supplementary material

Ye et al. supplementary material 1

Download Ye et al. supplementary material(File)
File 1.8 MB