Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-19T13:22:02.356Z Has data issue: false hasContentIssue false
  • English
  • Français

Investigations of non-hydrostatic, stably stratified and rapidly rotating flows

Published online by Cambridge University Press:  25 July 2016

David Nieves ,
Ian Grooms ,
Keith Julien  and
Jeffrey B. Weiss
David Nieves*
Affiliation:
Department of Applied Mathematics, University of Colorado, Boulder, CO 80309, USA
Ian Grooms
Affiliation:
Department of Applied Mathematics, University of Colorado, Boulder, CO 80309, USA
Keith Julien
Affiliation:
Department of Applied Mathematics, University of Colorado, Boulder, CO 80309, USA
Jeffrey B. Weiss
Affiliation:
Department of Atmospheric and Oceanic Sciences, University of Colorado, Boulder, CO 80309, USA
*
†Email address for correspondence: david.nieves@colorado.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an investigation of rapidly rotating (small Rossby number 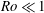$Ro\ll 1$) stratified turbulence where the stratification strength is varied from weak (large Froude number 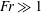$Fr\gg 1$) to strong (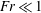$Fr\ll 1$). The investigation is set in the context of a reduced model derived from the Boussinesq equations that retains anisotropic inertia-gravity waves with order-one frequencies and highlights a regime of wave–eddy interactions. Numerical simulations of the reduced model are performed where energy is injected by a stochastic forcing of vertical velocity, which forces wave modes only. The simulations reveal two regimes: characterized by the presence of well-formed, persistent and thin turbulent layers of locally weakened stratification at small Froude numbers, and by the absence of layers at large Froude numbers. Both regimes are characterized by a large-scale barotropic dipole enclosed by small-scale turbulence. When the Reynolds number is not too large, a direct cascade of barotropic kinetic energy is observed, leading to total energy equilibration. We examine net energy exchanges that occur through vortex stretching and vertical buoyancy flux and diagnose the horizontal scales active in these exchanges. We find that the baroclinic motions inject energy directly to the largest scales of the barotropic mode, implying that the large-scale barotropic dipole is not the end result of an inverse cascade within the barotropic mode.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , pp. 430 - 458
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aluie, H. & Kurien, S. 2011 Joint downscale fluxes of energy and potential enstrophy in rotating stratified boussinesq flows. Europhys. Lett. 96 (4), 44006.CrossRefGoogle Scholar
Balmforth, N. J., Smith, S. G. L. & Young, W. R. 1998 Dynamics of interfaces and layers in a stratified turbulent fluid. J. Fluid Mech. 355, 329–358.CrossRefGoogle Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52 (24), 4410–4428.2.0.CO;2>CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2000 Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 418, 167–188.CrossRefGoogle Scholar
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451.CrossRefGoogle Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
Cambon, C. 2001 Turbulence and vortex structures in rotating and stratified flows. Eur. J. Mech. (B/Fluids) 20 (4), 489–510.CrossRefGoogle Scholar
Charney, J. G. 1948 On the scale of atmospheric motions. Geophys. Publ. 17, 1–17.Google Scholar
Charney, J. G. 1971 Geostrophic turbulence. J. Atmos. Sci. 28 (6), 1087–1095.2.0.CO;2>CrossRefGoogle Scholar
Dritschel, D.G. & McIntyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of Eddy-transport barriers. J. Atmos. Sci. 65 (3), 855–874.CrossRefGoogle Scholar
Eady, E. T. 1949 Long waves and cyclone waves. Tellus 1 (3), 33–52.CrossRefGoogle Scholar
Embid, P. F. & Majda, A. J. 1996 Averaging over fast gravity waves for geophysical flows with arbitrary potential vorticity. Commun. Part. Diff. Equ. 21, 619–658.CrossRefGoogle Scholar
Embid, P. F. & Majda, A. J. 1998 Low Froude number limiting dynamics for stably stratified flow with small or finite Rossby numbers. Geophys. Astrophys. Fluid Dyn. 87 (1–2), 1–50.CrossRefGoogle Scholar
Emery, W. J., Lee, W. G. & Magaard, L. 1984 Geographic and seasonal distributions of Brunt–Väisälä frequency and Rossby radii in the North Pacific and North Atlantic. J. Phys. Oceanogr. 14 (2), 294–317.2.0.CO;2>CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
van Haren, H. & Millot, C. 2005 Gyroscopic waves in the Mediterranean Sea. Geophys. Res. Lett. 32 (24), l24614.CrossRefGoogle Scholar
Higham, D. J. 2001 An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43 (3), 525–546.CrossRefGoogle Scholar
Julien, K. & Knobloch, E. 2007 Reduced models for fluid flows with strong constraints. J. Math. Phys. 48, 065405.CrossRefGoogle Scholar
Julien, K., Knobloch, E., Milliff, R. & Werne, J. 2006 Generalized quasi-geostrophy for spatially anisotropic rotationally constrained flows. J. Fluid Mech. 555, 233–274.CrossRefGoogle Scholar
Julien, K., Knobloch, E. & Werne, J. 1998 A new class of equations for rotationally constrained flows. Theor. Comput. Fluid Dyn. 11, 251–261.CrossRefGoogle Scholar
Kimura, Y. & Herring, J. R. 2012 Energy spectra of stably stratified turbulence. J. Fluid Mech. 698, 19–50.CrossRefGoogle Scholar
Larichev, V. D. & Held, I. M. 1995 Eddy amplitudes and fluxes in a homogeneous model of fully developed baroclinic instability. J. Phys. Oceanogr. 25 (10), 2285–2297.2.0.CO;2>CrossRefGoogle Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.CrossRefGoogle Scholar
Lorenz, E. N. 1955 Available potential energy and the maintenance of the general circulation. Tellus 7 (2), 157–167.CrossRefGoogle Scholar
Majda, A. J. & Embid, P. F. 1998 Averaging over fast gravity waves for geophysical flows with unbalanced initial data. Theor. Comput. Fluid Dyn. 11, 155–169.CrossRefGoogle Scholar
Marino, R., Mininni, P. D., Rosenberg, D. & Pouquet, A. 2013 Inverse cascades in rotating stratified turbulence: fast growth of large scales. Europhys. Lett. 102 (4), 44006.CrossRefGoogle Scholar
Miesch, M. S. 2005 Large-scale dynamics of the convection zone and tachocline. Living Rev. Solar Phys. 2, 1.CrossRefGoogle Scholar
Mininni, P. D., Rosenberg, D. & Pouquet, A. 2012 Isotropization at small scales of rotating helically driven turbulence. J. Fluid Mech. 699, 263–279.CrossRefGoogle Scholar
Ozmidov, R. V. 1965 On the turbulent exchange in a stably stratified ocean. Atmos. Ocean. Phys. 1, 861–871.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.CrossRefGoogle Scholar
Phillips, O. M. 1972 Turbulence in a strongly stratified fluid is it unstable? Deep-Sea Res. Oceanogr. Abstracts 19 (1), 79–81.CrossRefGoogle Scholar
Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. 2012 Thermal and electrical conductivity of iron at Earth/’s core conditions. Nature 485 (7398), 355–358.CrossRefGoogle ScholarPubMed
Proudman, J. 1916 On the motion of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. A 92 (642), 408–424.Google Scholar
Rocha, C. B., Young, W. R. & Grooms, I. 2016 On Galerkin approximations of the surface active quasigeostrophic equations. J. Phys. Oceanogr. 46 (1), 125–139.CrossRefGoogle Scholar
Rubio, A. M., Julien, K., Knobloch, E. & Weiss, J. B. 2014 Upscale energy transfer in three-dimensional rapidly rotating turbulent convection. Phys. Rev. Lett. 112, 144501.CrossRefGoogle ScholarPubMed
Sen, A., Mininni, P. D., Rosenberg, D. & Pouquet, A. 2012 Anisotropy and nonuniversality in scaling laws of the large-scale energy spectrum in rotating turbulence. Phys. Rev. E 86 (3), 036319.CrossRefGoogle ScholarPubMed
Smith, K. S. & Vallis, G. K. 2001 The scales and equilibration of midocean eddies: freely evolving flow. J. Phys. Oceanogr. 31 (2), 554–571.2.0.CO;2>CrossRefGoogle Scholar
Smith, K. S. & Vallis, G. K. 2002 The scales and equilibration of midocean eddies: forced-dissipative flow. J. Phys. Oceanogr. 32 (6), 1699–1720.2.0.CO;2>CrossRefGoogle Scholar
Smith, L. M. & Lee, Y. 2005 On near resonances and symmetry breaking in forced rotating flows at moderate Rossby number. J. Fluid Mech. 535, 111–142.CrossRefGoogle Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11, 1608–1622.CrossRefGoogle Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.CrossRefGoogle Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96 (2), 297–324.CrossRefGoogle Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.CrossRefGoogle Scholar
Stellmach, S., Traxler, A., Garaud, P., Brummell, N. & Radko, T. 2011 Dynamics of fingering convection. Part 2. The formation of thermohaline staircases. J. Fluid Mech. 677, 554–571.CrossRefGoogle Scholar
Sukhatme, J. & Smith, L. M. 2008 Vortical and wave modes in 3D rotating stratified flows: random large-scale forcing. Geophys. Astrophys. Fluid Dyn. 102 (5), 437–455.CrossRefGoogle Scholar
Taylor, G. I. 1923 Experiments on the motion of solid bodies in rotating fluids. Proc. R. Soc. Lond. A 104 (725), 213–218.Google Scholar
Temam, R. & Wirosoetisno, D. 2010 Stability of the slow manifold in the primitive equations. SIAM J. Math. Anal. 42, 427–458.CrossRefGoogle Scholar
Temam, R. & Wirosoetisno, D. 2011 Slow manifolds and invariant sets of the primitive equations. J. Atmos. Sci. 68, 675–682.CrossRefGoogle Scholar
Timmermans, M.-L., Garrett, C. & Carmack, E. 2003 The thermohaline structure and evolution of the deep waters in the Canada Basin, Arctic Ocean. Deep-Sea Res. I 50 (10), 1305–1321.CrossRefGoogle Scholar
Timmermans, M.-L., Melling, H. & Rainville, L. 2007 Dynamics in the deep Canada basin, arctic ocean, inferred by thermistor chain time series. J. Phys. Oceanogr. 37 (4), 1066–1076.CrossRefGoogle Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.CrossRefGoogle Scholar
Waite, M. L. & Bartello, P. 2006 The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.CrossRefGoogle Scholar
Whitehead, J. P. & Wingate, B. A. 2014 The influence of fast waves and fluctuations on the evolution of the dynamics on the slow manifold. J. Fluid Mech. 757, 155–178.CrossRefGoogle Scholar
Wingate, B. A., Embid, P., Holmes-Cerfon, M. & Taylor, M. A. 2011 Low Rossby limiting dynamics for stably stratified flow with finite Froude number. J. Fluid Mech. 676, 546–571.CrossRefGoogle Scholar
Zeman, O. 1994 A note on the spectra and decay of rotating homogeneous turbulence. Phys. Fluids 6 (10), 3221–3223.CrossRefGoogle Scholar