Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T18:00:04.385Z Has data issue: false hasContentIssue false
  • English
  • Français

The large-scale flow structure in turbulent rotating Rayleigh–Bénard convection

Published online by Cambridge University Press:  01 November 2011

Stephan Weiss  and
Guenter Ahlers
Stephan Weiss
Affiliation:
Department of Physics, University of California, Santa Barbara, CA 93106, USA
Guenter Ahlers*
Affiliation:
Department of Physics, University of California, Santa Barbara, CA 93106, USA
*
†Email address for correspondence: guenter@physics.ucsb.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

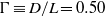We report on the influence of rotation about a vertical axis on the large-scale circulation (LSC) of turbulent Rayleigh–Bénard convection in a cylindrical vessel with aspect ratio (where 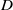is the diameter and 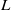the height of the sample). The working fluid is water at an average temperature 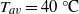with a Prandtl number 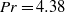. For rotation rates 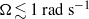, corresponding to inverse Rossby numbers 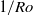between 0 and 20, we investigated the temperature distribution at the sidewall and from it deduced properties of the LSC. The work covered the Rayleigh-number range 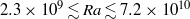. We measured the vertical sidewall temperature gradient, the dynamics of the LSC and flow-mode transitions from single-roll states (SRSs) to double-roll states (DRSs). We found that modest rotation stabilizes the SRSs. For modest 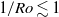we found the unexpected result that the vertical LSC plane rotated in the prograde direction (i.e. faster than the sample chamber), with the rotation at the horizontal midplane faster than near the top and bottom. This differential rotation led to disruptive events called half-turns, where the plane of the top or bottom section of the LSC underwent a rotation through an angle of 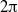relative to the main portion of the LSC. The signature of the LSC persisted even for large 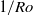where Ekman vortices are expected. We consider the possibility that this signature actually is generated by a two-vortex state rather than by a LSC. Whenever possible, we compare our results with those for a 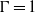sample by Zhong & Ahlers (J. Fluid Mech., vol. 665, 2010, pp. 300–333).

JFM classification

Convection: Convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 688 , 10 December 2011 , pp. 461 - 492
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ahlers, G. 2009 Turbulent convection. Physics 2, 74-1–7.CrossRefGoogle Scholar
2. Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–538.CrossRefGoogle Scholar
3. Bailon-Cuba, J., Emran, M. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.CrossRefGoogle Scholar
4. Brown, E. & Ahlers, G. 2006a Effect of the Earth’s Coriolis force on turbulent Rayleigh–Bénard convection in the laboratory. Phys. Fluids 18, 125108.CrossRefGoogle Scholar
5. Brown, E. & Ahlers, G. 2006b Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.CrossRefGoogle Scholar
6. Brown, E. & Ahlers, G. 2007 Temperature gradients, and search for non-Boussinesq effects, in the interior of turbulent Rayleigh–Bénard convection. Europhys. Lett. 80, 14001.CrossRefGoogle Scholar
7. Brown, E. & Ahlers, G. 2008a Azimuthal asymmetries of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20, 105105.Google Scholar
8. Brown, E. & Ahlers, G. 2008b A model of diffusion in a potential well for the dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20, 075101.Google Scholar
9. Brown, E. & Ahlers, G. 2009 The origin of oscillations of the large-scale circulation of turbulent Rayleigh–Bénard convection. J. Fluid Mech. 638, 383–400.CrossRefGoogle Scholar
10. Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.CrossRefGoogle ScholarPubMed
11. Ciliberto, S., Cioni, S. & Laroche, C. 1996 Large-scale flow properties of turbulent thermal convection. Phys. Rev. E 54, R5901–R5904.CrossRefGoogle ScholarPubMed
12. Du, Y. B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.CrossRefGoogle Scholar
13. Funfschilling, D. & Ahlers, G. 2004 Plume motion and large scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.CrossRefGoogle Scholar
14. Funfschilling, D., Brown, E. & Ahlers, G. 2008 Torsional oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 607, 119–139.CrossRefGoogle Scholar
15. Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.CrossRefGoogle Scholar
16. Hart, J. E., Kittelman, S. & Ohlsen, D. R. 2002 Mean flow precession and temperature probability density functions in turbulent rotating convection. Phys. Fluids 14, 955–962.CrossRefGoogle Scholar
17. Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.CrossRefGoogle Scholar
18. King, E., Stellmach, S., Noir, J., Hansen, U. & Aurnou, J. 2009 Boundary layer control of rotating convection systems. Nature 457, 301–304.CrossRefGoogle ScholarPubMed
19. Kunnen, R. P. J. 2008 Turbulent rotating convection. PhD thesis, University of Eindhoven.Google Scholar
20. Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2008 Breakdown of large-scale circulation in turbulent rotating convection. Europhys. Lett. 84, 24001.CrossRefGoogle Scholar
21. Kunnen, R. P. J., Geurts, B. J. & Clercx, H. J. H. 2010 Experimental and numerical investigation of turbulent convection in a rotating cylinder. J. Fluid Mech. 642, 445–476.CrossRefGoogle Scholar
22. Kunnen, R. P. J., Stevens, R. J. A. M., Overkamp, J., Sun, C., van Heijst, G. & Clercx, H. J. H. 2011 The role of Stewartson and Ekman layers in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 422–442.CrossRefGoogle Scholar
23. Liu, Y. & Ecke, R. 2009 Heat transport measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 80, 036314.CrossRefGoogle ScholarPubMed
24. Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
25. Malkus, M. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 185–195.Google Scholar
26. Nikolaenko, A., Brown, E., Funfschilling, D. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells with aspect ratio one and less. J. Fluid Mech. 523, 251–260.CrossRefGoogle Scholar
27. Rossby, H. T. 1969 A study of Bénard convection with and without rotation. J. Fluid Mech. 36, 309–335.CrossRefGoogle Scholar
28. Stevens, R., Clercx, H. J. H. & Lohse, D. 2011a Effect of plumes on measuring the large scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 23, 095110.CrossRefGoogle Scholar
29. Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010 Boundary layers in rotating weakly turbulent Rayleigh–Bénard convection. Phys. Fluids 22, 085103.CrossRefGoogle Scholar
30. Stevens, R. J. A. M., Overkamp, J., Lohse, D. & Clercx, H. J. H. 2011b Disappearance of aspect ratio dependence of heat transport with increasing rotation rate in turbulent Rayleigh–Bénard convection. Phys. Rev. E (in press).Google Scholar
31. Stevens, R. J. A. M., Zhong, J., Clercx, H. J. H., Ahlers, G. & Lohse, D. 2009 Transitions between turbulent states in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 024503.CrossRefGoogle ScholarPubMed
32. Sun, C., Ren, L.-Y., Song, H. & Xia, K.-Q. 2005a Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells of widely varying aspect ratios. J. Fluid Mech. 542, 165–174.CrossRefGoogle Scholar
33. Sun, C., Xi, H. D. & Xia, K. Q. 2005b Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.CrossRefGoogle Scholar
34. Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulence convection in water. Phys. Rev. E 47, R2253–R2256.CrossRefGoogle ScholarPubMed
35. Tritton, D. J. 1988 Physical Fluid Dynamics. Oxford University Press.Google Scholar
36. van der Poel, E., Stevens, R. J. A. M. & Lohse, D. 2011 Connecting flow structures and heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. E 84, 045303.CrossRefGoogle ScholarPubMed
37. Weiss, S. & Ahlers, G. 2011a Heat transport by turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. (in press).CrossRefGoogle Scholar
38. Weiss, S. & Ahlers, G. 2011b Turbulent Rayleigh–Bénard convection in a cylindrical container with aspect ration and Prandtl number Pr = 4.38. J. Fluid Mech. 676, 5–40.CrossRefGoogle Scholar
39. Weiss, S., Stevens, R., Zhong, J.-Q., Clercx, H., Lohse, D. & Ahlers, G. 2010 Finite-size effects lead to supercritical bifurcations in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 105, 225401.CrossRefGoogle ScholarPubMed
40. Xi, H.-D. & Xia, K.-Q. 2007 Cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75, 066307.CrossRefGoogle ScholarPubMed
41. Xi, H.-D. & Xia, K.-Q. 2008a Azimuthal motion, reorientation, cessation, and reversals of the large-scale circulation in turbulent thermal convection: a comparative study in aspect ratio oner and one-half geometries. Phys. Rev. E 78, 036326.CrossRefGoogle Scholar
42. Xi, H.-D. & Xia, K.-Q. 2008b Flow mode transition in turbulent thermal convection. Phys. Fluids 20, 055104.CrossRefGoogle Scholar
43. Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.CrossRefGoogle ScholarPubMed
44. Xia, K.-Q. & Lui, S.-L. 1997 Turbulent thermal convection with an obstructed sidewall. Phys. Rev. Lett. 79, 5006–5009.CrossRefGoogle Scholar
45. Xu, X., Bajaj, K. M. S. & Ahlers, G. 2000 Heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 84, 4357–4360.CrossRefGoogle ScholarPubMed
46. Zhong, J.-Q. & Ahlers, G. 2010 Heat transport and the large-scale circulation in rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 665, 300–333.CrossRefGoogle Scholar
47. Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.Google ScholarPubMed
48. Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.CrossRefGoogle Scholar
Supplementary material: PDF

Weiss and Ahlers supplementary material

Supplement

Download Weiss and Ahlers supplementary material(PDF)
PDF 557.3 KB