Article contents
Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers
Published online by Cambridge University Press: 14 October 2015
Abstract
In this study, a CFD-based linear dynamics model combined with the direct Computational Fluid Dynamics/Computational Structural Dynamics (CFD/CSD) simulation method is utilized to study the physical mechanisms underlying frequency lock-in in vortex-induced vibrations (VIVs). An identification method is employed to construct the reduced-order models (ROMs) of unsteady aerodynamics for the incompressible flow past a vibrating cylinder at low Reynolds numbers (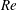 $Re$). Reduced-order-model-based fluid–structure interaction models for VIV are also constructed by coupling ROMs and structural motion equations. The effects of the natural frequency of the cylinder, mass ratio and structural damping coefficient on the dynamics of the coupled system at
$Re$). Reduced-order-model-based fluid–structure interaction models for VIV are also constructed by coupling ROMs and structural motion equations. The effects of the natural frequency of the cylinder, mass ratio and structural damping coefficient on the dynamics of the coupled system at 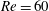 $Re=60$ are investigated. The results show that the frequency lock-in phenomenon at low Reynolds numbers can be divided into two patterns according to different induced mechanisms. The two patterns are ‘resonance-induced lock-in’ and ‘flutter-induced lock-in’. When the natural frequency of the cylinder is in the vicinity of the eigenfrequency of the uncoupled wake mode (WM), only the WM is unstable. The dynamics of the coupled system is dominated by resonance. Meanwhile, for relatively high natural frequencies (i.e. greater than the eigenfrequency of the uncoupled WM), the structure mode becomes unstable, and the coupling between the two unstable modes eventually leads to flutter. Flutter is the root cause of frequency lock-in and the higher vibration amplitude of the cylinder than that of the resonance region. This result provides evidence for the finding of De Langre (J. Fluids Struct., vol. 22, 2006, pp. 783–791) that frequency lock-in is caused by coupled-mode flutter. The linear model exactly predicts the onset reduced velocity of frequency lock-in compared with that of direct numerical simulations. In addition, the transition frequency predicted by the linear model is in close coincidence with the amplitude of the lift coefficient of a fixed cylinder for high mass ratios. Therefore, it confirms that linear models can capture a significant part of the inherent physics of the frequency lock-in phenomenon.
$Re=60$ are investigated. The results show that the frequency lock-in phenomenon at low Reynolds numbers can be divided into two patterns according to different induced mechanisms. The two patterns are ‘resonance-induced lock-in’ and ‘flutter-induced lock-in’. When the natural frequency of the cylinder is in the vicinity of the eigenfrequency of the uncoupled wake mode (WM), only the WM is unstable. The dynamics of the coupled system is dominated by resonance. Meanwhile, for relatively high natural frequencies (i.e. greater than the eigenfrequency of the uncoupled WM), the structure mode becomes unstable, and the coupling between the two unstable modes eventually leads to flutter. Flutter is the root cause of frequency lock-in and the higher vibration amplitude of the cylinder than that of the resonance region. This result provides evidence for the finding of De Langre (J. Fluids Struct., vol. 22, 2006, pp. 783–791) that frequency lock-in is caused by coupled-mode flutter. The linear model exactly predicts the onset reduced velocity of frequency lock-in compared with that of direct numerical simulations. In addition, the transition frequency predicted by the linear model is in close coincidence with the amplitude of the lift coefficient of a fixed cylinder for high mass ratios. Therefore, it confirms that linear models can capture a significant part of the inherent physics of the frequency lock-in phenomenon.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 174
- Cited by



