Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-07T14:31:32.529Z Has data issue: false hasContentIssue false
  • English
  • Français

Migration of confined micro-swimmers subject to anisotropic diffusion

Published online by Cambridge University Press:  29 April 2024

Mingyang Guan Open the ORCID record for Mingyang Guan [Opens in a new window] ,
Weiquan Jiang Open the ORCID record for Weiquan Jiang [Opens in a new window] ,
Luoyi Tao ,
Guoqian Chen Open the ORCID record for Guoqian Chen [Opens in a new window]  and
Joseph H.W. Lee
Mingyang Guan
Affiliation:
Laboratory of Systems Ecology and Sustainability Science, College of Engineering, Peking University, Beijing 100871, PR China
Weiquan Jiang
Affiliation:
Macao Environmental Research Institute, Macau University of Science and Technology, Macao 999078, PR China
Luoyi Tao
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Madras, Chennai 600036, India
Guoqian Chen*
Affiliation:
Laboratory of Systems Ecology and Sustainability Science, College of Engineering, Peking University, Beijing 100871, PR China Macao Environmental Research Institute, Macau University of Science and Technology, Macao 999078, PR China
Joseph H.W. Lee*
Affiliation:
Macao Environmental Research Institute, Macau University of Science and Technology, Macao 999078, PR China
*
†Email addresses for correspondence: gqchen@pku.edu.cn, jhwlee@must.edu.mo
†Email addresses for correspondence: gqchen@pku.edu.cn, jhwlee@must.edu.mo
Get access Rights & Permissions [Opens in a new window]

Abstract

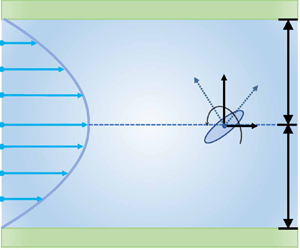
Shear-induced migration of elongated micro-swimmers exhibiting anisotropic Brownian diffusion at a population scale is investigated analytically in this work. We analyse the steady motion of confined ellipsoidal micro-swimmers subject to coupled diffusion in a general setting within a continuum homogenisation framework, as an extension of existing studies on macro-transport processes, by allowing for the direct coupling of convection and diffusion in local and global spaces. The analytical solutions are validated successfully by comparison with numerical results from Monte Carlo simulations. Subsequently, we demonstrate from the probability perspective that symmetric actuation does not yield net vertical polarisation in a horizontal flow, unless non-spherical shapes, external fields or direct coupling effects are harnessed to generate steady locomotion. Coupled diffusivities modify remarkably the drift velocity and vertical migration of motile micro-swimmers exposed to fluid shear. The interplay between stochastic swimming and preferential alignment could explain the diverse concentration and orientation distributions, including rheological formations of depletion layers, centreline focusing and surface accumulation. Results of the analytical study shed light on unravelling peculiar self-propulsion strategies and dispersion dynamics in active-matter systems, with implications for various transport problems arising from the fluctuating shape, size and other external or inter-particle interactions of swimmers in confined environments.

JFM classification

Biological Fluid Dynamics: Swimming/flying Mass Transport: Dispersion
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 985 , 25 April 2024 , A44
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barry, M.T., Rusconi, R., Guasto, J.S. & Stocker, R. 2015 Shear-induced orientational dynamics and spatial heterogeneity in suspensions of motile phytoplankton. J. R. Soc. Interface 12 (112), 20150791.CrossRefGoogle Scholar
Barton, N.G. 1983 On the method of moments for solute dispersion. J. Fluid Mech. 126, 205–218.CrossRefGoogle Scholar
Bearon, R.N. & Hazel, A.L. 2015 The trapping in high-shear regions of slender bacteria undergoing chemotaxis in a channel. J. Fluid Mech. 771, R3.CrossRefGoogle Scholar
Bearon, R.N., Hazel, A.L. & Thorn, G.J. 2011 The spatial distribution of gyrotactic swimming micro-organisms in laminar flow fields. J. Fluid Mech. 680, 602–635.CrossRefGoogle Scholar
Berke, A.P., Turner, L., Berg, H.C. & Lauga, E. 2008 Hydrodynamic attraction of swimming microorganisms by surfaces. Phys. Rev. Lett. 101 (3), 038102.CrossRefGoogle ScholarPubMed
Brenner, H. 1967 Coupling between the translational and rotational Brownian motions of rigid particles of arbitrary shape: II. General theory. J. Colloid Interface Sci. 23 (3), 407–436.CrossRefGoogle Scholar
Brenner, H. & Edwards, D. 1993 Macrotransport Processes. Butterworth-Heinemann.Google Scholar
Brumley, D.R., Polin, M., Pedley, T.J. & Goldstein, R.E. 2015 Metachronal waves in the flagellar beating of Volvox and their hydrodynamic origin. J. R. Soc. Interface 12 (108), 20141358.CrossRefGoogle Scholar
Cates, M.E. & Tjhung, E. 2018 Theories of binary fluid mixtures: from phase-separation kinetics to active emulsions. J. Fluid Mech. 836, P1.CrossRefGoogle Scholar
Chen, G., Perazzo, A. & Stone, H.A. 2020 Influence of salt on the viscosity of polyelectrolyte solutions. Phys. Rev. Lett. 124 (17), 177801.CrossRefGoogle ScholarPubMed
Choudhary, A., Nambiar, S. & Stark, H. 2023 Orientational dynamics and rheology of active suspensions in weakly viscoelastic flows. Commun. Phys. 6 (1), 1–11.CrossRefGoogle Scholar
Debnath, S., Jiang, W., Guan, M. & Chen, G. 2022 Effect of ring-source release on dispersion process in Poiseuille flow with wall absorption. Phys. Fluids 34 (2), 027106.CrossRefGoogle Scholar
Durham, W.M. & Stocker, R. 2012 Thin phytoplankton layers: characteristics, mechanisms, and consequences. Annu. Rev. Mar. Sci. 4 (1), 177–207.CrossRefGoogle Scholar
Ezhilan, B. & Saintillan, D. 2015 Transport of a dilute active suspension in pressure-driven channel flow. J. Fluid Mech. 777, 482–522.CrossRefGoogle Scholar
Fung, L. 2023 Analogy between streamers in sinking spheroids, gyrotactic plumes and chemotactic collapse. J. Fluid Mech. 961, A12.CrossRefGoogle Scholar
Gouiller, C., Raynal, F., Maquet, L., Bourgoin, M., Cottin-Bizonne, C., Volk, R. & Ybert, C. 2021 Mixing and unmixing induced by active camphor particles. Phys. Rev. Fluids 6 (1), 014501.CrossRefGoogle Scholar
Guan, M. & Chen, G. 2024 Streamwise dispersion of soluble matter in solvent flowing through a tube. J. Fluid Mech. 980, A33.CrossRefGoogle Scholar
Guan, M., Jiang, W., Wang, B., Zeng, L., Li, Z. & Chen, G. 2023 Pre-asymptotic dispersion of active particles through a vertical pipe: the origin of hydrodynamic focusing. J. Fluid Mech. 962, A14.CrossRefGoogle Scholar
Guan, M., Zeng, L., Jiang, W., Guo, X., Wang, P., Wu, Z., Li, Z. & Chen, G. 2022 Effects of wind on transient dispersion of active particles in a free-surface wetland flow. Commun. Nonlinear Sci. Numer. Simul. 115, 106766.CrossRefGoogle Scholar
Guan, M., Zeng, L., Li, C., Guo, X., Wu, Y. & Wang, P. 2021 Transport model of active particles in a tidal wetland flow. J. Hydrol. 593, 125812.CrossRefGoogle Scholar
Hill, J., Kalkanci, O., McMurry, J.L. & Koser, H. 2007 Hydrodynamic surface interactions enable Escherichia coli to seek efficient routes to swim upstream. Phys. Rev. Lett. 98 (6), 068101.CrossRefGoogle ScholarPubMed
Hill, N.A. & Bees, M.A. 2002 Taylor dispersion of gyrotactic swimming micro-organisms in a linear flow. Phys. Fluids 14 (8), 2598–2605.CrossRefGoogle Scholar
Hwang, Y. & Pedley, T.J. 2014 Bioconvection under uniform shear: linear stability analysis. J. Fluid Mech. 738, 522–562.CrossRefGoogle Scholar
Ishikawa, T. & Pedley, T.J. 2014 Dispersion of model microorganisms swimming in a nonuniform suspension. Phys. Rev. E 90 (3), 033008.CrossRefGoogle Scholar
Jakuszeit, T., Croze, O.A. & Bell, S. 2019 Diffusion of active particles in a complex environment: role of surface scattering. Phys. Rev. E 99 (1), 012610.CrossRefGoogle Scholar
Jeffery, G.B. & Filon, L. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102 (715), 161–179.Google Scholar
Jiang, W. & Chen, G. 2019 Dispersion of active particles in confined unidirectional flows. J. Fluid Mech. 877, 1–34.CrossRefGoogle Scholar
Jiang, W. & Chen, G. 2020 Dispersion of gyrotactic micro-organisms in pipe flows. J. Fluid Mech. 889, A18.CrossRefGoogle Scholar
Jiang, W. & Chen, G. 2021 Transient dispersion process of active particles. J. Fluid Mech. 927, A11.CrossRefGoogle Scholar
Kamal, C. & Lauga, E. 2023 Resistive-force theory of slender bodies in viscosity gradients. J. Fluid Mech. 963, A24.CrossRefGoogle Scholar
Karrila, S.J. & Kim, S. 1991 Microhydrodynamics: principles and selected applications. In Microhydrodynamics (ed. S. Kim & S.J. Karrila). Butterworth-Heinemann.Google Scholar
Kaya, T. & Koser, H. 2009 Characterization of hydrodynamic surface interactions of Escherichia coli cell bodies in shear flow. Phys. Rev. Lett. 103 (13), 138103.CrossRefGoogle ScholarPubMed
Khair, A.S. 2022 Taylor dispersion of elongated rods at small and large rotational Péclet numbers. Phys. Rev. Fluids 7 (1), 014502.CrossRefGoogle Scholar
Kumar, A.H., Thomson, S.J., Powers, T.R. & Harris, D.M. 2021 Taylor dispersion of elongated rods. Phys. Rev. Fluids 6 (9), 094501.CrossRefGoogle Scholar
Lauga, E. 2011 Life around the scallop theorem. Soft Matt. 7 (7), 3060–3065.CrossRefGoogle Scholar
Lauga, E. 2020 The Fluid Dynamics of Cell Motility. Cambridge University Press.CrossRefGoogle Scholar
Leal, L.G. & Hinch, E.J. 1972 The rheology of a suspension of nearly spherical particles subject to Brownian rotations. J. Fluid Mech. 55 (4), 745–765.CrossRefGoogle Scholar
Li, G. & Tang, J.X. 2009 Accumulation of microswimmers near a surface mediated by collision and rotational Brownian motion. Phys. Rev. Lett. 103 (7), 078101.CrossRefGoogle Scholar
Liao, W., Erben, E., Kreysing, M. & Lauga, E. 2023 Theoretical model of confined thermoviscous flows for artificial cytoplasmic streaming. Phys. Rev. Fluids 8 (3), 034202.CrossRefGoogle Scholar
Manela, A. & Frankel, I. 2003 Generalized Taylor dispersion in suspensions of gyrotactic swimming micro-organisms. J. Fluid Mech. 490, 99–127.CrossRefGoogle Scholar
Marchetti, M.C., Joanny, J.F., Ramaswamy, S., Liverpool, T.B., Prost, J., Rao, M. & Simha, R.A. 2013 Hydrodynamics of soft active matter. Rev. Mod. Phys. 85 (3), 1143–1189.CrossRefGoogle Scholar
Mei, C.C., Auriault, J.L. & Ng, C.-O. 1996 Some applications of the homogenization theory. In Advances in Applied Mechanics (ed. J.W. Hutchinson & T.Y. Wu), vol. 32, pp. 277–348. Elsevier.CrossRefGoogle Scholar
Morris, J.F. 2020 Shear thickening of concentrated suspensions: recent developments and relation to other phenomena. Annu. Rev. Fluid Mech. 52 (1), 121–144.CrossRefGoogle Scholar
Morris, J.F. & Brady, J.F. 1996 Self-diffusion in sheared suspensions. J. Fluid Mech. 312, 223–252.CrossRefGoogle Scholar
Ng, C.-O. 2006 a Dispersion in open-channel flow subject to the processes of sorptive exchange on the bottom and air–water exchange on the free surface. Fluid Dyn. Res. 38 (6), 359.CrossRefGoogle Scholar
Ng, C.-O. 2006 b Dispersion in steady and oscillatory flows through a tube with reversible and irreversible wall reactions. Proc. R. Soc. A 462 (2066), 481–515.CrossRefGoogle Scholar
Nordanger, H., Morozov, A. & Stenhammar, J. 2022 Anisotropic diffusion of ellipsoidal tracers in microswimmer suspensions. Phys. Rev. Fluids 7 (1), 013103.CrossRefGoogle Scholar
Omori, T., Kikuchi, K., Schmitz, M., Pavlovic, M., Chuang, C.-H. & Ishikawa, T. 2022 Rheotaxis and migration of an unsteady microswimmer. J. Fluid Mech. 930, A30.CrossRefGoogle Scholar
Pavliotis, G.A. 2008 Multiscale Methods. Texts Applied in Mathematics, vol. 53. Springer.Google Scholar
Pedley, T.J. 2010 Collective behaviour of swimming micro-organisms. Exp. Mech. 50 (9), 1293–1301.CrossRefGoogle Scholar
Pedley, T.J. & Kessler, J.O. 1992 Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24 (1), 313–358.CrossRefGoogle Scholar
Perrin, F. 1936 Mouvement Brownien d'un ellipsoide (II). Rotation libre et dépolarisation des fluorescences. Translation et diffusion de molécules ellipsoidales. J. Phys. Radium 7 (1), 1–11.CrossRefGoogle Scholar
Purcell, E.M. 1997 The efficiency of propulsion by a rotating flagellum. Proc. Natl Acad. Sci. 94 (21), 11307–11311.CrossRefGoogle ScholarPubMed
Rothschild, 1963 Non-random distribution of bull spermatozoa in a drop of sperm suspension. Nature 198 (4886), 1221–1222.CrossRefGoogle Scholar
Rusconi, R., Guasto, J.S. & Stocker, R. 2014 Bacterial transport suppressed by fluid shear. Nat. Phys. 10 (3), 212–217.CrossRefGoogle Scholar
Saintillan, D. & Shelley, M.J. 2013 Active suspensions and their nonlinear models. C. R. Phys. 14 (6), 497–517.CrossRefGoogle Scholar
Shen, Z., Farutin, A., Thiébaud, M. & Misbah, C. 2017 Interaction and rheology of vesicle suspensions in confined shear flow. Phys. Rev. Fluids 2 (10), 103101.CrossRefGoogle Scholar
Thiffeault, J.-L. & Guo, J. 2022 Anisotropic active Brownian particle with a fluctuating propulsion force. Phys. Rev. E 106 (1), L012603.CrossRefGoogle ScholarPubMed
Traverso, T. & Michelin, S. 2022 Collective dynamics and rheology of confined phoretic suspensions. J. Fluid Mech. 943, A21.CrossRefGoogle Scholar
Vennamneni, L., Nambiar, S. & Subramanian, G. 2020 Shear-induced migration of microswimmers in pressure-driven channel flow. J. Fluid Mech. 890, A15.CrossRefGoogle Scholar
Volpe, G., Gigan, S. & Volpe, G. 2014 Simulation of the active Brownian motion of a microswimmer. Am. J. Phys. 82 (7), 659–664.CrossRefGoogle Scholar
Wang, B., Jiang, W. & Chen, G. 2022 a Cross-channel distribution and streamwise dispersion of micro-swimmers in a vertical channel flow: A study on the effects of shear, particle shape, and convective inertial torque. Phys. Fluids 34 (1), 011904.CrossRefGoogle Scholar
Wang, B., Jiang, W. & Chen, G. 2022 b Gyrotactic trapping of micro-swimmers in simple shear flows: a study directly from the fundamental Smoluchowski equation. J. Fluid Mech. 939, A37.CrossRefGoogle Scholar
Wang, B., Jiang, W. & Chen, G. 2023 Dispersion of a gyrotactic micro-organism suspension in a vertical pipe: the buoyancy–flow coupling effect. J. Fluid Mech. 962, A39.CrossRefGoogle Scholar
Wang, B., Jiang, W., Chen, G. & Tao, L. 2022 c Transient dispersion in a channel with crossflow and wall adsorption. Phys. Rev. Fluids 7 (7), 074501.CrossRefGoogle Scholar
Wang, P. & Cirpka, O.A. 2021 Surface transient storage under low-flow conditions in streams with rough bathymetry. Water Resour. Res. 57 (12), e2021WR029899.CrossRefGoogle Scholar
Wu, Z. & Chen, G. 2014 Approach to transverse uniformity of concentration distribution of a solute in a solvent flowing along a straight pipe. J. Fluid Mech. 740, 196–213.CrossRefGoogle Scholar
Yang, Y., Verzicco, R., Lohse, D. & Caulfield, C.P. 2022 Layering and vertical transport in sheared double-diffusive convection in the diffusive regime. J. Fluid Mech. 933, A30.CrossRefGoogle Scholar
Yasuda, H. 1984 Longitudinal dispersion of matter due to the shear effect of steady and oscillatory currents. J. Fluid Mech. 148, 383–403.CrossRefGoogle Scholar
Zeng, L., Jiang, W. & Pedley, T.J. 2022 Sharp turns and gyrotaxis modulate surface accumulation of microorganisms. Proc. Natl Acad. Sci. 119 (42), e2206738119.CrossRefGoogle ScholarPubMed
Zhan, J., Jiang, W. & Wu, Z. 2024 Reactive transport in open-channel flows with bed adsorption and desorption. J. Hydrol. 632, 130855.CrossRefGoogle Scholar