Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-18T17:41:40.946Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-classical gas dynamics of vapour mixtures

Published online by Cambridge University Press:  13 February 2014

Alberto Guardone ,
Piero Colonna ,
Emiliano Casati  and
Enrico Rinaldi
Alberto Guardone
Affiliation:
Department of Aerospace Science and Technology, Politecnico di Milano, Via La Masa 34, Milano, 20156, Italy
Piero Colonna*
Affiliation:
Propulsion and Power, Delft University of Technology, Kluyverweg 1, Delft, 2629 HS, The Netherlands
Emiliano Casati
Affiliation:
Propulsion and Power, Delft University of Technology, Kluyverweg 1, Delft, 2629 HS, The Netherlands Energy Department, Politecnico di Milano, Via Lambruschini 4, Milano, 20156, Italy
Enrico Rinaldi
Affiliation:
Process and Energy Department, Delft University of Technology, Leeghwaterstraat 39, 2628 CB, Delft, The Netherlands
*
†Email address for correspondence: P.Colonna@TUDelft.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

The non-classical gas dynamics of binary mixtures of organic fluids in the vapour phase is investigated for the first time. A predictive thermodynamic model is used to compute the relevant mixture properties, including its critical point coordinates and the local value of the fundamental derivative of gas dynamics 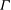$\Gamma $. The considered model is the improved Peng–Robinson Stryjek–Vera cubic equation of state, complemented by the Wong–Sandler mixing rules. A finite thermodynamic region is found where the nonlinearity parameter 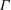$\Gamma $ is negative and therefore non-classical gas dynamics phenomena are admissible. A non-monotone dependence of $\Gamma $ on the mixture composition is observed in the case of binary mixtures of siloxane and perfluorocarbon fluids, with the minimum value of 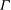$\Gamma $ in the mixture being always larger than that of its more complex component. The observed dependence indicates that non-ideal mixing has a strong influence on the gas dynamics behaviour, either classical or non-classical, of the mixture. Numerical experiments of the supersonic expansion of a mixture flow around a sharp corner show the transition from the classical configuration, exhibiting an isentropic rarefaction fan centred at the expansion corner, to non-classical ones, including mixed expansion waves and rarefaction shock waves, if the mixture composition is changed.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Gas dynamics Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 741 , 25 February 2014 , pp. 681 - 701
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbott, M. M. 1973 Cubic equations of state. AIChE J. 19, 596–601.Google Scholar
Aldo, A. & Argrow, B. 1995 Dense gas flow in minimum length nozzles. Trans. ASME I: J. Fluids Engng 117 (2), 270–276.Google Scholar
Angelino, G. & Colonna, P. 1998 Multicomponent working fluids for organic Rankine cycles (${\mathrm{ORC}}_{\mathrm{s}}$). Energy 23 (6), 449–463.CrossRefGoogle Scholar
Angelino, G. & Colonna, P. 2000 Air cooled siloxane bottoming cycle for molten carbonate fuel cells. In Fuel Cell Seminar pp. 667–670.Google Scholar
Angelino, G. & Invernizzi, C. 1993 Cyclic methylsiloxanes as working fluids for space power cycles. Trans. ASME: J. Sol. Energy 115 (3), 130–137.Google Scholar
Argrow, B. M. 1996 Computational analysis of dense gas shock tube flow. Shock Waves 6, 241–248.Google Scholar
Armenio, A.2009 Siloxane/perfuorocarbon mixtures as working fuid for organic Rankine cycle turbogenerators. Master’s thesis (Report ET-2365), Politecnico di Milano - Delft University of Technology.Google Scholar
Bethe, H. A.1942 The theory of shock waves for an arbitrary equation of state. Technical Report 545. Office Sci. Res. & Dev.Google Scholar
Borisov, A. A., Borisov, Al. A., Kutateladze, S. S. & Nakoryakov, V. E. 1983 Rarefaction shock waves near the critic liquid–vapour point. J. Fluid Mech. 126, 59–73.Google Scholar
Brown, B. & Argrow, B. 1997 Two-dimensional shock tube flow for dense gases. J. Fluid Mech. 349, 95–115.CrossRefGoogle Scholar
Brown, B. & Argrow, B. 1998 Nonclassical dense gas flows for simple geometries. AIAA J. 36 (10), 1842–1847.Google Scholar
Brown, B. & Argrow, B. 2000 Application of Bethe–Zel’dovich–Thompson fluids in organic Rankine cycle engines. J. Propul. Power 16 (6), 1118–1124.Google Scholar
Bymaster, A., Emborsky, C., Dominik, A. & Chapman, W. 2008 Renormalization-group corrections to a perturbed-chain statistical associating fluid theory for pure fluids near to and far from the critical region. Ind. Engng Chem. Res. 47 (16), 6264–6274.CrossRefGoogle Scholar
Callen, H. B. 1985 Thermodynamics and an Introduction to Thermostatistics. 2nd edn. Wiley.Google Scholar
Chandrasekar, D. & Prasad, P. 1991 Transonic flow of a fluid with positive and negative nonlinearity through a nozzle. Phys. Fluids A 3 (3), 427–438.Google Scholar
Chen, H., Goswami, D. Y., Rahman, M. M. & Stefanakos, E. K. 2011 A supercritical Rankine cycle using zeotropic mixture working fluids for the conversion of low-grade heat into power. Energy 36 (1), 549–555.Google Scholar
Cinnella, P. 2008 Transonic flows of dense gases over finite wings. Phys. Fluids 20 (4).Google Scholar
Cinnella, P. & Congedo, P. M. 2007 Inviscid and viscous aerodynamics of dense gases. J. Fluid Mech. 580, 179–217.Google Scholar
Cinnella, P. & Congedo, P. M. 2008 Optimal airfoil shapes for viscous transonic flows of Bethe–Zel’dovich–Thompson fluids. Comput. Fluids 37, 250–264.CrossRefGoogle Scholar
Colonna, P.1996 Fluidi di lavoro multi componenti per cicli termodinamici di potenza (multicomponent working fluids for power cycles). PhD thesis, Politecnico di Milano.Google Scholar
Colonna, P. & Guardone, A. 2006 Molecular interpretation of nonclassical gas dynamics of dense vapors under the van der Waals model. Phys. Fluids 18 (5), 056101.CrossRefGoogle Scholar
Colonna, P., Guardone, A. & Nannan, N. R. 2007 Siloxanes: a new class of candidate Bethe–Zel’dovich–Thompson fluids. Phys. Fluids 19 (8), 086102.Google Scholar
Colonna, P., Guardone, A., Nannan, N. R. & Zamfirescu, C. 2008a Design of the dense gas flexible asymmetric shock tube. Trans. ASME I: J. Fluids Engng 130 (3), 034501.Google Scholar
Colonna, P., Nannan, N. R. & Guardone, A. 2008b Multiparameter equations of state for siloxanes: $[(\textrm {CH}_3)_3\mbox{--}\textrm {Si}\mbox{--}\textrm {O}_{1/2} ]_2 \mbox{--} [\textrm {O-Si}\mbox{--}(\textrm {CH}_3)_2]_{i=1,\dots,3}$ and $[\textrm {O}\mbox{--}\textrm {Si}\mbox{--}(\textrm {CH}_3)_2]_6$. Fluid Phase Equilib. 263 (2), 115–130.CrossRefGoogle Scholar
Colonna, P., Nannan, N. R., Guardone, A. & Lemmon, E. W. 2006 Multiparameter equations of state for selected siloxanes. Fluid Phase Equilib. 244, 193–211.CrossRefGoogle Scholar
Colonna, P., Nannan, N. R., Guardone, A. & van der Stelt, T. P. 2009 On the computation of the fundamental derivative of gas dynamics using equations of state. Fluid Phase Equilib. 286 (1), 43–54.Google Scholar
Colonna, P. & Silva, P. 2003 Dense gas thermodynamic properties of single and multicomponent fluids for fluid dynamics simulations. Trans. ASME I: J. Fluids Engng 125 (3), 414–427.Google Scholar
Colonna, P., van der Stelt, T. P. & Guardone, A.2012 FluidProp (Version 3.0): A program for the estimation of thermophysical properties of fluids. http://www.fluidprop.com/, a program since 2004.Google Scholar
Congedo, P., Colonna, P., Corre, C., Witteveen, J. & Iaccarino, G. 2012 Backward uncertainty propagation method in flow problems: application to the prediction of rarefaction shock waves. Comput. Meth. Appl. Engng 213–216, 314–326.Google Scholar
Coutsikos, P., Kalospiros, N. & Tassios, D. 1995 Capabilities and limitations of the Wong–Sandler mixing rules. Fluid Phase Equilib. 108 (1–2), 59–78.CrossRefGoogle Scholar
Cramer, M. & Kluwick, A. 1984 On the propagation of waves exhibiting both positive and negative nonlinearity. J. Fluid Mech. 142, 9–37.Google Scholar
Cramer, M. S. 1989 Negative nonlinearity in selected fluorocarbons. Phys. Fluids 1 (11), 1894–1897.CrossRefGoogle Scholar
Cramer, M. S. 1991 Nonclassical dynamics of classical gases. In Nonlinear Waves in Real Fluids (ed. Kluwick, A.), pp. 91–145. Springer-Verlag.Google Scholar
Cramer, M. S. & Best, L. M. 1991 Steady, isentropic flows of dense gases. Phys. Fluids 3 (1), 219–226.CrossRefGoogle Scholar
Cramer, M. S. & Crickenberger, A. B. 1991 The dissipative structure of shock waves in dense gases. J. Fluid Mech. 223, 325–355.Google Scholar
Cramer, M. S. & Sen, R. 1986 Shock formation in fluids having embedded regions of negative nonlinearity. Phys. Fluids 29, 2181–2191.CrossRefGoogle Scholar
Cramer, M. S. & Sen, R. 1987 Exact solutions for sonic shocks in van der Waals gas. Phys. Fluids 30 (2), 377–385.Google Scholar
Cramer, M. S. & Sen, R. 1990 Mixed nonlinearity and double shocks in superfluid helium. J. Fluid Mech. 221, 233–261.Google Scholar
Cramer, M. S., Tarkenton, L. M. & Tarkenton, G. M. 1992 Critical Mach number estimates for dense gases. Phys. Fluids 4 (8), 1840–1847.Google Scholar
Dvornic, P. R. 2004 In Silicon Compounds: Silanes and Silicones High temperature stability of polysiloxanes, pp. 419–432. Gelest Inc.Google Scholar
Fergason, S. H.2001 Dense gas shock tube: design and analysis. PhD thesis, University of Colorado, Boulder.Google Scholar
Fergason, S. H., Guardone, A. & Argrow, B. M. 2003 Construction and validation of a dense gas shock tube. J. Thermophys. Heat Transfer 17 (3), 326–333.Google Scholar
Fergason, S. H., Ho, T. L., Argrow, B. M. & Emanuel, G. 2001 Theory for producing a single-phase rarefaction shock wave in a shock tube. J. Fluid Mech. 445, 37–54.Google Scholar
Ghosh, P. & Taraphdar, T. 1998 Prediction of vapor–liquid equilibria of binary systems using PRSV equation of state and Wong-Sandler mixing rules. Chem. Eng. J. 70 (1), 15–24.Google Scholar
Gross, J. & Sadowski, G. 2001 Perturbed-chain SAFT: An equation of state based on a perturbation theory for chain molecules. Ind. Engng Chem. Res. 40 (4), 1244–1260.Google Scholar
Guardone, A. 2007 Three-dimensional shock tube flows of dense gases. J. Fluid Mech. 583, 423–442.Google Scholar
Guardone, A., Zamfirescu, C. & Colonna, P. 2010 Maximum intensity of rarefaction shock waves for dense gases. J. Fluid Mech. 642 (1), 127–146.Google Scholar
Gulen, S. C., Thompson, P. A. & Cho, H. A. 1989 Rarefaction and liquefaction shock waves in regular and retrograde fluids with near-critical end states. In Adiabatic Waves in Liquid–vapor Systems pp. 281–290. Springer-Verlag.Google Scholar
Hayes, W. 1960 The basic theory of gasdynamic discontinuities. In Fundamentals of Gasdynamics: High Speed Aerodynamics and Jet Propulsion (ed. Emmons, H. W.), vol. 3, pp. 416–481. Princeton University Press.Google Scholar
Ivanov, A. G. & Novikov, S. A. 1961 Rarefaction shock waves in iron and steel. Zh. Eksp. Teor. Fiz. 40 (6), 1880–1882.Google Scholar
Kluwick, A. 2001 Theory of shock waves. Rarefaction shocks. In Handbook of Shockwaves vol. 1, chap. 3.4, pp. 339–411. Academic Press.Google Scholar
Kluwick, A. & Meyer, G. 2010 Shock regularization in dense gases by viscous-inviscid interactions. J. Fluid Mech. 644, 473–507.CrossRefGoogle Scholar
Kunz, O., Klimeck, R., Wagner, W. & Jaeschke, M. 2007 2007 The GERG-2004 wide-range equation of state for natural gases and other mixtures Tech. Rep. GERG Technical Monograph, vol. 15, VDI-Verlag.Google Scholar
Kutateladze, S. S., Nakoryakov, V. E. & Borisov, A. A. 1987 Rarefaction waves in liquid and gas–liquid media. Annu. Rev. Fluid Mech. 19, 577–600.Google Scholar
Lai, N., Wendland, M. & Fischer, J. 2009 Description of linear siloxanes with PC-SAFT equation. Fluid Phase Equilib. 283 (1–2), 22–30.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Course of Theoretical Physics, Fluid Mechanics. vol. 6. Pergamon Press.Google Scholar
Lang, W., Almbauer, R. & Colonna, P. 2013 Assessment of waste heat recovery for a heavy-duty truck engine using an ORC turbogenerator. J. Engng Gas Turbines Power 135 (4), 042313.Google Scholar
Menikoff, R. & Plohr, B. J. 1989 The Riemann problem for fluid flow of real material. Rev. Mod. Phys. 61 (1), 75–130.CrossRefGoogle Scholar
Monaco, J., Cramer, M. & Watson, L. 1997 Supersonic flows of dense gases in cascade configurations. J. Fluid Mech. 330, 31–59.Google Scholar
Nannan, N. R., Colonna, P., Tracy, C. M., Rowley, R. L. & Hurly, J. J. 2007 Ideal-gas heat capacities of dimethylsiloxanes from speed-of-sound measurements and ab initio calculations. Fluid Phase Equilib. 257 (1), 102–113.Google Scholar
Nannan, N. R., Guardone, A. & Colonna, P. 2013 On the fundamental derivative of gas dynamics in the vapor–liquid critical region of single-component typical fluids. Fluid Phase Equilib. 337, 259–273.Google Scholar
Nannan, R. N. & Colonna, P. 2009 Improvement on multiparameter equations of state for dimethylsiloxanes by adopting more accurate ideal-gas isobaric heat capacities. Fluid Phase Equilib. 280 (1–2), 151–152.Google Scholar
Pecnik, R., Rinaldi, E. & Colonna, P. 2012 Computational fluid dynamics of a radial compressor operating with supercritical $\mathrm{CO}_2$. Trans. ASME: J. Engng Gas Turbines Power 134, 122301.Google Scholar
Pecnik, R., Terrapon, V. E., Ham, F., Iaccarino, G. & Pitsch, H. 2012 Reynolds-Averaged Navier–Stokes Simulations of the Hyshot II Scramjet. AIAA J. 50 (8), 1717–1732.Google Scholar
Peng, D. Y. & Robinson, D. B. 1976 A new two-constant equation of state. Ind. Engng Chem. Fundam. 15 (1), 59–64.Google Scholar
Proust, P. & Vera, J. H. 1989 PRSV: the Stryjek–Vera modification of the Peng–Robinson equation of state. Parameters for other pure compounds of industrial interest. Can. J. Chem. Engng. 67 (1), 170–173.CrossRefGoogle Scholar
Renon, H. & Prausnitz, J. M. 1968 Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 14 (1), 135–144.Google Scholar
Sandler, S. I. 1989 Chemical and Engineering Thermodynamics. 2nd edn. John Wiley and Sons.Google Scholar
Sandler, S. I. 1993 Models for Thermodynamic and Phase Equilibria Calculations. CRC Press.Google Scholar
Schnerr, G. & Molokov, S. 1994 Exact solutions for transonic flows of dense gases in two-dimensional and axisymmetric nozzles. Phys. Fluids 6 (10), 3465–3472.Google Scholar
Schnerr, G. & Molokov, S. 1995 Nonclassical effects in two-dimensional transonic flows. Phys. Fluids 7 (11), 2867–2875.CrossRefGoogle Scholar
Schnerr, G. H. & Leidner, P. 1993a Numerical investigation of axial cascades for dense gases. In PICAST’1–Pacific International Conference on Aerospace Science Technology, National Cheng Kung University, Taiwan, Republic of China (ed. Chin, E. L.), vol. 2, pp. 818–825.Google Scholar
Schnerr, G. H. & Leidner, P. 1993b Two-dimensional nozzle flow of dense gases. In Fluids Engineering Conference Washington, DC.Google Scholar
Soave, G. 1972 Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Engng Sci. 27, 1197–1203.Google Scholar
Stryjek, R. & Vera, J. H. 1986 PRSV: An improved Peng–Robinson equation of state for pure compounds and mixtures. Can. J. Chem. Engng. 64 (2), 323–333.CrossRefGoogle Scholar
Thompson, P. A. 1971 A fundamental derivative in gasdynamics. Phys. Fluids 14 (9), 1843–1849.Google Scholar
Thompson, P. A. 1988 Compressilbe Fluid Dynamics. McGraw-Hill.Google Scholar
Thompson, P. A. 1991 Liquid–vapor adiabatic phase changes and related phenomena. In Nonlinear Waves in Real Fluids (ed. Kluwick, A.), pp. 147–213. Springer-Verlag.Google Scholar
Thompson, P. A., Carofano, G. A. & Kim, Y. G. 1986 Shock waves and phase changes in a large heat capacity fluid emerging from a tube. J. Fluid Mech. 166, 57–96.Google Scholar
Thompson, P. A. & Lambrakis, K. C. 1973 Negative shock waves. J. Fluid Mech. 60, 187–208.Google Scholar
Thompson, P. A. & Loutrel, W. F. 1973 Opening time of brittle shock-tube diaphragms for dense fluids. Rev. Sci. Instrum. 44 (9), 1436–1437.Google Scholar
Trapp, C. & Colonna, P. 2013 Efficiency improvement in pre-combustion $\mathrm{CO}_2$ removal units with a waste-heat recovery ORC power plant. J. Engng Gas Turbines Power 135 (4), 04231.Google Scholar
Uusitalo, A., Turunen-Saaresti, T., Honkatukia, J., Colonna, P. & Larjola, J. 2013 Siloxanes as working fluids for a mini-ORC systems based on high-speed turbogenerator technology. Trans. ASME: J. Engng Gas Turbines Power 135 (4), 042305–042319.Google Scholar
van der Stelt, T. P, Nannan, N. R. & Colonna, P. 2012 The iPRSV equation of state. Fluid Phase Equilib. 330, 24–35.Google Scholar
van der Waals, J. D. 1988 On the Continuity of the Gaseous and Liquid States. vol. XIV. North-Holland, reprinted.Google Scholar
Weyl, H. 1949 Shock waves in arbitrary fluids. Commun. Pure Appl. Maths 2, 102–122.Google Scholar
Wong, D. S. H. & Sandler, S. I. 1992 A theoretically correct mixing rule for cubic equations of state. AIChE J. 38 (5), 671–680.Google Scholar
Zamfirescu, C., Guardone, A. & Colonna, P. 2008 Admissibility region for rarefaction shock waves in dense gases. J. Fluid Mech. 599, 363–381.Google Scholar
Zel’dovich, Y. 1946 On the possibility of rarefaction shock waves. Zh. Eksp. Teor. Fiz. 4, 363–364.Google Scholar