Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Padovan, Alberto
Otto, Samuel E.
and
Rowley, Clarence W.
2020.
Analysis of amplification mechanisms and cross-frequency interactions in nonlinear flows via the harmonic resolvent.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
McKeon, B. J.
2020.
A basis for flow modelling.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Schmidt, Oliver T.
2020.
Bispectral mode decomposition of nonlinear flows.
Nonlinear Dynamics,
Vol. 102,
Issue. 4,
p.
2479.
Li, Zhihui
and
Agarwal, Ramesh K.
2021.
Investigation of endwall effect on transitional flow inside compressor cascade passage at low Reynolds number.
Physics of Fluids,
Vol. 33,
Issue. 11,
Jovanović, Mihailo R.
2021.
From Bypass Transition to Flow Control and Data-Driven Turbulence Modeling: An Input–Output Viewpoint.
Annual Review of Fluid Mechanics,
Vol. 53,
Issue. 1,
p.
311.
Barthel, Benedikt
Zhu, Xiaojue
and
McKeon, Beverley
2021.
Closing the loop: nonlinear Taylor vortex flow through the lens of resolvent analysis.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Jin, Bo
Symon, Sean
and
Illingworth, Simon J.
2021.
Energy transfer mechanisms and resolvent analysis in the cylinder wake.
Physical Review Fluids,
Vol. 6,
Issue. 2,
Herrmann, Benjamin
Baddoo, Peter J.
Semaan, Richard
Brunton, Steven L.
and
McKeon, Beverley J.
2021.
Data-driven resolvent analysis.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Oz, Furkan
and
Kara, Kursat
2021.
A CFD Tutorial in Julia: Introduction to Laminar Boundary-Layer Theory.
Fluids,
Vol. 6,
Issue. 6,
p.
207.
Oz, Furkan
and
Kara, Kursat
2021.
A CFD Tutorial in Julia: Introduction to Compressible Laminar Boundary-Layer Flows.
Fluids,
Vol. 6,
Issue. 11,
p.
400.
Bengana, Yacine
and
Tuckerman, Laurette S.
2021.
Frequency prediction from exact or self-consistent mean flows.
Physical Review Fluids,
Vol. 6,
Issue. 6,
Gopalakrishnan, Shyam Sunder
and
Mandal, Alakesh Chandra
2021.
Transient growth in a flat plate boundary layer under a stream with uniform shear.
Physics of Fluids,
Vol. 33,
Issue. 11,
Guo, Peixu
Shi, Fangcheng
Gao, Zhenxun
Jiang, Chongwen
Lee, Chun-Hian
and
Wen, Chihyung
2022.
Sensitivity analysis on supersonic-boundary-layer stability: Parametric influence, optimization, and inverse design.
Physics of Fluids,
Vol. 34,
Issue. 10,
Barthel, Benedikt
Gomez, Salvador
and
McKeon, Beverley J.
2022.
Variational formulation of resolvent analysis.
Physical Review Fluids,
Vol. 7,
Issue. 1,
Dwivedi, Anubhav
Sidharth, G.S.
and
Jovanović, Mihailo R.
2022.
Oblique transition in hypersonic double-wedge flow.
Journal of Fluid Mechanics,
Vol. 948,
Issue. ,
Skene, Calum S.
Yeh, Chi-An
Schmid, Peter J.
and
Taira, Kunihiko
2022.
Sparsifying the resolvent forcing mode via gradient-based optimisation.
Journal of Fluid Mechanics,
Vol. 944,
Issue. ,
Towne, Aaron
Rigas, Georgios
Kamal, Omar
Pickering, Ethan
and
Colonius, Tim
2022.
Efficient global resolvent analysis via the one-way Navier–Stokes equations.
Journal of Fluid Mechanics,
Vol. 948,
Issue. ,
Padovan, Alberto
and
Rowley, Clarence W.
2022.
Analysis of the dynamics of subharmonic flow structures via the harmonic resolvent: Application to vortex pairing in an axisymmetric jet.
Physical Review Fluids,
Vol. 7,
Issue. 7,
Poulain, Arthur
Content, Cédric
Sipp, Denis
Rigas, Georgios
and
Garnier, Eric
2023.
BROADCAST: A high-order compressible CFD toolbox for stability and sensitivity using Algorithmic Differentiation.
Computer Physics Communications,
Vol. 283,
Issue. ,
p.
108557.
Guo, Peixu
Hao, Jiaao
and
Wen, Chih-Yung
2023.
Interaction and breakdown induced by multiple optimal disturbances in hypersonic boundary layer.
Journal of Fluid Mechanics,
Vol. 974,
Issue. ,
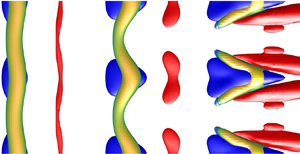
 $K$-type and
$K$-type and  $H$-type mechanisms, including oblique and planar Tollmien–Schlichting waves, streaks and their breakdown. We show that nonlinearity plays a critical role in optimising growth by combining and redistributing energy between the linear mechanisms and the higher perturbation harmonics. With a very limited range of frequencies and wavenumbers, the calculations appear to reach the early stages of the turbulent regime through the generation and breakdown of hairpin and quasi-streamwise staggered vortices.
$H$-type mechanisms, including oblique and planar Tollmien–Schlichting waves, streaks and their breakdown. We show that nonlinearity plays a critical role in optimising growth by combining and redistributing energy between the linear mechanisms and the higher perturbation harmonics. With a very limited range of frequencies and wavenumbers, the calculations appear to reach the early stages of the turbulent regime through the generation and breakdown of hairpin and quasi-streamwise staggered vortices.


