1. Introduction
Taylor–Couette flow (TCF) is perhaps among the most studied flows in fluid mechanics. In the 100 years since Taylor's monumental work (Taylor Reference Taylor1923), it has provided an excellent testing ground for theoretical, experimental and numerical studies of rotating shear flows. How shear and Coriolis forces alter flow characteristics is important in various applications, and TCF was designed so that they can be adjusted easily by changing the rotation speed of the inner and outer cylinders. Researchers have long been fascinated by the numerous metastable flow patterns observed in the relatively low-Taylor-number regime (e.g. Andereck, Liu & Swinney Reference Andereck, Liu and Swinney1986). On the other hand, it was only a decade ago that the study of high-Taylor-number flows became active. Great efforts were made to investigate the nature of turbulence in the parameter space by means of high-Taylor-number experiments (e.g. Dennis et al. Reference Dennis, Huisman, Bruggert, Sun and Lohse2011; Paoletti & Lathrop Reference Paoletti and Lathrop2011; van Gils et al. Reference van Gils, Huisman, Bruggert, Sun and Lohse2011, Reference van Gils, Huisman, Grossmann, Sun and Lohse2012; Huisman et al. Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) and direct numerical simulations (e.g. Ostilla et al. Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013; Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2013, Reference Brauckmann and Eckhardt2017; Ostilla-Mónico et al. Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohseb). As summarised in the review paper by Grossmann, Lohse & Sun (Reference Grossmann, Lohse and Sun2016), and in fact seen in the pioneering experiments by Lathrop, Fineberg & Swinney (Reference Lathrop, Fineberg and Swinney1992) and Lewis & Swinney (Reference Lewis and Swinney1999), fully developed turbulence has a surprisingly clean asymptotic character, while there seems to be no definitive Navier–Stokes-based theory to explain it.
This study aims to reveal the asymptotic properties of steady axisymmetric solutions at high Taylor numbers and to compare them with the experimental and numerical results. The analysis of such solutions, known as Taylor vortex solutions, goes back to the weakly nonlinear analysis, for example, by Davey (Reference Davey1962). With modern computational power, it is possible to calculate solutions up to the Taylor number used in the experiments. Of course, the use of Newton's method is essential as the solution is unstable in the high-Taylor-number regime.
The idea that an unstable solution with a relatively simple structure with respect to time can capture some characteristics of turbulence is not as absurd as one might think. It is well known in dynamical systems theory that chaotic dynamics can be approximated by a sufficiently large number of periodic orbits (see e.g. Cvitanović et al. Reference Cvitanović, Artuso, Mainieri, Tanner and Vattay2012). For moderate Reynolds number shear flows, it was reported repeatedly that a good approximation of the turbulent dynamics can be obtained with a small number of periodic orbits (Kawahara, Uhlmann & van Veen Reference Kawahara, Uhlmann and van Veen2012; Willis, Cvitanović & Avila Reference Willis, Cvitanović and Avila2013; Krygier, Pughe-Sanford & Grigoriev Reference Krygier, Pughe-Sanford and Grigoriev2021). In phase space, these periodic orbits usually appear with stationary or travelling wave solutions in their vicinity. The advantage of focusing on simple solutions is that their asymptotic nature may be justified theoretically by mathematical analyses. Over the past decade, it has been established that the matched asymptotic expansion is a powerful tool in understanding the behaviour of steady or travelling wave solutions in shear flows (Hall & Sherwin Reference Hall and Sherwin2010; Deguchi, Hall & Walton Reference Deguchi, Hall and Walton2013; Deguchi & Hall Reference Deguchi and Hall2014a,Reference Deguchi and Hallb; Deguchi Reference Deguchi2015; Dempsey et al. Reference Dempsey, Deguchi, Hall and Walton2016; Deguchi & Walton Reference Deguchi and Walton2018). Therefore if we are allowed to assume that there is a simple solution that roughly captures the scaling properties of turbulence within the vast phase space, then there is hope for a logical explanation of the scaling from first principles.
In the high-Taylor-number numerical and experimental studies, the parameter dependence of angular momentum transport was a major focus. The driving force behind those studies was the ‘analogy’ between turbulent Rayleigh–Bénard convection (RBC) and TCF. This analogy was well known at least in the 1960s, and has risen and fallen throughout the history of turbulence research (Bradshaw Reference Bradshaw1969; Dubrulle & Hersant Reference Dubrulle and Hersant2002). Recent studies have been influenced by Eckhardt, Grossmann & Lohse (Reference Eckhardt, Grossmann and Lohse2007), who argued that the phenomenology of RBC turbulence proposed by Grossmann & Lohse (Reference Grossmann and Lohse2000) can be applied to TCF as well. Shortly after, the aforementioned high-Taylor-number TCF experiments confirmed that the scaling of the Nusselt number ![]() $Nu$ is similar to that observed for RBC by He et al. (Reference He, Funfschilling, Nobach, Bodenschatz and Guenter2012) (
$Nu$ is similar to that observed for RBC by He et al. (Reference He, Funfschilling, Nobach, Bodenschatz and Guenter2012) (![]() $Nu$ for TCF is defined as the torque on the cylinder wall normalised by its laminar value). It should be remarked that despite the analogy that has been believed, this similarity in the ultimate scaling is actually not at all obvious. As pointed out, for example, by Chandrasekhar (Reference Chandrasekhar1961), Robinson (Reference Robinson1967), Veronis (Reference Veronis1970) and Lezius & Johnston (Reference Lezius and Johnston1976), for the two flows to be equivalent, they must be at least axisymmetric. Moreover, the exact equivalence of the two flows requires an infinitesimally narrow cylinder gap, co-rotating cylinders, and Prandtl number unity.
$Nu$ for TCF is defined as the torque on the cylinder wall normalised by its laminar value). It should be remarked that despite the analogy that has been believed, this similarity in the ultimate scaling is actually not at all obvious. As pointed out, for example, by Chandrasekhar (Reference Chandrasekhar1961), Robinson (Reference Robinson1967), Veronis (Reference Veronis1970) and Lezius & Johnston (Reference Lezius and Johnston1976), for the two flows to be equivalent, they must be at least axisymmetric. Moreover, the exact equivalence of the two flows requires an infinitesimally narrow cylinder gap, co-rotating cylinders, and Prandtl number unity.
It is an interesting question, then, to forget the latter three conditions and ask whether the analogy in the sense of the ![]() $Nu$ scaling holds for an axisymmetric Taylor vortex and a two-dimensional roll cell. The equations governing both flows are not the same, but they certainly have a similar structure. Many researchers have studied theoretically the large-Rayleigh-number nature of roll cells in RBC over the years; see Pillow (Reference Pillow1952), Robinson (Reference Robinson1967), Wesseling (Reference Wesseling1969), Chini & Cox (Reference Chini and Cox2009) and Hepworth (Reference Hepworth2014) for constant Prandtl number flows, and Roberts (Reference Roberts1979), Jimenez & Zufiria (Reference Jimenez and Zufiria1987) and Vynnycky & Masuda (Reference Vynnycky and Masuda2013) for asymptotically large Prandtl number flows. Waleffe, Boonkasame & Smith (Reference Waleffe, Boonkasame and Smith2015) and Sondak, Smith & Waleffe (Reference Sondak, Smith and Waleffe2015) shortened the wavelength of the RBC roll cell and found that there is a special wavelength at which the Nusselt number reaches a maximum value. Interestingly, this optimised Nusselt number is close to that obtained experimentally, although the Rayleigh number that they used is much lower than the one used by He et al. (Reference He, Funfschilling, Nobach, Bodenschatz and Guenter2012). More recently, Wen, Goluskin & Doering (Reference Wen, Goluskin and Doering2022) continued the same solution branch to higher Rayleigh numbers and claimed that the maximum Nusselt number corresponds to the so-called classical scaling, where the Nusselt number is proportional to the Rayleigh number to the power of one-third (Malkus Reference Malkus1954; Priestley Reference Priestley1954; Grossmann & Lohse Reference Grossmann and Lohse2000; Kawano et al. Reference Kawano, Motoki, Shimizu and Kawahara2021). The study by Kooloth, Sondak & Smith (Reference Kooloth, Sondak and Smith2021) confirmed that roll cells with different wavelengths play important roles in two-dimensionally restricted RBC turbulence. This paper is motivated by all of the above RBC studies.
$Nu$ scaling holds for an axisymmetric Taylor vortex and a two-dimensional roll cell. The equations governing both flows are not the same, but they certainly have a similar structure. Many researchers have studied theoretically the large-Rayleigh-number nature of roll cells in RBC over the years; see Pillow (Reference Pillow1952), Robinson (Reference Robinson1967), Wesseling (Reference Wesseling1969), Chini & Cox (Reference Chini and Cox2009) and Hepworth (Reference Hepworth2014) for constant Prandtl number flows, and Roberts (Reference Roberts1979), Jimenez & Zufiria (Reference Jimenez and Zufiria1987) and Vynnycky & Masuda (Reference Vynnycky and Masuda2013) for asymptotically large Prandtl number flows. Waleffe, Boonkasame & Smith (Reference Waleffe, Boonkasame and Smith2015) and Sondak, Smith & Waleffe (Reference Sondak, Smith and Waleffe2015) shortened the wavelength of the RBC roll cell and found that there is a special wavelength at which the Nusselt number reaches a maximum value. Interestingly, this optimised Nusselt number is close to that obtained experimentally, although the Rayleigh number that they used is much lower than the one used by He et al. (Reference He, Funfschilling, Nobach, Bodenschatz and Guenter2012). More recently, Wen, Goluskin & Doering (Reference Wen, Goluskin and Doering2022) continued the same solution branch to higher Rayleigh numbers and claimed that the maximum Nusselt number corresponds to the so-called classical scaling, where the Nusselt number is proportional to the Rayleigh number to the power of one-third (Malkus Reference Malkus1954; Priestley Reference Priestley1954; Grossmann & Lohse Reference Grossmann and Lohse2000; Kawano et al. Reference Kawano, Motoki, Shimizu and Kawahara2021). The study by Kooloth, Sondak & Smith (Reference Kooloth, Sondak and Smith2021) confirmed that roll cells with different wavelengths play important roles in two-dimensionally restricted RBC turbulence. This paper is motivated by all of the above RBC studies.
In the classical turbulence regime of TCF, where Taylor vortices are observed robustly in experiments, the symmetry restriction of the flow may not be necessary for a good agreement between the steady solution and turbulence, and at least a better agreement than in RBC can be expected. The situation is different in the ultimate turbulence regime, where eddies of different sizes and wavelengths are present, making the structure far more complex than classical turbulence. However, as long as the cylinders are not strongly counter-rotating, the experimental observations indicate that vortices of approximately the scale of the gap are still present, suggesting that Taylor vortices may play some role in the dynamics.
It should also be noted that previous theoretical studies have shown that analytical approximations can be obtained for vortices with extremely short wavelengths driven by thermal or Coriolis forces (Hall & Lakin Reference Hall and Lakin1988; Bassom & Hall Reference Bassom and Hall1989; Bassom & Blennerhassett Reference Bassom and Blennerhassett1992; Denier Reference Denier1992; Blennerhassett & Bassom Reference Blennerhassett and Bassom1994). In this type of asymptotic theory, the mean flow varies by a finite amount from the base flow and is therefore called a strongly nonlinear theory. However, the scaling of momentum and heat transport of the nonlinear state is not so different from that of the basic flow, and in this sense, the character of fully developed turbulence is not well captured. Attempts have been made to construct asymptotic solutions with larger amplitudes, but a complete understanding is still lacking. This paper proposes a solution to this long-standing problem.
In the next section, we begin by formulating our problem. Comparisons of the Taylor vortex solutions with previous experiments and simulations are then carried out in § 3. In § 4, a matched asymptotic expansion analysis is performed for the case of Taylor vortices with an aspect ratio approximately unity. We will see in § 5 that the asymptotic structure of the solution changes dramatically when the axial period becomes asymptotically short. In § 6, how the short-period vortices develop from the laminar solution is investigated in detail using a matched asymptotic expansion. Finally, in § 7, the main findings are summarised and discussed.
2. Formulation of the problem
Taylor–Couette flow can be described by the Navier–Stokes equations in the cylindrical coordinates ![]() $(r,\theta,z)$. If the flow is axisymmetric, then the governing equations are written as
$(r,\theta,z)$. If the flow is axisymmetric, then the governing equations are written as
The operators ![]() $D$ and
$D$ and ![]() $\triangle$ are defined as
$\triangle$ are defined as ![]() $D=\partial _t+u\,\partial _r+w\,\partial _z$ and
$D=\partial _t+u\,\partial _r+w\,\partial _z$ and ![]() $\triangle =\partial _r^2+r^{-1}\,\partial _r+\partial _z^2.$ The length and velocity scales are chosen so that the cylinder gap is unity, and the no-slip conditions on the cylinder walls are described as
$\triangle =\partial _r^2+r^{-1}\,\partial _r+\partial _z^2.$ The length and velocity scales are chosen so that the cylinder gap is unity, and the no-slip conditions on the cylinder walls are described as
using the Reynolds numbers associated with the rotation of the inner and outer cylinders, ![]() $R_i$ and
$R_i$ and ![]() $R_o$. Note that our non-dimensionalisation implies that using the radius ratio
$R_o$. Note that our non-dimensionalisation implies that using the radius ratio ![]() $\eta =r_i/r_o < 1$, the inner and outer radii are specified as
$\eta =r_i/r_o < 1$, the inner and outer radii are specified as
respectively. The circular Couette flow solution is written as
For other non-trivial solutions of (2.1), periodicity is imposed in the interval ![]() $z\in [0,2{\rm \pi} /k]$ using the axial wavenumber
$z\in [0,2{\rm \pi} /k]$ using the axial wavenumber ![]() $k$. The momentum equations (2.1a)–(2.1c) can be simplified as
$k$. The momentum equations (2.1a)–(2.1c) can be simplified as
using the azimuthal vorticity
and the Stokes streamfunction ![]() $\varPsi$. The roll cell velocity can be reconstructed as
$\varPsi$. The roll cell velocity can be reconstructed as ![]() $u=-r^{-1}\,\partial _z \varPsi$ and
$u=-r^{-1}\,\partial _z \varPsi$ and ![]() $w=r^{-1}\,\partial _r \varPsi$. Steady solutions of the above system can be computed without regarding their stability by using the numerical code used in our previous studies (Deguchi & Altmeyer Reference Deguchi and Altmeyer2013; Deguchi, Meseguer & Mellibovsky Reference Deguchi, Meseguer and Mellibovsky2014). The code is based on the Newton–Raphson method applied to the Chebyshev–Fourier discretised system. To calculate the Taylor vortex with aspect ratio approximately unity, we typically used up to 250th Chebyshev polynomials and 250th Fourier harmonics. This spatial resolution is more than sufficient for
$w=r^{-1}\,\partial _r \varPsi$. Steady solutions of the above system can be computed without regarding their stability by using the numerical code used in our previous studies (Deguchi & Altmeyer Reference Deguchi and Altmeyer2013; Deguchi, Meseguer & Mellibovsky Reference Deguchi, Meseguer and Mellibovsky2014). The code is based on the Newton–Raphson method applied to the Chebyshev–Fourier discretised system. To calculate the Taylor vortex with aspect ratio approximately unity, we typically used up to 250th Chebyshev polynomials and 250th Fourier harmonics. This spatial resolution is more than sufficient for ![]() $Ta=O(10^{10})$. We will see that when
$Ta=O(10^{10})$. We will see that when ![]() $k$ is large, we can reach higher Taylor numbers. In this case, the highest degree of Chebyshev polynomials was increased to 450 to fully resolve the very thin near-wall boundary layer structures.
$k$ is large, we can reach higher Taylor numbers. In this case, the highest degree of Chebyshev polynomials was increased to 450 to fully resolve the very thin near-wall boundary layer structures.
Instead of the two Reynolds numbers, the majority of high-Taylor-number TCF studies summarised in Grossmann et al. (Reference Grossmann, Lohse and Sun2016) used the Taylor number ![]() $Ta$ and the rotation rate
$Ta$ and the rotation rate ![]() $a$. These are easily found by the standard parameters as
$a$. These are easily found by the standard parameters as
The former parameter is similar to the shear Reynolds number used in Dubrulle et al. (Reference Dubrulle, Dauchot, Daviaud, Longgaretti, Richard and Zahn2005), and is zero for the rigid body rotation case. (Their second parameter, the rotation number, is a function of ![]() $a$ and
$a$ and ![]() $\eta$.)
$\eta$.)
The Nusselt number is defined by
where
is the mean azimuthal velocity.
In the limit ![]() $\eta \rightarrow 1$, the gap becomes much narrower than the cylinder radius, and the local flow can be represented in Cartesian coordinates. As noted by Deguchi (Reference Deguchi2016), there are several variations on the narrow gap limit, two of which are relevant to this paper. One is of course the rotating plane Couette flow, where the system is in perfect agreement with RBC if the Prandtl number is unity (see e.g. Chandrasekhar Reference Chandrasekhar1961; Robinson Reference Robinson1967; Veronis Reference Veronis1970; Lezius & Johnston Reference Lezius and Johnston1976; Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2017). The other variation utilises an argument similar to the derivation of the Görtler vortex (Hall Reference Hall1983), and is used, for example, by Denier (Reference Denier1992). For completeness, the difference between the two limits is highlighted in Appendix A.
$\eta \rightarrow 1$, the gap becomes much narrower than the cylinder radius, and the local flow can be represented in Cartesian coordinates. As noted by Deguchi (Reference Deguchi2016), there are several variations on the narrow gap limit, two of which are relevant to this paper. One is of course the rotating plane Couette flow, where the system is in perfect agreement with RBC if the Prandtl number is unity (see e.g. Chandrasekhar Reference Chandrasekhar1961; Robinson Reference Robinson1967; Veronis Reference Veronis1970; Lezius & Johnston Reference Lezius and Johnston1976; Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2017). The other variation utilises an argument similar to the derivation of the Görtler vortex (Hall Reference Hall1983), and is used, for example, by Denier (Reference Denier1992). For completeness, the difference between the two limits is highlighted in Appendix A.
3. Comparison of the steady solutions and the experiments
Here, we use the radius ratio ![]() $\eta =5/7$ and fix the outer cylinder (
$\eta =5/7$ and fix the outer cylinder (![]() $a=0$) to compute the Taylor vortex solutions. Significant deviations from the narrow gap approximation can be observed at this radius ratio. That parameter choice is frequently used in experiments and numerical simulations (see § 3 of Grossmann et al. Reference Grossmann, Lohse and Sun2016), and is hence convenient for the comparison. The red curve in figure 1 shows the Taylor vortex solution calculated with the fixed axial wavenumber
$a=0$) to compute the Taylor vortex solutions. Significant deviations from the narrow gap approximation can be observed at this radius ratio. That parameter choice is frequently used in experiments and numerical simulations (see § 3 of Grossmann et al. Reference Grossmann, Lohse and Sun2016), and is hence convenient for the comparison. The red curve in figure 1 shows the Taylor vortex solution calculated with the fixed axial wavenumber ![]() $k$. According to the simulations, the Taylor cells are relatively robust even in the numerically generated classical turbulent flows, with cell aspect ratio approximately unity. More specifically, direct numerical simulations (DNS) by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) imposed the axial periodicity
$k$. According to the simulations, the Taylor cells are relatively robust even in the numerically generated classical turbulent flows, with cell aspect ratio approximately unity. More specifically, direct numerical simulations (DNS) by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) imposed the axial periodicity ![]() $2{\rm \pi}$ and typically observed three vortex pairs (i.e.
$2{\rm \pi}$ and typically observed three vortex pairs (i.e. ![]() $k=3$ modes). This motivated the choice of
$k=3$ modes). This motivated the choice of ![]() $k=3$ for our Taylor vortex computation.
$k=3$ for our Taylor vortex computation.

Figure 1. The variation of Nusselt number ![]() $Nu$ with respect to Taylor number
$Nu$ with respect to Taylor number ![]() $Ta$. The outer cylinder is fixed (
$Ta$. The outer cylinder is fixed (![]() $a=0$), and
$a=0$), and ![]() $\eta =5/7\approx 0.714$. The red solid curve is the Taylor vortex solution branch with the fixed wavenumber
$\eta =5/7\approx 0.714$. The red solid curve is the Taylor vortex solution branch with the fixed wavenumber ![]() $k=3$. The red crosses are the same solutions, but the wavenumber is optimised to maximise
$k=3$. The red crosses are the same solutions, but the wavenumber is optimised to maximise ![]() $Nu$. The blue circles are the three-dimensional direct numerical simulations by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a). The green triangles and squares are the experiments by Lewis & Swinney (Reference Lewis and Swinney1999) and Dennis et al. (Reference Dennis, Huisman, Bruggert, Sun and Lohse2011), respectively. The simulation and experimental results are time-averaged data. The best theoretical upper bound known to date has the asymptotic form
$Nu$. The blue circles are the three-dimensional direct numerical simulations by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a). The green triangles and squares are the experiments by Lewis & Swinney (Reference Lewis and Swinney1999) and Dennis et al. (Reference Dennis, Huisman, Bruggert, Sun and Lohse2011), respectively. The simulation and experimental results are time-averaged data. The best theoretical upper bound known to date has the asymptotic form ![]() $Nu=0.0075\,Ta^{1/2}$ according to Ding & Marensi (Reference Ding and Marensi2019).
$Nu=0.0075\,Ta^{1/2}$ according to Ding & Marensi (Reference Ding and Marensi2019).
The solution branch bifurcates from the circular Couette flow at ![]() $Ta\approx 10^4$, and as the Taylor number increases, it loses stability with respect to three-dimensional perturbations. The onset of turbulence is at
$Ta\approx 10^4$, and as the Taylor number increases, it loses stability with respect to three-dimensional perturbations. The onset of turbulence is at ![]() $Ta\approx 3\times 10^6$. The blue circles in figure 1 are the DNS by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a). Despite the relatively short axial periodicity imposed, the simulations are known to agree reasonably with the experimental results (the squares and triangles in figure 1). One may be concerned about the impact of endwalls in this comparison as it is known to alter the detailed structure of the bifurcation near the onset of Taylor vortices (Czarny, Serre & Bontoux Reference Czarny, Serre and Bontoux2003). To address this concern, van Gils et al. (Reference van Gils, Huisman, Grossmann, Sun and Lohse2012) conducted thorough experimental observations and concluded that if the height of the cylinders is sufficient and the flow is measured near the mid-height, then the effects of the endwalls can be negligible. The key point of their conclusion is that their flow is subjected to strong centrifugal instability, hence vortices with relatively short wavelengths play a major role in the angular momentum transport. This flow characteristic is quite different from centrifugally stable high-Reynolds-number flows, where the angular momentum transport is strongly influenced by endwall design (Avila et al. Reference Avila, Grimes, Lopez and Marques2008; Avila Reference Avila2012).
$Ta\approx 3\times 10^6$. The blue circles in figure 1 are the DNS by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) and Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a). Despite the relatively short axial periodicity imposed, the simulations are known to agree reasonably with the experimental results (the squares and triangles in figure 1). One may be concerned about the impact of endwalls in this comparison as it is known to alter the detailed structure of the bifurcation near the onset of Taylor vortices (Czarny, Serre & Bontoux Reference Czarny, Serre and Bontoux2003). To address this concern, van Gils et al. (Reference van Gils, Huisman, Grossmann, Sun and Lohse2012) conducted thorough experimental observations and concluded that if the height of the cylinders is sufficient and the flow is measured near the mid-height, then the effects of the endwalls can be negligible. The key point of their conclusion is that their flow is subjected to strong centrifugal instability, hence vortices with relatively short wavelengths play a major role in the angular momentum transport. This flow characteristic is quite different from centrifugally stable high-Reynolds-number flows, where the angular momentum transport is strongly influenced by endwall design (Avila et al. Reference Avila, Grimes, Lopez and Marques2008; Avila Reference Avila2012).
Both the experiments and simulations indicate the existence of a transition point ![]() $Ta\approx 10^8$ at which the behaviour of
$Ta\approx 10^8$ at which the behaviour of ![]() $Nu$ changes. The turbulence below/above the transition point is referred to as the classical/ultimate regime. The Nusselt number of the ultimate turbulence has the scaling
$Nu$ changes. The turbulence below/above the transition point is referred to as the classical/ultimate regime. The Nusselt number of the ultimate turbulence has the scaling ![]() $Nu\propto Ta^{\beta }$ with the exponent
$Nu\propto Ta^{\beta }$ with the exponent ![]() $\beta \approx 0.38$, which is also seen in the RBC experiments (He et al. Reference He, Funfschilling, Nobach, Bodenschatz and Guenter2012). The empirical asymptotic prediction
$\beta \approx 0.38$, which is also seen in the RBC experiments (He et al. Reference He, Funfschilling, Nobach, Bodenschatz and Guenter2012). The empirical asymptotic prediction ![]() ${Nu=0.009\,Ta^{0.38}}$ sits well below the theoretical upper bound of
${Nu=0.009\,Ta^{0.38}}$ sits well below the theoretical upper bound of ![]() $Nu$ derived by Ding & Marensi (Reference Ding and Marensi2019). The exponent
$Nu$ derived by Ding & Marensi (Reference Ding and Marensi2019). The exponent ![]() $1/2$ is typical for upper bounds using the energy method. Similar asymptotic behaviour of
$1/2$ is typical for upper bounds using the energy method. Similar asymptotic behaviour of ![]() $Nu$ but with a logarithmic correction has been proposed using the phenomenology of the log law of turbulent boundary layers (see Grossmann et al. Reference Grossmann, Lohse and Sun2016). It is, however, not known whether such scaling can be observed clearly in experiments.
$Nu$ but with a logarithmic correction has been proposed using the phenomenology of the log law of turbulent boundary layers (see Grossmann et al. Reference Grossmann, Lohse and Sun2016). It is, however, not known whether such scaling can be observed clearly in experiments.
As long as the solution has aspect ratio approximately unity, it captures the nature of classical turbulence surprisingly well. This is best illustrated by a comparison of mean flows shown in figure 2(a). Here,
is the shifted and normalised mean angular velocity (denoted by ![]() $\langle \bar {\omega }\rangle _z$ in Ostilla et al. Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013). At sufficiently high Taylor numbers, the boundary layer formation near the cylinder walls is clearly visible. As seen in figure 1, the solution gives a reasonable estimate of
$\langle \bar {\omega }\rangle _z$ in Ostilla et al. Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013). At sufficiently high Taylor numbers, the boundary layer formation near the cylinder walls is clearly visible. As seen in figure 1, the solution gives a reasonable estimate of ![]() $Nu$ in the classical turbulence regime. The cross-section of the Taylor vortex (see figure 3b) reveals that the boundary layer actually surrounds the vortex core, where the azimuthal velocity appears to be rather uniform. The dynamics of the boundary layers in the classical turbulence is known to be somewhat quiescent (see e.g. Ostilla et al. Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013), and their qualitative structure is reminiscent of figure 3(b). The literature summarised in Grossmann et al. (Reference Grossmann, Lohse and Sun2016) often implies that the Prandtl–Blasius theory could be applied to the boundary layer, and we will see in § 4 that this is, in fact, true for the asymptotic limit of the steady solution. Moreover, the theory to be presented in § 4 yields the scaling of
$Nu$ in the classical turbulence regime. The cross-section of the Taylor vortex (see figure 3b) reveals that the boundary layer actually surrounds the vortex core, where the azimuthal velocity appears to be rather uniform. The dynamics of the boundary layers in the classical turbulence is known to be somewhat quiescent (see e.g. Ostilla et al. Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013), and their qualitative structure is reminiscent of figure 3(b). The literature summarised in Grossmann et al. (Reference Grossmann, Lohse and Sun2016) often implies that the Prandtl–Blasius theory could be applied to the boundary layer, and we will see in § 4 that this is, in fact, true for the asymptotic limit of the steady solution. Moreover, the theory to be presented in § 4 yields the scaling of ![]() $Nu \propto Ta^{0.25}$ and
$Nu \propto Ta^{0.25}$ and ![]() $Re_w \propto Ta^{0.5}$, which agree well with the turbulent observations. Here,
$Re_w \propto Ta^{0.5}$, which agree well with the turbulent observations. Here, ![]() $Re_w$ is the wind Reynolds number, i.e. the typical roll cell circulation speed normalised by the viscous velocity scale
$Re_w$ is the wind Reynolds number, i.e. the typical roll cell circulation speed normalised by the viscous velocity scale ![]() $\nu /d$ (where
$\nu /d$ (where ![]() $\nu$ is the kinematic viscosity of the fluid, and
$\nu$ is the kinematic viscosity of the fluid, and ![]() $d$ is the cylinder gap). The precise definition of the wind Reynolds number varies in the literature. Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) measured the standard deviation of the radial velocity
$d$ is the cylinder gap). The precise definition of the wind Reynolds number varies in the literature. Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) measured the standard deviation of the radial velocity ![]() $u$, while Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) computed the average of
$u$, while Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013) computed the average of ![]() $u^2+w^2$ and then square-rooted it. Both definitions give the same scaling, but with different prefactors.
$u^2+w^2$ and then square-rooted it. Both definitions give the same scaling, but with different prefactors.

Figure 2. The mean angular velocity ![]() $q$ defined in (3.1) for
$q$ defined in (3.1) for ![]() $\eta =5/7$,
$\eta =5/7$, ![]() $a=0$. (a) The classical turbulence regime
$a=0$. (a) The classical turbulence regime ![]() $Ta=9.52\times 10^6$. The red solid curve is the Taylor vortex solution. The blue dot-dashed curve is the time-averaged DNS result by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013). (b) The ultimate turbulence regime. The blue dot-dashed curve is the time-averaged DNS result by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b) (
$Ta=9.52\times 10^6$. The red solid curve is the Taylor vortex solution. The blue dot-dashed curve is the time-averaged DNS result by Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013). (b) The ultimate turbulence regime. The blue dot-dashed curve is the time-averaged DNS result by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b) (![]() $Ta=10^{10}$). The other curves are the Taylor vortex solutions shown in figures 3(b–d) (
$Ta=10^{10}$). The other curves are the Taylor vortex solutions shown in figures 3(b–d) (![]() $Ta=9.75\times 10^9$).
$Ta=9.75\times 10^9$).

Figure 3. Axial wavenumber dependence of the Taylor vortex solutions. The parameters are ![]() $\eta =5/7$,
$\eta =5/7$, ![]() $R_i=8\times 10^4$,
$R_i=8\times 10^4$, ![]() $R_o=0$, which correspond to
$R_o=0$, which correspond to ![]() $Ta=9.75\times 10^9$ in figure 1. (a) The bifurcation diagram. The blue dotted curve is the Taylor vortex solution branch. This branch bifurcates from the linear critical point
$Ta=9.75\times 10^9$ in figure 1. (a) The bifurcation diagram. The blue dotted curve is the Taylor vortex solution branch. This branch bifurcates from the linear critical point ![]() $L$ of the circular Couette flow. There is another linear critical point at very small
$L$ of the circular Couette flow. There is another linear critical point at very small ![]() $k$, but computing the bifurcating solution branch at this Taylor number is difficult, hence it is omitted. (b–d) Azimuthal velocity
$k$, but computing the bifurcating solution branch at this Taylor number is difficult, hence it is omitted. (b–d) Azimuthal velocity ![]() $v$ at the selected points in (a). The colour bar range is
$v$ at the selected points in (a). The colour bar range is ![]() $[0,80\,000]$. All the solutions possess reflectional symmetry in
$[0,80\,000]$. All the solutions possess reflectional symmetry in ![]() $z$. (e, f) Enlarged views of parts of (c,d), respectively. The colour bar range is changed to
$z$. (e, f) Enlarged views of parts of (c,d), respectively. The colour bar range is changed to ![]() $[10\,000,70\,000]$ in the enlarged figures.
$[10\,000,70\,000]$ in the enlarged figures.
In the ultimate turbulence, on the other hand, the situation appears to be more intricate. The snapshots of turbulence are typically accompanied by eddies of a vast scale, whereby the large-scale Taylor vortex is blurred in the time-averaged field. In particular, small turbulent eddies appearing in the boundary layer have been pointed out as a critical qualitative difference between the two turbulent regimes separated by the transition point seen in figure 1 (Dong Reference Dong2007; Ostilla-Mónico et al. Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014a). Therefore, solutions with larger wavenumbers may play a more critical role in the turbulent dynamics. Our Nusselt number results also support this speculation. As seen in figure 1, the Taylor vortex with fixed ![]() $k$ underestimates experimental
$k$ underestimates experimental ![]() $Nu$ in the ultimate regime. However, if
$Nu$ in the ultimate regime. However, if ![]() $k$ is optimised to maximise
$k$ is optimised to maximise ![]() $Nu$ (the crosses in figure 1), then it can reach the experimental values for
$Nu$ (the crosses in figure 1), then it can reach the experimental values for ![]() $Ta \lesssim 10^{11}$.
$Ta \lesssim 10^{11}$.
Figure 3(a) shows how ![]() $Nu$ changes as the wavenumber
$Nu$ changes as the wavenumber ![]() $k$ of the Taylor vortex is varied. The
$k$ of the Taylor vortex is varied. The ![]() $Nu$ curve has two local maxima. The bimodal distribution of
$Nu$ curve has two local maxima. The bimodal distribution of ![]() $Nu$ and the scaling of the two peaks are remarkably similar to those seen in the RBC roll cell computation by Waleffe et al. (Reference Waleffe, Boonkasame and Smith2015) and Sondak et al. (Reference Sondak, Smith and Waleffe2015). Based on their calculations at several Rayleigh numbers
$Nu$ and the scaling of the two peaks are remarkably similar to those seen in the RBC roll cell computation by Waleffe et al. (Reference Waleffe, Boonkasame and Smith2015) and Sondak et al. (Reference Sondak, Smith and Waleffe2015). Based on their calculations at several Rayleigh numbers ![]() $Ra$, the first (second) peak has the wavenumber scaling
$Ra$, the first (second) peak has the wavenumber scaling ![]() $k\propto Ra^{0.217}$ (
$k\propto Ra^{0.217}$ (![]() $Ra^{0.256}$) with the Nusselt number scaling exponent
$Ra^{0.256}$) with the Nusselt number scaling exponent ![]() $\beta$ slightly larger (smaller) than 0.31. We will provide a theoretical rationale for the scaling in §§ 5 and 6.
$\beta$ slightly larger (smaller) than 0.31. We will provide a theoretical rationale for the scaling in §§ 5 and 6.
For the ultimate turbulence regime, the approximation of the turbulent mean flow by the ![]() $k=3$ state is slightly worse (figure 2b). However, the mean flow of course varies with
$k=3$ state is slightly worse (figure 2b). However, the mean flow of course varies with ![]() $k$. As the value of
$k$. As the value of ![]() $k$ is increased from 3, the mean flow of the solution in the core region approaches a turbulent profile in the vicinity of the second peak. Figures 3(c) and 3(d) show the flow field at each peak, which is also examined in detail in the following two sections.
$k$ is increased from 3, the mean flow of the solution in the core region approaches a turbulent profile in the vicinity of the second peak. Figures 3(c) and 3(d) show the flow field at each peak, which is also examined in detail in the following two sections.
4. Taylor vortices with an  $O(1)$ cell aspect ratio
$O(1)$ cell aspect ratio
In figure 2(a), we saw that some kind of homogenisation occurs in the core region of the Taylor vortex, and a thin boundary layer emerges around it. Such a flow structure looks very much like the high-Rayleigh-number RBC roll cell, which was studied intensively from the 1950s to the 1970s, for example, by Pillow (Reference Pillow1952), Robinson (Reference Robinson1967) and Wesseling (Reference Wesseling1969). More recently, it was reported that when the slip walls are imposed, the asymptotic solution can be calculated semi-analytically and is in good agreement with the numerical solutions (Chini & Cox Reference Chini and Cox2009; Hepworth Reference Hepworth2014). However, as noted by Robinson (Reference Robinson1967), for no-slip walls, the scaling and structure of the boundary layer have to be modified, which makes analytical progress difficult. The situation in the Taylor vortex is close to the latter problem, as we will see below.
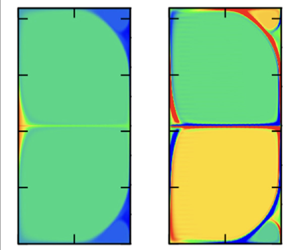
First, let us examine the core region. For RBC, the roll cell vorticity in this region is known to become constant due to the Prandtl–Batchelor theorem, which states that the homogenisation of the vorticity occurs in the region where the streamlines are closed in two-dimensional inviscid flows (Prandtl Reference Prandtl1904; Batchelor Reference Batchelor1956; Feynman & Lagerstrom Reference Feynman and Lagerstrom1956). Moreover, the temperature becomes constant as well because the temperature equation has a structure similar to that of the vorticity equation (see e.g. Moore & Weiss Reference Moore and Weiss1973). To better see what precise physical quantities are homogenised in the core of the Taylor vortex, it is desirable to choose large gaps. Figure 4 shows the results for ![]() $\eta =0.5$. The colour map shown in figure 4(b) indicates clearly that it is actually angular momentum
$\eta =0.5$. The colour map shown in figure 4(b) indicates clearly that it is actually angular momentum ![]() $rv$ that becomes uniform in the region where the streamlines are closed. Also, figure 4(c) shows that it is not the azimuthal vorticity
$rv$ that becomes uniform in the region where the streamlines are closed. Also, figure 4(c) shows that it is not the azimuthal vorticity ![]() $\omega$ that homogenises, but
$\omega$ that homogenises, but ![]() $\omega /r$.
$\omega /r$.

Figure 4. The flow field of the Taylor vortex for ![]() $\eta =0.5$,
$\eta =0.5$, ![]() $k=3$. The Reynolds numbers used are
$k=3$. The Reynolds numbers used are ![]() $R_i=8\times 10^4$,
$R_i=8\times 10^4$, ![]() $R_o=0.25 R_i$, corresponding to
$R_o=0.25 R_i$, corresponding to ![]() $Ta=1.40\times 10^{10}$,
$Ta=1.40\times 10^{10}$, ![]() $a=-1/8$. (a) The Stokes streamfunction
$a=-1/8$. (a) The Stokes streamfunction ![]() $\varPsi$. The colour bar range is
$\varPsi$. The colour bar range is ![]() $[-7500,7500]$. (b) The angular momentum
$[-7500,7500]$. (b) The angular momentum ![]() $rv$. The colour bar range is
$rv$. The colour bar range is ![]() $[40\,000,80\,000]$. (c) The modified azimuthal vorticity
$[40\,000,80\,000]$. (c) The modified azimuthal vorticity ![]() $\omega /r$. The colour bar range is
$\omega /r$. The colour bar range is ![]() $[-120\,000,120\,000]$. This quantity is distributed uniformly in the core to a value of approximately
$[-120\,000,120\,000]$. This quantity is distributed uniformly in the core to a value of approximately ![]() $\pm 37$ % of the colour bar.
$\pm 37$ % of the colour bar.
Building on the above observations, now we introduce the new variables ![]() $\varGamma =Ta^{-1/2}\,rv$ and
$\varGamma =Ta^{-1/2}\,rv$ and ![]() $\varOmega =\omega /r$, whereby the governing equations (2.6) are rewritten as
$\varOmega =\omega /r$, whereby the governing equations (2.6) are rewritten as
Here, the subscript ![]() $r$ or
$r$ or ![]() $z$ denotes a partial differentiation. The no-slip conditions become
$z$ denotes a partial differentiation. The no-slip conditions become
If ![]() $\varGamma$ is considered as temperature,
$\varGamma$ is considered as temperature, ![]() $\varOmega$ as roll cell vorticity and
$\varOmega$ as roll cell vorticity and ![]() $Ta$ as Rayleigh number, then one may notice that the structure of the equations is very similar to that of the two-dimensional RBC. The last term in the right-hand side of (4.1b) corresponds to the Coriolis force when the rotating plane Couette flow (RPCF) limit is taken, and it plays a role of buoyancy. (This term is not exactly the Coriolis force unless the system is in the RPCF limit, but for simplicity we will call it ‘Coriolis force’ hereafter; see Appendix A also.) This analogy in the sense of the structure of the equations would explain why
$Ta$ as Rayleigh number, then one may notice that the structure of the equations is very similar to that of the two-dimensional RBC. The last term in the right-hand side of (4.1b) corresponds to the Coriolis force when the rotating plane Couette flow (RPCF) limit is taken, and it plays a role of buoyancy. (This term is not exactly the Coriolis force unless the system is in the RPCF limit, but for simplicity we will call it ‘Coriolis force’ hereafter; see Appendix A also.) This analogy in the sense of the structure of the equations would explain why ![]() $\varGamma$ and
$\varGamma$ and ![]() $\varOmega$ become constant in the Taylor vortex core, as seen in figure 4, at least on an intuitive level.
$\varOmega$ become constant in the Taylor vortex core, as seen in figure 4, at least on an intuitive level.
In fact, following Batchelor (Reference Batchelor1956), a mathematical argument can be developed. First, assuming that the typical roll cell circulation strength ![]() $Re_w$ (the wind Reynolds number) is asymptotically large, we expand
$Re_w$ (the wind Reynolds number) is asymptotically large, we expand ![]() $\varPsi =Re_w\,\varPsi _0+\cdots$,
$\varPsi =Re_w\,\varPsi _0+\cdots$, ![]() $\varGamma =\varGamma _0+\cdots$ and
$\varGamma =\varGamma _0+\cdots$ and ![]() $\varOmega =Re_w\,\varOmega _0+\cdots$. Then the leading-order part of (4.1a) becomes
$\varOmega =Re_w\,\varOmega _0+\cdots$. Then the leading-order part of (4.1a) becomes ![]() $\varPsi _{0r} \varGamma _{0z}-\varPsi _{0z} \varGamma _{0r}=0$, which suggests that the function
$\varPsi _{0r} \varGamma _{0z}-\varPsi _{0z} \varGamma _{0r}=0$, which suggests that the function ![]() $\varGamma _0$ depends only on
$\varGamma _0$ depends only on ![]() $\varPsi _0$. Now, in the
$\varPsi _0$. Now, in the ![]() $r$–
$r$–![]() $z$ plane, take a region
$z$ plane, take a region ![]() $\mathcal {A}$ enclosed by a streamline
$\mathcal {A}$ enclosed by a streamline ![]() $\mathcal {C}$ oriented counterclockwise (thus
$\mathcal {C}$ oriented counterclockwise (thus ![]() $\varPsi$ is constant along
$\varPsi$ is constant along ![]() $\mathcal {C}$). Integrating (4.1a) over
$\mathcal {C}$). Integrating (4.1a) over ![]() $\mathcal {A}$, we obtain
$\mathcal {A}$, we obtain
The left-hand side vanishes because upon using the Stokes theorem it becomes
The second equality comes from the fact that the gradient of ![]() $\varPsi$ and the line element on
$\varPsi$ and the line element on ![]() $\mathcal {C}$,
$\mathcal {C}$, ![]() ${\rm d}\boldsymbol {l}$, are orthogonal on the streamline. Meanwhile the leading-order part of the right-hand side can be transformed by again applying the Stokes theorem:
${\rm d}\boldsymbol {l}$, are orthogonal on the streamline. Meanwhile the leading-order part of the right-hand side can be transformed by again applying the Stokes theorem:
 \begin{align} 0&=\oint_{\mathcal{C}} r^3\{(r^{{-}2}\varGamma_0)_r\boldsymbol{e}_z-(r^{{-}2}\varGamma_0)_z\boldsymbol{e}_r\} \boldsymbol{\cdot} {\rm d}\boldsymbol{l} \nonumber\\ &=\frac{{\rm d}\varGamma_{0}}{{\rm d}\varPsi_0}\oint_{\mathcal{C}} r^2\{r^{{-}1}\varPsi_{0r}\boldsymbol{e}_z-r^{{-}1}\varPsi_{0z}\boldsymbol{e}_r\} \boldsymbol{\cdot} {\rm d}\boldsymbol{l} -2 \varGamma_0 \oint_{\mathcal{C}} \boldsymbol{e}_z \boldsymbol{\cdot} {\rm d}\boldsymbol{l} \nonumber\\ &=\frac{{\rm d}\varGamma_{0}}{{\rm d}\varPsi_0}\oint_{\mathcal{C}} r^2\{u_0\boldsymbol{e}_r+w_0\boldsymbol{e}_z\}\boldsymbol{\cdot} {\rm d}\boldsymbol{l}. \end{align}
\begin{align} 0&=\oint_{\mathcal{C}} r^3\{(r^{{-}2}\varGamma_0)_r\boldsymbol{e}_z-(r^{{-}2}\varGamma_0)_z\boldsymbol{e}_r\} \boldsymbol{\cdot} {\rm d}\boldsymbol{l} \nonumber\\ &=\frac{{\rm d}\varGamma_{0}}{{\rm d}\varPsi_0}\oint_{\mathcal{C}} r^2\{r^{{-}1}\varPsi_{0r}\boldsymbol{e}_z-r^{{-}1}\varPsi_{0z}\boldsymbol{e}_r\} \boldsymbol{\cdot} {\rm d}\boldsymbol{l} -2 \varGamma_0 \oint_{\mathcal{C}} \boldsymbol{e}_z \boldsymbol{\cdot} {\rm d}\boldsymbol{l} \nonumber\\ &=\frac{{\rm d}\varGamma_{0}}{{\rm d}\varPsi_0}\oint_{\mathcal{C}} r^2\{u_0\boldsymbol{e}_r+w_0\boldsymbol{e}_z\}\boldsymbol{\cdot} {\rm d}\boldsymbol{l}. \end{align}
Here, ![]() $(u_0, w_0)=(-r^{-1}\varPsi _{0z},r^{-1}\varPsi _{0r})$ is the leading-order part of the roll velocity. The integral in the last line should not vanish because we are assuming the existence of a strong circulation due to the swirling motion of the Taylor roll. Thus the equation implies
$(u_0, w_0)=(-r^{-1}\varPsi _{0z},r^{-1}\varPsi _{0r})$ is the leading-order part of the roll velocity. The integral in the last line should not vanish because we are assuming the existence of a strong circulation due to the swirling motion of the Taylor roll. Thus the equation implies ![]() ${{\rm d}\varGamma _{0}}/{{\rm d}\varPsi _0}=0$ at the value of
${{\rm d}\varGamma _{0}}/{{\rm d}\varPsi _0}=0$ at the value of ![]() $\varPsi _0$ on
$\varPsi _0$ on ![]() ${\mathcal {C}}$ that we choose. The above argument holds for any region enclosed by a streamline, hence the value of
${\mathcal {C}}$ that we choose. The above argument holds for any region enclosed by a streamline, hence the value of ![]() $\varGamma _0$ must be constant in the core region. The argument above does not change when an arbitrary constant is added to
$\varGamma _0$ must be constant in the core region. The argument above does not change when an arbitrary constant is added to ![]() $\varGamma$. This implies that if power series asymptotic expansion of
$\varGamma$. This implies that if power series asymptotic expansion of ![]() $\varGamma$ is considered, then the homogenisation also occurs in all the higher-order terms as long as they have a spatial scale of
$\varGamma$ is considered, then the homogenisation also occurs in all the higher-order terms as long as they have a spatial scale of ![]() $O(1)$. Therefore, for steady solutions, the non-uniform component in
$O(1)$. Therefore, for steady solutions, the non-uniform component in ![]() $\varGamma$ is exponentially small.
$\varGamma$ is exponentially small.
Likewise, we can show that the value of ![]() $\varOmega _0$ is constant as well in the core. Integrating (4.1b) over
$\varOmega _0$ is constant as well in the core. Integrating (4.1b) over ![]() ${\mathcal {A}}$ gives
${\mathcal {A}}$ gives
 \begin{align} \int_\mathcal{A} \{\varPsi_r \varOmega_z - \varPsi_z \varOmega_r \} \,{\rm d}r\,{\rm d}z &=\int_\mathcal{A} \{(r^{{-}1}(r^2\varOmega)_r)_r+(r^{{-}1}(r^2\varOmega)_{z})_z\}\,{\rm d}r\,{\rm d}z \nonumber\\ &\quad +\int_\mathcal{A} Ta\,\frac{2\varGamma \varGamma_z}{r^3} \,{\rm d}r \,{\rm d}z, \end{align}
\begin{align} \int_\mathcal{A} \{\varPsi_r \varOmega_z - \varPsi_z \varOmega_r \} \,{\rm d}r\,{\rm d}z &=\int_\mathcal{A} \{(r^{{-}1}(r^2\varOmega)_r)_r+(r^{{-}1}(r^2\varOmega)_{z})_z\}\,{\rm d}r\,{\rm d}z \nonumber\\ &\quad +\int_\mathcal{A} Ta\,\frac{2\varGamma \varGamma_z}{r^3} \,{\rm d}r \,{\rm d}z, \end{align}
and of course the left-hand side should vanish. Since we already know that ![]() $\varGamma _0$ is a constant plus an exponentially small fluctuation, the last term in the right-hand side of (4.6) can be neglected. From (4.1b), we see that
$\varGamma _0$ is a constant plus an exponentially small fluctuation, the last term in the right-hand side of (4.6) can be neglected. From (4.1b), we see that ![]() $\varOmega _0$ is a function of
$\varOmega _0$ is a function of ![]() $\varPsi _0$, thus the leading-order part of integral (4.6),
$\varPsi _0$, thus the leading-order part of integral (4.6),
 \begin{align} 0&=\oint_{\mathcal{C}} r^{{-}1}\{(r^2\varOmega_0)_r\boldsymbol{e}_z-(r^2\varOmega_0)_{z}\boldsymbol{e}_r)\}\boldsymbol{\cdot} {\rm d}\boldsymbol{l} \nonumber\\ &=\frac{{\rm d}\varOmega_{0}}{{\rm d}\varPsi_0} \oint_{\mathcal{C}} r^2\{r^{{-}1}\varPsi_{0r} \boldsymbol{e}_z-r^{{-}1}\varPsi_{0z}\boldsymbol{e}_r\}\boldsymbol{\cdot} {\rm d}\boldsymbol{l}+2\varOmega_0 \oint_{\mathcal{C}} \boldsymbol{e}_z \boldsymbol{\cdot} {\rm d}\boldsymbol{l} \nonumber\\ &=\frac{{\rm d}\varOmega_{0}}{{\rm d}\varPsi_0}\oint_{\mathcal{C}} r^2\{u_0\boldsymbol{e}_r+w_0\boldsymbol{e}_z\}\boldsymbol{\cdot} {\rm d}\boldsymbol{l}, \end{align}
\begin{align} 0&=\oint_{\mathcal{C}} r^{{-}1}\{(r^2\varOmega_0)_r\boldsymbol{e}_z-(r^2\varOmega_0)_{z}\boldsymbol{e}_r)\}\boldsymbol{\cdot} {\rm d}\boldsymbol{l} \nonumber\\ &=\frac{{\rm d}\varOmega_{0}}{{\rm d}\varPsi_0} \oint_{\mathcal{C}} r^2\{r^{{-}1}\varPsi_{0r} \boldsymbol{e}_z-r^{{-}1}\varPsi_{0z}\boldsymbol{e}_r\}\boldsymbol{\cdot} {\rm d}\boldsymbol{l}+2\varOmega_0 \oint_{\mathcal{C}} \boldsymbol{e}_z \boldsymbol{\cdot} {\rm d}\boldsymbol{l} \nonumber\\ &=\frac{{\rm d}\varOmega_{0}}{{\rm d}\varPsi_0}\oint_{\mathcal{C}} r^2\{u_0\boldsymbol{e}_r+w_0\boldsymbol{e}_z\}\boldsymbol{\cdot} {\rm d}\boldsymbol{l}, \end{align}
yields ![]() ${{\rm d}\varOmega _{0}}/{{\rm d}\varPsi _0}=0$.
${{\rm d}\varOmega _{0}}/{{\rm d}\varPsi _0}=0$.
In the above argument, we have assumed that the swirling speed of the rolls is sufficiently large, but to see exactly how large it is, we need to analyse the boundary layer. Let us now take the region ![]() $\mathcal {A}$ as large as possible, and assume that a viscous boundary layer appears around its boundary
$\mathcal {A}$ as large as possible, and assume that a viscous boundary layer appears around its boundary ![]() $\mathcal {C}$. In this core region (see figure 5a), we have the estimation
$\mathcal {C}$. In this core region (see figure 5a), we have the estimation ![]() $Re_w=O(\varPsi |_c)= O(\varOmega |_c)$, where the subscript
$Re_w=O(\varPsi |_c)= O(\varOmega |_c)$, where the subscript ![]() $c$ indicates that the physical quantities are measured in the core. At the roll cell perimeter
$c$ indicates that the physical quantities are measured in the core. At the roll cell perimeter ![]() $\mathcal {C}$, without loss of generality, we can set
$\mathcal {C}$, without loss of generality, we can set ![]() $\varPsi =0$. Hence if the thickness of the boundary layer is written as
$\varPsi =0$. Hence if the thickness of the boundary layer is written as ![]() $\epsilon$, then the size of the streamfunction there can be estimated as
$\epsilon$, then the size of the streamfunction there can be estimated as ![]() $O(\varPsi |_b)= O(\epsilon \varPsi |_c)=O(\epsilon Re_w)$ (where the subscript
$O(\varPsi |_b)= O(\epsilon \varPsi |_c)=O(\epsilon Re_w)$ (where the subscript ![]() $b$ stands for boundary layer). In order to ensure the viscous-convective balance of (4.1b) in this thin layer, we further require
$b$ stands for boundary layer). In order to ensure the viscous-convective balance of (4.1b) in this thin layer, we further require ![]() $O(\varPsi |_b)=O(\epsilon ^{-1})$, and therefore
$O(\varPsi |_b)=O(\epsilon ^{-1})$, and therefore ![]() $Re_w=O(\epsilon ^{-2})$.
$Re_w=O(\epsilon ^{-2})$.

Figure 5. Sketch of the asymptotic states. In the blue shaded region, viscosity is not negligible. In the dotted region, Coriolis force is at work. (a) Taylor vortex with aspect ratio of order unity (![]() $k=O(1)$). (b,c) The first peak state (
$k=O(1)$). (b,c) The first peak state (![]() $k=O(Ta^{2/9})$), where (b) is the close-up of the near-wall zone enclosed by the red lines in (c).
$k=O(Ta^{2/9})$), where (b) is the close-up of the near-wall zone enclosed by the red lines in (c).
As seen in figure 4(c), parts of the boundary layer are attached to the walls, where the flow has to fulfil the no-slip conditions. In order for the streamfunction to be modified in the near-wall boundary layer, both sides of (4.1c) must balance, so ![]() $O(\varOmega |_b)=O(\epsilon ^{-1}\,Re_w)$ using
$O(\varOmega |_b)=O(\epsilon ^{-1}\,Re_w)$ using ![]() $\partial _r=O(\epsilon ^{-1})$ and
$\partial _r=O(\epsilon ^{-1})$ and ![]() $O(\varPsi |_b)=O(\epsilon ^{-1})$. Another essential part of the boundary layer is the plume, where the layer is detached from the wall. When the boundary layer leaves the wall, it typically forms a sharp corner. Similar to the RBC cases, as we round the corner, the sizes of
$O(\varPsi |_b)=O(\epsilon ^{-1})$. Another essential part of the boundary layer is the plume, where the layer is detached from the wall. When the boundary layer leaves the wall, it typically forms a sharp corner. Similar to the RBC cases, as we round the corner, the sizes of ![]() $\varOmega$ and
$\varOmega$ and ![]() $\varGamma$ are unchanged. This can be justified by considering a streamline within the boundary layer. The streamline passes through the
$\varGamma$ are unchanged. This can be justified by considering a streamline within the boundary layer. The streamline passes through the ![]() $O(\epsilon ^{1/2})$ neighbourhood of the corner, where the flow is inviscid, hence
$O(\epsilon ^{1/2})$ neighbourhood of the corner, where the flow is inviscid, hence ![]() $\varOmega$ and
$\varOmega$ and ![]() $\varGamma$ are functions of the streamfunction; see also the RBC literature introduced at the beginning of this section.
$\varGamma$ are functions of the streamfunction; see also the RBC literature introduced at the beginning of this section.
The plume layer is no longer parallel to the wall, and the Coriolis force acting there drives the whole Taylor cell. This plume balance allows us to completely fix the flow scaling in terms of ![]() $Ta$. Assuming
$Ta$. Assuming ![]() $\partial _r=O(1)$ and
$\partial _r=O(1)$ and ![]() $\partial _z=O(\epsilon ^{-1})$ in (4.1b), the viscous-convective terms of
$\partial _z=O(\epsilon ^{-1})$ in (4.1b), the viscous-convective terms of ![]() $O(\epsilon ^{-2}\varOmega |_b)=O(\epsilon ^{-5})$ counterbalance the Coriolis term of
$O(\epsilon ^{-2}\varOmega |_b)=O(\epsilon ^{-5})$ counterbalance the Coriolis term of ![]() $O( \epsilon ^{-1}\,Ta)$ when
$O( \epsilon ^{-1}\,Ta)$ when ![]() $\epsilon =Ta^{-1/4}$. Here, we used the fact that within the near-wall boundary layer, the size of
$\epsilon =Ta^{-1/4}$. Here, we used the fact that within the near-wall boundary layer, the size of ![]() $\varGamma$ is
$\varGamma$ is ![]() $O(1)$ from the boundary conditions, and the same size must be used in the plume.
$O(1)$ from the boundary conditions, and the same size must be used in the plume.
The asymptotic structure can be summarised as follows. Within the core region, we use the expansions
where ![]() $\omega _0$ and
$\omega _0$ and ![]() $\gamma _0$ are constants. The expansion is consistent with the Prandtl–Batchelor structure to leading order, and
$\gamma _0$ are constants. The expansion is consistent with the Prandtl–Batchelor structure to leading order, and ![]() $\varPsi _0$ must be determined by
$\varPsi _0$ must be determined by
in the aforementioned region ![]() $\mathcal {A}$ with the boundary condition
$\mathcal {A}$ with the boundary condition ![]() $\varPsi _0=0$ on
$\varPsi _0=0$ on ![]() $\mathcal {C}$.
$\mathcal {C}$.
Let ![]() $l$ and
$l$ and ![]() $n$ be the distance along
$n$ be the distance along ![]() $\mathcal {C}$ and its inward normal, respectively. Then using the rescaled normal variable
$\mathcal {C}$ and its inward normal, respectively. Then using the rescaled normal variable ![]() $N=\epsilon ^{-1} n$, the flow within the boundary layer can be expanded as
$N=\epsilon ^{-1} n$, the flow within the boundary layer can be expanded as
The leading-order equations in the boundary layer are
where ![]() $\varphi$ is the angle between the
$\varphi$ is the angle between the ![]() $z$-axis and the
$z$-axis and the ![]() $n$-axis.
$n$-axis.
When the boundary layer is in contact with the cylinder wall, the following boundary conditions must be imposed at ![]() $N=0$:
$N=0$:
For the near-wall boundary layer, ![]() $\cos \varphi =0$ so (4.12) is none other than Prandtl's boundary layer equation, while for large
$\cos \varphi =0$ so (4.12) is none other than Prandtl's boundary layer equation, while for large ![]() $N$, the flow must match the core solution. Let
$N$, the flow must match the core solution. Let ![]() $U(l)$ be the value of
$U(l)$ be the value of ![]() $\varPsi _{0n}$ on
$\varPsi _{0n}$ on ![]() $\mathcal {C}$, which can be found by the core flow problem (4.9). Then as
$\mathcal {C}$, which can be found by the core flow problem (4.9). Then as ![]() $N\rightarrow \infty$, the boundary layer solution must satisfy
$N\rightarrow \infty$, the boundary layer solution must satisfy
When the boundary layer is detached from the wall, similar far-field conditions should be applied on both sides as ![]() $N\rightarrow \pm \infty$.
$N\rightarrow \pm \infty$.
The theoretical boundary layer thickness ![]() $\epsilon =Ta^{-1/4}$ implies the Nusselt number scaling
$\epsilon =Ta^{-1/4}$ implies the Nusselt number scaling ![]() $Nu\propto Ta^{\beta }$ with
$Nu\propto Ta^{\beta }$ with ![]() $\beta =1/4$. We can check if this is consistent with the angular momentum transport. By averaging (4.1a) with respect to
$\beta =1/4$. We can check if this is consistent with the angular momentum transport. By averaging (4.1a) with respect to ![]() $z$ and further integrating radially from
$z$ and further integrating radially from ![]() $r_i$ to
$r_i$ to ![]() $r$, the transport balance can be obtained as
$r$, the transport balance can be obtained as
Here we use an overline to denote the average with respect to ![]() $z$, and write
$z$, and write ![]() $\varGamma =\bar {\varGamma }(r)+\tilde {\varGamma }(r,z)$. Let us consider this balance at a sufficient distance from both walls. In the core region,
$\varGamma =\bar {\varGamma }(r)+\tilde {\varGamma }(r,z)$. Let us consider this balance at a sufficient distance from both walls. In the core region, ![]() $\tilde {\varGamma }$ would be exponentially small because of the Prandtl–Batchelor theorem, so the transport is extremely inefficient. The plume region of thickness
$\tilde {\varGamma }$ would be exponentially small because of the Prandtl–Batchelor theorem, so the transport is extremely inefficient. The plume region of thickness ![]() $O(\epsilon )$ is hence the main contributor to the left-hand side, which can be estimated as
$O(\epsilon )$ is hence the main contributor to the left-hand side, which can be estimated as ![]() $O(\epsilon (\partial _z \varPsi |_b)\tilde {\varGamma } |_b)=O(\epsilon ^{-1})$ using the scaling
$O(\epsilon (\partial _z \varPsi |_b)\tilde {\varGamma } |_b)=O(\epsilon ^{-1})$ using the scaling ![]() $\tilde {\varGamma }|_b=O(1)$,
$\tilde {\varGamma }|_b=O(1)$, ![]() $\varPsi |_b=O(\epsilon ^{-1})$. This term indeed balances with the second term on the right-hand side.
$\varPsi |_b=O(\epsilon ^{-1})$. This term indeed balances with the second term on the right-hand side.
The asymptotic structure derived here is consistent with the behaviour of the numerical Taylor vortex solution. Figure 6 summarises the numerical results for ![]() $\eta =0.5$,
$\eta =0.5$, ![]() $a=-1/8$. The red solid curve shows the scaling
$a=-1/8$. The red solid curve shows the scaling ![]() $Nu\propto Ta^{1/4}$, which can also be seen in the data presented in figure 1 (
$Nu\propto Ta^{1/4}$, which can also be seen in the data presented in figure 1 (![]() $\eta =5/7$,
$\eta =5/7$, ![]() $a=0$). The green dashed and blue dotted curves are
$a=0$). The green dashed and blue dotted curves are ![]() $Ta^{-1/2}rv$ and
$Ta^{-1/2}rv$ and ![]() $Ta^{-1/2}\omega /r$ measured at the centre of the roll cell. According to the theory, they converge towards the constants
$Ta^{-1/2}\omega /r$ measured at the centre of the roll cell. According to the theory, they converge towards the constants ![]() $\gamma _0$ and
$\gamma _0$ and ![]() $\omega _0$, respectively. The scaling of
$\omega _0$, respectively. The scaling of ![]() $\omega /r$ corresponds to the scaling of
$\omega /r$ corresponds to the scaling of ![]() $u,w$ in the core, and hence the scaling of
$u,w$ in the core, and hence the scaling of ![]() $Re_w$.
$Re_w$.

Figure 6. The large-![]() $Ta$ asymptotic convergence of the Taylor vortex for
$Ta$ asymptotic convergence of the Taylor vortex for ![]() $\eta =0.5$,
$\eta =0.5$, ![]() $k=3$,
$k=3$, ![]() $a=-1/8$. The red solid curve is almost horizontal, implying that the
$a=-1/8$. The red solid curve is almost horizontal, implying that the ![]() $Nu \propto Ta^{1/4}$ scaling derived for
$Nu \propto Ta^{1/4}$ scaling derived for ![]() $k=O(1)$ holds. The green dashed and blue dotted curves are computed by
$k=O(1)$ holds. The green dashed and blue dotted curves are computed by ![]() $v$ and
$v$ and ![]() $\omega$ measured at the centre of the cell
$\omega$ measured at the centre of the cell ![]() $(r,z)=(r_i+0.5,{\rm \pi} /2k)$, respectively.
$(r,z)=(r_i+0.5,{\rm \pi} /2k)$, respectively.
One may have noticed that the exponent ![]() $\beta =1/4$ of the Nusselt number differs from the exponent
$\beta =1/4$ of the Nusselt number differs from the exponent ![]() $\beta =1/3$ deduced in the asymptotic analysis of Chini & Cox (Reference Chini and Cox2009) and Hepworth (Reference Hepworth2014). This discrepancy is due not to the differences in the flow driving mechanism but to the boundary conditions at the walls. If the zero stress condition is imposed, then the linear extrapolation of the core streamfunction already satisfies the boundary condition to leading order. This means that the balance
$\beta =1/3$ deduced in the asymptotic analysis of Chini & Cox (Reference Chini and Cox2009) and Hepworth (Reference Hepworth2014). This discrepancy is due not to the differences in the flow driving mechanism but to the boundary conditions at the walls. If the zero stress condition is imposed, then the linear extrapolation of the core streamfunction already satisfies the boundary condition to leading order. This means that the balance ![]() $O(\varOmega |_b)= O(\epsilon ^{-1}\,Re_w)$ that we assumed for the no-slip case is not necessary. For the slip wall case, the magnitude of the vorticity does not change in the core and the boundary layer, so the strong vortex layer seen in figure 4(c) does not appear. If we use the balance
$O(\varOmega |_b)= O(\epsilon ^{-1}\,Re_w)$ that we assumed for the no-slip case is not necessary. For the slip wall case, the magnitude of the vorticity does not change in the core and the boundary layer, so the strong vortex layer seen in figure 4(c) does not appear. If we use the balance ![]() $O(\varOmega |_b)=O(\varOmega |_c)= O(\epsilon ^{-2})$ instead for the scaling argument of the plume, then we have
$O(\varOmega |_b)=O(\varOmega |_c)= O(\epsilon ^{-2})$ instead for the scaling argument of the plume, then we have ![]() $\epsilon =Ta^{-1/3}$, as expected.
$\epsilon =Ta^{-1/3}$, as expected.
For the slip wall RBC, further analytical progress has been made using the fact that the boundary layer equations become linear and the roll cells are rectangular (Chini & Cox Reference Chini and Cox2009; Hepworth Reference Hepworth2014). In our case, however, we have to rely on numerical calculations because the boundary layer equations are fully nonlinear. Moreover, the shape of the core region is non-trivial due to the small vortices appearing near the corners (see figure 4c). This means that the core and boundary layer equations (4.9), (4.11), (4.12) need to be solved iteratively by updating the core shapes and constants ![]() $\gamma _0$ and
$\gamma _0$ and ![]() $\omega _0$. Such numerical calculations are too challenging and out of the scope of this paper. Differences in the structure of the boundary layer also affect the
$\omega _0$. Such numerical calculations are too challenging and out of the scope of this paper. Differences in the structure of the boundary layer also affect the ![]() $Pr$ dependence of the asymptotic solution of RBC. For the slip wall case, asymptotic solutions for different
$Pr$ dependence of the asymptotic solution of RBC. For the slip wall case, asymptotic solutions for different ![]() $Pr$ can be obtained by rescaling the
$Pr$ can be obtained by rescaling the ![]() $Pr=1$ solution. However, this is possible because the boundary layer is linear, which is not true for the no-slip case.
$Pr=1$ solution. However, this is possible because the boundary layer is linear, which is not true for the no-slip case.
Finally, we show that the above analysis provides some insights into the structure of the mean flow. As already seen in figure 4(b), the angular momentum ![]() $rv$ is almost constant in the core region. Therefore, the mean angular momentum
$rv$ is almost constant in the core region. Therefore, the mean angular momentum ![]() $r\bar {v}$ is expected to become a constant away from the wall. This is indeed the case for the numerical Taylor vortex solution (figure 7a). In the studies of TCF turbulence, on the other hand, the mean angular velocity
$r\bar {v}$ is expected to become a constant away from the wall. This is indeed the case for the numerical Taylor vortex solution (figure 7a). In the studies of TCF turbulence, on the other hand, the mean angular velocity ![]() $q$ is usually plotted, and it is often noted that the profile is linear in the core. At first glance, this appears to be the case, for example, when looking at figure 2(a), but this is because the cylinder gap (
$q$ is usually plotted, and it is often noted that the profile is linear in the core. At first glance, this appears to be the case, for example, when looking at figure 2(a), but this is because the cylinder gap (![]() $\eta \approx 0.714$) is too narrow to clearly see the radial dependence of the profile (see figure 7(a) for the
$\eta \approx 0.714$) is too narrow to clearly see the radial dependence of the profile (see figure 7(a) for the ![]() $q$ profile for a wide gap case
$q$ profile for a wide gap case ![]() $\eta =0.5$). If the numerical results by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b) are summarised in terms of
$\eta =0.5$). If the numerical results by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b) are summarised in terms of ![]() $rv$, as shown in figure 7(b), then they clearly show the constant angular momentum property in the core. Note that when
$rv$, as shown in figure 7(b), then they clearly show the constant angular momentum property in the core. Note that when ![]() $a$ becomes too large, the Taylor vortex appears to favour the vicinity of the inner cylinder, and the homogenisation is observed only there. In the long history of TCF studies, some researchers have also pointed out that the turbulent mean flows might have a uniform angular momentum zone (Wattendorf Reference Wattendorf1935; Taylor Reference Taylor1935; Smith & Townsend Reference Smith and Townsend1982; Lewis & Swinney Reference Lewis and Swinney1999; Dong Reference Dong2007; Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2017). However, this fact is not widely known, probably because the mathematical reasons behind it have not been elucidated.
$a$ becomes too large, the Taylor vortex appears to favour the vicinity of the inner cylinder, and the homogenisation is observed only there. In the long history of TCF studies, some researchers have also pointed out that the turbulent mean flows might have a uniform angular momentum zone (Wattendorf Reference Wattendorf1935; Taylor Reference Taylor1935; Smith & Townsend Reference Smith and Townsend1982; Lewis & Swinney Reference Lewis and Swinney1999; Dong Reference Dong2007; Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2017). However, this fact is not widely known, probably because the mathematical reasons behind it have not been elucidated.

Figure 7. Uniform mean angular momentum profiles. (a) Mean flow of the Taylor vortex solution shown in figure 4 (![]() $\eta =0.5$,
$\eta =0.5$, ![]() $a=-1/8$). The red solid curve is the normalised angular momentum, while the blue dotted curve is the mean angular velocity
$a=-1/8$). The red solid curve is the normalised angular momentum, while the blue dotted curve is the mean angular velocity ![]() $q$ defined in (3.1). (b) Time average of DNS results for
$q$ defined in (3.1). (b) Time average of DNS results for ![]() $Ta=10^{10}$,
$Ta=10^{10}$, ![]() ${a=-0.20},0.00,0.21,0.40,0.60,1.00$. The data are from figure 4 of Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b).
${a=-0.20},0.00,0.21,0.40,0.60,1.00$. The data are from figure 4 of Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b).
5. High-wavenumber Taylor vortices
The aim of this section is to examine the asymptotic behaviour of the solutions at the first and second peaks seen in figure 3(a). To this end, in figure 8, we performed similar calculations at two higher Taylor numbers. The results are summarised using the theoretical scaling to be derived in this section. Essentially, the scalings of ![]() $k$ and
$k$ and ![]() $Nu$ represent the width of the roll cell in the
$Nu$ represent the width of the roll cell in the ![]() $z$ direction and the thickness of the boundary layer adjacent to the cylinder wall, respectively. The computations of the solutions are not easy, especially around the first peak, where very thin boundary layers need to be resolved. Although the convergence of the numerical solutions to the asymptotic states is still not perfect, the theoretical scalings are consistent with the overall features of the numerical data.
$z$ direction and the thickness of the boundary layer adjacent to the cylinder wall, respectively. The computations of the solutions are not easy, especially around the first peak, where very thin boundary layers need to be resolved. Although the convergence of the numerical solutions to the asymptotic states is still not perfect, the theoretical scalings are consistent with the overall features of the numerical data.

Figure 8. Change in the Nusselt number of the Taylor vortex solution when the wavenumber is varied, with (a,b) using the same numerical results. The outer cylinder is stationary (![]() $a=0$), and the radius ratio is
$a=0$), and the radius ratio is ![]() ${\eta =5/7}$. Red solid, green dashed and blue dotted curves correspond to
${\eta =5/7}$. Red solid, green dashed and blue dotted curves correspond to ![]() $Ta=2.95\times 10^{11}$,
$Ta=2.95\times 10^{11}$, ![]() $Ta=7.37\times 10^{10}$ and
$Ta=7.37\times 10^{10}$ and ![]() $Ta=9.75\times 10^9$, respectively. The blue dotted curve is the same as that shown in figure 3. The three crosses in figure 1 are taken from the maxima seen in (a).
$Ta=9.75\times 10^9$, respectively. The blue dotted curve is the same as that shown in figure 3. The three crosses in figure 1 are taken from the maxima seen in (a).
The structure of the flow field in both peaks can be divided roughly into a boundary layer near the wall and a core region in the middle of the gap, as we have seen in figures 2 and 3. On closer inspection, one further notices that the asymptotic structures of the two flows are quite different. For example, in the first peak solution, ![]() $\bar {\varGamma }$ has a flat profile in the core region (figure 9a), but this is not the case in the second peak solution (figure 9b). Figure 10 examines how the core flows develop from the near-wall region adjacent to the inner cylinder. In the first peak solution, the near-wall structure is somewhat similar to the
$\bar {\varGamma }$ has a flat profile in the core region (figure 9a), but this is not the case in the second peak solution (figure 9b). Figure 10 examines how the core flows develop from the near-wall region adjacent to the inner cylinder. In the first peak solution, the near-wall structure is somewhat similar to the ![]() $k=O(1)$ case, with the wall boundary layer becoming a sharp plume as rounding the corner (figure 10a). On the other hand, in the second peak solution, no apparent plume can be recognised away from the wall, and the flow varies only slowly in the
$k=O(1)$ case, with the wall boundary layer becoming a sharp plume as rounding the corner (figure 10a). On the other hand, in the second peak solution, no apparent plume can be recognised away from the wall, and the flow varies only slowly in the ![]() $z$ direction (figure 10b). The core flow inherits this property, as seen from figure 11, where the axial structure of the fluctuation fields is plotted at the mid-gap
$z$ direction (figure 10b). The core flow inherits this property, as seen from figure 11, where the axial structure of the fluctuation fields is plotted at the mid-gap ![]() $r=r_m=(r_o+r_i)/2$. For the second peak solution, only a single Fourier mode plays a major role in the core, while for the first peak, a number of harmonics participate in forming the plume. A theoretical explanation of those differences will be deduced below, together with the detailed scalings of the flows.
$r=r_m=(r_o+r_i)/2$. For the second peak solution, only a single Fourier mode plays a major role in the core, while for the first peak, a number of harmonics participate in forming the plume. A theoretical explanation of those differences will be deduced below, together with the detailed scalings of the flows.

Figure 9. Mean flows for the solutions at the extrema of ![]() $Nu$ seen in figure 8 (
$Nu$ seen in figure 8 (![]() $\eta =5/7$,
$\eta =5/7$, ![]() $a=0$). The red curves are the numerical results at
$a=0$). The red curves are the numerical results at ![]() $Ta=2.95\times 10^{11}$. (a) The first peak. The black solid line is the asymptotic result
$Ta=2.95\times 10^{11}$. (a) The first peak. The black solid line is the asymptotic result ![]() $\bar {\varGamma }=\gamma _0$. The value of
$\bar {\varGamma }=\gamma _0$. The value of ![]() $\gamma _0=0.771$ is estimated at the mid-gap. (b) The second peak. The black curve is the asymptotic result (6.5). The value
$\gamma _0=0.771$ is estimated at the mid-gap. (b) The second peak. The black curve is the asymptotic result (6.5). The value ![]() $A=335.5$ is estimated at the mid-gap (see (6.39)).
$A=335.5$ is estimated at the mid-gap (see (6.39)).

Figure 10. The colour map of ![]() $\omega /r$ for the (a) first peak and (b) second peak solutions seen in figure 8. Here,
$\omega /r$ for the (a) first peak and (b) second peak solutions seen in figure 8. Here, ![]() $Ta=2.95\times 10^{11}$. The centre of the colour bar is zero.
$Ta=2.95\times 10^{11}$. The centre of the colour bar is zero.

Figure 11. The flow fields at the mid-gap ![]() $r=r_m$ for the (a,c) first peak and (b,d) second peak solutions in figure 8. The red solid, green dashed and blue dotted curves correspond to
$r=r_m$ for the (a,c) first peak and (b,d) second peak solutions in figure 8. The red solid, green dashed and blue dotted curves correspond to ![]() $Ta=2.95\times 10^{11}$,
$Ta=2.95\times 10^{11}$, ![]() $Ta=7.37\times 10^{10}$ and
$Ta=7.37\times 10^{10}$ and ![]() $Ta=9.75\times 10^9$, respectively. Note that the value of
$Ta=9.75\times 10^9$, respectively. Note that the value of ![]() $k$ is determined by the optimisation of
$k$ is determined by the optimisation of ![]() $Nu$ and therefore varies from solution to solution. The difference in the structure of the first and second peak solutions can be seen more clearly in figure 10, where the axial coordinates are not scaled.
$Nu$ and therefore varies from solution to solution. The difference in the structure of the first and second peak solutions can be seen more clearly in figure 10, where the axial coordinates are not scaled.
5.1. The first peak asymptotic structure
Now let us find the scaling of the first peak solution. Hereafter, ![]() $\delta =1/k$ denotes the length scale of the cell in the
$\delta =1/k$ denotes the length scale of the cell in the ![]() $z$ direction. The flow can be divided into core and near-wall zones, as shown in figure 5(c). Within the regions
$z$ direction. The flow can be divided into core and near-wall zones, as shown in figure 5(c). Within the regions ![]() $O(\delta )$ away from the cylinder walls, similar asymptotic arguments as the
$O(\delta )$ away from the cylinder walls, similar asymptotic arguments as the ![]() $k=O(1)$ case would apply. Figure 5(b) shows an enlarged view of the near-wall zone where a thin boundary layer, of thickness
$k=O(1)$ case would apply. Figure 5(b) shows an enlarged view of the near-wall zone where a thin boundary layer, of thickness ![]() $\epsilon \ll \delta$ say, emerges around the inviscid region.
$\epsilon \ll \delta$ say, emerges around the inviscid region.
The size of the streamfunction in the inviscid region must be the same as that of the core, ![]() $\varPsi |_c$. Thus the size of the streamfunction within the boundary layer can be found as
$\varPsi |_c$. Thus the size of the streamfunction within the boundary layer can be found as ![]() $O(\varPsi |_b)=O(\epsilon \delta ^{-1} \varPsi |_c)$, noting that the boundary layer thickness relative to the near-wall region is
$O(\varPsi |_b)=O(\epsilon \delta ^{-1} \varPsi |_c)$, noting that the boundary layer thickness relative to the near-wall region is ![]() $\epsilon /\delta$. Further using the viscous-convective balance in the boundary layer
$\epsilon /\delta$. Further using the viscous-convective balance in the boundary layer ![]() $O(\varPsi |_b)=O(\epsilon ^{-1}\delta )$, we can find
$O(\varPsi |_b)=O(\epsilon ^{-1}\delta )$, we can find ![]() $O(\varPsi |_c)=O(\delta ^{2}\epsilon ^{-2})$. When
$O(\varPsi |_c)=O(\delta ^{2}\epsilon ^{-2})$. When ![]() $\bar {\varGamma }|_c$ is almost constant, the viscous-convective balance in the core is satisfied if
$\bar {\varGamma }|_c$ is almost constant, the viscous-convective balance in the core is satisfied if ![]() $O(\varPsi |_c)=O(\delta ^{-1})$. Hence from
$O(\varPsi |_c)=O(\delta ^{-1})$. Hence from ![]() $O(\varPsi |_c)=O(\delta ^{2}\epsilon ^{-2})$ obtained in the near-wall analysis, the two small perturbation parameters are related as
$O(\varPsi |_c)=O(\delta ^{2}\epsilon ^{-2})$ obtained in the near-wall analysis, the two small perturbation parameters are related as ![]() $\epsilon =\delta ^{3/2}$.
$\epsilon =\delta ^{3/2}$.
Within the near-wall zone, the plume coming out of the wall boundary layer is so thin that the Coriolis forces and viscous terms cannot balance, unlike the ![]() $k=O(1)$ case. This means that the Coriolis force effect should appear as the plume diffuses towards the core region.. The viscous-Coriolis balance in the core can be described as
$k=O(1)$ case. This means that the Coriolis force effect should appear as the plume diffuses towards the core region.. The viscous-Coriolis balance in the core can be described as ![]() $O(\varPsi |_c\,\delta ^{-4})=O(Ta\, \delta ^{-1}\tilde {\varGamma }|_c)$. To estimate
$O(\varPsi |_c\,\delta ^{-4})=O(Ta\, \delta ^{-1}\tilde {\varGamma }|_c)$. To estimate ![]() $O(\tilde {\varGamma }|_c)$, we can use the balance
$O(\tilde {\varGamma }|_c)$, we can use the balance ![]() $O(\tilde {\varGamma } |_c\varPsi |_c)=O(\varGamma |_b\varPsi |_b)$, which will be justified shortly. Using the argument of the inviscid corner, we have
$O(\tilde {\varGamma } |_c\varPsi |_c)=O(\varGamma |_b\varPsi |_b)$, which will be justified shortly. Using the argument of the inviscid corner, we have ![]() $O(\varGamma |_b)=O(1)$. Therefore we have the estimation
$O(\varGamma |_b)=O(1)$. Therefore we have the estimation ![]() $O(\tilde {\varGamma }|_c)=O(\epsilon \delta ^{-1})$, which is consistent with the momentum transport balance
$O(\tilde {\varGamma }|_c)=O(\epsilon \delta ^{-1})$, which is consistent with the momentum transport balance ![]() $O((\partial _z \varPsi |_c)\tilde {\varGamma }|_c)=O(Nu)=O(\epsilon ^{-1})$, deduced from (4.16). This is the final key to unlock the scaling
$O((\partial _z \varPsi |_c)\tilde {\varGamma }|_c)=O(Nu)=O(\epsilon ^{-1})$, deduced from (4.16). This is the final key to unlock the scaling ![]() $\delta =O(Ta^{-2/9})$ and
$\delta =O(Ta^{-2/9})$ and ![]() $\epsilon =O(Ta^{-1/3})$, with the latter motivating us to use the
$\epsilon =O(Ta^{-1/3})$, with the latter motivating us to use the ![]() $Nu\propto Ta^{1/3}$ scaling in figure 8(a). The wind Reynolds number can be estimated by the wall-normal velocity component as
$Nu\propto Ta^{1/3}$ scaling in figure 8(a). The wind Reynolds number can be estimated by the wall-normal velocity component as ![]() $Re_w=O(\delta ^{-1}\varPsi |_c)=O(Ta^{4/9})$.
$Re_w=O(\delta ^{-1}\varPsi |_c)=O(Ta^{4/9})$.
The asymptotic analysis in the core is summarised as follows. First, we choose ![]() $\delta$ as a small perturbation parameter and rescale the axial coordinate as
$\delta$ as a small perturbation parameter and rescale the axial coordinate as ![]() $Z=\delta ^{-1} z$. From the scaling argument, the Taylor number has the expansion
$Z=\delta ^{-1} z$. From the scaling argument, the Taylor number has the expansion ![]() $Ta=\delta ^{-9/2}T_0+\cdots$. Using the core expansions
$Ta=\delta ^{-9/2}T_0+\cdots$. Using the core expansions
with a constant ![]() $\gamma _0$ in (4.1) yields the leading-order equations
$\gamma _0$ in (4.1) yields the leading-order equations
Here, only the fluctuation part of the equations was extracted. The mean part can be obtained directly from (4.16) as
using the scaled Nusselt number ![]() $N_0=({16\eta r_i^2}/{(1+\eta )^4})\epsilon \,Nu+\cdots$.
$N_0=({16\eta r_i^2}/{(1+\eta )^4})\epsilon \,Nu+\cdots$.
In the plume near the inner wall, we use the expansions
together with the stretched variables ![]() $l=({r-r_i})/{\delta }$ and
$l=({r-r_i})/{\delta }$ and ![]() $N=z/\epsilon$. The leading-order part of (4.1a) takes the form
$N=z/\epsilon$. The leading-order part of (4.1a) takes the form
which is essentially identical to (4.11). If we consider that ![]() $\varGamma ^{(b)}$ is a function of
$\varGamma ^{(b)}$ is a function of ![]() $\psi =\varPsi ^{(b)}$ and
$\psi =\varPsi ^{(b)}$ and ![]() $l$, then the equation becomes
$l$, then the equation becomes
where ![]() $\varGamma _{\psi }^{(b)}$ should be small when far enough away from the plume. By integrating this equation across the plume, we get
$\varGamma _{\psi }^{(b)}$ should be small when far enough away from the plume. By integrating this equation across the plume, we get
The term in the bracket is conserved during the plume diffusion so that the balance ![]() $O(\tilde {\varGamma } |_c\,\varPsi |_c)=O(\varGamma |_b\,\varPsi |_b)$ must be satisfied. The effect of the plume entering the core has to be described by boundary conditions for (5.2)–(5.3) at
$O(\tilde {\varGamma } |_c\,\varPsi |_c)=O(\varGamma |_b\,\varPsi |_b)$ must be satisfied. The effect of the plume entering the core has to be described by boundary conditions for (5.2)–(5.3) at ![]() $r=r_i,r_o$. The conditions could be written using the Dirac delta function as done in Vynnycky & Masuda (Reference Vynnycky and Masuda2013).
$r=r_i,r_o$. The conditions could be written using the Dirac delta function as done in Vynnycky & Masuda (Reference Vynnycky and Masuda2013).
We do not solve the asymptotic problem, but the theory well explains the behaviour of the Taylor vortex solution. For example, the numerical results shown in figures 11(a) and 11(c) are summarised using the theoretical core scalings ![]() $\varOmega |_c=O(\delta ^{-2}\varPsi |_c)=O(Ta^{2/3})$ and
$\varOmega |_c=O(\delta ^{-2}\varPsi |_c)=O(Ta^{2/3})$ and ![]() $\tilde {\varGamma }|_c=O(Ta^{-1/9})$. In figure 9(a), the thin black line is the asymptotic approximation
$\tilde {\varGamma }|_c=O(Ta^{-1/9})$. In figure 9(a), the thin black line is the asymptotic approximation ![]() $\bar {\varGamma }\approx \gamma _0$ with the estimate
$\bar {\varGamma }\approx \gamma _0$ with the estimate ![]() $\gamma _0=Ta^{-1/2}\,r_m\, \bar {v}(r_m)\approx 0.771$.
$\gamma _0=Ta^{-1/2}\,r_m\, \bar {v}(r_m)\approx 0.771$.
From the numerical data, the Nusselt number at the first peak seems to be approximated by ![]() $Nu=0.027\,Ta^{1/3}$. The asymptotic line intersects with the
$Nu=0.027\,Ta^{1/3}$. The asymptotic line intersects with the ![]() $k=3$ curve shown in figure 1 at
$k=3$ curve shown in figure 1 at ![]() $Ta\approx 6\times 10^7$, which is not a bad approximation of the transition point between the classical and ultimate turbulence regimes.
$Ta\approx 6\times 10^7$, which is not a bad approximation of the transition point between the classical and ultimate turbulence regimes.
5.2. The second peak asymptotic structure
The asymptotic structure of the second peak solution is more complex because three layers appear in the vicinity of the walls (see figure 12a). We refer to them as the bottom, middle and top boundary layers, in order from the cylinder wall. Understanding their precise scaling requires a delicate matched asymptotic expansion analysis, which we will leave for the next section. Here we will look only at how the flow scaling is determined intuitively. The argument below contains one assumption that is not strictly fulfilled, but the resultant scaling is nonetheless correct if some minor logarithmic factor effects are omitted.

Figure 12. Sketch similar to figure 5 but for the asymptotic states when ![]() $k=Ta^{1/4}$. (a) The second peak state. BL stands for boundary layer. (b) The transitional state. The shear layer occurs around the critical radius
$k=Ta^{1/4}$. (a) The second peak state. BL stands for boundary layer. (b) The transitional state. The shear layer occurs around the critical radius ![]() $r=r_c$.
$r=r_c$.
The key assumption is ![]() ${{\rm d}\bar {\varGamma }}/{{\rm d}r}=O(1)$ in the core, which did not hold for the first peak case. If the governing equations (4.1a) and (4.1b) are linearised around the mean flow, then the balances
${{\rm d}\bar {\varGamma }}/{{\rm d}r}=O(1)$ in the core, which did not hold for the first peak case. If the governing equations (4.1a) and (4.1b) are linearised around the mean flow, then the balances ![]() $O(\delta ^{-1}\varPsi |_c)=O(\delta ^{-2}\tilde {\varGamma })$ and
$O(\delta ^{-1}\varPsi |_c)=O(\delta ^{-2}\tilde {\varGamma })$ and ![]() $O(\delta ^{-4}\varPsi |_c)=O(\delta ^{-1}Ta\, \tilde {\varGamma }|_c)$ must be satisfied. Those balances determine
$O(\delta ^{-4}\varPsi |_c)=O(\delta ^{-1}Ta\, \tilde {\varGamma }|_c)$ must be satisfied. Those balances determine ![]() $\delta =O(Ta^{-1/4})$ and
$\delta =O(Ta^{-1/4})$ and ![]() $O(\tilde {\varGamma }|_c)=O(\delta \varPsi |_c)$. Further using
$O(\tilde {\varGamma }|_c)=O(\delta \varPsi |_c)$. Further using ![]() $O((\partial _z \varPsi |_c)\tilde {\varGamma }|_c)=O(Nu)=O(\epsilon ^{-1})$ deduced from the mean equation (4.16), the core flow scaling can be written as
$O((\partial _z \varPsi |_c)\tilde {\varGamma }|_c)=O(Nu)=O(\epsilon ^{-1})$ deduced from the mean equation (4.16), the core flow scaling can be written as ![]() $O(\varPsi |_c)=O(\epsilon ^{-1/2})$,
$O(\varPsi |_c)=O(\epsilon ^{-1/2})$, ![]() $O(\tilde {\varGamma }|_c)=O(\delta \epsilon ^{-1/2})$.
$O(\tilde {\varGamma }|_c)=O(\delta \epsilon ^{-1/2})$.
Within the bottom boundary layer, the viscous-convective balance ![]() $O(\varPsi |_b)=O(\epsilon ^{-1} \delta )$ must, of course, be satisfied (the subscript
$O(\varPsi |_b)=O(\epsilon ^{-1} \delta )$ must, of course, be satisfied (the subscript ![]() $b$ implies that
$b$ implies that ![]() $\varPsi$ is measured at the bottom boundary layer). If we further assume the viscous-Coriolis balance
$\varPsi$ is measured at the bottom boundary layer). If we further assume the viscous-Coriolis balance ![]() $O(\varPsi |_b)=O(Ta\,\epsilon ^{4} \delta ^{-1})$, then we obtain
$O(\varPsi |_b)=O(Ta\,\epsilon ^{4} \delta ^{-1})$, then we obtain ![]() $\epsilon =\delta ^{6/5}=Ta^{-3/10}$, which gives
$\epsilon =\delta ^{6/5}=Ta^{-3/10}$, which gives ![]() $Nu\propto Ta^{3/10}$ in figure 8(b). It is this balance that is mostly met, but in fact, is a little broken. As mentioned earlier, the effect of this slight imbalance appears as a logarithmic factor in the scaling of
$Nu\propto Ta^{3/10}$ in figure 8(b). It is this balance that is mostly met, but in fact, is a little broken. As mentioned earlier, the effect of this slight imbalance appears as a logarithmic factor in the scaling of ![]() $\epsilon$ in the matched asymptotic expansion. The introduction of the logarithmic factor has little influence when examining the scaling of numerical data, so it was ignored in figure 8(b). Furthermore, as shown in figures 11(b) and 11(d), the core scalings
$\epsilon$ in the matched asymptotic expansion. The introduction of the logarithmic factor has little influence when examining the scaling of numerical data, so it was ignored in figure 8(b). Furthermore, as shown in figures 11(b) and 11(d), the core scalings ![]() $O(\varOmega |_c)=O(\delta ^{-2}\varPsi |_c)=O(Ta^{13/20})$ and
$O(\varOmega |_c)=O(\delta ^{-2}\varPsi |_c)=O(Ta^{13/20})$ and ![]() $\tilde {\varGamma }|_c=O(Ta^{-1/10})$ without the logarithmic factor well explain the numerical results. Note that the scaling result suggests
$\tilde {\varGamma }|_c=O(Ta^{-1/10})$ without the logarithmic factor well explain the numerical results. Note that the scaling result suggests ![]() $Re_w=O(\delta ^{-1}\varPsi |_c)=O(\delta ^{-1}\epsilon ^{-1/2})=O(Ta^{2/5})$.
$Re_w=O(\delta ^{-1}\varPsi |_c)=O(\delta ^{-1}\epsilon ^{-1/2})=O(Ta^{2/5})$.
In the middle boundary layer, the flow coming towards the wall turns back in the region of aspect ratio approximately unity, so its thickness should be ![]() $O(\delta )$.
$O(\delta )$.
The top boundary layer is necessary for the nonlinearity of the fluctuation component to disappear towards the core. Its thickness ![]() $\varDelta =O(\delta \epsilon ^{-1/2})=O(Ta^{-1/10})$ can be obtained by the viscous-convective balance
$\varDelta =O(\delta \epsilon ^{-1/2})=O(Ta^{-1/10})$ can be obtained by the viscous-convective balance ![]() $O(\varDelta ^{-1}\delta ^{-1}\varPsi |_t)=O(\delta ^{-2})$ and
$O(\varDelta ^{-1}\delta ^{-1}\varPsi |_t)=O(\delta ^{-2})$ and ![]() $O(\varPsi |_t)=O(\varPsi |_c)$, where
$O(\varPsi |_t)=O(\varPsi |_c)$, where ![]() $O(\varPsi |_t)$ is the size of the streamfunction in the top boundary layer. One of the ways to ascertain the presence of the top boundary layer in the visualised flow field is to look at the extreme values of
$O(\varPsi |_t)$ is the size of the streamfunction in the top boundary layer. One of the ways to ascertain the presence of the top boundary layer in the visualised flow field is to look at the extreme values of ![]() $\varOmega$ (see figure 10(b)) or
$\varOmega$ (see figure 10(b)) or ![]() $\tilde {\varGamma }$. Figure 13(a) shows the scaled fluctuation
$\tilde {\varGamma }$. Figure 13(a) shows the scaled fluctuation ![]() $\tilde {\varGamma }$ at the plume position
$\tilde {\varGamma }$ at the plume position ![]() $z={\rm \pi} /k$. It can be seen that the minima approach the wall as the Taylor number increases. In figure 13(b), the distance between the wall and the minima is scaled by the theoretical top boundary layer thickness
$z={\rm \pi} /k$. It can be seen that the minima approach the wall as the Taylor number increases. In figure 13(b), the distance between the wall and the minima is scaled by the theoretical top boundary layer thickness ![]() $\varDelta$. As expected, all the curves almost overlap around the minima.
$\varDelta$. As expected, all the curves almost overlap around the minima.

Figure 13. The profile of ![]() $\tilde {\varGamma }$ at the plume position
$\tilde {\varGamma }$ at the plume position ![]() $z={\rm \pi} /k$ for the Taylor vortex solution at the second peak, with
$z={\rm \pi} /k$ for the Taylor vortex solution at the second peak, with ![]() $\eta =5/7$,
$\eta =5/7$, ![]() $a=0$. The red solid, green dashed and blue dotted curves correspond to
$a=0$. The red solid, green dashed and blue dotted curves correspond to ![]() $Ta=2.95\times 10^{11}$,
$Ta=2.95\times 10^{11}$, ![]() $Ta=7.37\times 10^{10}$ and
$Ta=7.37\times 10^{10}$ and ![]() $Ta=9.75\times 10^9$, respectively.
$Ta=9.75\times 10^9$, respectively.
6. Matched asymptotic expansion when  $k=O(Ta^{1/4})$
$k=O(Ta^{1/4})$
The goal of this section is to derive a matched asymptotic expansion consistent with the behaviour of the second peak solutions. This asymptotic state can be reached by decreasing the wavenumber from the linear critical point, as seen in figure 8(b). However, for ![]() $k/Ta^{1/4}$ ranging from approximately 0.6 to 0.8, the appropriate scaling of the Nusselt number is
$k/Ta^{1/4}$ ranging from approximately 0.6 to 0.8, the appropriate scaling of the Nusselt number is ![]() $O(Ta^0)$, which is different from that observed for the second peak state; see figure 14(a). We will study this transitional state in § 6.1, followed by the analysis of the second peak in § 6.2.
$O(Ta^0)$, which is different from that observed for the second peak state; see figure 14(a). We will study this transitional state in § 6.1, followed by the analysis of the second peak in § 6.2.

Figure 14. (a) Close-up of figure 8(b) around the bifurcation point. The black solid curve is the asymptotic result (6.17), which has the property that ![]() $Nu=1$ at
$Nu=1$ at ![]() $k/Ta^{1/4}=K_1$, and that
$k/Ta^{1/4}=K_1$, and that ![]() $Nu\rightarrow \infty$ as
$Nu\rightarrow \infty$ as ![]() $k/Ta^{1/4}\rightarrow K_{\infty }$. (b) Mean flow profile at
$k/Ta^{1/4}\rightarrow K_{\infty }$. (b) Mean flow profile at ![]() $k/Ta^{1/4}=0.65, 0.7$. The black solid curves are the asymptotic result (6.15). The bullets indicate
$k/Ta^{1/4}=0.65, 0.7$. The black solid curves are the asymptotic result (6.15). The bullets indicate ![]() $r=r_c$ given in (6.13). The red points are the numerical Taylor vortex result for
$r=r_c$ given in (6.13). The red points are the numerical Taylor vortex result for ![]() $Ta=9.75\times 10^9$. (c) Colour maps of
$Ta=9.75\times 10^9$. (c) Colour maps of ![]() $\omega /r$ for the numerical Taylor vortex. The top and bottom maps correspond to
$\omega /r$ for the numerical Taylor vortex. The top and bottom maps correspond to ![]() $k/Ta^{1/4}=0.7$ and 0.65, respectively. Lines are marked at
$k/Ta^{1/4}=0.7$ and 0.65, respectively. Lines are marked at ![]() $r=r_c$.
$r=r_c$.
The most important previous work throughout this section is due to Denier (Reference Denier1992), who applied the Hall & Lakin (Reference Hall and Lakin1988) type high-wavenumber asymptotic theory to TCF in the narrow gap limit. As briefly commented in that paper, the extension of the theory to wide-gap cases should be straightforward. In § 6.1, we derive an analytic expression for the Nusselt number and compare it with the numerical solution for the first time.
As the solution moves away from the linear critical point in the transitional state, the vortex grows from the vicinity of the inner cylinder (figure 14c). The asymptotic state corresponding to the second peak appears when the vortex fills the entire gap. A similar scenario was suggested in Denier (Reference Denier1992) using a matched asymptotic expansion, but the scaling obtained is unfortunately not consistent with the behaviour of the numerical solutions. The main reason for this is that the matching is not actually possible in the two-layer boundary layer structure assumed in Denier (Reference Denier1992). In § 6.2, we will resolve that difficulty by modifying the structure of the near-wall zone to three layers.
We choose ![]() $\delta =k^{-1}$ as a small perturbation parameter and introduce the scaled axial variable
$\delta =k^{-1}$ as a small perturbation parameter and introduce the scaled axial variable ![]() $Z=\delta ^{-1}z$. According to Hall (Reference Hall1982), the linear critical point of curved flow problems typically has the Taylor number expansion
$Z=\delta ^{-1}z$. According to Hall (Reference Hall1982), the linear critical point of curved flow problems typically has the Taylor number expansion ![]() $Ta=\delta ^{-4} T_0+\cdots$. This is also true for TCF from the linear critical point to the second peak.
$Ta=\delta ^{-4} T_0+\cdots$. This is also true for TCF from the linear critical point to the second peak.
6.1. The transitional states around the linear critical point
For simplicity, we fix the outer cylinder (i.e. ![]() $a=\varGamma _o=0$) as in Denier (Reference Denier1992). The analysis of the general cases (
$a=\varGamma _o=0$) as in Denier (Reference Denier1992). The analysis of the general cases (![]() $a\neq 0$) is relegated to Appendix B as it is somewhat complex. The asymptotic structure of the transitional state is depicted in figure 12(b). The vortices are concentrated in the core region
$a\neq 0$) is relegated to Appendix B as it is somewhat complex. The asymptotic structure of the transitional state is depicted in figure 12(b). The vortices are concentrated in the core region ![]() $r_i< r< r_c$, where
$r_i< r< r_c$, where ![]() $r_c \in [r_i,r_o]$ is the critical radius to be determined analytically. We can show that the vortex amplitude decays exponentially within a shear layer of thickness
$r_c \in [r_i,r_o]$ is the critical radius to be determined analytically. We can show that the vortex amplitude decays exponentially within a shear layer of thickness ![]() $O(\varDelta )=O(Ta^{-1/6})$ appearing around the critical radius. The structure of the shear layer is identical to that described in Denier (Reference Denier1992) and is not discussed in detail here. The only important fact that will be used later is that the mean flow and its derivative are continuous across this layer.
$O(\varDelta )=O(Ta^{-1/6})$ appearing around the critical radius. The structure of the shear layer is identical to that described in Denier (Reference Denier1992) and is not discussed in detail here. The only important fact that will be used later is that the mean flow and its derivative are continuous across this layer.
In the region where ![]() $r$ is greater than
$r$ is greater than ![]() $r_c$, it is sufficient to analyse the mean flow. To leading order, the left-hand side of (4.16) can be ignored, hence the mean flow is a linear combination of a constant and
$r_c$, it is sufficient to analyse the mean flow. To leading order, the left-hand side of (4.16) can be ignored, hence the mean flow is a linear combination of a constant and ![]() $r^2$. Writing
$r^2$. Writing
for simplicity, we get the asymptotic approximation
Note that we used the fact that ![]() $\bar {\varGamma }$ should vanish at
$\bar {\varGamma }$ should vanish at ![]() $r=r_o$.
$r=r_o$.
In the core region, the appropriate expansions are
Substituting these into (4.1), the leading-order parts yield
For those equations to have a non-trivial solution, ![]() $0=r^3+2T_0\bar {\varGamma }^{(c)}\bar {\varGamma }^{(c)}_r$ must be satisfied. Therefore the mean flow is obtained as
$0=r^3+2T_0\bar {\varGamma }^{(c)}\bar {\varGamma }^{(c)}_r$ must be satisfied. Therefore the mean flow is obtained as
 \begin{equation} \bar{\varGamma}^{(c)}(r)=\sqrt{\frac{A-r^4}{4T_0}}.\end{equation}
\begin{equation} \bar{\varGamma}^{(c)}(r)=\sqrt{\frac{A-r^4}{4T_0}}.\end{equation}
The constant ![]() $A$ must be
$A$ must be
to satisfy ![]() $\bar {\varGamma }^{(c)}(r_i)=\varGamma _i$.
$\bar {\varGamma }^{(c)}(r_i)=\varGamma _i$.
A boundary layer of thickness ![]() $O(\delta )$ is needed near the inner cylinder to satisfy the no-slip boundary conditions. In this layer, we introduce the stretched variable
$O(\delta )$ is needed near the inner cylinder to satisfy the no-slip boundary conditions. In this layer, we introduce the stretched variable ![]() $\xi =({r-r_i})/{\delta }$ and assume the expansion
$\xi =({r-r_i})/{\delta }$ and assume the expansion
The leading-order equations are obtained as
The no-slip boundary conditions are
while for the far field, ![]() $\xi \rightarrow \infty$, we use the matching conditions
$\xi \rightarrow \infty$, we use the matching conditions
Finally, we determine the unknown constants ![]() $B$ and
$B$ and ![]() $r_c$ from the continuity of
$r_c$ from the continuity of ![]() $\bar {\varGamma }$ and
$\bar {\varGamma }$ and ![]() $r^3(r^{-2}\bar {\varGamma })_r$ at
$r^3(r^{-2}\bar {\varGamma })_r$ at ![]() $r=r_c$. Using the mean flows (6.5) and (6.2a), the continuity conditions can be written as
$r=r_c$. Using the mean flows (6.5) and (6.2a), the continuity conditions can be written as
 \begin{equation} \sqrt{\frac{A-r_c^4}{4T_0}}=B(r_o^2-r_c^2),\quad \frac{A}{\sqrt{T_0(A-r_c^4)}}=2Br_o^2, \end{equation}
\begin{equation} \sqrt{\frac{A-r_c^4}{4T_0}}=B(r_o^2-r_c^2),\quad \frac{A}{\sqrt{T_0(A-r_c^4)}}=2Br_o^2, \end{equation}
where ![]() $A$ is known by (6.6). From those equations, it is easy to find
$A$ is known by (6.6). From those equations, it is easy to find
 $$\begin{gather} r_c=\sqrt{\frac{r_i^4+4T_0\varGamma_i^2}{r_o^2}}, \end{gather}$$
$$\begin{gather} r_c=\sqrt{\frac{r_i^4+4T_0\varGamma_i^2}{r_o^2}}, \end{gather}$$ $$\begin{gather}\frac{1}{B}=\sqrt{4T_0\left (\frac{r_o^4}{r_i^4+4T_0\varGamma_i^2}-1 \right )}. \end{gather}$$
$$\begin{gather}\frac{1}{B}=\sqrt{4T_0\left (\frac{r_o^4}{r_i^4+4T_0\varGamma_i^2}-1 \right )}. \end{gather}$$
Thus if ![]() $T_0$ is given, then the leading-order mean flow is completely determined as
$T_0$ is given, then the leading-order mean flow is completely determined as
 \begin{equation}
\bar{\varGamma}\approx \left \{\begin{array}{@{}ll@{}}
(r_o^2-r^2)\sqrt{\dfrac{r_i^4+4T_0\varGamma_i^2}{4T_0\left
(r_o^4-r_i^4-4T_0\varGamma_i^2 \right )}} & \text{if} \ r>
r_c,\\[14pt]
\sqrt{\dfrac{r_i^4-r^4+4T_0\varGamma_i^2}{4T_0}} &
\text{if} \ r\leq r_c. \end{array} \right .
\end{equation}
\begin{equation}
\bar{\varGamma}\approx \left \{\begin{array}{@{}ll@{}}
(r_o^2-r^2)\sqrt{\dfrac{r_i^4+4T_0\varGamma_i^2}{4T_0\left
(r_o^4-r_i^4-4T_0\varGamma_i^2 \right )}} & \text{if} \ r>
r_c,\\[14pt]
\sqrt{\dfrac{r_i^4-r^4+4T_0\varGamma_i^2}{4T_0}} &
\text{if} \ r\leq r_c. \end{array} \right .
\end{equation}
This is the black curve in figure 14(b), which predicts the numerical results very well. Note that the analytic expression for ![]() $\hat {\varPsi }^{(c)}$ and
$\hat {\varPsi }^{(c)}$ and ![]() $\hat {\varGamma }^{(c)}$ can also be found by (6.4a,b) and the leading-order part of the mean flow equation (4.16):
$\hat {\varGamma }^{(c)}$ can also be found by (6.4a,b) and the leading-order part of the mean flow equation (4.16):
The Nusselt number is found using (6.1), (6.2b) and (6.14) as
 \begin{equation} Nu(T_0)=\frac{(1+\eta)^4}{16\eta^3\sqrt{T_0}}\sqrt{\frac{r_i^4+4T_0\varGamma_i^2}{r_o^4-r_i^4-4T_0\varGamma_i^2}}.\end{equation}
\begin{equation} Nu(T_0)=\frac{(1+\eta)^4}{16\eta^3\sqrt{T_0}}\sqrt{\frac{r_i^4+4T_0\varGamma_i^2}{r_o^4-r_i^4-4T_0\varGamma_i^2}}.\end{equation}
This function is plotted by the black curve in figure 14(a), using ![]() $k/Ta^{1/4}= T_0^{-1/4}$ for the horizontal axis. The other curves, corresponding to the Taylor vortex solutions at finite
$k/Ta^{1/4}= T_0^{-1/4}$ for the horizontal axis. The other curves, corresponding to the Taylor vortex solutions at finite ![]() $Ta$, clearly approach the asymptotic result as
$Ta$, clearly approach the asymptotic result as ![]() $Ta\rightarrow \infty$.
$Ta\rightarrow \infty$.
As the scaled wavenumber decreases from the linear critical point ![]() $K_1=T_1^{-1/4}$, the Nusselt number increases from the laminar value unity. The asymptotic result
$K_1=T_1^{-1/4}$, the Nusselt number increases from the laminar value unity. The asymptotic result ![]() $T_1={r_i^2(r_o^2-r_i^2)}/{4\varGamma _i^2}$ can be found from (6.13) by setting
$T_1={r_i^2(r_o^2-r_i^2)}/{4\varGamma _i^2}$ can be found from (6.13) by setting ![]() $r_c=r_i$ and
$r_c=r_i$ and ![]() $T_0=T_1$.
$T_0=T_1$.
Similar to the narrow gap case studied by Denier (Reference Denier1992), ![]() $Nu$ blows up at finite
$Nu$ blows up at finite ![]() $T_0$. Writing
$T_0$. Writing ![]() $K_{\infty }=T_{\infty }^{-1/4}$, we can deduce
$K_{\infty }=T_{\infty }^{-1/4}$, we can deduce ![]() $T_{\infty }=({r_o^4-r_i^4})/{4\varGamma _i^2}$ from (6.13) by using
$T_{\infty }=({r_o^4-r_i^4})/{4\varGamma _i^2}$ from (6.13) by using ![]() $r_c=r_o$ and
$r_c=r_o$ and ![]() $T_0=T_{\infty }$. That is, in figure 14(a),
$T_0=T_{\infty }$. That is, in figure 14(a), ![]() $K_{\infty }$ is the point at which the flow switches from the transitional state to the second peak state.
$K_{\infty }$ is the point at which the flow switches from the transitional state to the second peak state.
6.2. The second peak states
We now turn our attention to the second peak asymptotic states. Again, ![]() $\delta$ is the small asymptotic parameter, and
$\delta$ is the small asymptotic parameter, and ![]() $Ta=\delta ^{-4}T_0+\cdots$. For the bottom boundary layer thickness
$Ta=\delta ^{-4}T_0+\cdots$. For the bottom boundary layer thickness ![]() $\epsilon$, we impose the condition
$\epsilon$, we impose the condition
which is needed for successful matching. The boundary layer thickness is estimated as ![]() $O(\epsilon )=O(Ta^{-3/10}(\ln Ta)^{-1/5})$. Therefore the Nusselt number and the wind Reynolds number scalings now involve the logarithmic correction as
$O(\epsilon )=O(Ta^{-3/10}(\ln Ta)^{-1/5})$. Therefore the Nusselt number and the wind Reynolds number scalings now involve the logarithmic correction as ![]() $Nu=O(\epsilon ^{-1})=O(Ta^{3/10}(\ln Ta)^{1/5})$,
$Nu=O(\epsilon ^{-1})=O(Ta^{3/10}(\ln Ta)^{1/5})$, ![]() $Re_w=O(\delta ^{-1}\varPsi |_c)=O(\delta ^{-1}\epsilon ^{-1/2})=O(Ta^{2/5}(\ln Ta)^{1/10})$.
$Re_w=O(\delta ^{-1}\varPsi |_c)=O(\delta ^{-1}\epsilon ^{-1/2})=O(Ta^{2/5}(\ln Ta)^{1/10})$.
Let us start with the core analysis by writing
Those expansions, based on the argument in § 5, yield leading-order equations (6.4a,b) identical to those for the transitional state. As a result, the mean flow is given by (6.5). However, for the second peak state, the multi-layered near-wall structure must also be present near the outer cylinder, thus there is no way to determine the constant ![]() $A$ a priori. The leading-order part of the mean flow equation (4.16) is obtained as
$A$ a priori. The leading-order part of the mean flow equation (4.16) is obtained as
where ![]() $N_0=({16\eta r_i^2}/{(1+\eta )^4})\epsilon \,Nu$. The unknowns appearing in the core solutions
$N_0=({16\eta r_i^2}/{(1+\eta )^4})\epsilon \,Nu$. The unknowns appearing in the core solutions ![]() $\bar {\varGamma }^{(c)}, \hat {\varPsi }^{(c)}$ and
$\bar {\varGamma }^{(c)}, \hat {\varPsi }^{(c)}$ and ![]() $\hat {\varGamma }^{(c)}$ are
$\hat {\varGamma }^{(c)}$ are ![]() $A$ and
$A$ and ![]() $N_0$.
$N_0$.
The two near-wall regions have identical asymptotic structure, so only the layers near the inner cylinder are examined below. The top boundary layer expansions are
where the constant ![]() $\gamma _i=\bar {\varGamma }^{(c)}(r_i)$ comes from the leading-order core mean flow. The stretched variable
$\gamma _i=\bar {\varGamma }^{(c)}(r_i)$ comes from the leading-order core mean flow. The stretched variable ![]() $\zeta =({r-r_i})/{\varDelta }$ is defined by using the top boundary layer thickness
$\zeta =({r-r_i})/{\varDelta }$ is defined by using the top boundary layer thickness ![]() $\varDelta =\delta \epsilon ^{-1/2}=O(Ta^{-1/10}(\ln Ta)^{1/10})$. The leading-order governing equations for the top boundary layer are similar to those for the core region in the first peak states:
$\varDelta =\delta \epsilon ^{-1/2}=O(Ta^{-1/10}(\ln Ta)^{1/10})$. The leading-order governing equations for the top boundary layer are similar to those for the core region in the first peak states:
As ![]() $\zeta \rightarrow \infty$, the flow matches to the core solution as
$\zeta \rightarrow \infty$, the flow matches to the core solution as
while the asymptotic behaviour of the flow towards the wall should be
which is similar to that used in Denier (Reference Denier1992). However, to match this with the bottom boundary layer, we must insert the middle boundary layer.
Recall that the middle boundary layer is the special place where the radial and axial derivatives of the flow have the same size. Thus the expansions there must be written in terms of ![]() $\xi =({r-r_i})/{\delta }$ as
$\xi =({r-r_i})/{\delta }$ as
Given the expansions, it is a straightforward task to find that the leading-order equations
are inviscid. Here, the Coriolis force term participating in (6.30) is critical for successful matching to the top boundary layer:
On the other hand, the appropriate behaviour of the solution towards the wall, ![]() $\xi \rightarrow 0$, can be found as
$\xi \rightarrow 0$, can be found as
by seeking the consistent limiting behaviour of the solution. The key observation here is that for both matching conditions, the rate of increase in ![]() $\varPsi$ and the rate of decrease in
$\varPsi$ and the rate of decrease in ![]() $\varGamma$ are the same when moving away from the wall. This is a requirement to satisfy the angular momentum transport balance (6.31).
$\varGamma$ are the same when moving away from the wall. This is a requirement to satisfy the angular momentum transport balance (6.31).
The leading-order part of the bottom boundary layer expansions
matches the middle boundary layer if (6.18) holds and
as ![]() $Y=({r-r_i})/{\epsilon } \rightarrow \infty$. The leading-order equations in the bottom boundary layer are
$Y=({r-r_i})/{\epsilon } \rightarrow \infty$. The leading-order equations in the bottom boundary layer are
Thanks to the radial diffusivity, the no-slip boundary conditions
can be imposed.
Although the combined boundary layers appear rather complex, their role is merely to define the relationship between ![]() $A$ and
$A$ and ![]() $N_0$. Once
$N_0$. Once ![]() $T_0$ and
$T_0$ and ![]() $A$ are fixed, the flow near the inner cylinder can be calculated to find
$A$ are fixed, the flow near the inner cylinder can be calculated to find ![]() $N_0=f_i(A,T_0)$. A similar calculation for the near outer cylinder region yields another functional relationship
$N_0=f_i(A,T_0)$. A similar calculation for the near outer cylinder region yields another functional relationship ![]() $N_0=f_o(A,T_0)$. Hence, in principle,
$N_0=f_o(A,T_0)$. Hence, in principle, ![]() $A(T_0)$ and
$A(T_0)$ and ![]() $N_0(T_0)$ can be determined by solving the two near-wall regions numerically. We do not perform such challenging calculations since we have already seen in § 5 that the finite
$N_0(T_0)$ can be determined by solving the two near-wall regions numerically. We do not perform such challenging calculations since we have already seen in § 5 that the finite ![]() $Ta$ numerical results are consistent with the asymptotic theory.
$Ta$ numerical results are consistent with the asymptotic theory.
The value of ![]() $A$ can be predicted from the finite
$A$ can be predicted from the finite ![]() $Ta$ numerical solutions as
$Ta$ numerical solutions as
by using the mean flow at the mid-gap. The black curve in figure 9(b) is the result of using this ![]() $A$ in (6.5), and it can be seen that this asymptotic prediction matches the numerical calculation in the entire core region. Similarly, the fluctuation component in the core can be calculated explicitly. The black curve in figure 15 is the asymptotic approximation
$A$ in (6.5), and it can be seen that this asymptotic prediction matches the numerical calculation in the entire core region. Similarly, the fluctuation component in the core can be calculated explicitly. The black curve in figure 15 is the asymptotic approximation
 \begin{equation} \tilde{\varGamma}\approx Ta^{{-}1/4}\,r\left (\frac{32\eta r_i^2}{(1+\eta)^4}\,\frac{Nu}{\sqrt{(A-r^4)}} \right )^{1/2} \cos Z,\end{equation}
\begin{equation} \tilde{\varGamma}\approx Ta^{{-}1/4}\,r\left (\frac{32\eta r_i^2}{(1+\eta)^4}\,\frac{Nu}{\sqrt{(A-r^4)}} \right )^{1/2} \cos Z,\end{equation}which is in good agreement with the numerical result.
We will also comment briefly on the case where ![]() $a$ is non-zero. For any
$a$ is non-zero. For any ![]() $a$, it is not so difficult to decrease
$a$, it is not so difficult to decrease ![]() $k$ of the Taylor vortex solution branch from the linear critical point until the Nusselt number takes a peak. The red crosses in figure 16(a) summarise
$k$ of the Taylor vortex solution branch from the linear critical point until the Nusselt number takes a peak. The red crosses in figure 16(a) summarise ![]() $Nu$ at the peak for various
$Nu$ at the peak for various ![]() $a$. The numerical result shows that the optimised
$a$. The numerical result shows that the optimised ![]() $Nu$ is maximised when the outer cylinder slightly counter-rotates (
$Nu$ is maximised when the outer cylinder slightly counter-rotates (![]() $a\approx 0.08$). This is in line qualitatively with the experimental ultimate turbulence results shown by green squares. However, for the experimental results, the maximum of
$a\approx 0.08$). This is in line qualitatively with the experimental ultimate turbulence results shown by green squares. However, for the experimental results, the maximum of ![]() $Nu$ is attained at
$Nu$ is attained at ![]() $a\approx 0.3$ and, as noted in § 3, the Nusselt number scaling is
$a\approx 0.3$ and, as noted in § 3, the Nusselt number scaling is ![]() $Nu\propto Ta^{0.38}$. The Taylor vortex results naturally have a much smaller
$Nu\propto Ta^{0.38}$. The Taylor vortex results naturally have a much smaller ![]() $Nu$, because it is scaled like
$Nu$, because it is scaled like ![]() $Ta^{0.3}$ as the second peak seen in the
$Ta^{0.3}$ as the second peak seen in the ![]() $a=0$ case. In figure 16(b), we also plotted
$a=0$ case. In figure 16(b), we also plotted ![]() $K_1$ and
$K_1$ and ![]() $K_{\infty }$ obtained in the transitional state analysis (see (B5a,b) and (B7a,b) in Appendix B). Roughly speaking, the peaks occur when
$K_{\infty }$ obtained in the transitional state analysis (see (B5a,b) and (B7a,b) in Appendix B). Roughly speaking, the peaks occur when ![]() $k/Ta^{1/4}$ is approximately half of
$k/Ta^{1/4}$ is approximately half of ![]() $K_{\infty }$. The linear and nonlinear instabilities disappear at the Rayleigh line
$K_{\infty }$. The linear and nonlinear instabilities disappear at the Rayleigh line ![]() $a=-\eta ^2\approx -0.51$, which can be found from Rayleigh's stability condition.
$a=-\eta ^2\approx -0.51$, which can be found from Rayleigh's stability condition.

Figure 16. (a) The Nusselt number at ![]() $Ta=10^{10}$ for
$Ta=10^{10}$ for ![]() $\eta =5/7$. The red crosses are the Taylor vortex solution with the optimised wavenumbers shown in (b). The green squares are experimental results by Dennis et al. (Reference Dennis, Huisman, Bruggert, Sun and Lohse2011). (b) The red crosses are the local maximum of
$\eta =5/7$. The red crosses are the Taylor vortex solution with the optimised wavenumbers shown in (b). The green squares are experimental results by Dennis et al. (Reference Dennis, Huisman, Bruggert, Sun and Lohse2011). (b) The red crosses are the local maximum of ![]() $Nu$ closest to the bifurcation point. According to the asymptotic theory, the Taylor vortex solution bifurcates from circular Couette flow at
$Nu$ closest to the bifurcation point. According to the asymptotic theory, the Taylor vortex solution bifurcates from circular Couette flow at ![]() $K_1$ (see (B5a,b)). The Nusselt number
$K_1$ (see (B5a,b)). The Nusselt number ![]() $Nu$ is
$Nu$ is ![]() $O(1)$ when
$O(1)$ when ![]() $k/Ta^{1/4}\in (K_\infty, K_1)$, where
$k/Ta^{1/4}\in (K_\infty, K_1)$, where ![]() $K_{\infty }$ is given in (B7a,b). For
$K_{\infty }$ is given in (B7a,b). For ![]() $k/Ta^{1/4}< K_\infty$, the
$k/Ta^{1/4}< K_\infty$, the ![]() $Nu$ scaling is like the second peak state.
$Nu$ scaling is like the second peak state.
Brauckmann, Salewski & Eckhardt (Reference Brauckmann, Salewski and Eckhardt2016) and Brauckmann & Eckhardt (Reference Brauckmann and Eckhardt2017) reported that when the gap is narrow, there are two values of ![]() $R_{\varOmega }=(1-\eta )({R_i+R_o})/({R_i-\eta R_o})$ at which the local maximum of
$R_{\varOmega }=(1-\eta )({R_i+R_o})/({R_i-\eta R_o})$ at which the local maximum of ![]() $Nu$ occurs. Whether similar results can be obtained with the Taylor vortex solution is left for future work.
$Nu$ occurs. Whether similar results can be obtained with the Taylor vortex solution is left for future work.
7. Conclusions and discussion
In this study, the Taylor vortex solution branch is continued to very high Taylor numbers, and a theoretical rationale is given for its asymptotic properties. The limiting behaviour of the solution depends on how the axial period of the solution ![]() $2{\rm \pi} /k$ is scaled by
$2{\rm \pi} /k$ is scaled by ![]() $Ta$. The range of
$Ta$. The range of ![]() $k$ from
$k$ from ![]() $O(1)$ to the value where it is so large that the nonlinear solution ceases to exist is covered in the analysis. The Taylor vortex solution with a wavenumber
$O(1)$ to the value where it is so large that the nonlinear solution ceases to exist is covered in the analysis. The Taylor vortex solution with a wavenumber ![]() $k$ of
$k$ of ![]() $O(1)$ reproduces surprisingly well the properties of the large-scale coherent structures in the classical turbulence regime. The numerical results also suggest that there may be some connection between the onset of the ultimate turbulence regime and the high-wavenumber solutions, although the precise role of the solutions in the dynamics needs to be clarified in the future.
$O(1)$ reproduces surprisingly well the properties of the large-scale coherent structures in the classical turbulence regime. The numerical results also suggest that there may be some connection between the onset of the ultimate turbulence regime and the high-wavenumber solutions, although the precise role of the solutions in the dynamics needs to be clarified in the future.
Our results provide evidence that the strategy of taking a simple solution from the dynamics and applying the matched asymptotic expansion for it can be used even for fully developed high-Reynolds-number turbulence to some extent. This finding offers great hope for the first principles explanation for turbulent momentum and heat transport that is still poorly understood.
7.1. Summary of the asymptotic properties of the solutions
When ![]() $k=O(1)$, the asymptotic solution consists of an inviscid core and a viscous boundary layer enveloping it. In the core region, the Prandtl–Batchelor theorem imposes strong restrictions on the structure of the flow field. The asymptotic scaling of the wind Reynolds number
$k=O(1)$, the asymptotic solution consists of an inviscid core and a viscous boundary layer enveloping it. In the core region, the Prandtl–Batchelor theorem imposes strong restrictions on the structure of the flow field. The asymptotic scaling of the wind Reynolds number ![]() $Re_w=O(Ta^{1/2})$ is consistent with the turbulent observations (Huisman et al. Reference Huisman, van Gils, Grossmann, Sun and Lohse2012; Ostilla et al. Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013). On the other hand, the viscous boundary layer can be divided into a wall boundary layer and a plume. According to the asymptotic analysis, it is the Coriolis force acting on the plume that drives the overall flow. The theoretical Nusselt number for the
$Re_w=O(Ta^{1/2})$ is consistent with the turbulent observations (Huisman et al. Reference Huisman, van Gils, Grossmann, Sun and Lohse2012; Ostilla et al. Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013). On the other hand, the viscous boundary layer can be divided into a wall boundary layer and a plume. According to the asymptotic analysis, it is the Coriolis force acting on the plume that drives the overall flow. The theoretical Nusselt number for the ![]() $k=O(1)$ solutions is
$k=O(1)$ solutions is ![]() $Nu=O(Ta^{1/4})$, and the DNS data suggest that the same
$Nu=O(Ta^{1/4})$, and the DNS data suggest that the same ![]() $Nu$ scaling can be applied for the classical turbulence.
$Nu$ scaling can be applied for the classical turbulence.
The Nusselt number of the solution reaches its maximum when ![]() $k=O(Ta^{2/9})$. This asymptotic state, which we call the first peak state, has a structure similar to the
$k=O(Ta^{2/9})$. This asymptotic state, which we call the first peak state, has a structure similar to the ![]() $k=O(1)$ flow in a neighbourhood of the walls. The near-wall boundary layer becomes thinner than the
$k=O(1)$ flow in a neighbourhood of the walls. The near-wall boundary layer becomes thinner than the ![]() $k=O(1)$ case, so naturally, the Nusselt number is increased. At the same time, viscous effects in the plume dominate Coriolis forces. This means that the Coriolis force must act in the core to drive the vortex, and this condition determines the scaling
$k=O(1)$ case, so naturally, the Nusselt number is increased. At the same time, viscous effects in the plume dominate Coriolis forces. This means that the Coriolis force must act in the core to drive the vortex, and this condition determines the scaling ![]() $Nu=O(Ta^{1/3})$ and
$Nu=O(Ta^{1/3})$ and ![]() $Re_w=O(Ta^{4/9})$. For large-wavenumber solutions, the radial velocity is much larger than the axial velocity, so the scaling of
$Re_w=O(Ta^{4/9})$. For large-wavenumber solutions, the radial velocity is much larger than the axial velocity, so the scaling of ![]() $Re_w$ is the same for the definitions used by Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) and Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013).
$Re_w$ is the same for the definitions used by Huisman et al. (Reference Huisman, van Gils, Grossmann, Sun and Lohse2012) and Ostilla et al. (Reference Ostilla, Stevens, Grossmann, Verzicco and Lohse2013).
There is another local maximum for the Nusselt number, which occurs at ![]() $k=O(Ta^{1/4})$. In this second peak state, the nonlinear interaction of the axially fluctuating component disappears in the core. As a result, only a single Fourier mode and mean flow play a major role. To connect this core flow towards the cylinder walls, three near-wall layers are necessary. The bottom boundary layer adjacent to the cylinder wall is needed in order to satisfy the no-slip boundary conditions, and the top boundary layer must appear in order to attenuate the Fourier harmonics towards the core region. These two boundary layers of different natures can be matched through the middle boundary layer. The Nusselt number and wind Reynolds number scalings are
$k=O(Ta^{1/4})$. In this second peak state, the nonlinear interaction of the axially fluctuating component disappears in the core. As a result, only a single Fourier mode and mean flow play a major role. To connect this core flow towards the cylinder walls, three near-wall layers are necessary. The bottom boundary layer adjacent to the cylinder wall is needed in order to satisfy the no-slip boundary conditions, and the top boundary layer must appear in order to attenuate the Fourier harmonics towards the core region. These two boundary layers of different natures can be matched through the middle boundary layer. The Nusselt number and wind Reynolds number scalings are ![]() $O(Ta^{3/10})$ and
$O(Ta^{3/10})$ and ![]() $O(Ta^{2/5})$, respectively, ignoring a minor logarithmic correction. The Coriolis force is a leading-order effect in all regions except the bottom boundary layer.
$O(Ta^{2/5})$, respectively, ignoring a minor logarithmic correction. The Coriolis force is a leading-order effect in all regions except the bottom boundary layer.
The second peak state appears only when the scaled wavenumber ![]() $k\,Ta^{-1/4}$ is smaller than the critical value
$k\,Ta^{-1/4}$ is smaller than the critical value ![]() $K_{\infty }$, which can be determined analytically. As the wavenumber
$K_{\infty }$, which can be determined analytically. As the wavenumber ![]() $k$ is increased further, the Taylor vortex undergoes a transitional state similar to that analysed by Denier (Reference Denier1992) and then becomes a laminar flow. The Nusselt number of the transitional state is
$k$ is increased further, the Taylor vortex undergoes a transitional state similar to that analysed by Denier (Reference Denier1992) and then becomes a laminar flow. The Nusselt number of the transitional state is ![]() $O(Ta^0)$ and can be found analytically, which agrees well with the numerical results.
$O(Ta^0)$ and can be found analytically, which agrees well with the numerical results.
In summary, as ![]() $k$ is reduced from the linear critical point, the Taylor vortex solution develops according to the following scenario. First, vortices grow from near the inner cylinder in the transitional state. When the vortices reach the outer cylinder, the flow field becomes the second peak state. A further decrease in
$k$ is reduced from the linear critical point, the Taylor vortex solution develops according to the following scenario. First, vortices grow from near the inner cylinder in the transitional state. When the vortices reach the outer cylinder, the flow field becomes the second peak state. A further decrease in ![]() $k$ increases the thickness of the outer boundary layer, where Fourier harmonics are seen. The first peak state appears when the outer boundary layers on both sides come into contact. The axial scale of this state is sufficiently large for the separation of the inviscid region and the plume to be noticeable in the near-wall regions. When
$k$ increases the thickness of the outer boundary layer, where Fourier harmonics are seen. The first peak state appears when the outer boundary layers on both sides come into contact. The axial scale of this state is sufficiently large for the separation of the inviscid region and the plume to be noticeable in the near-wall regions. When ![]() $k=O(1)$, the inviscid region extends across the gap, and the scaling for the largest-scale vortices is established.
$k=O(1)$, the inviscid region extends across the gap, and the scaling for the largest-scale vortices is established.
How the above steady solutions relate to the turbulence dynamics is a natural question; Kooloth et al. (Reference Kooloth, Sondak and Smith2021) investigated this problem for two-dimensional RBC, and their results may also be applicable to our case. Their key observation is that local structures in the turbulent dynamics can be approximated by the relatively-short-wavelength solutions if the wavelength is chosen suitably. The detailed comparison of the dynamics and the solutions revealed that local structures with a wide range of wavelengths are embedded in turbulence. It is still unknown how often the solution of each wavelength appears in the dynamics. But if all solutions are equally likely to appear, then the solutions with the largest ![]() $Nu$ scaling will have greatest impact on the average value of
$Nu$ scaling will have greatest impact on the average value of ![]() $Nu$ in the dynamics.
$Nu$ in the dynamics.
An interesting aspect of the above asymptotic theories is that they show what the mean flow ![]() $\bar {v}$ in the core will look like. When
$\bar {v}$ in the core will look like. When ![]() $k$ is not too large, the mean angular momentum
$k$ is not too large, the mean angular momentum ![]() $r\bar {v}$ becomes a constant in the core region. In the
$r\bar {v}$ becomes a constant in the core region. In the ![]() $k=O(1)$ case, this is a consequence of the Prandtl–Batchelor theorem. The mean angular momentum profile becomes non-uniform when
$k=O(1)$ case, this is a consequence of the Prandtl–Batchelor theorem. The mean angular momentum profile becomes non-uniform when ![]() $k=O(Ta^{1/4})$, but instead, an analytical solution can be derived up to an unknown constant. The time-averaged turbulence data support the former uniform angular momentum law (Wattendorf Reference Wattendorf1935; Taylor Reference Taylor1935; Smith & Townsend Reference Smith and Townsend1982; Lewis & Swinney Reference Lewis and Swinney1999; Ostilla-Mónico et al. Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b). The fact that
$k=O(Ta^{1/4})$, but instead, an analytical solution can be derived up to an unknown constant. The time-averaged turbulence data support the former uniform angular momentum law (Wattendorf Reference Wattendorf1935; Taylor Reference Taylor1935; Smith & Townsend Reference Smith and Townsend1982; Lewis & Swinney Reference Lewis and Swinney1999; Ostilla-Mónico et al. Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b). The fact that ![]() $\bar {v}$ is proportional to
$\bar {v}$ is proportional to ![]() $1/r$ implies that the mean flow is irrotational. By taking the narrow gap limit, it can be seen that the argument here explains why zero absolute vorticity states are commonly found in rotating parallel shear flows (see Johnston, Halleen & Lezius Reference Johnston, Halleen and Lezius1972; Tanaka et al. Reference Tanaka, Kida, Yanase and Kawahara2000; Suryadi, Segalini & Alfredsson Reference Suryadi, Segalini and Alfredsson2014; Kawata & Alfredsson Reference Kawata and Alfredsson2016).
$1/r$ implies that the mean flow is irrotational. By taking the narrow gap limit, it can be seen that the argument here explains why zero absolute vorticity states are commonly found in rotating parallel shear flows (see Johnston, Halleen & Lezius Reference Johnston, Halleen and Lezius1972; Tanaka et al. Reference Tanaka, Kida, Yanase and Kawahara2000; Suryadi, Segalini & Alfredsson Reference Suryadi, Segalini and Alfredsson2014; Kawata & Alfredsson Reference Kawata and Alfredsson2016).
We further remark that the uniform angular momentum states are a natural generalisation of the uniform momentum states often observed in non-rotating shear flows. In particular, the staircase-like uniform momentum zones seen ubiquitously in the near-wall turbulent boundary layer have long attracted much attention (Meinhart & Adrian Reference Meinhart and Adrian1995; de Silva, Hutchins & Marusic Reference de Silva, Hutchins and Marusic2016). To explain this phenomenon, Montemuro et al. (Reference Montemuro, White, Klewicki and Chini2020) and Blackburn, Deguchi & Hall (Reference Blackburn, Deguchi and Hall2021) attempted to construct a theory for homogeneous shear flows. At the heart of these theories is the Prandtl–Batchelor theorem, which was first proposed to apply for the uniform momentum state by Deguchi & Hall (Reference Deguchi and Hall2014a) for a steady solution of plane Couette flow. However, it is not yet clear how such a core structure interacts with the near-wall flow and deduces the scaling of the momentum transport in the Reynolds number.
7.2. Link to the RBC studies
The asymptotic analyses of the first and second peaks presented in this paper can also be applied to the roll cell solutions of RBC (regardless of whether the boundary is slip or no-slip) and therefore provide a theoretical explanation for the scaling obtained by the numerical computation in Waleffe et al. (Reference Waleffe, Boonkasame and Smith2015) and Sondak et al. (Reference Sondak, Smith and Waleffe2015). Note, however, that for RBC, the transitional state exists only in the vicinity of the bifurcation point in the parameter space (Blennerhassett & Bassom Reference Blennerhassett and Bassom1994). This is due to the fact that in RBC, the instability occurs uniformly in the flow, whereas in TCF, the centrifugal instability is usually most pronounced near the inner cylinder.
The computation of the roll cell solution branch by Wen et al. (Reference Wen, Goluskin and Doering2022) reaches ![]() $Ra=10^{14}$, which is close to the experimentally feasible limit. In their numerical result, the exponent for
$Ra=10^{14}$, which is close to the experimentally feasible limit. In their numerical result, the exponent for ![]() $k$ at the first peak is closer to
$k$ at the first peak is closer to ![]() $1/5$ than
$1/5$ than ![]() $2/9$. However, their
$2/9$. However, their ![]() $Nu$ exponent is also slightly off from
$Nu$ exponent is also slightly off from ![]() $1/3$, so a calculation with a larger
$1/3$, so a calculation with a larger ![]() $Ra$ would be necessary to obtain the exponents accurately. Of course, the possibility that an unknown asymptotic state exists cannot be ruled out, but it appears from the author's experience that it is difficult to construct new sensible asymptotic theories.
$Ra$ would be necessary to obtain the exponents accurately. Of course, the possibility that an unknown asymptotic state exists cannot be ruled out, but it appears from the author's experience that it is difficult to construct new sensible asymptotic theories.
It is worth mentioning that Iyer et al. (Reference Iyer, Scheel, Schumacher and Sreenivasan2020) obtained the Nusselt number exponents 0.29 and 0.331 for moderate and high Rayleigh number regimes, respectively, for RBC in a vertically elongated tank. These exponents are close to those of the second and first peaks. The scaling of the first peak matches with the so-called classical scaling, but our derivation differs significantly from that of Priestley (Reference Priestley1954), Malkus (Reference Malkus1954) and Grossmann & Lohse (Reference Grossmann and Lohse2000). Recently, Kawano et al. (Reference Kawano, Motoki, Shimizu and Kawahara2021) derived the scaling laws by considering the naive balance of each term in the governing equations within the boundary layer. Although they do not assume the two-dimensionality of the flow, the scaling is consistent with our first peak asymptotic state. In particular, the wind Reynolds number scaling ![]() $Re_w=O(Ta^{4/9})$ that we found is in agreement with the results by Grossmann & Lohse (Reference Grossmann and Lohse2000) and Kawano et al. (Reference Kawano, Motoki, Shimizu and Kawahara2021). As pointed out in the latter, the exponent
$Re_w=O(Ta^{4/9})$ that we found is in agreement with the results by Grossmann & Lohse (Reference Grossmann and Lohse2000) and Kawano et al. (Reference Kawano, Motoki, Shimizu and Kawahara2021). As pointed out in the latter, the exponent ![]() $4/9\approx 0.444$ is close to 0.458 observed in the high-Rayleigh-number DNS by Iyer et al. (Reference Iyer, Scheel, Schumacher and Sreenivasan2020). Their wind Reynolds number is defined by the root-mean-square of the three velocity components normalised by viscous velocity scale
$4/9\approx 0.444$ is close to 0.458 observed in the high-Rayleigh-number DNS by Iyer et al. (Reference Iyer, Scheel, Schumacher and Sreenivasan2020). Their wind Reynolds number is defined by the root-mean-square of the three velocity components normalised by viscous velocity scale ![]() $\nu /H$, where
$\nu /H$, where ![]() $H$ is the vertical length of the tank, and thus is comparable with our results. Iyer et al. (Reference Iyer, Scheel, Schumacher and Sreenivasan2020) used a computational domain where the horizontal scale is
$H$ is the vertical length of the tank, and thus is comparable with our results. Iyer et al. (Reference Iyer, Scheel, Schumacher and Sreenivasan2020) used a computational domain where the horizontal scale is ![]() $1/10$ of the vertical scale, and it therefore makes sense that the result is related to our large-
$1/10$ of the vertical scale, and it therefore makes sense that the result is related to our large-![]() $k$ solutions.
$k$ solutions.
The exponent of the Nusselt number obtained in Iyer et al. (Reference Iyer, Scheel, Schumacher and Sreenivasan2020) is smaller than the 0.38 obtained by He et al. (Reference He, Funfschilling, Nobach, Bodenschatz and Guenter2012). The tank aspect ratio might be one of the causes of this difference. However, there are only a few reports of ![]() $Nu$ exponents exceeding
$Nu$ exponents exceeding ![]() $1/3$ in RBC, and the true nature of ultimate RBC scaling is still a matter of active debate. Wen et al. (Reference Wen, Goluskin and Doering2022) summarised the
$1/3$ in RBC, and the true nature of ultimate RBC scaling is still a matter of active debate. Wen et al. (Reference Wen, Goluskin and Doering2022) summarised the ![]() $Nu$ data of turbulent RBC and found that they were all smaller than those of the optimised steady roll cell solution corresponding to the first peak state. Zhu et al. (Reference Zhu, Mathai, Stevens, Verzicco and Lohse2018) restricted the DNS of RBC to two dimensions, and increased the Rayleigh number to
$Nu$ data of turbulent RBC and found that they were all smaller than those of the optimised steady roll cell solution corresponding to the first peak state. Zhu et al. (Reference Zhu, Mathai, Stevens, Verzicco and Lohse2018) restricted the DNS of RBC to two dimensions, and increased the Rayleigh number to ![]() $10^{14}$, hoping to see the ultimate turbulence scaling. However, their numerical data are scaled by the exponent
$10^{14}$, hoping to see the ultimate turbulence scaling. However, their numerical data are scaled by the exponent ![]() $\beta =1/3$, as pointed out by Doering, Toppaladoddi & Wettlaufer (Reference Doering, Toppaladoddi and Wettlaufer2019). Even without restricting to two-dimensional steady states, the existence of simple solutions with an exponent greater than
$\beta =1/3$, as pointed out by Doering, Toppaladoddi & Wettlaufer (Reference Doering, Toppaladoddi and Wettlaufer2019). Even without restricting to two-dimensional steady states, the existence of simple solutions with an exponent greater than ![]() $1/3$ is still unknown. Motoki, Kawahara & Shimizu (Reference Motoki, Kawahara and Shimizu2021) computed a three-dimensional steady solution of RBC, but the
$1/3$ is still unknown. Motoki, Kawahara & Shimizu (Reference Motoki, Kawahara and Shimizu2021) computed a three-dimensional steady solution of RBC, but the ![]() $Nu$ scaling was similar to that seen in Waleffe et al. (Reference Waleffe, Boonkasame and Smith2015) and Sondak et al. (Reference Sondak, Smith and Waleffe2015).
$Nu$ scaling was similar to that seen in Waleffe et al. (Reference Waleffe, Boonkasame and Smith2015) and Sondak et al. (Reference Sondak, Smith and Waleffe2015).
7.3. What is missing in the theoretical results?
Unlike RBC, the emergence of the Nusselt number exponent ![]() $\beta =0.38$ is well-established in the ultimate turbulence regime of TCF. Therefore, the predictions by the first peak state should eventually deviate from the turbulent measurement as the Taylor number increases. In the ultimate turbulence, a mix of large-scale and small-scale structures was observed, so in a sense, it is natural that this difference should appear. Experiments have shown that large-scale structures with scaling
$\beta =0.38$ is well-established in the ultimate turbulence regime of TCF. Therefore, the predictions by the first peak state should eventually deviate from the turbulent measurement as the Taylor number increases. In the ultimate turbulence, a mix of large-scale and small-scale structures was observed, so in a sense, it is natural that this difference should appear. Experiments have shown that large-scale structures with scaling ![]() $Re_w=Ta^{1/2}$ can be observed even in the ultimate turbulence regime (see Huisman et al. Reference Huisman, van Gils, Grossmann, Sun and Lohse2012). This suggests that the
$Re_w=Ta^{1/2}$ can be observed even in the ultimate turbulence regime (see Huisman et al. Reference Huisman, van Gils, Grossmann, Sun and Lohse2012). This suggests that the ![]() $k=O(1)$ state studied in § 4 still plays some role in the dynamics, but as we have seen in our analysis, it cannot transport angular momentum efficiently. The reason for the inefficiency is the Prandtl-Batchelor homogenisation of
$k=O(1)$ state studied in § 4 still plays some role in the dynamics, but as we have seen in our analysis, it cannot transport angular momentum efficiently. The reason for the inefficiency is the Prandtl-Batchelor homogenisation of ![]() $\varGamma$ as remarked just below (4.16). Thus it would be a natural idea to introduce small-scale vortices in the core to enhance transport. Note, however, that vortices of approximately Kolmogorov microscale
$\varGamma$ as remarked just below (4.16). Thus it would be a natural idea to introduce small-scale vortices in the core to enhance transport. Note, however, that vortices of approximately Kolmogorov microscale ![]() $Re_w^{-1/2}$ are unlikely to show any improvement. The typical velocity scale
$Re_w^{-1/2}$ are unlikely to show any improvement. The typical velocity scale ![]() $Re_w^{1/2}$ (see e.g. Deguchi Reference Deguchi2015) yields
$Re_w^{1/2}$ (see e.g. Deguchi Reference Deguchi2015) yields ![]() $O(\tilde {\varGamma }|_c)=O(Ta^{-1/2}\,Re_w^{1/2})$, so from the transport balance
$O(\tilde {\varGamma }|_c)=O(Ta^{-1/2}\,Re_w^{1/2})$, so from the transport balance ![]() $Nu=O(Re_w \tilde {\varGamma }|_c)$ derived by (4.16), the scaling remains
$Nu=O(Re_w \tilde {\varGamma }|_c)$ derived by (4.16), the scaling remains ![]() $Nu=O(Ta^{1/4})$. On the other hand, the azimuthal velocity perturbations generated by the first and second peak states are larger and may improve transport. If instead
$Nu=O(Ta^{1/4})$. On the other hand, the azimuthal velocity perturbations generated by the first and second peak states are larger and may improve transport. If instead ![]() $O(\tilde {\varGamma }|_c)=O(Ta^{-1/10})$ obtained in the second peak analysis is used, then the resultant scaling
$O(\tilde {\varGamma }|_c)=O(Ta^{-1/10})$ obtained in the second peak analysis is used, then the resultant scaling ![]() $Nu=O(Ta^{0.4})$ is close to the experimental observation, though of course it is not known whether such a flow structure is possible in the asymptotic expansion framework.
$Nu=O(Ta^{0.4})$ is close to the experimental observation, though of course it is not known whether such a flow structure is possible in the asymptotic expansion framework.
Another possible reason for the deviation of the ![]() $Nu$ scaling would be the axisymmetric restriction imposed for the Taylor vortex. When the three-dimensionality of TCF is allowed, feedback through Reynolds stresses appears from the non-axisymmetric component to the axisymmetric component. This feedback effect is a key process in self-sustaining the coherent structures in non-rotating shear flows (Waleffe Reference Waleffe1997), and recently Dessup et al. (Reference Dessup, Tuckerman, Wesfreid, Barkley and Willis2018) and Sacco, Verzicco & Ostilla-Mónico (Reference Sacco, Verzicco and Ostilla-Mónico2019) attempted to extend this idea to TCF. Our results suggest that the feedback is unimportant for classical turbulence, though it may not be so for ultimate turbulence.
$Nu$ scaling would be the axisymmetric restriction imposed for the Taylor vortex. When the three-dimensionality of TCF is allowed, feedback through Reynolds stresses appears from the non-axisymmetric component to the axisymmetric component. This feedback effect is a key process in self-sustaining the coherent structures in non-rotating shear flows (Waleffe Reference Waleffe1997), and recently Dessup et al. (Reference Dessup, Tuckerman, Wesfreid, Barkley and Willis2018) and Sacco, Verzicco & Ostilla-Mónico (Reference Sacco, Verzicco and Ostilla-Mónico2019) attempted to extend this idea to TCF. Our results suggest that the feedback is unimportant for classical turbulence, though it may not be so for ultimate turbulence.
Minor modifications to the theories obtained in this paper using the existing asymptotic results would not fully explain the scaling of the ultimate turbulence. For example, azimuthal and time-dependent waves can be incorporated into our axisymmetric asymptotic theories, using the method used in Hall & Sherwin (Reference Hall and Sherwin2010), but this does not change the ![]() $Nu$ scaling. The crux of this problem would be that all existing nonlinear asymptotic theories for shear flows hardly change the scaling of the wall shear rate from that for laminar flows.
$Nu$ scaling. The crux of this problem would be that all existing nonlinear asymptotic theories for shear flows hardly change the scaling of the wall shear rate from that for laminar flows.
Experiments and numerical simulations have shown that there is universality in the friction factor of various high-Reynolds-number shear flows (see e.g. Orlandi, Bernardini & Pirozzoli Reference Orlandi, Bernardini and Pirozzoli2015). No rational asymptotic theory has been found to explain this friction factor. If a new simple solution that reproduces the universal friction factor scaling can be found, then it might serve as an important hint for understanding the ultimate turbulence of TCF as well. For example, if one assumes the empirical Blasius friction law (friction factor ![]() $\propto Re^{-1/4}$), then it implies the emergence of a near-wall boundary layer of thickness
$\propto Re^{-1/4}$), then it implies the emergence of a near-wall boundary layer of thickness ![]() $O(Re^{-3/4})$. In terms of the Taylor number, the boundary layer thickness is
$O(Re^{-3/4})$. In terms of the Taylor number, the boundary layer thickness is ![]() $O(Ta^{-3/8})$, so the Nusselt number exponent is
$O(Ta^{-3/8})$, so the Nusselt number exponent is ![]() $3/8=0.375$, which is not too far from 0.38. The similarities between the friction factor of TCF and other shear flows are also noted by Lathrop et al. (Reference Lathrop, Fineberg and Swinney1992). If the hypothesis that the ultimate turbulence of TCF shares a common mechanism with that of non-rotating shear flows is true, then this could settle the debate on whether the TCF–RBC analogy is valid in the extreme parameters.
$3/8=0.375$, which is not too far from 0.38. The similarities between the friction factor of TCF and other shear flows are also noted by Lathrop et al. (Reference Lathrop, Fineberg and Swinney1992). If the hypothesis that the ultimate turbulence of TCF shares a common mechanism with that of non-rotating shear flows is true, then this could settle the debate on whether the TCF–RBC analogy is valid in the extreme parameters.
Finally, we remark that the asymptotic structure discussed in this paper is valid when ![]() $R_i$ is smaller than or equal to
$R_i$ is smaller than or equal to ![]() $O(|R_o|)$, hence it does not cover the whole parameter space. When the cylinders are counter-rotating, on the neutral curve the scaling
$O(|R_o|)$, hence it does not cover the whole parameter space. When the cylinders are counter-rotating, on the neutral curve the scaling ![]() $R_i=O(|R_o|^{5/3})$ is established, as noted by Donnelly & Fultz (Reference Donnelly and Fultz1960) using a dimensional argument, by Esser & Grossmann (Reference Esser and Grossmann1996) using a heuristic extension of Rayleigh's stability condition, and by Deguchi (Reference Deguchi2016) using an asymptotic analysis. It is well known that non-axisymmetric disturbances are important near the neutral curve, and nonlinear patterns such as spirals and ribbons emerge. Furthermore, some solution branches can be continued in the subcritical parameter regime, and in this case non-axisymmetry of the flow is critically important to sustain the nonlinear flow; see Deguchi et al. (Reference Deguchi, Meseguer and Mellibovsky2014) and Wang et al. (Reference Wang, Ayats, Deguchi, Mellibovsky and Meseguer2022). Developing a nonlinear asymptotic theory capable of describing the above non-axisymmetric phenomena is another interesting idea for future work.
$R_i=O(|R_o|^{5/3})$ is established, as noted by Donnelly & Fultz (Reference Donnelly and Fultz1960) using a dimensional argument, by Esser & Grossmann (Reference Esser and Grossmann1996) using a heuristic extension of Rayleigh's stability condition, and by Deguchi (Reference Deguchi2016) using an asymptotic analysis. It is well known that non-axisymmetric disturbances are important near the neutral curve, and nonlinear patterns such as spirals and ribbons emerge. Furthermore, some solution branches can be continued in the subcritical parameter regime, and in this case non-axisymmetry of the flow is critically important to sustain the nonlinear flow; see Deguchi et al. (Reference Deguchi, Meseguer and Mellibovsky2014) and Wang et al. (Reference Wang, Ayats, Deguchi, Mellibovsky and Meseguer2022). Developing a nonlinear asymptotic theory capable of describing the above non-axisymmetric phenomena is another interesting idea for future work.
Acknowledgements
The author thanks Dr Ostilla-Mónico for sharing his DNS data, and Dr D. Goluskin for inspiring discussion.
Funding
This work was supported by Australian Research Council Discovery Project DP230102188.
Declaration of interests
The author reports no conflict of interest.
Appendix A. The narrow gap limits
First, we will derive the narrow gap limit of the Görtler type. Here, we focus on the stationary outer cylinder case studied by Denier (Reference Denier1992); see Deguchi (Reference Deguchi2016) for general cases. Before taking the limit, we rewrite the system (2.6) using ![]() $V=v/R_i$ and
$V=v/R_i$ and ![]() $y=r-r_i$. The boundary conditions become
$y=r-r_i$. The boundary conditions become
While taking the limit ![]() $\eta \rightarrow 1$, or equivalently
$\eta \rightarrow 1$, or equivalently ![]() $r_i\rightarrow \infty$, we assume that the transformed velocity components and their derivatives are all
$r_i\rightarrow \infty$, we assume that the transformed velocity components and their derivatives are all ![]() $O(r_i^0)$. Keeping
$O(r_i^0)$. Keeping ![]() $T=2R_i^2/r_i$ as
$T=2R_i^2/r_i$ as ![]() $O(r_i^0)$ to balance the Coriolis term, the limiting flow is governed by
$O(r_i^0)$ to balance the Coriolis term, the limiting flow is governed by
and ![]() $\partial _y u+\partial _z w=0$. Here,
$\partial _y u+\partial _z w=0$. Here, ![]() $\omega =\partial _z u-\partial _y w$,
$\omega =\partial _z u-\partial _y w$, ![]() $D=\partial _t+u\,\partial _y+w\,\partial _z$ and
$D=\partial _t+u\,\partial _y+w\,\partial _z$ and ![]() $\triangle =\partial _y^2+\partial _z^2$.
$\triangle =\partial _y^2+\partial _z^2$.
For the RPCF limit, on the other hand, the radial coordinate is shifted as ![]() $y=r-r_m$ so that the origin is at the mid-gap. Furthermore, we take the new azimuthal velocity
$y=r-r_m$ so that the origin is at the mid-gap. Furthermore, we take the new azimuthal velocity ![]() $V$ to satisfy
$V$ to satisfy ![]() $(v-v_b)=G(V+y)$, which means that a constant
$(v-v_b)=G(V+y)$, which means that a constant ![]() $G$ scales the disturbance. Here, we expect that the base flow of the transformed system becomes almost a linear profile when the gap is narrow. The boundary conditions become
$G$ scales the disturbance. Here, we expect that the base flow of the transformed system becomes almost a linear profile when the gap is narrow. The boundary conditions become
The constant ![]() $G$ is chosen as
$G$ is chosen as ![]() $G=-(rv_b)'/r$, and the key assumption to take the system to RPCF is
$G=-(rv_b)'/r$, and the key assumption to take the system to RPCF is ![]() $O(G)\ll O(v_b)$. Keeping
$O(G)\ll O(v_b)$. Keeping ![]() $T=2Gv_b(r_m)/r_m$ as
$T=2Gv_b(r_m)/r_m$ as ![]() $O(r_m^0)$, it is straightforward to show that in the narrow gap limit, the system (2.6) reduces to
$O(r_m^0)$, it is straightforward to show that in the narrow gap limit, the system (2.6) reduces to
and ![]() $\partial _y u+\partial _z w=0$. The derivation of RPCF here is mathematically simpler than the common one (see Drazin & Reid Reference Drazin and Reid1981), though the physical motivation would be a bit harder to see.
$\partial _y u+\partial _z w=0$. The derivation of RPCF here is mathematically simpler than the common one (see Drazin & Reid Reference Drazin and Reid1981), though the physical motivation would be a bit harder to see.
The assumption ![]() $O(G)\ll O(v_b)$ used in the RPCF limit is equivalent to
$O(G)\ll O(v_b)$ used in the RPCF limit is equivalent to ![]() $O(R_o-R_i)\ll O(R_i)$, meaning that the inner and outer cylinders rotate at approximately the same speed. Thus when considering a coordinate system rotating at the average speed of the cylinders, the Coriolis force acting on the fluid is uniform. The uniform force produces an effect equivalent to buoyancy, allowing us to use a perfect correspondence with RBC. Of course, in the general case this force is not uniform, which is why in the Denier case the instability grew from near the inner cylinder (see figure 14 also). Note that the forcing term in the general case corresponds to the third term on the right-hand side of (4.1b), and strictly speaking this is no longer a Coriolis force. In fact, the definition of the Coriolis force changes depending on which rotational coordinate system is chosen, hence it cannot be well-defined when the inner and outer cylinders rotate differentially. The forcing terms are produced by the change in the direction of the base flow (i.e. the linear terms in
$O(R_o-R_i)\ll O(R_i)$, meaning that the inner and outer cylinders rotate at approximately the same speed. Thus when considering a coordinate system rotating at the average speed of the cylinders, the Coriolis force acting on the fluid is uniform. The uniform force produces an effect equivalent to buoyancy, allowing us to use a perfect correspondence with RBC. Of course, in the general case this force is not uniform, which is why in the Denier case the instability grew from near the inner cylinder (see figure 14 also). Note that the forcing term in the general case corresponds to the third term on the right-hand side of (4.1b), and strictly speaking this is no longer a Coriolis force. In fact, the definition of the Coriolis force changes depending on which rotational coordinate system is chosen, hence it cannot be well-defined when the inner and outer cylinders rotate differentially. The forcing terms are produced by the change in the direction of the base flow (i.e. the linear terms in ![]() $r^{-1}v^2$ and
$r^{-1}v^2$ and ![]() $r^{-1}uv$ in (2.1)). They are not centrifugal forces either – centrifugal force can be included in the pressure gradient term and does not affect the dynamics.
$r^{-1}uv$ in (2.1)). They are not centrifugal forces either – centrifugal force can be included in the pressure gradient term and does not affect the dynamics.
The difference between the two limits also affects the azimuthal development of the flow, if any. For the Görtler-type limit, the scaling factor of the azimuthal velocity is large, therefore the flow must have a larger length scale than the gap in the azimuthal direction. In contrast, for the RPCF-type limit, we can make the scaling factor ![]() $G$ be
$G$ be ![]() $O(1)$ when
$O(1)$ when ![]() $R_i=O(r_m)$. In this case, the azimuthal length scale of the flow is comparable to the gap.
$R_i=O(r_m)$. In this case, the azimuthal length scale of the flow is comparable to the gap.
Appendix B. The transitional states with outer cylinder rotation
This appendix discusses what modifications are required if ![]() $\varGamma _o\neq 0$ in § 6.1. The effect of the outer cylinder rotation appears in the mean flow layer solution so that (6.2a,b) must be replaced by
$\varGamma _o\neq 0$ in § 6.1. The effect of the outer cylinder rotation appears in the mean flow layer solution so that (6.2a,b) must be replaced by
Noting that in the core we can still use (6.5) and (6.6), the continuity of ![]() $\bar {\varGamma }$ and
$\bar {\varGamma }$ and ![]() $r^3(r^{-2}\bar {\varGamma })_r$ at
$r^3(r^{-2}\bar {\varGamma })_r$ at ![]() $r=r_c$ is satisfied if
$r=r_c$ is satisfied if
 $$\begin{gather} \sqrt{\frac{A-r_c^4}{4T_0}}=B(r_o^2-r_c^2)+\varGamma_o, \end{gather}$$
$$\begin{gather} \sqrt{\frac{A-r_c^4}{4T_0}}=B(r_o^2-r_c^2)+\varGamma_o, \end{gather}$$
Eliminating ![]() $B$ from these equations we get
$B$ from these equations we get
which links ![]() $r_c^2$ and
$r_c^2$ and ![]() $T_0$.
$T_0$.
Now let us suppose ![]() $r_c=r_i$ when
$r_c=r_i$ when ![]() $T_0=T_1$ in the above equation. Then the scaled wavenumber at the linear critical point can be found easily as
$T_0=T_1$ in the above equation. Then the scaled wavenumber at the linear critical point can be found easily as
Likewise, setting ![]() $r_c=r_o$ and
$r_c=r_o$ and ![]() $T_0=T_{\infty }$ in (B4) gives
$T_0=T_{\infty }$ in (B4) gives
From this equation, the critical scaled wavenumber where ![]() $Nu$ blows up can be found as
$Nu$ blows up can be found as
 \begin{equation} K_{\infty}=T_{\infty}^{{-}1/4}, \quad T_{\infty}=\left \{\begin{array}{ll} \dfrac{r_o^4-r_i^4}{4(\varGamma_i^2-\varGamma_o^2)} & \text{if}\ \varGamma_i>\varGamma_o> 0,\\[14pt] \dfrac{r_o^4-r_i^4}{4\varGamma_i^2} & \text{if}\ \varGamma_o\leq 0. \end{array} \right .\end{equation}
\begin{equation} K_{\infty}=T_{\infty}^{{-}1/4}, \quad T_{\infty}=\left \{\begin{array}{ll} \dfrac{r_o^4-r_i^4}{4(\varGamma_i^2-\varGamma_o^2)} & \text{if}\ \varGamma_i>\varGamma_o> 0,\\[14pt] \dfrac{r_o^4-r_i^4}{4\varGamma_i^2} & \text{if}\ \varGamma_o\leq 0. \end{array} \right .\end{equation}
Note that (B6) may have two roots, but by assuming that ![]() $K_{\infty }(a)=T_{\infty }^{-1/4}$ is a continuous function and that
$K_{\infty }(a)=T_{\infty }^{-1/4}$ is a continuous function and that ![]() $K_{\infty }\rightarrow 0$ as the Rayleigh line (
$K_{\infty }\rightarrow 0$ as the Rayleigh line (![]() $\varGamma _i=\varGamma _o$) is approached, we can determine the solution (B7a,b) uniquely.
$\varGamma _i=\varGamma _o$) is approached, we can determine the solution (B7a,b) uniquely.
To find ![]() $N_0$, we use the fact that the quadratic equation
$N_0$, we use the fact that the quadratic equation
can be obtained by combining (B2), (B3) and (B4). The solution
 \begin{equation} N_0=2\frac{\sqrt{\varGamma_o^2+(A^{{-}1}r_o^4-1)\left(\varGamma_o^2+\dfrac{r_o^4}{4T_0}\right)} -\varGamma_o}{A^{{-}1}r_o^4-1} \end{equation}
\begin{equation} N_0=2\frac{\sqrt{\varGamma_o^2+(A^{{-}1}r_o^4-1)\left(\varGamma_o^2+\dfrac{r_o^4}{4T_0}\right)} -\varGamma_o}{A^{{-}1}r_o^4-1} \end{equation}and (6.1) yields
 \begin{equation} Nu(T_0)=\frac{(1+\eta)^4}{16\eta^3\sqrt{T_0}}\, \frac{r_i^4+4T_0\varGamma_i^2}{r_o^4-r_i^4-4T_0\varGamma_i^2} \left (\sqrt{\frac{r_o^4+4T_0\varGamma_o^2}{r_i^4+4T_0\varGamma_i^2}-1 } -\varGamma_o \right ), \end{equation}
\begin{equation} Nu(T_0)=\frac{(1+\eta)^4}{16\eta^3\sqrt{T_0}}\, \frac{r_i^4+4T_0\varGamma_i^2}{r_o^4-r_i^4-4T_0\varGamma_i^2} \left (\sqrt{\frac{r_o^4+4T_0\varGamma_o^2}{r_i^4+4T_0\varGamma_i^2}-1 } -\varGamma_o \right ), \end{equation}which is the generalised version of (6.17).