Hostname: page-component-5cf477f64f-mgq6s Total loading time: 0 Render date: 2025-04-04T09:13:02.202Z Has data issue: false hasContentIssue false
  • English
  • Français

On the detection of internal interfacial layers in turbulent flows

Published online by Cambridge University Press:  07 June 2019

Duosi Fan Open the ORCID record for Duosi Fan [Opens in a new window] ,
Jinglei Xu Open the ORCID record for Jinglei Xu [Opens in a new window] ,
Matthew X. Yao Open the ORCID record for Matthew X. Yao [Opens in a new window]  and
Jean-Pierre Hickey Open the ORCID record for Jean-Pierre Hickey [Opens in a new window]
Duosi Fan
Affiliation:
School of Energy and Power Engineering, Beihang University, Xueyuan Road, Beijing 100191, China Department of Mechanical and Mechatronics Engineering, University of Waterloo, University Avenue, Waterloo N2L 3G1, Canada
Jinglei Xu
Affiliation:
School of Energy and Power Engineering, Beihang University, Xueyuan Road, Beijing 100191, China Department of Mechanical and Mechatronics Engineering, University of Waterloo, University Avenue, Waterloo N2L 3G1, Canada
Matthew X. Yao
Affiliation:
Department of Mechanical and Mechatronics Engineering, University of Waterloo, University Avenue, Waterloo N2L 3G1, Canada
Jean-Pierre Hickey*
Affiliation:
Department of Mechanical and Mechatronics Engineering, University of Waterloo, University Avenue, Waterloo N2L 3G1, Canada
*
†Email address for correspondence: j6hickey@uwaterloo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

A novel approach to identify internal interfacial layers, or IILs, in wall-bounded turbulent flows is proposed. Using a fuzzy cluster method (FCM) on the streamwise velocity component, a unique and unambiguous grouping of the uniform momentum zones (UMZs) is achieved, thus allowing the identification of the IILs. The approach overcomes some of the key limitations of the histogram-based IIL identification methods. The method is insensitive to the streamwise domain length, can be used on inhomogeneous grids, uses all the available flow field data, is trivially extended to three dimensions and does not need user-defined parameters (e.g. number of bins) other than the number of zones. The number of zones for a given snapshot can be automatically determined by an a priori algorithm based on a kernel density estimation algorithm, or KDE. This automated approach is applied to compute the average number of UMZs as a function of Reynolds number 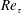$Re_{\unicode[STIX]{x1D70F}}$ in turbulent channel flows in several numerical simulations. This systematic approach reveals a dependence of the Reynolds number on the average number of UMZs in the channel flow; this supports previously reported observations in the boundary layer. The fuzzy clustering approach is applied to the turbulent boundary layer (experimental, planar particle image velocimetry) and channel flow (numerical, direct numerical simulation) at varying Reynolds numbers. The interfacial layers are characterized by a strong concentration of spanwise vorticity, with the outer-most layer located at the upper edge of the log layer. The three-dimensional interface identification reveals a streak-like organization. The large-scale motion (LSM) at the outer region of the channel flow boundary layer modulates the outer IIL. The corrugations of the outer IIL are aligned with the LSM and the conditional correlation of the inner and outer IIL height shows that extreme near-wall events leave their mark on the outer IIL corrugations.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 198 - 217
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Bezdek, J. C. 1974 Numerical taxonomy with fuzzy sets. J. Math. Biol. 1 (1), 57–71.Google Scholar
Bezdek, J. C. 1981 Objective function clustering. In Pattern Recognition with Fuzzy Objective Function Algorithms, pp. 43–93. Springer.Google Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.Google Scholar
Borrell, G. & Jiménez, J. 2016 Properties of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 801, 554–596.Google Scholar
Chauhan, K., Philip, J., de Silva, C. M., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.Google Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. Tech. Rep. Johns Hopkins University (NACA-TR-1244).Google Scholar
Del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Dunn, J. C. 1973 A fuzzy relative of the isodata process and its use in detecting compact well-separated clusters. Cybern. Syst. 3 (3), 32–57.Google Scholar
Eisma, J., Westerweel, J., Ooms, G. & Elsinga, G. E. 2015 Interfaces and internal layers in a turbulent boundary layer. Phys. Fluids 27 (5), 055103.Google Scholar
Friedman, J., Hastie, T. & Tibshirani, R. 2001 The Elements of Statistical Learning. Springer.Google Scholar
Hickey, J., Hussain, F. & Wu, X. 2013 Role of coherent structures in multiple self-similar states of turbulent planar wakes. J. Fluid Mech. 731, 312–363.Google Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106 (13), 134503.Google Scholar
Kolar, V. 2007 Vortex identification: new requirements and limitations. Intl J. Heat Fluid Flow 28 (4), 638–652.Google Scholar
Kwon, Y. S., Philip, J., de Silva, C. M., Hutchins, N. & Monty, J. P. 2014 The quiescent core of turbulent channel flow. J. Fluid Mech. 751, 228–254.Google Scholar
Lee, J., Lee, J. H., Choi, J.-I. & Sung, H. J. 2014 Spatial organization of large- and very-large-scale motions in a turbulent channel flow. J. Fluid Mech. 749, 818–840.Google Scholar
Lee, J., Sung, H. J. & Zaki, T. A. 2017 Signature of large-scale motions on turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 819, 165–187.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7 (4), 694–696.Google Scholar
Pal, N. R. & Bezdek, J. C. 1995 On cluster validity for the fuzzy c-means model. Trans. Fuz Syst. 3 (3), 370–379.Google Scholar
Pham, D. L., Xu, C. & Prince, J. L. 2000 Current methods in medical image segmentation. Annu. Rev. Biomed. Engng 2 (1), 315–337.Google Scholar
Saxton-Fox, T. & McKeon, B. J. 2017 Coherent structures, uniform momentum zones and the streamwise energy spectrum in wall-bounded turbulent flows. J. Fluid Mech. 826, R6.Google Scholar
Scott, D. W. 1992 Multivariate Density Estimation: Theory, Practice, and Visualization. John Wiley & Sons.Google Scholar
de Silva, C. M., Philip, J., Hutchins, N. & Marusic, I. 2017 Interfaces of uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 820, 451–478.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46 (1), 567–590.Google Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.Google Scholar
Silverman, B. W. 1998 Density Estimation for Statistics and Data Analysis. Routledge.Google Scholar
Tomkins, C. D.1997 A particle image velocimetry study of coherent structures in a turbulent boundary layer. Masters thesis, University of Illinois, Urbana.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent-nonturbulent interface of a jet. Phys. Rev. Lett. 95 (17), 174501.Google Scholar
Wu, X., Moin, P., Wallace, J. M., Skarda, J., Lozano-Durán, A. & Hickey, J.-P. 2017 Transitional–turbulent spots and turbulent–turbulent spots in boundary layers. Proc. Natl Acad. Sci. USA 114 (27), E5292–E5299.Google Scholar