2.1. Numerical methods and simulation parameters

The DNS discussed herein was generated using the ‘Miranda’ codebase, which has been employed in the past to investigate fundamental problems in turbulent mixing, such as the Rayleigh–Taylor and Richtmyer–Meshkov instabilities, among others (Cabot & Cook Reference Cabot and Cook2006; Olson et al. Reference Olson, Larsson, Lele and Cook2011; Tritschler et al. Reference Tritschler, Olson, Lele, Hickel, Hu and Adams2014). Miranda is formulated as an artificial large eddy simulation, which forgoes an explicit subgrid scale model in favour of dynamic fluid properties (e.g. viscosity, molecular diffusivity) that act only in the regions of steepest gradients (Cook Reference Cook2007). For the present simulation, the fluid diffusivities (namely viscosity, thermal conductivity and scalar diffusivity) are set to constant values. By ensuring that the smallest scales of flow are resolved by the grid spacing, the simulation discussed is a DNS.

Miranda solves the three-dimensional, compressible equations for conservation of mass ($\rho$), momentum ($\rho U_i$), energy ($E$) and scalar concentration ($\rho \varPhi$). Spatial derivatives are approximated with a tenth-order, compact finite difference scheme (Lele Reference Lele1992), and temporal integration is performed with a low-storage, five-stage, fourth-order Runge–Kutta scheme (Kennedy, Carpenter & Lewis Reference Kennedy, Carpenter and Lewis2000). An eighth-order compact filter, designed to remove approximately the top 10 % of wavenumbers, is used to dealias the solution at each time step. An adaptive time step, accounting for both advective and acoustic time scales, ensures proper temporal resolution and numerical stability. Interested readers are encouraged to consult Cook (Reference Cook2007, Reference Cook2009) for additional information on the code formulation.

This study is part of an ongoing project to port established computing software to heterogeneous architectures containing both traditional CPUs and graphics processing units (GPUs) at Lawrence Livermore National Laboratory (LLNL). More information regarding the GPU porting process can be found in the technical report by Anderson et al. (Reference Anderson2020).

The simulation presented herein is a canonical temporal mixing layer, with the initial mean velocity and passive scalar profiles initialized with the hyperbolic tangent function. The size of the computational domain is $L_x=1600\delta _0\times L_y=600\delta _0\times L_z=400\delta _0$, which is discretized by $4096\times 1536\times 1024$ (6.4 billion) grid points, and $\Delta x = \Delta y = \Delta z$. Boundary conditions are periodic in the $x,z$ (streamwise, spanwise) directions, with free-slip boundary in the $y$ (cross-stream) direction.

The initial Reynolds number based on the momentum thickness is ${Re}_{\delta _0} = \Delta U \delta _0/\upsilon = 120$, and the Schmidt and Prandtl numbers (for the passive scalar and thermal diffusivities) are set to $Sc=Pr=0.7$ to approximate atmospheric conditions. Homogeneous, isotropic velocity fluctuations are imposed on the mean velocity field to promote the growth of unstable modes and transition to turbulence; no fluctuations are added the mean scalar field. The convective Mach number $Ma = c_s/\Delta U$ is 0.15, such that compressibility effects can be neglected safely, and the fluid is effectively isothermal and incompressible.

In this configuration, the flow is statistically homogeneous in the $x,z$ directions, which implies that for any quantity $Q$, $\partial \langle Q\rangle /\partial x = \partial \langle Q\rangle /\partial z = 0$, where $\langle Q\rangle$ is the expected value of $Q$. From ergodic theory, the expected value can be estimated by spatial averaging over the two homogeneous directions, i.e.

(2.1)\begin{equation} \langle Q\rangle (y,t) = \frac{1}{L_xL_z}\int_{-L_x/2}^{L_x/2}\int_{-L_z/2}^{L_z/2}Q(x,y,z,t) \,{\rm d}\kern0.7pt x\,{\rm d}z , \end{equation}

and the Reynolds decomposition is used to define the fluctuating quantity $q(x,y,z,t) = Q(x,y,z,t) - \langle Q\rangle (y,t)$.

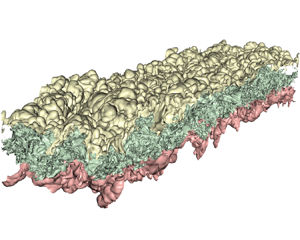
The computational domain used for the present study is displayed in figure 1, along with a snapshot of the passive scalar field at $t\,\Delta U/h_0=462$, where $h_0$ refers to the initial visual thickness of the velocity field, defined by (4.1). The blue colour represents $\varPhi =1$, and the white represents $\varPhi =0$. Arrows represent the direction of the mean flow. The $x,y$ plane shown is extracted at $z=0$, with the positive $z$ direction oriented out of the page.

Figure 1. Simple two-dimensional schematic of the mixing layer configuration, showcasing a snapshot of the scalar field at $t\,\Delta U/h_0=462$, during the self-similar evolution. Dark blue represents $\varPhi =1$, and white represents $\varPhi =0$.

To confirm that the grid spacing is adequately resolving the smallest scales of flow in the DNS, the ratio $\Delta x/\eta$ is computed and found to have a maximum value of $1.9$ during the transition to turbulence, with a value closer to $1.3$ during the self-similar period of evolution. Here,

(2.2)\begin{equation} \eta=(\upsilon^3/\varepsilon)^{1/4} \end{equation}

is the Kolmogorov scale, where the kinematic viscosity is $\upsilon =\mu /\rho$, the kinetic energy dissipation rate is $\varepsilon =2\upsilon \left \langle s_{ij}s_{ij} \right \rangle$, and $\eta$ is evaluated at the centreline of the mixing layer, corresponding to the maximum value of $\varepsilon$. According to Pope (Reference Pope2000), $\Delta x/\eta \leq 2.1$ is required to resolve the smallest scales of motion, suggesting that the current simulation is resolving fluid motion on the dissipation scale of the flow.

3.1. Standard iso-surface definitions

Consider a passive scalar field $\varPhi (x,y,z,t)$ that satisfies the advection–diffusion equation. An important related quantity is the diffusion velocity $w_{dif}$, which is a measure of the propagation speed of an iso-surface relative to the fluid in the direction of the surface normal $n_i$ (Gibson Reference Gibson1968). For incompressible flow of a passive scalar field, the diffusion velocity is given by

(3.1)\begin{equation} w_{dif} = \frac{D}{|\boldsymbol{\nabla} \varPhi|}\,\frac{\partial ^2\varPhi}{\partial x_i\partial x_i}, \end{equation}

in the direction normal to the iso-surface

(3.2)\begin{equation} n_i =-\frac{1}{|\boldsymbol{\nabla} \varPhi|}\,\frac{\partial \varPhi}{\partial x_i}, \end{equation}

where

(3.3)\begin{equation} |\boldsymbol{\nabla} \varPhi| = \left(\frac{\partial \varPhi}{\partial x_i}\,\frac{\partial \varPhi}{\partial x_i}\right)^{1/2}, \end{equation}

and summation is implied on repeated indices. In addition to $n_i$ and $w_{dif}$, an iso-surface can be characterized by its surface curvature,

(3.4)\begin{equation} \frac{\partial n_i}{\partial x_i} = k_1 + k_2, \end{equation}

where $k_1$ and $k_2$ are the principal curvatures of the iso-surface, and $\partial n_i/\partial x_i$ is equal to twice the mean curvature.

The area of an iso-surface is defined by Pope (Reference Pope1988) as

(3.5)\begin{equation} A_{iso} = \int_\mathcal{V} \varSigma' \,\mathrm{d}\mathcal{V}, \end{equation}

where $\mathcal {V}$ is an arbitrary volume, and $\varSigma '$ is the iso-surface area density,

(3.6)\begin{equation} \varSigma'=|\boldsymbol{\nabla} \varPhi|\,\delta(\varPhi-\varPhi_{iso}). \end{equation}

Here, $\varPhi _{iso}$ is the iso-value of $\varPhi$ pertaining to the surface, and $\delta ({\cdot })$ is the Dirac delta function (Vervisch et al. Reference Vervisch, Bidaux, Bray and Kollmann1995; Poinsot & Veynante Reference Poinsot and Veynante2005). The mean iso-surface area density $\varSigma$ is defined as

(3.7)\begin{equation} \varSigma = \left\langle |\boldsymbol{\nabla} \varPhi|\,\delta(\varPhi-\varPhi_{iso}) \right\rangle, \end{equation}

where $\left \langle {\cdot } \right \rangle$ denotes the expected value.

Based on (3.7), a transport equation for the mean surface area density $\varSigma$ can be derived (Trouvé & Poinsot Reference Trouvé and Poinsot1994; van Kalmthout & Veynante Reference van Kalmthout and Veynante1998):

(3.8)\begin{align} \frac{\partial \varSigma}{\partial t} = \underbrace{-\frac{\partial }{\partial x_i}\left(\left\langle U_i \right\rangle_s\varSigma\right)}_{\mathcal{T}_U} + \underbrace{\left\langle \frac{\partial U_i}{\partial x_i} - n_in_j\,\frac{\partial U_i}{\partial x_j} \right\rangle_s\varSigma}_{\mathcal{P}} \underbrace{{}-\frac{\partial }{\partial x_i}\left(\left\langle w_{dif} n_i \right\rangle_s\varSigma\right)}_{\mathcal{T}_D} + \underbrace{\left\langle w_{dif}\,\frac{\partial n_i}{\partial x_i} \right\rangle_s\varSigma}_{-\mathcal{D}}. \end{align}

The operator $\left \langle {\cdot } \right \rangle _s$ refers to a surface average, defined for an arbitrary property $Q$ by

(3.9)\begin{equation} \langle Q\rangle _s = \frac{\left\langle Q\varSigma' \right\rangle}{\varSigma}. \end{equation}

For convenience, the destruction term ${\mathcal {D}}$ has been defined with a leading negative sign due to the term taking on a negative value almost exclusively in the present data. From this definition, the equation for the iso-surface area density can be written simply as $\partial \varSigma /\partial t=\mathcal {T}_U + \mathcal {P} + \mathcal {T_D} - \mathcal {D}$. The terms in (3.8) refer to, in order, the rate of change of the mean iso-surface area density, $\partial \varSigma /\partial t$, the transport of $\varSigma$ due to the velocity field, $\mathcal {T}_U$, the rate of production of $\varSigma$ due to the flow strain rate, $\mathcal {P}$, the transport of $\varSigma$ due to molecular diffusion, $\mathcal {T}_D$, and the rate of destruction of $\varSigma$ due to the combined effects of molecular diffusion and surface curvature, $\mathcal {D}$. Note that although the current formulation assumes a passive scalar field that propagates via molecular diffusion, the effects of an active scalar field, such as a premixed flame surface, can be accounted for by including the effects of chemical reactions on the diffusion velocity in (3.1).

3.2. Iso-surface averaging in a mixing layer

Evaluating surface-weighted averages, especially for highly contorted surfaces such as those present in turbulent flows, is a challenging and nuanced problem. This study utilizes the same methodology described in the previous paper (Blakeley et al. Reference Blakeley, Olson and Riley2022, Appendix A) to evaluate iso-surface integrals, which is based on the work by Storti (Reference Storti2010) and Yurtoglu, Carton & Storti (Reference Yurtoglu, Carton and Storti2018). In essence, the approach yields a mathematically consistent approximation for $\varSigma '$, given in (3.6), for a discrete, implicitly defined scalar field on a uniform three-dimensional grid. The resulting field is a function of three-dimensional spatial coordinates $x$, $y$, $z$, and time $t$, and depends on the chosen iso-value $\varPhi _{iso}$. Note that $\varSigma '(x,y,z,t;\varPhi _{iso})$ contains mostly zero values; the function is non-zero only in the grid cells immediately adjacent to the iso-surface.

Using statistical homogeneity in the $x$ and $z$ directions, and ergodic theory, the mean surface area density $\varSigma$ is given by

(3.10)\begin{equation} \varSigma(y,t) = \frac{1}{L_xL_z (m\,\Delta y)}\int_{-L_x/2}^{L_x/2}\int_{y}^{y+(m\,\Delta y)}\int_{-L_z/2}^{L_z/2}\varSigma'(x,y,z,t)\,{\rm d}\kern0.7pt x\,{\rm d}y\,{\rm d}z, \end{equation}

where $m$ is an integer value that denotes the number of grid points included in the average in the $y$ direction. For $m=1$, this average reduces to the two-dimensional average defined in (2.1). In the present study, a value $m=16$ is used to reduce statistical fluctuations in the resulting $y$ profiles. From a physical standpoint, the mean iso-surface area density $\varSigma (y,t)$ can be interpreted as the average iso-surface area per unit volume contained in a slab of size $L_xL_z(m\,\Delta y)$, which is a function of the both the cross-stream direction $y$ and time $t$, and has units of $1/\text {length}$. The $y$ profiles of $\varSigma$ were compared for values of $m$ ranging from $1$ to $20$, and were found to be insensitive to the value of $m$ as long as $(m\,\Delta y)$ is small compared to the length scale of the mean flow.

Although the iso-surface average defined in (3.9) is utilized often in the literature, it can be poorly defined unless integrated over the entire iso-surface. In the case of the present DNS, it was found that the iso-surface area density $\varSigma (y,t)$ takes on a Gaussian-like profile that decays to zero away from its peak (refer to § 4). This means that, as given by (3.9), the iso-surface average $\langle Q\rangle _s$ is undefined near the edges of the mixing layer because $\varSigma \rightarrow 0$ as $y\rightarrow \pm L_y/2$. While the surface average is an intuitive concept, it is more practical to consider instead the weighted surface average

(3.11)\begin{equation} \langle Q\rangle _s\varSigma = \left\langle Q\varSigma ' \right\rangle = \frac{1}{L_xL_z(m\,\Delta y)}\int_{-L_x/2}^{L_x/2}\int_{y}^{y+(m\,\Delta y)}\int_{-L_z/2}^{L_z/2}Q\varSigma'\,{\rm d}\kern0.7pt x\,{\rm d}y\,{\rm d}z. \end{equation}

In fact, from inspection of (3.8), it can be seen that each of the terms on the right-hand side of the equation makes use of the weighted iso-surface average $\left \langle Q\varSigma ' \right \rangle$, rather than the iso-surface average $\langle Q\rangle _s$. As discussed above, the value of $m$ in the present study is set to $16$, which provides good statistical convergence. In addition, the data have been averaged in time to reduce statistical fluctuations, with averaging width approximately $8$ non-dimensional time units, $t\,\Delta U/h_0$. As will be shown below, the terms in (3.8) are expected to vary smoothly in time and space such that the averaging process described accurately retains the characteristic features of the flow.

In some cases, it is helpful to understand a quantity that has been averaged over the entire iso-surface contained in the computational domain. In these cases, the quantity can be evaluated by integrating the averaged quantity in the cross-stream direction. For example, the surface area of an iso-surface, $A_{iso}$, can be evaluated by

(3.12)\begin{equation} \frac{A_{iso}}{A_0} = \int_{-L_y/2}^{L_y/2}\varSigma\,{{\rm d}y}, \end{equation}

where $A_0=L_xL_z$ is the surface area at $t=0$.

5.1. Iso-surface area

Consider the integral of (3.8) over the cross-stream direction,

(5.1)\begin{equation} \frac{\mathrm{d}}{\mathrm{d}t}\int_{-Ly/2}^{Ly/2}\varSigma\,\mathrm{d} y =- \int_{-Ly/2}^{Ly/2}\left\langle n_in_jS_{ij} \right\rangle_s\varSigma\,\mathrm{d} y + \int_{-Ly/2}^{Ly/2}\left\langle w_{dif}\,\frac{\partial n_i}{\partial x_i} \right\rangle_s\varSigma\,\mathrm{d}y, \end{equation}

where the advective and diffusive transport terms are identically zero due to the zero flux boundary conditions, the production term has been simplified for constant density flow, and the time derivative has been moved outside the integral, assuming that the time derivative and the integration in $y$ commute. From (3.12) it can be shown that by integrating over the entire domain in $y$, the above equation describes the rate of change of iso-surface area ${\rm d}A_{iso}/{\rm d}t$, normalized by the surface area of a plane in the $x,z$ directions, $A_0=L_xL_z$. According to (5.1), the rate of change of iso-surface area is determined by the difference between the integrated production term $\int \mathcal {P}$ and the integrated destruction term $\int \mathcal {D}$, i.e. ${\rm d}A_{iso}/{\rm d}t = A_0(\int \mathcal {P} - \int \mathcal {D})$ (Wang Reference Wang2013).

The temporal evolutions of ${\rm d}A_{iso}/{\rm d}t$, $\int \mathcal {P}$ and $\int \mathcal {D}$ in (5.1) are plotted in figures 4(a,b) for $\varPhi _{iso}=0.5$ and $0.95$, respectively. An explicit finite difference approximation is used to estimate ${\rm d}A_{iso}/{\rm d}t$ from the DNS data. Note that this is a somewhat inaccurate approximation, as these quantities were calculated during post-processing using restart files that were saved once every 200 physical time steps, which degrades the temporal accuracy of the finite difference approximation. The lack of temporal resolution is evidenced clearly by the discrepancy between the direct approximation of ${\rm d}A_{iso}/{\rm d}t$ (dotted line) with the rate of change implied from the right-hand side of (5.1) (blue circles), especially early in the simulation, $t\,\Delta U/h_0 < 200$. Nonetheless, in the self-similar region, $t\,\Delta U/h_0>250$, the left-hand and right-hand sides of (5.1) are in approximate balance.

Figure 4. Temporal evolution of terms in the iso-surface area transport equation (5.1), for (a) $\varPhi _{iso} = 0.5$ and (b) $\varPhi _{iso} = 0.95$, non-dimensionalized by $h_0/\Delta U$. Blue circles indicate ${\rm d}A_{iso}/{\rm d}t$, green up-triangles indicate $\int \mathcal {P}$, purple down-triangles indicate $\int \mathcal {D}$ and $\int \mathcal {P} - \int \mathcal {D}$ is given by a dotted line. Additionally, the non-dimensional, integrated dissipation rates of kinetic energy and scalar variance, $\mathcal {E}/\Delta U^3$ and $\mathcal {X}/(\Delta U\,\Delta \varPhi ^2)$, have been scaled by constant values and are plotted as dashed and dash-dotted lines, respectively. Note the difference in scales between (a) and (b).

The steep growth of $A_{iso}$ during the transition to turbulence can be identified in figure 4 as a small peak in the evolution of ${\rm d}A_{iso}/{\rm d}t$, but more clearly as a steep increase in the magnitude of both terms $\int \mathcal {P}$ and $\int \mathcal {D}$ around $t\,\Delta U/h_0\approx 100$. In this transitional period, the magnitude of term $\int \mathcal {D}$ lags slightly behind term $\int \mathcal {P}$, resulting in the initial growth of surface area.

Notably, the evolutions of terms $\int \mathcal {P}$ and $\int \mathcal {D}$ are approximately proportional to the integrated dissipation rates of turbulent kinetic energy and scalar variance, defined as

(5.2)\begin{equation} \mathcal{E} = \int^{L_y/2}_{-L_y/2}\varepsilon\,{{\rm d} y} \end{equation}

and

(5.3)\begin{equation} \mathcal{X} = \int^{L_y/2}_{-L_y/2}\chi\,{{\rm d}y}, \end{equation}

respectively (Rogers & Moser Reference Rogers and Moser1994; Baltzer & Livescu Reference Baltzer and Livescu2020).The integrated dissipation rates $\mathcal {E}$ and $\mathcal {X}$, multiplied by constants $c_1$ and $-c_2$, respectively, are displayed in figure 4 as dashed and dash-dotted lines. The constant values are chosen empirically to highlight the similarity between the temporal evolution of the integrated dissipation rates and the integrated rates of production and destruction of iso-surface area. The values of $c_1$ and $c_2$ are constant in time but range from ${\approx } 5$ to $150$, depending on the value of $\varPhi _{iso}$.

The similarity between $\int \mathcal {P}$ and $\mathcal {E}$ is expected from previous models of flame surface area, which typically assume that $\int \mathcal {P}\sim (\varepsilon /\upsilon )^{1/2}$ or $\int \mathcal {P}\sim \varepsilon /k$ (see Poinsot & Veynante (Reference Poinsot and Veynante2005) for an overview). The near-symmetric behaviour of the production $\int \mathcal {P}$ and destruction $\int \mathcal {D}$ would suggest that the destruction is also linked to the kinetic energy dissipation rate $\mathcal {E}$. In the present DNS, there is also a strong relationship between the scalar dissipation rate $\mathcal {X}$ and both the production and destruction of iso-surface area, which is expected from the relationship between $\varSigma$ and $\varPhi$. Interestingly, for $\varPhi _{iso}=0.95$, there is better qualitative agreement between $\int \mathcal {P}$ and the scalar dissipation rate $\mathcal {X}$ during the transitions to turbulence, i.e. $t\,\Delta U/h_0<100$.

During the self-similar period ($t\,\Delta U/h_0 > 250$), the production and destruction terms are significantly larger than their difference, which is consistent with previous studies of iso-surface area transport (Han & Huh Reference Han and Huh2008; Blakeley et al. Reference Blakeley, Wang and Riley2019; Neamtu-Halic et al. Reference Neamtu-Halic, Krug, Mollicone, Reeuwijk, Haller and Holzner2020; Kulkarni & Bisetti Reference Kulkarni and Bisetti2021). This, coupled with the similarity to $\mathcal {E}$ and $\mathcal {X}$ above, might suggest that the total iso-surface area is independent of the mixing layer width, i.e. is constant in time. Interestingly, this does not tell the whole story; ${\rm d}A_{iso}/{\rm d}t$ is small, but not zero, during the self-similar period of evolution, as evidenced by the slight but noticeable increase of $A_{iso}$ over time in figure 3(a). In the following subsections, this seeming discrepancy will be investigated in more detail.

5.2. Iso-surface area density

Consider now the mean iso-surface area density transport, given by (3.8), subject to the iso-surface averaging methods discussed in § 3.2. The rate of change of iso-surface area density is determined by the production and destruction of $\varSigma$ as discussed previously, as well as advective and diffusive transport, i.e. $\partial \varSigma /\partial t = \mathcal {T}_U + \mathcal {P} + \mathcal {T}_D - \mathcal {D}$. Similar to arguments in the previous subsection, an estimate of $\partial \varSigma /\partial t$ is obtained via an explicit finite difference approximation of the $\varSigma (y,t)$ profiles, computed from the DNS data. Note that due to storage constraints, the full three-dimensional DNS fields are available only every 200 physical time steps, significantly limiting the temporal accuracy of the approximation. Nonetheless, it is a useful tool to determine the overall behaviour of the time derivative of $\varSigma$, and to test the accuracy of the results by comparing the time derivative to the right-hand side of the equation.

Cross-stream profiles of each term are displayed in figures 5(a,c) at $t\,\Delta U/h_0=462$ for $\varPhi _{iso} = 0.5$ and $0.95$, respectively. The terms have been non-dimensionalized by the mixing layer width and the velocity difference $\Delta U/h^2$. It can be seen that, similar to the results of figure 4, $\mathcal {P}$ and $\mathcal {D}$ are significantly larger than the remaining terms in the balance equation. Indeed, for $\varPhi _{iso}=0.5$, $\mathcal {P}$ and $\mathcal {D}$ are a full order of magnitude larger than $\partial \varSigma /\partial t$.

Figure 5. Cross-stream profiles of each term in (3.8), for (a,b) $\varPhi _{iso}=0.5$ and (c,d) $\varPhi _{iso}=0.95$, at a non-dimensional time at $t\,\Delta U/h_0=462$. Blue circles indicate $\partial \varSigma /\partial t$, orange squares indicate $\mathcal {T}_U$, green up-triangle indicate $\mathcal {P}$, red pentagons indicate $\mathcal {T_D}$, purple down-triangles indicate $\mathcal {D}$ and turquoise diamonds indicate $K$, where $K$ is given by (5.4). The dotted brown line is the sum of the terms on the right-hand side of (3.8). Note the difference in scales between (a,b) and between (c,d).

Rather than plotting $\mathcal {P}$ and $\mathcal {D}$ separately, consider instead the net effect of the production and destruction terms,

(5.4)\begin{equation} K = \mathcal{P} - \mathcal{D} =- \left\langle n_in_jS_{ij} \right\rangle_s\varSigma + \left\langle w_{dif}\, \frac{\partial n_i}{\partial x_i} \right\rangle_s\varSigma, \end{equation}

where $K$ has been described in the literature as the ‘net surface stretch’ (Candel & Poinsot Reference Candel and Poinsot1990; Kulkarni et al. Reference Kulkarni, Buttay, Kasbaoui, Attili and Bisetti2021). The net surface stretch K is plotted in figures 5(b,d) in place of $\mathcal{P}$ and $\mathcal{D}$ for the same time and iso-values as in figures 5(a,c). This comparison demonstrates that the difference between the production and destruction terms is of the same order of magnitude as $\partial \varSigma /\partial t$ and the advective transport $\mathcal {T}_U$; the diffusive transport term $\mathcal {T}_D$ is an order of magnitude smaller still. This has significant implications when estimating the self-similar evolution of each term, as described in the following sections.

The comparison between the left-hand and right-hand sides of (3.8) is included in figure 5 to give some idea of the accuracy of the numerical methodology used in the present study. To the authors’ knowledge, few (if any) studies have been able to compare directly the left-hand and right-hand sides of the iso-surface transport equation in a turbulent flow, due in part to the computational demand of traditional iso-surface integration methods and the temporal resolution required to estimate time derivatives. There is general agreement between the two sides of the equation, although some discrepancy exists between the temporal derivative of $\varSigma$ near $y=0$ compared to the right-hand side (see figure 5b). It is expected that this error is caused mainly by taking the difference between two large quantities, $\mathcal {P}$ and $\mathcal {D}$, each with its own errors, which are then magnified in computing this difference. Note the difference in scale between figures 5(a,b). Also note that there is considerably less discrepancy between the left-hand and right-hand sides near the boundary of the mixing layer (shown in figure 5d), where terms $\mathcal {P}$ and $\mathcal {D}$ are not nearly as large.

6.1. Rate of change of iso-surface area density

The self-similar behaviour of $\partial \varSigma /\partial t$ is examined in the context of the self-similar behaviour of $\varSigma$, which was suggested recently by Blakeley et al. (Reference Blakeley, Olson and Riley2022) to be

(6.1)\begin{equation} \varSigma(y,t) = \frac{1}{\lambda_\phi(t)}\,\hat{\varSigma}(\xi). \end{equation}

Therefore, the time derivative of $\varSigma$ can be expressed as

(6.2)\begin{equation} \frac{\partial \varSigma}{\partial t}(y,t) =-\frac{1}{h\lambda_\phi}\,\frac{{\rm d}h}{{\rm d}t}\,\frac{{\rm d}\hat{\varSigma}}{{\rm d}\xi}\,\xi -\frac{1}{\lambda_\phi^2}\,\frac{{\rm d}\lambda_\phi}{{\rm d}t}\,\hat{\varSigma}. \end{equation}

Focusing only on the dimensional coefficient of the first term (for now), the following self-similar scaling is proposed:

(6.3)\begin{equation} \frac{\partial \varSigma}{\partial t} = \frac{\Delta U}{h\lambda_\phi}\,\widehat{\frac{\partial \varSigma}{\partial t}}, \end{equation}

where

(6.4)\begin{equation} \widehat{\frac{\partial \varSigma}{\partial t}} = \frac{{\rm d}\hat{\varSigma}}{{\rm d}\xi}\,\xi - \hat{\varSigma} \end{equation}

will be used as shorthand notation for the self-similar form of the time derivative of $\varSigma$. Note that the velocity difference $\Delta U$ has been substituted in place of ${\rm d}h/{\rm d}t$ because it of its ubiquity in self-similar arguments from the literature (despite the fact that ${\rm d}h/{\rm d}t$ is arguably a more appropriate metric; Baltzer & Livescu Reference Baltzer and Livescu2020). Due to the linear development of $h$ in the self-similar region, $\Delta U$ and ${\rm d}h/{\rm d}t$ are proportional to each other in the present simulation.

Several instantaneous profiles of ${\rm d}\varSigma/{\rm d}t$ are plotted in figure 6. The instantaneous profiles are spatially averaged as in (2.1), non-dimensionalized by $h\lambda_\phi/U$, and compared to the average value over the entire self-similar period. For $\varPhi _{iso}=0.95$, the $y$ profiles appear to collapse onto the self-similar average. For the iso-value $\varPhi _{iso}=0.5$, however, the self-similar collapse is not as good, with significant fluctuations observed around the mean profile. Note that from the symmetry in the problem initial conditions, these curves should be symmetric about $y/h = 0$; this lack of symmetry gives an idea of the statistical error in the measurement. As discussed above, this error is expected to be caused by the limited temporal resolution available to be used in the numerical approximation of $\partial \varSigma /\partial t$.

Figure 6. Proposed self-similar scaling of $\partial \varSigma /\partial t$ from (3.8), conditioned on (a) $\varPhi _{iso}=0.5$ and (b) $\varPhi _{iso}=0.95$, as functions of the similarity variable $\xi =y/h$. The solid line refers to the time average over the entire self-similar period, and dashed lines refer to instantaneous profiles, spatially averaged as in (2.1).

Consider now the second term on the right-hand side of (6.2), which is expected to exhibit the same scaling properties as the first term on the right-hand side. Beginning from (4.8), the self-similar scaling of the scalar Taylor length scale is expected to be $\lambda _\phi \sim (hD/\Delta U)^{1/2}$, based on the self-similar scalings of $\left \langle \phi ^2 \right \rangle$ and $\chi$. Substituting this scaling for $\lambda _\phi$ into the second term on the right-hand side of (6.2) yields the expression

(6.5)\begin{equation} \frac{1}{\lambda_\phi^2}\,\frac{{\rm d}\lambda_\phi}{{\rm d}t} \sim \frac{\Delta U}{hD}\left(\frac{D}{\Delta U}\right)^{1/2}\frac{h^{-1/2}}{2}\,\frac{\mathrm{d}h}{\mathrm{d}t} \sim \frac{\Delta U}{h}\left(\frac{\Delta U}{hD}\right)^{1/2}\sim\frac{\Delta U}{h\lambda_\phi}, \end{equation}

which is identical to the self-similar scaling found in (6.3).

Importantly, the above scaling argument also suggests that the self-similar development of $\lambda _\phi$ is proportional to $h^{1/2}$, which can also be verified by the DNS data. The temporal evolution of $\lambda _\phi h^{-1/2}$ is plotted in figure 7(a) and can be seen to approach a constant value in the self-similar period, consistent with the proposed scaling argument. In addition to $\lambda _\phi$, the transverse Taylor and Kolmogorov scales are also plotted with the appropriate self-similar scaling applied.

Figure 7. (a) Self-similar development of Taylor and Kolmogorov microscales compared to predictions from self-similarity. (b,c) Self-similar profile of $\partial \varSigma /\partial t$ normalized by $h\lambda _\phi /\Delta U$ compared to the predicted self-similar profile assuming that $\varSigma$ is Gaussian (dashed line) and the sum of terms on the right-hand side of (3.8) (dotted line) for (b) $\varPhi _{iso}=0.5$ and (c) $\varPhi _{iso}=0.95$.

To further test the assumed self-similar form for the profile of $\partial \varSigma /\partial t$, it is compared to the right-hand side of (3.8), normalized by $h\lambda _\phi /\Delta U$, in figure 7. The self-similar profiles of the right-hand side of (3.8) (dotted line) demonstrate the correct behaviour for both iso-values plotted, although there are significant differences near the peaks of the curves for $\varPhi = 0.5$. This is similar to what was seen in figures 5(b,d).

As a second test, an approximation from a previous study (Blakeley et al. Reference Blakeley, Olson and Riley2022) can be leveraged to study the self-similar development of $\partial \varSigma /\partial t$. For the temporal mixing layer presented here, $\hat {\varSigma }$ can be approximated with a Gaussian profile, i.e.

(6.6)\begin{equation} \hat{\varSigma}(\xi;\varPhi_{iso}) = \hat{\varSigma}_m\exp\left(-\frac{(\xi-\xi_m)^2}{2\hat{\sigma}^2}\right), \end{equation}

where $\hat {\varSigma }_m$, $\xi _m$ and $\hat {\sigma }$ are the peak value, location of peak value and standard deviation of $\hat {\varSigma }$ in the self-similar coordinates (Blakeley et al. Reference Blakeley, Olson and Riley2022). Substituting the above expression for $\hat {\varSigma }(\xi )$ into (6.2), and using the values of $h$, ${\rm d}h/{\rm d}t$, $\lambda _\phi$ and ${\rm d}\lambda _\phi /{\rm d}t$ from the present DNS, yields the dashed line in figures 7(b,c). The behaviour of the Gaussian model is qualitatively correct, although there are discrepancies near the peaks of the curve.

6.2. Advective transport

Next, consider $\mathcal {T}_U = -(\partial /\partial x_i)(\left \langle U_i \right \rangle _s\varSigma )$, which describes the transport of $\varSigma$ due to the velocity field. This can be decomposed into mean and fluctuating components $\mathcal {T}_m$ and $\mathcal {T}_t$:

(6.7)\begin{equation} \frac{\partial }{\partial x_i}\left(\left\langle U_i \right\rangle_s\varSigma\right) = \underbrace{\frac{\partial }{\partial x_i}\left(\left\langle U_i \right\rangle\varSigma\right)}_{\mathcal{T}_m} + \underbrace{\frac{\partial }{\partial x_i}\left(\left\langle u_i \right\rangle_s\varSigma\right)}_{\mathcal{T}_t}, \end{equation}

where $\left \langle u_i \right \rangle _s$ is the surface average of the fluctuating component of velocity $u_i$. Due to the geometry of the mixing layer, only the cross-stream velocity $V$ will contribute to $\mathcal {T}_U$. Furthermore, it can be shown from conservation of mass and the free-slip boundary conditions that the mean cross-stream velocity, $\left \langle V \right \rangle$, must be zero for all values of $y$. Thus the effect of the velocity field on the rate of change of $\varSigma$ is due entirely to the turbulent fluctuations of the cross-stream velocity $v$, and hence the turbulent flux $\mathcal {T}_t$.

To estimate how $\mathcal {T}_t$ will evolve in the self-similar region, it is reasonable to assume that the surface-averaged velocity fluctuations $\left \langle u_i \right \rangle _s$ will scale similar to the root mean square (r.m.s.) velocity $\left \langle u_iu_i \right \rangle ^{1/2}$, which is known to scale with the velocity difference $\Delta U$ (Rogers & Moser Reference Rogers and Moser1994). By noting that $\varSigma \sim \lambda _\phi$ (see figures 3b,c) and assuming that the cross-stream derivative will scale with the mixing width, i.e. $\partial /\partial y\sim 1/h$, the self-similar form of $\mathcal {T}_t$ should be

(6.8)\begin{equation} \mathcal{T}_t = \frac{\Delta U}{h\lambda_\phi}\,\hat{\mathcal{T}}_t. \end{equation}

The proposed scaling for $\mathcal {T}_t$ results in a collapse of the instantaneous profiles on the self-similar form for $\partial \varSigma /\partial t$ in (6.3), suggesting that the scaling is consistent with the DNS data. Additionally, these results agree with the findings from Kulkarni & Bisetti (Reference Kulkarni and Bisetti2021), who found that the turbulent transport term (normalized by $\varSigma$) scales with the integral length scale of the flow.

The self-similar profiles of $\mathcal {T}_t$ are plotted in figure 8. Apart from small fluctuations around the peaks of the curves, the instantaneous profiles collapse onto a single curve for the assumed self-similar form, suggesting that (6.8) is the appropriate scaling for $\mathcal {T}_t$ for this temporal turbulent mixing layer.

Figure 8. Proposed self-similar scaling of term $\mathcal{T}_t = (\partial/\partial x_i) (\langle u_i\rangle_s\varSigma)$ from (6.8), conditioned on (a) $\varPhi _{iso}=0.5$ and (b) $\varPhi _{iso}=0.95$, as functions of the similarity variable $\xi =y/h$. Solid and dashed lines are as in figure 6.

These data also suggest that the turbulent transport for the iso-surface corresponding to $\varPhi _{iso}=0.5$ acts in a traditional gradient-diffusive manner (Veynante et al. Reference Veynante, Trouvé, Bray and Mantel1997), acting to remove $\varSigma$ from the peak and diffuse it outwards. In fact, for a constant, non-dimensional turbulent diffusivity $\hat {D}_t=0.015$, it can be shown that the assumption

(6.9)\begin{equation} \widehat{\left\langle v\varSigma' \right\rangle}_s =-\hat{D}_t\,\frac{{\rm d}\hat{\varSigma}}{{\rm d}\xi} \end{equation}

gives an excellent match when $\varPhi _{iso}=0.5$, as shown in figure 9(a). For $\varPhi _{iso}=0.95$, where the iso-surface is located, on average, away from the centreline, the turbulent transport is still diffusive in nature by removing $\varSigma$ from the local peak. However, the diffusion is preferentially towards the centre of the mixing layer, rather than away from the centreline as might be expected. In this case, the assumption of a constant turbulent diffusivity is clearly incorrect, as demonstrated by the significant discrepancy between the two curves in figure 9(b). It is thought that the preferential diffusion towards the centreline is due to the fact that the turbulent fluctuations are greatest near $y/h=0$ (see e.g. figure 2a) and decay quickly to zero near the edge of the mixing layer. This could, perhaps, be accounted for in the turbulent diffusivity by choosing the standard form $D_t=\alpha u' \ell$, where $\alpha$ is a constant, $u'$ is the r.m.s. of the velocity fluctuations, and $\ell$ is a characteristic length (Pope Reference Pope2000), or by a two-equation model that better approximates the inhomogeneous nature of the turbulent fluctuations. Although this will not be investigated further in the present study, it should be emphasized that care should be taken in modelling the turbulent flux of an iso-surface, as the behaviour of $\mathcal {T}_t$ exhibits a strong dependence on the iso-value chosen in the present configuration.

Figure 9. Cross-stream profile of the surface weighted velocity $\left \langle v\varSigma ' \right \rangle$ in the self-similar period, compared to the gradient-diffusion hypothesis in (6.9), assuming constant turbulent diffusivity $\hat {D}_t=0.015$, for (a) $\varPhi _{iso}=0.5$ and (b) $\varPhi _{iso}=0.95$.

6.3. Production

Consider the term responsible for production of iso-surface area due to the fluid strain rate $\mathcal {P} = -\left \langle n_in_jS_{ij} \right \rangle _s\varSigma$. Self-similar scaling for this term can be deduced by considering that the correlation tangential strain rate of the scalar field, $\left \langle n_in_jS_{ij} \right \rangle _s$, has been shown to scale with the mean turbulent strain rate $(\varepsilon /\upsilon )^{1/2}$ (Poinsot & Veynante Reference Poinsot and Veynante2005; Kulkarni & Bisetti Reference Kulkarni and Bisetti2021). Based on the definition of the transverse Taylor length scale in (4.7), and noting that $u_{rms}\sim \Delta U$ in the present temporal mixing layer, it can be shown that $\lambda _g/\Delta U\sim (\varepsilon /\upsilon )^{-1/2}$. This implies that the tangential strain rate $\left \langle n_in_jS_{ij} \right \rangle _s$ scales approximately with $\lambda _g/\Delta U$. Recalling that $\varSigma \sim 1/\lambda _\phi$ and that $\lambda _g\sim \lambda _\phi$ in the present study, it is suggested that the production term scales according to

(6.10)\begin{equation} \mathcal{P} = \frac{\Delta U}{\lambda_\phi^2}\,\hat{\mathcal{P}}. \end{equation}

The self-similar profiles for $\mathcal {P}$ are displayed in figure 10. There is some discrepancy in the width of the profiles for this term, especially near $y/h=0$ for $\varPhi _{iso}=0.95$, although the difference is relatively small.

Figure 10. Proposed self-similar scaling of $\mathcal {P} = -\left \langle n_in_jS_{ij} \right \rangle _s\varSigma$ from (6.10), conditioned on (a) $\varPhi _{iso}=0.5$ and (b) $\varPhi _{iso}=0.95$, as functions of the similarity variable $\xi =y/h$. Solid and dashed lines are as in figure 6. Note that the magnitude of the peak value of $\mathcal {P}$ is significantly smaller near the edge of the mixing layer ($\varPhi _{iso}=0.95$) than it is near the centreline ($\varPhi _{iso}=0.5$).

The self-similar scaling provided here can be used to predict the behaviour of the integrated production term $\int \mathcal {P}$, discussed in figure 4. Based upon (6.10), the integrated production term is predicted to scale as $\int \mathcal {P}\sim \Delta U\,h/\lambda _\phi ^2$, which is independent of time (recall that $\lambda _\phi \sim h^{1/2}$). Qualitatively, this agrees with the observed behaviour of $\int \mathcal {P}$ from figure 4.

6.4. Diffusive transport

Before analysing the diffusive transport term $\mathcal {T}_D = -\partial (\langle w_{dif} n_i\rangle _s\varSigma )/\partial x_i$, it is helpful to first consider the self-similar behaviour of the surface-averaged diffusion velocity, i.e. $\left \langle w_{dif} n_i \varSigma ' \right \rangle = \left \langle w_{dif} n_i \right \rangle _s\varSigma$. To estimate the self-similar scaling of this term, a characteristic velocity scale for $w_{dif}$ is formed by considering the rate at which a scalar with diffusivity $D$ will diffuse over a length $\ell$, such that $w_{dif}\sim D/\ell$. It was determined empirically that choosing $\ell = \lambda _\phi$ results in the least error between instantaneous and self-similar profiles, which suggests that $\left \langle w_{dif} \right \rangle _s\varSigma \sim D/\lambda _\phi ^2$. Because $0\leq n_i\leq 1$, it is not expected that the normal vector will affect the self-similar scaling of this term (although it does affect the direction of propagation).

As shown in figure 11, the instantaneous profiles collapse onto the mean profile of the $y$ component of the surface-averaged diffusion velocity, $\left \langle w_{dif} n_y \right \rangle _s\varSigma$, for the proposed scaling. Note that only the $y$ component is shown here because it is the only component that contributes to $\mathcal {T}_D$.

Figure 11. Proposed self-similar scaling of $\langle w_{dif} n_y\rangle _s\varSigma$, conditioned on (a) $\varPhi _{iso}=0.5$ and (b) $\varPhi _{iso}=0.95$, as functions of the similarity variable $\xi =y/h$. Solid and dashed lines are as in figure 6.

The behaviour of $\left \langle w_{dif} n_y \right \rangle _s\varSigma$ in figure 11 is somewhat unintuitive. In figure 11(a), it is observed that the diffusion velocity of the $\varPhi _{iso}=0.5$ iso-surface is positive for $y/h<0$, and negative for $y/h>0$, which will cause $\varSigma$ to concentrate at $y/h=0$. Although it appears to be counterintuitive, this finding is consistent with the linear solution for a pure diffusion problem (i.e. where $U=0$). The value of the diffusion velocity for $\varPhi _{iso}=0.95$, shown in figure 11(b), is only positive, with a peak value located near the maximum of $\varSigma (\varPhi _{iso}=0.95)$. This suggests that, on average, the iso-surface associated with $\varPhi _{iso}=0.95$ will diffuse in the positive $y$ direction. This result is notably distinct from the behaviour observed for $\varPhi _{iso}=0.5$, but is nonetheless an expected result based on the solution to a purely diffusive problem with zero velocity.

To scale the diffusion term $\mathcal {T}_D=-\partial (\left \langle w_{dif} n_i \right \rangle _s\varSigma )/\partial x_i$ in (3.8), it is assumed that the derivative in the cross-stream direction introduces a factor $1/h$ to the scaling (similar to the argument for the advective flux $\mathcal {T}_U$ in § 6.2). Based on this assumption and the above scaling proposed for $\left \langle w_{dif} n_i \right \rangle _s\varSigma$, the self-similar form of $\mathcal {T}_D$ is given by

(6.11)\begin{equation} \mathcal{T}_D = \frac{D}{h\lambda_\phi^2}\,\hat{\mathcal{T}}_D. \end{equation}

The results for $\mathcal {T}_D$ using the above self-similar scaling are displayed in figure 12, demonstrating the collapse of instantaneous profiles onto a single self-similar profile for the proposed scaling above.

Figure 12. Proposed self-similar scaling of term $\mathcal {T}_D=-\partial (\left \langle w_{dif} n_i \right \rangle _s\varSigma )/\partial x_i$ from (6.11), conditioned on (a) $\varPhi _{iso}=0.5$ and (b) $\varPhi _{iso}=0.95$, as functions of the similarity variable $\xi =y/h$. Solid and dashed lines are as in figure 6.

Similar to the results for the diffusion velocity above, the behaviour of $\mathcal {T}_D$ is somewhat non-intuitive. Interestingly, for the $\varPhi _{iso}=0.5$ iso-surface shown in figure 12(a), $\mathcal {T}_D$ does not act to spread out or diffuse the profile of $\varSigma$, but rather acts to concentrate the profile $\varSigma$ at the location $y/h=0$. This finding is consistent with the behaviour of the diffusion velocity discussed previously. The behaviour of $\mathcal {T}_D$ for the iso-surface $\varPhi _{iso}=0.95$, shown in figure 12(b), is responsible for removing $\varSigma$ near the centre of the mixing layer, and transporting it to the outside of the mixing layer. This is consistent with the findings for the diffusion velocity and an intuitive understanding of the iso-surface behaviour.

For the present DNS, the magnitude of $\mathcal {T}_D$ is negligible compared to the other terms (see § 7); as such, the effect of molecular diffusion on $\partial \varSigma /\partial t$ is small and will not be investigated further. It should be noted that this term is not expected to be negligible for highly diffusive surfaces (i.e. $Sc\ll 1$), or active surfaces such as premixed flames, and will therefore require further study, especially given the non-intuitive behaviour observed herein.

6.5. Destruction

The self-similar development of $\mathcal {D} = -\left \langle w_{dif}\,\partial n_i/\partial x_i \right \rangle _s\varSigma$ can be understood by invoking a well-known identity that decomposes $w_{dif}$ into two terms, one related to diffusion in the direction normal to the iso-surface, $w_N$, and one related to the curvature of the iso-surface, $w_C$ (van Kalmthout & Veynante Reference van Kalmthout and Veynante1998):

(6.12)\begin{equation} w_{dif} =-\underbrace{\frac{D}{|\boldsymbol{\nabla}\varPhi|}\,\frac{\partial |\boldsymbol{\nabla}\varPhi|}{\partial x_i}\,n_i}_{w_N} -\underbrace{\frac{\partial n_i}{\partial x_i}}_{w_C}. \end{equation}

This decomposition can be used to split term $\mathcal {D}$ into two separate components,

(6.13)\begin{equation} \mathcal{D} = \underbrace{\left\langle w_N\,\frac{\partial n_i}{\partial x_i} \right\rangle_s\varSigma}_{\mathcal{D}_a} + \underbrace{D\left\langle \left(\frac{\partial n_i}{\partial x_i}\right)^2 \right\rangle_s\varSigma}_{\mathcal{D}_b}, \end{equation}

where $\mathcal {D}_b$ is notable because when substituted into (3.8), it must always take on a negative value in a manner analogous to the dissipation rates $\varepsilon$ and $\chi$. In contrast, $\mathcal {D}_a$ may take on either positive or negative values; in the present DNS, $\mathcal {D}_a$ acts predominantly to destroy iso-surface area density (except for a very slight region on the far outside of the mixing layer). Although some studies have suggested that $\mathcal {D}_a$ is negligible compared to $\mathcal {D}_b$ (van Kalmthout & Veynante Reference van Kalmthout and Veynante1998), the terms are found to be of comparable magnitude in the present study, as shown in figure 13. Because the two terms are of comparable magnitude over a wide range of iso-values, it is postulated that $\mathcal {D}_a$ and $\mathcal {D}_b$ will evolve together during the self-similar period. This assumption will be used to simplify the scaling argument below for the destruction term.

Figure 13. Decomposition of term $\mathcal {D}$ into components related to normal diffusion ($V_a$) and curvature ($V_b$) at $t\,\Delta U/h_0=462$, conditioned on (a) $\varPhi _{iso}=0.5$ and (b) $\varPhi _{iso}=0.95$. Terms are normalized by the mixing layer width at $t\,\Delta U/h=462$ and the velocity difference $h^2/\Delta U$. Note the difference in scales between (a) and (b).

As something of an aside, consider briefly the self-similar behaviour of the surface-averaged mean curvature $\left \langle \partial n_i/\partial x_i \right \rangle _s\varSigma$. The mean curvature is typically interpreted as the characteristic size of ‘wrinkles’ in the iso-surface. The appropriate scaling of this wrinkling length is somewhat controversial; previous studies have suggested that it scales with an integral scale of the flow (van Kalmthout & Veynante Reference van Kalmthout and Veynante1998), while others imply that it scales with the smallest features in the flow, i.e. the Kolmogorov scale $\eta$ (Kulkarni et al. Reference Kulkarni, Buttay, Kasbaoui, Attili and Bisetti2021). It has also been postulated that the mean curvature is proportional to the peak value of $\varSigma$ (Huh, Kwon & Lee Reference Huh, Kwon and Lee2013), although the derivation relies on the ‘generalized’ flame surface density (Boger et al. Reference Boger, Veynante, Boughanem and Trouvé1998) rather than the fine-grained iso-surface area density used here. Despite the differences, results from the current study are consistent with the analysis by Huh et al. (Reference Huh, Kwon and Lee2013), wherein the mean curvature is shown in figures 14(a,b) to evolve at the same rate as the peak value of $\varSigma$, i.e. $\left \langle \partial n_i/\partial x_i \right \rangle _s\sim \varSigma _{max}\sim 1/\lambda _\phi$. It can be seen that the proposed scaling results in a convincing collapse of the instantaneous profiles on the average over the self-similar period, for both of the iso-surfaces shown here.

Figure 14. Proposed self-similar scaling of $\langle \partial n_i/\partial x_i \rangle _s$ conditioned on (a) $\varPhi _{iso}=0.5$ and (b) $\varPhi _{iso}=0.95$, and $\langle (\partial n_i/\partial x_i)^2 \rangle _s$ conditioned on (c) $\varPhi _{iso}=0.5$ and (d) $\varPhi _{iso}=0.95$. Profiles are plotted as functions of the similarity variable $\xi =y/h$. Solid and dashed lines are as in figure 6. Note the difference in scales between the various curves.

One might expect that if the mean curvature scales like $1/\lambda _\phi$, then the mean square curvature would scale with $1/\lambda _\phi ^2$. However, according to the present DNS, the best collapse of the instantaneous profiles of $\left \langle (\partial n_i/\partial x_i)^2 \right \rangle _s$ occurs when scaled with $1/\eta ^2$. The instantaneous and self-similar profiles are displayed in figures 14(c,d) for $\varPhi _{iso}=0.5$ and $\varPhi _{iso}=0.95$, respectively, and demonstrate excellent agreement. From a physical standpoint, this can be understood by considering that the mean curvature is proportional to $\left \langle 1/r_1 + 2/r_2 \right \rangle _s$, where $r_1$ and $r_2$ are the radii of curvature of the iso-surface, and the mean square curvature is proportional to $\left \langle (1/r_1 + 1/r_2)^2 \right \rangle _s$. Clearly, the effect of the smallest length scales of the surface will dominate the mean square curvature, which is expected to be of the order of the Kolmogorov scale (Sreenivasan, Ramshankar & Meneveau Reference Sreenivasan, Ramshankar and Meneveau1989).

These results may be justified further by analogy to canonical scaling arguments involving velocity derivatives. For example, the mean velocity gradient in a shear layer is typically scaled by the mixing layer width $h$, i.e. $\left \langle \partial U_i/\partial x_j \right \rangle \sim \Delta U/h$, but the mean of the velocity gradient squared is scaled with the Taylor scale $\lambda$, i.e. $\left \langle (\partial U_i/\partial x_j)^2 \right \rangle \sim \Delta U^2/\lambda ^2$ (Tennekes & Lumley Reference Tennekes and Lumley1972). Therefore, it is not unreasonable to imagine that the mean curvature and mean square curvature scale separately from each other.

Returning now to the destruction term $\mathcal {D}$, based on the above discussion it is assumed that (1) $\mathcal {D}\sim \mathcal {D}_b$, and (2) $\left \langle (\partial n_i/\partial x_i)^2 \right \rangle _s\sim \eta ^{-2}$. This suggests the following self-similar scaling for the destruction,

(6.14)\begin{equation} \mathcal{D} = \frac{D}{\lambda_\phi\eta^2}\,\hat{\mathcal{D}}. \end{equation}

The instantaneous profiles are shown along with the self-similar average in figure 15, demonstrating the collapse of the profiles over the given self-similar period.

Figure 15. Proposed self-similar scaling of the destruction term $\mathcal {D}=\left \langle w_{dif}\,\partial n_i/\partial x_i \right \rangle _s\varSigma$ from (3.8), conditioned on (a) $\varPhi _{iso}=0.5$ and (b) $\varPhi _{iso}=0.95$, as functions of the similarity variable $\xi =y/h$. Solid and dashed lines are as in figure 6.

Now, it was demonstrated in figure 5 that the production and destruction terms are significantly larger than the remaining terms in (3.8), but of a similar magnitude to each other, suggesting that the production and destruction should scale similarly. However, from the current discussion, it is proposed that $\mathcal {D}\sim D/\lambda _\phi \eta ^2$, whereas $\mathcal {P}\sim \Delta U/\lambda _\phi ^2$. This discrepancy can be resolved by noting that in the present DNS with constant Schmidt number equal to $0.7$, the Kolmogorov and Batchelor scales are directly proportional, where the Batchelor scale is defined as $\eta _B = \eta \,Sc^{-1/2}$. From this definition, and the definition of the Kolmogorov scale in (2.2), it can be shown that

(6.15)\begin{equation} \eta_B^2 = D\left(\frac{\varepsilon}{\upsilon}\right)^{1/2}. \end{equation}

Noting that the Taylor scale, defined in (4.7), is proportional to $(\varepsilon /\upsilon )^{1/2}$, and that $\lambda _g\sim \lambda _\phi$ in the present DNS, it can be shown that

(6.16)\begin{equation} \eta^2\sim\eta_B^2\sim\frac{D\lambda_\phi}{\Delta U}. \end{equation}

Substituting this expression for $\eta ^2$ into the self-similar form given above for $\mathcal {D}$ yields

(6.17)\begin{equation} \mathcal{D}\sim\frac{\Delta U}{\lambda_\phi^2}\,\hat{\mathcal{D}}, \end{equation}

which is the same as the scaling observed for the production term. Note that although the Schmidt number dependence is included where possible, the present results assume a Schmidt number of $O(1)$ and may not be valid for flows with Schmidt numbers significantly different from unity, such as hydrogen diffusing in air or diluents such as salt in water. Furthermore, the diffusivity in the present simulations is constant and may not apply for flows with significant temperature or density gradients, such as premixed flames or highly stratified flows.

6.6. Net effect of production and destruction terms

The final term to analyse is the net effect of production and destruction, $K=\mathcal {P}-\mathcal {D}$. As discussed briefly in § 5.2, terms $\mathcal {P}$ and $\mathcal {D}$ are both an order of magnitude larger than $\partial \varSigma /\partial t$ and $\mathcal {T}_U$. Despite this discrepancy in magnitudes, it is clear that $\partial \varSigma /\partial t$ and $\mathcal {T}_U$ cannot be neglected. For example, the location of an iso-surface in the present mixing layer, say $\varPhi _{iso}>0.5$, must translate in the $+y$ direction for the mixing layer width to increase with time. Thus a non-trivial value of $\partial \varSigma /\partial t$ is required. As displayed in figure 5(b), computing the net effect of the production and destruction, $K$, yields a term that is of the same order of magnitude as $\partial \varSigma /\partial t$ and $\mathcal {T}_U$.

Assuming that $K$ will develop proportionally to $\partial \varSigma /\partial t$ and $\mathcal {T}_U$ yields the self-similar form

(6.18)\begin{equation} K = \frac{\Delta U}{h\lambda_\phi}\,\hat{K}. \end{equation}

The normalized cross-stream profiles are displayed in figure 16, which once again demonstrates agreement between the instantaneous and time-averaged profiles, aside from some fluctuations around $y/h=0$. Importantly, the fluctuations observed here are non-monotonic in time, i.e. the error is likely statistical in nature, not systematic. Notably, the scaling proposed here does not agree with the scaling proposed by Kulkarni & Bisetti (Reference Kulkarni and Bisetti2021), who suggest that $\mathcal {K}$ would scale in the same manner as $\mathcal {P}$ and $\mathcal {D}$.

Figure 16. Proposed self-similar scaling of $K$ from (6.18), conditioned on (a) $\varPhi _{iso}=0.5$ and (b) $\varPhi _{iso}=0.95$, as functions of the similarity variable $\xi =y/h$. Solid and dashed lines are as in figure 6.