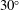1 Introduction
Given the relevance of laminar separation bubbles to applications such as unmanned aerial vehicles and turbomachine blades, a considerable number of studies have focused on the underlying stability and transition mechanisms. Marxen, Lang & Rist (Reference Marxen, Lang and Rist2012) note that amplification of disturbances is initiated in the laminar boundary layer, significantly upstream of the separation point. Prior to separation as well as in the laminar part of the laminar separation bubble (LSB), the mean flow is considered two-dimensional (Diwan & Ramesh Reference Diwan and Ramesh2012). Therefore, by assuming a low amplitude disturbance environment, linear stability theory (LST) may be applied successfully for determining unstable modes (Häggmark, Hildings & Henningson Reference Häggmark, Hildings and Henningson2001; Rist & Maucher Reference Rist and Maucher2002). The general consensus regarding the initial growth of these modes is that disturbances are convectively amplified via a Kelvin–Helmholtz instability mechanism (Ho & Huerre Reference Ho and Huerre1984; Watmuff Reference Watmuff1999; Diwan & Ramesh Reference Diwan and Ramesh2009). Amplification of disturbances through this mechanism leads to shear layer roll up and the formation of vortical structures in the aft portion of the LSB, manifesting as vortex shedding (Jones, Sandbergh & Sandham Reference Jones, Sandbergh and Sandham2008; Hain, Kähler & Radespiel Reference Hain, Kähler and Radespiel2009). It has been shown that, at a relatively low level of free-stream disturbances, although the initial shear layer roll up is strongly two-dimensional, spanwise deformation of the rollers quickly ensues in the vicinity of the reattachment region (Jones, Sandberg & Sandham Reference Jones, Sandberg and Sandham2010; Nati et al. Reference Nati, de Kat, Scarano and van Oudheusden2015; Kurelek, Lambert & Yarusevych Reference Kurelek, Lambert and Yarusevych2016; Kirk & Yarusevych Reference Kirk and Yarusevych2017).
Throughout the topical literature, several types of instabilities leading to three-dimensionality and spanwise roller deformations in laminar separation bubbles can be identified. Evidence of a Göertler type instability has been provided by Marxen et al. (Reference Marxen, Lang, Rist, Levin and Henningson2009), coupling streamline curvature at the beginning of the adverse pressure gradient with the formation of longitudinal vortices. Along these lines, highly localised instabilities of very small scale occur in cases of strong shear and have been related to the formation of hairpin vortices in transitional boundary layers (Bake, Meyer & Rist Reference Bake, Meyer and Rist2002). On the other hand, the spanwise deformation of rollers has been associated with a secondary absolute instability mechanism by several studies (e.g. Gaster Reference Gaster1992; Alam & Sandham Reference Alam and Sandham2000; Rist & Maucher Reference Rist and Maucher2002; Postl, Balzer & Fasel Reference Postl, Balzer and Fasel2011; Embacher & Fasel Reference Embacher and Fasel2014). The aforementioned studies propose that the interaction between the primary convective and the secondary absolute instabilities may create a global mechanism resulting in instantaneous spanwise deformations within the separated shear layer. Alam & Sandham (Reference Alam and Sandham2000) report that absolute instabilities may be prevalent when the reverse flow velocity magnitude in the LSB is between 15 and 20 % of the local free-stream velocity. In turn, Marxen, Lang & Rist (Reference Marxen, Lang and Rist2013) note that secondary instabilities can be either elliptic, causing spanwise deformation of vortex cores; or hyperbolic, active in the braid region between consecutive spanwise rollers. Although it is still debated whether the braid instability is of hyperbolic nature, evidence exists that multiple types of instabilities, either elliptic or hyperbolic, are simultaneously in action (Maucher, Rist & Wagner Reference Maucher, Rist and Wagner2000; Jones et al. Reference Jones, Sandbergh and Sandham2008; Marxen et al. Reference Marxen, Lang and Rist2013).
In addition, spanwise deformations have been related by several studies to a stationary global mode caused by a centrifugal instability (e.g. Theofilis, Hein & Dallmann Reference Theofilis, Hein and Dallmann2000; Theofilis, Barkley & Sherwin Reference Theofilis, Barkley and Sherwin2002; Rodríguez & Theofilis Reference Rodríguez and Theofilis2010). This mode is self-excited and has been shown to develop without the presence of external excitation in several cases where two-dimensional recirculation regions are encountered (e.g. Barkley, Gomes & Henderson Reference Barkley, Gomes and Henderson2002; Gallaire, Marquille & Ehrenstein Reference Gallaire, Marquille and Ehrenstein2007; Marquet et al.
Reference Marquet, Sipp, Chomaz and Jacquin2008; Passaggia, Leweke & Ehrenstein Reference Passaggia, Leweke and Ehrenstein2012). Rodríguez, Gennaro & Juniper (Reference Rodríguez, Gennaro and Juniper2013) demonstrate that the occurrence of such a global mode requires a minimum reverse flow magnitude within the separation bubble between 7 % and 8 % of the local free-stream velocity. Notwithstanding the role of global and/or absolute instabilities in the spanwise deformation of shedding structures, the common factor in the aforementioned studies is the relatively strong reverse flow, typically higher than 7 %. Nonetheless, LSBs featuring much milder reverse flows are common, such as the cases investigated by Rist & Maucher (Reference Rist and Maucher1994) (3 %), Spalart & Strelets (Reference Spalart and Strelets2000) (3 %), Alam & Sandham (Reference Alam and Sandham2000) (4 %), Rist & Augustin (Reference Rist and Augustin2006) (
![]() ${<}$
5 %), Marxen et al. (Reference Marxen, Lang and Rist2012) (
${<}$
5 %), Marxen et al. (Reference Marxen, Lang and Rist2012) (
![]() ${<}$
3 %), Yarusevych & Kotsonis (Reference Yarusevych and Kotsonis2017a
) (
${<}$
3 %), Yarusevych & Kotsonis (Reference Yarusevych and Kotsonis2017a
) (
![]() ${<}$
3 %) and Yarusevych & Kotsonis (Reference Yarusevych and Kotsonis2017b
) (
${<}$
3 %) and Yarusevych & Kotsonis (Reference Yarusevych and Kotsonis2017b
) (
![]() ${<}$
3 %). In these cases, the origin of spanwise deformations is currently unclear.
${<}$
3 %). In these cases, the origin of spanwise deformations is currently unclear.
Regardless of the instability mechanism responsible for the deformation and breakdown of dominant shear layer vortices in separation bubbles, disturbances in the laminar boundary layer upstream of the bubble must be considered, as these serve as an initial condition for the instabilities within an LSB (Diwan & Ramesh Reference Diwan and Ramesh2009). Linear stability analysis carried out by Mack (Reference Mack1984) on a flat plate boundary layer at Reynolds numbers based on streamwise distance from the leading edge below 1800, indicates that oblique disturbances may be more unstable than normal Tollmien–Schlichting (TS) waves for certain wavenumber vector angles. Indeed, the interaction between normal and oblique modes is responsible for the three-dimensional flow evolutions in K-type (Klebanoff, Tidstrom & Sargent Reference Klebanoff, Tidstrom and Sargent1962), H-type (Herbert Reference Herbert1988) and oblique (King & Breuer Reference King and Breuer2002) transition. A model of such an interaction scenario has been proposed by Craik (Reference Craik1971) and extended by Zelman & Maslennikova (Reference Zelman and Maslennikova1993). It considers the formation of a symmetric resonant triad between a two-dimensional TS wave and two oblique TS waves propagating at equal but opposite angles with respect to the flow. Notably, the streamwise wavenumber of the oblique pair is half of the TS streamwise wavenumber, thus, the interaction is often referred to as subharmonic. A resonance condition occurs when phase velocities of the aforementioned waves match. The emergence of subharmonic resonant waves has been demonstrated by several experimental studies (e.g. Kachanov & Levchenko Reference Kachanov and Levchenko1984; Corke & Mangano Reference Corke and Mangano1989). Although the aforementioned studies consider only attached flows, they provide valuable insight for the present investigation, as the state of the boundary layer upstream of separation directly affects the dynamics of a laminar separation bubble.
Rist & Augustin (Reference Rist and Augustin2006) and Marxen et al. (Reference Marxen, Lang and Rist2013) have demonstrated through direct numerical simulations of a flat plate laminar separation bubble that introducing oblique disturbances at moderate angles in the boundary layer upstream of separation causes spanwise staggering of the roll-up process. In the time-averaged sense, this results in a peak–valley distribution of the LSB dividing streamline. In addition, measurements performed by Burgmann, Brücker & Schröder (Reference Burgmann, Brücker and Schröder2006), Burgmann, Dannemann & Schröder (Reference Burgmann, Dannemann and Schröder2008), Burgmann & Schröder (Reference Burgmann and Schröder2008) and Wolf et al. (Reference Wolf, Kähler, Trooling, Kykal and Lai2011) on a laminar separation bubble developing on an aerofoil at higher free-stream turbulence levels, demonstrate the occurrence of a group of C-shaped vortices in the vicinity of the reattachment region. These vortices are found to have a staggered arrangement that persists in the wake of the aerofoil; however, the mechanism responsible for the formation of these patterns remains unexplained.
In order to determine the active instabilities in the LSB, the incoming boundary layer is often forced with periodic perturbations. These are introduced in a two-dimensional fashion through wall oscillators (Alam & Sandham Reference Alam and Sandham2000; Marxen et al. Reference Marxen, Lang, Rist, Levin and Henningson2009), acoustic excitation (Yarusevych, Sullivan & Kawall Reference Yarusevych, Sullivan and Kawall2007; Jones et al. Reference Jones, Sandberg and Sandham2010) and plasma actuators (Yarusevych & Kotsonis Reference Yarusevych and Kotsonis2017a ). The aforementioned periodic type of forcing is continuous at a frequency equal to the fundamental frequency of the unstable boundary layer or LSB shedding. An alternative forcing scheme, first suggested by Gaster & Grant (Reference Gaster and Grant1975), employs an impulsive disturbance that excites all instability modes, thus, generating a wave packet through selective amplification. However, when introduced as a point source, e.g. through a pressure tap, strong nonlinear effects can be observed in the wave packet (Cohen, Breuer & Haritonidis Reference Cohen, Breuer and Haritonidis1991; Medeiros & Gaster Reference Medeiros and Gaster1999).
The present study is an investigation of the three-dimensional deformations of coherent structures in a laminar separation bubble of low reverse flow magnitude (
![]() ${\approx}$
2 %) and assessment of a possible link of the observed phenomena with the stability characteristics of the incoming boundary layer. An LSB is formed on a flat plate subjected to an adverse pressure gradient, that captures the fundamental characteristics of LSBs observed on aerofoil sections (Gaster Reference Gaster1967; Gaster & Grant Reference Gaster and Grant1975). To excite the primary instability mode, the flow is impulsively forced. In line with Michelis, Kotsonis & Yarusevych (Reference Michelis, Kotsonis and Yarusevych2017), forcing is applied in a two-dimensional fashion by means of a spanwise-uniform dielectric-barrier-discharge (DBD) plasma actuator (Corke, Enloe & Wilkinson Reference Corke, Enloe and Wilkinson2010; Kotsonis Reference Kotsonis2015), located upstream of the separation point, thus circumventing the shortcomings of localised point forcing discussed earlier. In addition, an essential feature of impulsive forcing is that, for fixed free-stream velocity and turbulent intensity, the bubble experiences elevated disturbance levels only during the forcing impulse, otherwise being subjected to natural level of disturbances. Consequently, in contrast to continuous forcing, the flow evolution following the wave packet convection occurs without further conditioning the incoming disturbances.
${\approx}$
2 %) and assessment of a possible link of the observed phenomena with the stability characteristics of the incoming boundary layer. An LSB is formed on a flat plate subjected to an adverse pressure gradient, that captures the fundamental characteristics of LSBs observed on aerofoil sections (Gaster Reference Gaster1967; Gaster & Grant Reference Gaster and Grant1975). To excite the primary instability mode, the flow is impulsively forced. In line with Michelis, Kotsonis & Yarusevych (Reference Michelis, Kotsonis and Yarusevych2017), forcing is applied in a two-dimensional fashion by means of a spanwise-uniform dielectric-barrier-discharge (DBD) plasma actuator (Corke, Enloe & Wilkinson Reference Corke, Enloe and Wilkinson2010; Kotsonis Reference Kotsonis2015), located upstream of the separation point, thus circumventing the shortcomings of localised point forcing discussed earlier. In addition, an essential feature of impulsive forcing is that, for fixed free-stream velocity and turbulent intensity, the bubble experiences elevated disturbance levels only during the forcing impulse, otherwise being subjected to natural level of disturbances. Consequently, in contrast to continuous forcing, the flow evolution following the wave packet convection occurs without further conditioning the incoming disturbances.
The spatio-temporal flow development is characterised via time-resolved particle image velocimetry (PIV). Two-component planar PIV is used to capture the streamwise characteristics of the LSB, while tomographic PIV is employed for investigating the full three-dimensional velocity field in the roll-up region of the LSB. Upstream of the PIV field of view, the flow is assessed by means of numerical solution of the boundary layer equations, based on the measured pressure distribution. The combined numerical solution and experimentally measured mean flow forms the base for linear stability theory (LST) analysis. The performed analysis explores the link between the boundary layer stability characteristics and the ensuing development of coherent structures in the separated shear layer, and provides a handle for future control strategies.
2 Experimental apparatus and techniques
2.1 Notation
The following notation conventions are applied. Dimensional quantities are noted by a tilde and, where appropriate, accompanied by their respective unit (e.g.
![]() $\tilde{x}~(\text{mm})$
). Scaling is performed using quantities of the baseline unforced laminar separation bubble. In particular, lengths are scaled with the displacement thickness at separation,
$\tilde{x}~(\text{mm})$
). Scaling is performed using quantities of the baseline unforced laminar separation bubble. In particular, lengths are scaled with the displacement thickness at separation,
![]() $\tilde{\unicode[STIX]{x1D6FF}}_{s_{0}}^{\ast }=2.39~\text{mm}$
, while velocities with the respective local free-stream velocity at separation,
$\tilde{\unicode[STIX]{x1D6FF}}_{s_{0}}^{\ast }=2.39~\text{mm}$
, while velocities with the respective local free-stream velocity at separation,
![]() $\tilde{U} _{\infty _{s}}=8.6~\text{m}~\text{s}^{-1}$
. Non-dimensional quantities are noted by their respective symbol (e.g.
$\tilde{U} _{\infty _{s}}=8.6~\text{m}~\text{s}^{-1}$
. Non-dimensional quantities are noted by their respective symbol (e.g.
![]() $x=\tilde{x}/\tilde{\unicode[STIX]{x1D6FF}}_{s_{0}}^{\ast }$
,
$x=\tilde{x}/\tilde{\unicode[STIX]{x1D6FF}}_{s_{0}}^{\ast }$
,
![]() $u=\tilde{u} /\tilde{U} _{\infty _{s}}$
). The aforementioned scaling factors are also used to determine the Reynolds number pertinent to this experiment,
$u=\tilde{u} /\tilde{U} _{\infty _{s}}$
). The aforementioned scaling factors are also used to determine the Reynolds number pertinent to this experiment,
![]() $Re_{\unicode[STIX]{x1D6FF}_{s}^{\ast }}=\tilde{U} _{\infty _{s}}\tilde{\unicode[STIX]{x1D6FF}}_{s_{0}}^{\ast }/\tilde{\unicode[STIX]{x1D708}}=1305$
. Moreover, they are combined for obtaining non-dimensional frequencies through the definition of the Strouhal number,
$Re_{\unicode[STIX]{x1D6FF}_{s}^{\ast }}=\tilde{U} _{\infty _{s}}\tilde{\unicode[STIX]{x1D6FF}}_{s_{0}}^{\ast }/\tilde{\unicode[STIX]{x1D708}}=1305$
. Moreover, they are combined for obtaining non-dimensional frequencies through the definition of the Strouhal number,
![]() $St=\tilde{f}\tilde{\unicode[STIX]{x1D6FF}}_{s_{0}}^{\ast }/\tilde{U} _{\infty _{s}}$
. Quantities derived from time averaging are identified with an overline (e.g.
$St=\tilde{f}\tilde{\unicode[STIX]{x1D6FF}}_{s_{0}}^{\ast }/\tilde{U} _{\infty _{s}}$
. Quantities derived from time averaging are identified with an overline (e.g.
![]() $\bar{u}$
) while their fluctuating component by a dash (e.g.
$\bar{u}$
) while their fluctuating component by a dash (e.g.
![]() $u^{\prime }$
). The notation
$u^{\prime }$
). The notation
![]() $(h,k)$
is used to denote instability modes, where
$(h,k)$
is used to denote instability modes, where
![]() $h$
and
$h$
and
![]() $k$
are integer multiples of the fundamental frequency
$k$
are integer multiples of the fundamental frequency
![]() $(\tilde{f}_{0})$
and spanwise wavenumber
$(\tilde{f}_{0})$
and spanwise wavenumber
![]() $(\unicode[STIX]{x1D6FD}_{r_{0}})$
, respectively (see § 3.2). Finally, time is normalised by the fundamental shedding frequency, yielding
$(\unicode[STIX]{x1D6FD}_{r_{0}})$
, respectively (see § 3.2). Finally, time is normalised by the fundamental shedding frequency, yielding
![]() $\unicode[STIX]{x1D70F}=\tilde{t}\tilde{f}_{0}$
.
$\unicode[STIX]{x1D70F}=\tilde{t}\tilde{f}_{0}$
.
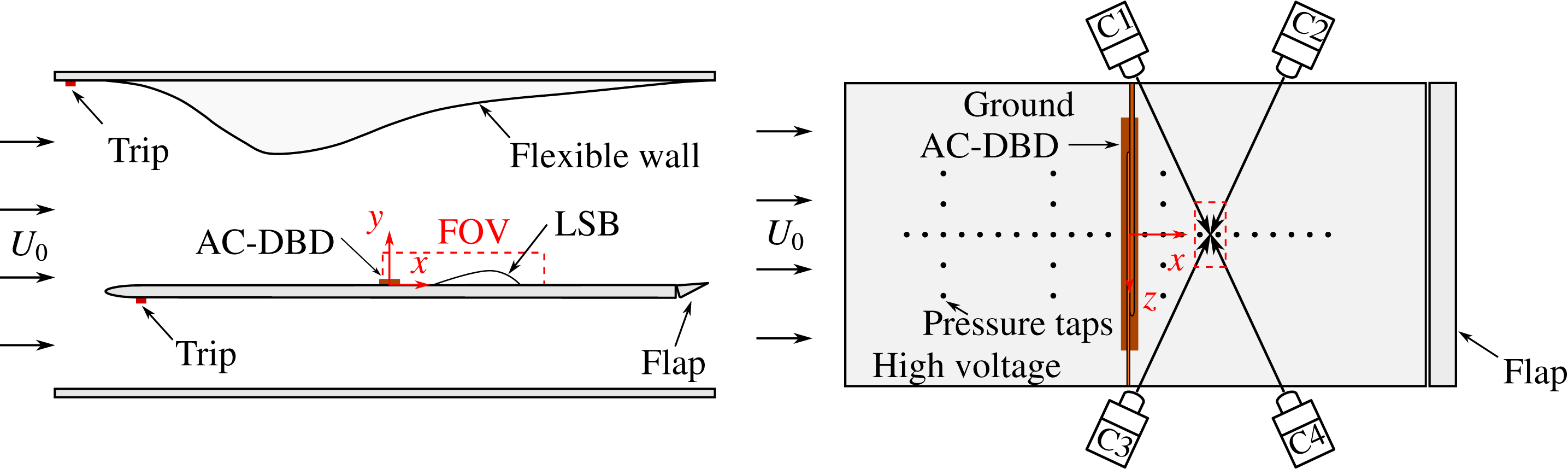
Figure 1. Overview of the experimental set-up. The four camera arrangement shown corresponds to the tomographic configuration.
2.2 Set-up overview
The experimental set-up used for this study (figure 1) is identical to the one described in Michelis et al. (Reference Michelis, Kotsonis and Yarusevych2017). The flat plate is 1000 mm long, 500 mm wide and 20 mm thick, while its leading edge is a modified super ellipse (Lin, Reed & Saric Reference Lin, Reed and Saric1992). The pressure gradient on the flat plate is conditioned by a flexible polycarbonate body. Zig-zag turbulators are employed to trip the lower side of the flat plate and the incoming boundary layer of the flexible wall in order to mitigate unsteady boundary layer fluctuations and separation, respectively. Tuft flow visualisation and PIV measurements were used to confirm suppression of the aforementioned effects. A Cartesian coordinate system is defined such that
![]() $\tilde{x}=0$
lies 420 mm from the flat plate leading edge,
$\tilde{x}=0$
lies 420 mm from the flat plate leading edge,
![]() ${\tilde{y}}=0$
at its top surface and
${\tilde{y}}=0$
at its top surface and
![]() $\tilde{z}=0$
at its midspan. The free-stream velocity
$\tilde{z}=0$
at its midspan. The free-stream velocity
![]() $(\tilde{U} _{0})$
is set at
$(\tilde{U} _{0})$
is set at
![]() $6.4~\text{m}~\text{s}^{-1}$
, for which the turbulence intensity (
$6.4~\text{m}~\text{s}^{-1}$
, for which the turbulence intensity (
![]() $\text{TI}=\tilde{U} _{rms}^{\prime }/\tilde{U} _{0}$
, where
$\text{TI}=\tilde{U} _{rms}^{\prime }/\tilde{U} _{0}$
, where
![]() $\tilde{U} _{rms}^{\prime }$
is the root mean square of the velocity fluctuations) is below 0.2 % between 0.1 and 1 kHz. The imposed pressure gradient is expressed in terms of surface pressure coefficient,
$\tilde{U} _{rms}^{\prime }$
is the root mean square of the velocity fluctuations) is below 0.2 % between 0.1 and 1 kHz. The imposed pressure gradient is expressed in terms of surface pressure coefficient,
![]() $C_{p}$
(figure 2). It can be seen from the distinct topology of surface pressure distribution in figure 2 that a laminar separation bubble develops with separation and reattachment locations at
$C_{p}$
(figure 2). It can be seen from the distinct topology of surface pressure distribution in figure 2 that a laminar separation bubble develops with separation and reattachment locations at
![]() $\tilde{x}_{s}\approx 30~\text{mm}$
and
$\tilde{x}_{s}\approx 30~\text{mm}$
and
![]() $\tilde{x}_{r}\approx 180~\text{mm}$
, respectively.
$\tilde{x}_{r}\approx 180~\text{mm}$
, respectively.
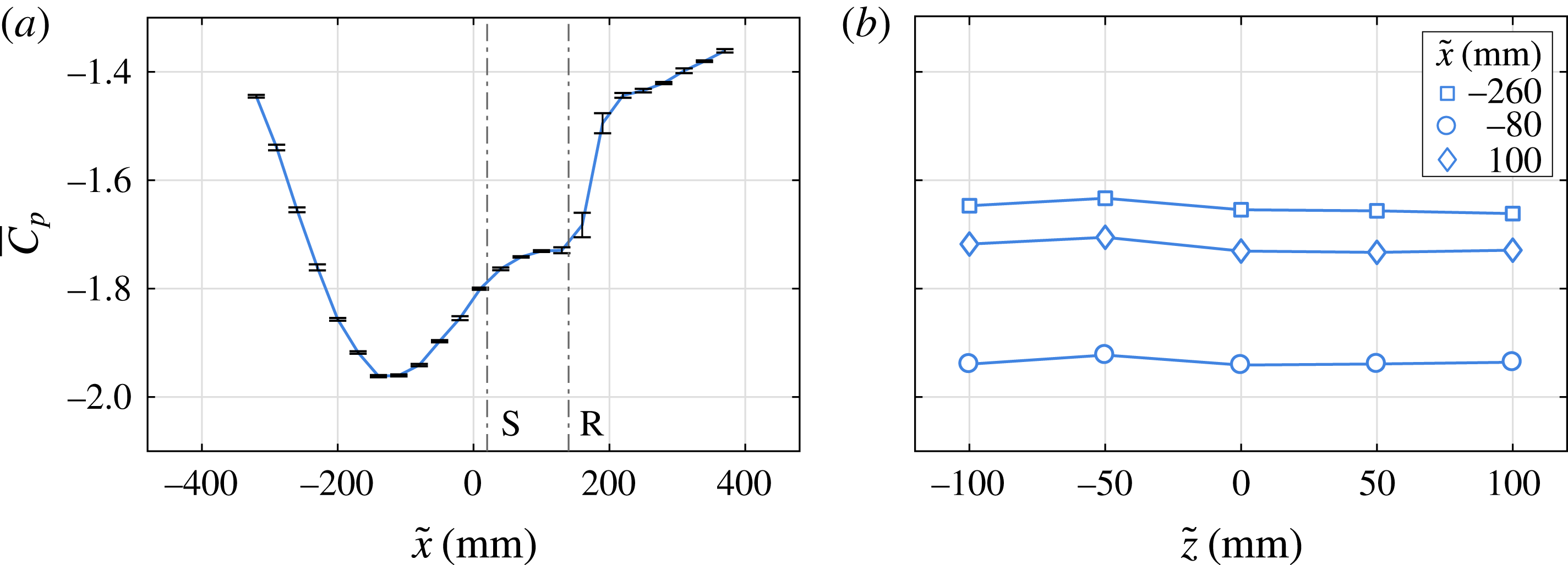
Figure 2.
![]() $C_{p}$
distribution in (a) streamwise and (b) spanwise directions. S and R mark the time-averaged separation and reattachment points, respectively, estimated from planar PIV.
$C_{p}$
distribution in (a) streamwise and (b) spanwise directions. S and R mark the time-averaged separation and reattachment points, respectively, estimated from planar PIV.
2.3 Impulsive forcing
An alternating current, dielectric-barrier-discharge (AC-DBD) plasma actuator (Corke et al.
Reference Corke, Enloe and Wilkinson2010; Benard & Moreau Reference Benard and Moreau2014; Kotsonis Reference Kotsonis2015; Michelis & Kotsonis Reference Michelis and Kotsonis2015) is employed for introducing a two-dimensional controlled disturbance upstream of the LSB mean separation point. The complete actuator thickness (electrodes and dielectric) is less than
![]() $70~\unicode[STIX]{x03BC}\text{m}$
; significantly thinner than the local boundary layer thickness
$70~\unicode[STIX]{x03BC}\text{m}$
; significantly thinner than the local boundary layer thickness
![]() $({\approx}5.5~\text{mm})$
. The discharge gap, located at a distance of 420 mm from the leading edge in the streamwise direction, serves as the origin of the reference system (figure 1). The forcing signal is constructed by modulating a sinusoidal signal
$({\approx}5.5~\text{mm})$
. The discharge gap, located at a distance of 420 mm from the leading edge in the streamwise direction, serves as the origin of the reference system (figure 1). The forcing signal is constructed by modulating a sinusoidal signal
![]() $(\tilde{f}_{c}=5~\text{kHz})$
with a square signal and the duty cycle is selected such that a 1 ms pulse is produced. Under the experimental conditions described here, the frequencies associated with the LSB vortex shedding and flapping are of the order of 130 and 10 Hz respectively (Michelis et al.
Reference Michelis, Kotsonis and Yarusevych2017). Since the carrier frequency
$(\tilde{f}_{c}=5~\text{kHz})$
with a square signal and the duty cycle is selected such that a 1 ms pulse is produced. Under the experimental conditions described here, the frequencies associated with the LSB vortex shedding and flapping are of the order of 130 and 10 Hz respectively (Michelis et al.
Reference Michelis, Kotsonis and Yarusevych2017). Since the carrier frequency
![]() $(\tilde{f}_{c}=5~\text{kHz})$
exceeds the relevant hydrodynamic frequencies by approximately two orders of magnitude, a pulse is equivalent to a single impulsive perturbation. The moment of actuation is selected as reference time
$(\tilde{f}_{c}=5~\text{kHz})$
exceeds the relevant hydrodynamic frequencies by approximately two orders of magnitude, a pulse is equivalent to a single impulsive perturbation. The moment of actuation is selected as reference time
![]() $\tilde{t}_{0}=0~\text{s}$
.
$\tilde{t}_{0}=0~\text{s}$
.
In quiescent conditions, continuous operation of the actuator at voltage amplitude of 5 kV and carrier frequency of 5 kHz results in a downstream jet velocity of the order of
![]() $1~\text{m}~\text{s}^{-1}$
. The force exerted on the fluid is expressed in terms of momentum coefficient,
$1~\text{m}~\text{s}^{-1}$
. The force exerted on the fluid is expressed in terms of momentum coefficient,
![]() $C_{\unicode[STIX]{x1D707}}$
(Amitay et al.
Reference Amitay, Smith, Kibens, Parekh and Glezer2001), and is estimated through application of the momentum balance equation on PIV-measured velocity fields within the appropriate control volume (Kotsonis et al.
Reference Kotsonis, Ghaemi, Veldhuis and Scarano2011). The majority of the momentum exchange occurs along the streamwise direction, for which
$C_{\unicode[STIX]{x1D707}}$
(Amitay et al.
Reference Amitay, Smith, Kibens, Parekh and Glezer2001), and is estimated through application of the momentum balance equation on PIV-measured velocity fields within the appropriate control volume (Kotsonis et al.
Reference Kotsonis, Ghaemi, Veldhuis and Scarano2011). The majority of the momentum exchange occurs along the streamwise direction, for which
![]() $C_{\unicode[STIX]{x1D707}}$
is calculated to be
$C_{\unicode[STIX]{x1D707}}$
is calculated to be
![]() $1.6\times 10^{-4}$
. Due to the imposed free-stream velocity being relatively weak, the jet topology and the value of
$1.6\times 10^{-4}$
. Due to the imposed free-stream velocity being relatively weak, the jet topology and the value of
![]() $C_{\unicode[STIX]{x1D707}}$
are not significantly affected with respect to the quiescent conditions (Pereira, Ragni & Kotsonis Reference Pereira, Ragni and Kotsonis2014).
$C_{\unicode[STIX]{x1D707}}$
are not significantly affected with respect to the quiescent conditions (Pereira, Ragni & Kotsonis Reference Pereira, Ragni and Kotsonis2014).
2.4 Particle image velocimetry
The flow field is investigated with two different time-resolved PIV configurations, planar and tomographic (Elsinga et al.
Reference Elsinga, Scarano, Wieneke and van Oudheusden2006). Planar PIV is used for determining the overall bubble features and dynamics on the
![]() $x$
–
$x$
–
![]() $y$
plane. In contrast, tomographic PIV focuses on the reattachment region of the bubble, where three-dimensional flow characteristics are examined.
$y$
plane. In contrast, tomographic PIV focuses on the reattachment region of the bubble, where three-dimensional flow characteristics are examined.
In the planar configuration, in order to obtain statistical information as well as for resolving the relevant phenomena, image pairs
![]() $(\unicode[STIX]{x0394}\tilde{t}=60~\unicode[STIX]{x03BC}\text{s})$
are recorded at acquisition frequencies
$(\unicode[STIX]{x0394}\tilde{t}=60~\unicode[STIX]{x03BC}\text{s})$
are recorded at acquisition frequencies
![]() $(\tilde{f}_{a})$
of 250, 500 and 2000 Hz. For each acquisition frequency, 10 914 cropped image pairs are recorded, thus, the acquisition times are 43.7, 21.8 and 5.5 s respectively. Particle displacements are calculated by applying the multi-step interrogation window algorithm (Scarano & Riethmuller Reference Scarano and Riethmuller2000) from an initial window of
$(\tilde{f}_{a})$
of 250, 500 and 2000 Hz. For each acquisition frequency, 10 914 cropped image pairs are recorded, thus, the acquisition times are 43.7, 21.8 and 5.5 s respectively. Particle displacements are calculated by applying the multi-step interrogation window algorithm (Scarano & Riethmuller Reference Scarano and Riethmuller2000) from an initial window of
![]() $48\times 48$
pixels to a final window of
$48\times 48$
pixels to a final window of
![]() $12\times 12$
pixels, with 75 % overlap between windows. This results in a vector spacing of 0.19 mm in both streamwise and wall-normal directions. The vector fields from the two cameras overlap by approximately 10 % and are stitched to obtain a combined field of 131 by 14 mm.
$12\times 12$
pixels, with 75 % overlap between windows. This results in a vector spacing of 0.19 mm in both streamwise and wall-normal directions. The vector fields from the two cameras overlap by approximately 10 % and are stitched to obtain a combined field of 131 by 14 mm.
For the tomographic configuration, four cameras are used, placed in a rectangular arrangement above the flat plate, at an inclination of approximately
![]() $20^{\circ }$
with respect to the wall-normal axis. In order to adjust the focal plane alignment on the camera sensor, objectives are mounted on the cameras via Scheimpflug adapters. The volume of interest is illuminated using the multi-pass light amplification technique (Ghaemi & Scarano Reference Ghaemi and Scarano2010). Volume calibration is performed with the self-calibration technique (Wieneke Reference Wieneke2008), for which residual disparity of less than 0.1 pixels is achieved. Image pairs
$20^{\circ }$
with respect to the wall-normal axis. In order to adjust the focal plane alignment on the camera sensor, objectives are mounted on the cameras via Scheimpflug adapters. The volume of interest is illuminated using the multi-pass light amplification technique (Ghaemi & Scarano Reference Ghaemi and Scarano2010). Volume calibration is performed with the self-calibration technique (Wieneke Reference Wieneke2008), for which residual disparity of less than 0.1 pixels is achieved. Image pairs
![]() $(\unicode[STIX]{x0394}\tilde{t}=140~\unicode[STIX]{x03BC}\text{s})$
are recorded at acquisition frequencies of
$(\unicode[STIX]{x0394}\tilde{t}=140~\unicode[STIX]{x03BC}\text{s})$
are recorded at acquisition frequencies of
![]() $\tilde{f}_{a}=125$
and 2000 Hz. The acquisition time over 6236 cropped image pairs is, therefore, 49.9 and 3.1 s for each acquisition frequency respectively. The volume reconstruction from the acquired images is obtained by executing the simultaneous implementation of multiplicative algebraic reconstruction techniques (SMART) operation (Atkinson & Soria Reference Atkinson and Soria2009), yielding a total interrogation volume of
$\tilde{f}_{a}=125$
and 2000 Hz. The acquisition time over 6236 cropped image pairs is, therefore, 49.9 and 3.1 s for each acquisition frequency respectively. The volume reconstruction from the acquired images is obtained by executing the simultaneous implementation of multiplicative algebraic reconstruction techniques (SMART) operation (Atkinson & Soria Reference Atkinson and Soria2009), yielding a total interrogation volume of
![]() $448\times 827\times 66$
voxels. Particle displacement calculation in the interrogation volume is performed in multiple window steps, from an initial of
$448\times 827\times 66$
voxels. Particle displacement calculation in the interrogation volume is performed in multiple window steps, from an initial of
![]() $72\times 72\times 20$
voxels to a final of
$72\times 72\times 20$
voxels to a final of
![]() $48\times 48\times 11$
voxels, with 75 % overlap. This results in a vector volume of
$48\times 48\times 11$
voxels, with 75 % overlap. This results in a vector volume of
![]() $36\times 68\times 31$
vectors
$36\times 68\times 31$
vectors
![]() $(49.9\times 95.6\times 7.1~\text{mm}^{3})$
along the
$(49.9\times 95.6\times 7.1~\text{mm}^{3})$
along the
![]() $x$
,
$x$
,
![]() $z$
and
$z$
and
![]() $y$
directions, respectively. The corresponding vector pitch in the three directions is 1.42, 1.42 and 0.24 mm.
$y$
directions, respectively. The corresponding vector pitch in the three directions is 1.42, 1.42 and 0.24 mm.

Figure 3. Planar PIV time-averaged (a) streamwise velocity and (b) spanwise vorticity. Solid line: dividing streamline. Dashed line: displacement thickness. Dash-dotted line: region where the reverse flow magnitude is 1 %–2 % of the local free-stream velocity
![]() $(\bar{u}_{\infty })$
, the contour line itself indicating 1 %.
$(\bar{u}_{\infty })$
, the contour line itself indicating 1 %.
![]() $\circ$
: maximum height. S and R mark separation and reattachment, respectively.
$\circ$
: maximum height. S and R mark separation and reattachment, respectively.
For both configurations, estimation of the instantaneous uncertainty is determined through the linear error propagation technique (Sciacchitano & Wieneke Reference Sciacchitano and Wieneke2016). The maximum uncertainty on the planar configuration average field is
![]() $\unicode[STIX]{x1D700}_{u}\approx 0.2\,\%$
and
$\unicode[STIX]{x1D700}_{u}\approx 0.2\,\%$
and
![]() $\unicode[STIX]{x1D700}_{v}\approx 0.7\,\%$
. Uncertainty for the tomographic configuration is higher, with values of
$\unicode[STIX]{x1D700}_{v}\approx 0.7\,\%$
. Uncertainty for the tomographic configuration is higher, with values of
![]() $\unicode[STIX]{x1D700}_{u}\approx 1\,\%$
,
$\unicode[STIX]{x1D700}_{u}\approx 1\,\%$
,
![]() $\unicode[STIX]{x1D700}_{v}\approx 5\,\%$
and
$\unicode[STIX]{x1D700}_{v}\approx 5\,\%$
and
![]() $\unicode[STIX]{x1D700}_{w}\approx 5\,\%$
.
$\unicode[STIX]{x1D700}_{w}\approx 5\,\%$
.
3 Baseline LSB
3.1 Steady state features
Time-averaged velocity fields from planar and tomographic PIV configurations are shown in figures 3 and 4. A closed recirculation region forms in the time-averaged sense as the boundary layer separates and reattaches. The mean dividing streamline is estimated on the planar data and outlines the separation bubble (figure 3). Based on this streamline, the mean separation and reattachment points are estimated at
![]() $\bar{x}_{s}=6.3$
and
$\bar{x}_{s}=6.3$
and
![]() $\bar{x}_{r}=47.5$
respectively, therefore, the length of the LSB is
$\bar{x}_{r}=47.5$
respectively, therefore, the length of the LSB is
![]() $\bar{l}_{b}=41.2$
. The bubble height is defined by the maximum wall-normal distance of the dividing streamline from the wall. This is evaluated to be
$\bar{l}_{b}=41.2$
. The bubble height is defined by the maximum wall-normal distance of the dividing streamline from the wall. This is evaluated to be
![]() $\bar{h}=0.73$
, occurring at
$\bar{h}=0.73$
, occurring at
![]() $\bar{x}_{h}=41.7$
. The maximum amplitude of the reverse flow encountered within the LSB is of the order of 2 % of the local free-stream velocity, comparable to Rist & Maucher (Reference Rist and Maucher1994) (3 %), Spalart & Strelets (Reference Spalart and Strelets2000) (3 %) as well as Marxen et al. (Reference Marxen, Lang and Rist2012)
$\bar{x}_{h}=41.7$
. The maximum amplitude of the reverse flow encountered within the LSB is of the order of 2 % of the local free-stream velocity, comparable to Rist & Maucher (Reference Rist and Maucher1994) (3 %), Spalart & Strelets (Reference Spalart and Strelets2000) (3 %) as well as Marxen et al. (Reference Marxen, Lang and Rist2012)
![]() $({<}3\,\%)$
. In addition, the pressure gradient parameter formulated by Gaster (Reference Gaster1967) is
$({<}3\,\%)$
. In addition, the pressure gradient parameter formulated by Gaster (Reference Gaster1967) is
![]() $P\simeq -0.11$
for a corresponding Reynolds number based on momentum thickness at separation of
$P\simeq -0.11$
for a corresponding Reynolds number based on momentum thickness at separation of
![]() $Re_{\unicode[STIX]{x1D703}_{s}}=345$
. The above classify the current separation bubble as short, hence, as suggested by previous studies (Gaster Reference Gaster1992; Alam & Sandham Reference Alam and Sandham2000; Rist & Maucher Reference Rist and Maucher2002), convective instabilities are expected to dominate in the separated shear layer.
$Re_{\unicode[STIX]{x1D703}_{s}}=345$
. The above classify the current separation bubble as short, hence, as suggested by previous studies (Gaster Reference Gaster1992; Alam & Sandham Reference Alam and Sandham2000; Rist & Maucher Reference Rist and Maucher2002), convective instabilities are expected to dominate in the separated shear layer.

Figure 4. (a) Planar PIV time-averaged streamwise velocity profiles. Solid line: dividing streamline. Dashed line: displacement thickness.
![]() ${\vartriangle}$
: separation point,
${\vartriangle}$
: separation point,
![]() $\triangledown$
: reattachment point,
$\triangledown$
: reattachment point,
![]() $\circ$
: maximum height. The box indicates the tomographic PIV measurement volume projection. (b) Tomographic PIV time-averaged velocity field. The iso-surface marks the bubble outline. Slices depict wall-normal velocity. (c) Fluctuation of spanwise velocity component,
$\circ$
: maximum height. The box indicates the tomographic PIV measurement volume projection. (b) Tomographic PIV time-averaged velocity field. The iso-surface marks the bubble outline. Slices depict wall-normal velocity. (c) Fluctuation of spanwise velocity component,
![]() $\unicode[STIX]{x1D70E}_{w}$
, at
$\unicode[STIX]{x1D70E}_{w}$
, at
![]() $x=50$
.
$x=50$
.
The volume captured by the tomographic configuration with respect to the separation bubble is indicated by a grey rectangle in figure 4(a). Due to experimental limitations, no tomographic data have been acquired below
![]() $y=0.39$
. Figure 4(b) depicts a three-dimensional outline of the separation bubble as well as several slices of wall-normal velocity. The results show minimal spanwise variation in the dividing streamline within the fore portion of the bubble, confirming the two-dimensional nature of the time-averaged incoming flow. In contrast, the time-averaged topology in the reattachment region shows distinct spanwise non-uniformities manifested by spatially periodic peaks and valleys, with a similar trend persisting in the fluctuation of the spanwise velocity component (figure 4
c). This topology has been observed in some of the previous numerical and experimental studies. For example, Rist & Augustin (Reference Rist and Augustin2006) induced such a peak–valley distribution in their direct numerical simulation (DNS) by imposing oblique disturbances in the boundary layer upstream of a flat plate separation bubble. In their experiments, Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016) note significant spanwise variations in coherent structures within a separation bubble developing on a symmetric aerofoil. For the current experiment, the characteristic wavelength of the spanwise variations seen in the time-averaged results in figure 4 is approximately
$y=0.39$
. Figure 4(b) depicts a three-dimensional outline of the separation bubble as well as several slices of wall-normal velocity. The results show minimal spanwise variation in the dividing streamline within the fore portion of the bubble, confirming the two-dimensional nature of the time-averaged incoming flow. In contrast, the time-averaged topology in the reattachment region shows distinct spanwise non-uniformities manifested by spatially periodic peaks and valleys, with a similar trend persisting in the fluctuation of the spanwise velocity component (figure 4
c). This topology has been observed in some of the previous numerical and experimental studies. For example, Rist & Augustin (Reference Rist and Augustin2006) induced such a peak–valley distribution in their direct numerical simulation (DNS) by imposing oblique disturbances in the boundary layer upstream of a flat plate separation bubble. In their experiments, Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016) note significant spanwise variations in coherent structures within a separation bubble developing on a symmetric aerofoil. For the current experiment, the characteristic wavelength of the spanwise variations seen in the time-averaged results in figure 4 is approximately
![]() $\unicode[STIX]{x1D706}_{r}=18.6$
. Given that no explicit oblique disturbances or distributed roughness are introduced, the observed stationary deformation may be attributed to spatially fixed disturbance sources in the experimental set-up, such as minute incoming flow non-uniformities and model imperfections, which condition the receptivity mechanism upstream the separation bubble.
$\unicode[STIX]{x1D706}_{r}=18.6$
. Given that no explicit oblique disturbances or distributed roughness are introduced, the observed stationary deformation may be attributed to spatially fixed disturbance sources in the experimental set-up, such as minute incoming flow non-uniformities and model imperfections, which condition the receptivity mechanism upstream the separation bubble.
Figure 5 compares the results obtained from planar and tomographic PIV by presenting mean streamwise velocity profiles at several streamwise locations. Here, the tomographic profiles shown are averaged along the spanwise direction. Profiles from the two measurements are in excellent agreement, with slight discrepancies becoming noticeable downstream of the mean reattachment region due to high velocity fluctuations.
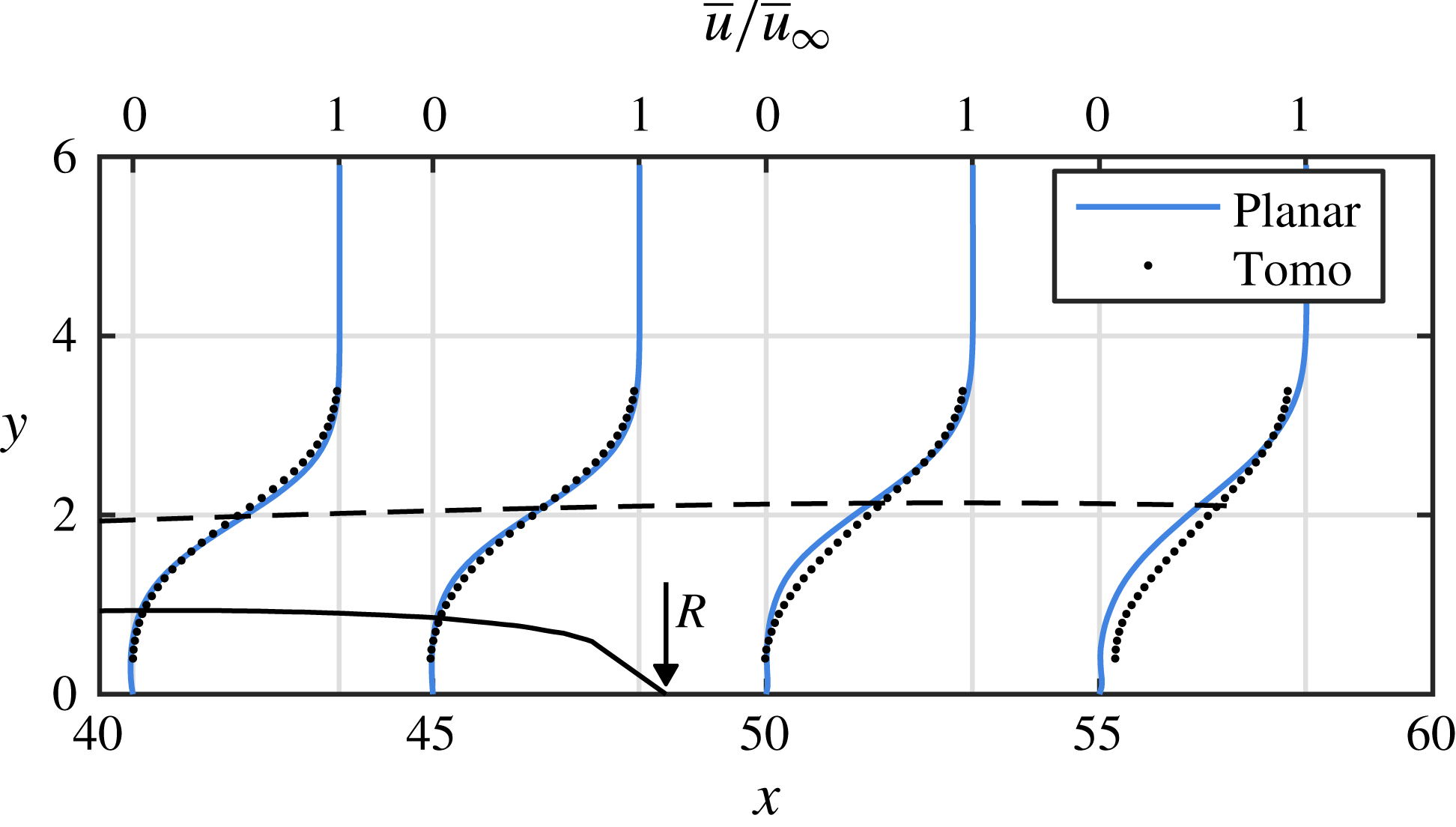
Figure 5. Time-averaged planar and tomographic PIV streamwise velocity measurements at several
![]() $x$
-stations. Note that the tomographic data have been averaged along the spanwise direction. Dashed line: displacement thickness calculated on the planar data.
$x$
-stations. Note that the tomographic data have been averaged along the spanwise direction. Dashed line: displacement thickness calculated on the planar data.
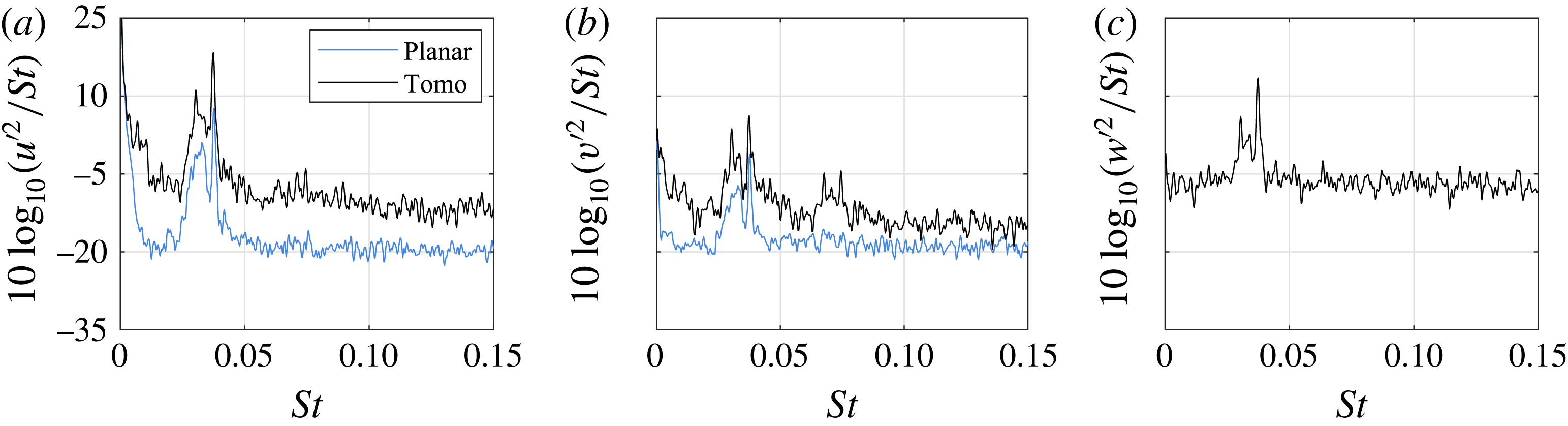
Figure 6. Power spectral density of the unforced LSB from both configurations estimated at
![]() $x=\bar{x}_{h}$
,
$x=\bar{x}_{h}$
,
![]() $y=\unicode[STIX]{x1D6FF}^{\ast }(\bar{x}_{h})$
and
$y=\unicode[STIX]{x1D6FF}^{\ast }(\bar{x}_{h})$
and
![]() $z=0$
. (a) Streamwise component fluctuation,
$z=0$
. (a) Streamwise component fluctuation,
![]() $u^{\prime }$
, (b) wall-normal component fluctuation,
$u^{\prime }$
, (b) wall-normal component fluctuation,
![]() $v$
and (c) spanwise component fluctuation,
$v$
and (c) spanwise component fluctuation,
![]() $w^{\prime }$
.
$w^{\prime }$
.
3.2 Spatio-temporal characteristics
The steady state features described earlier are directly related to the dynamic behaviour of the laminar separation bubble. First, the spectral content of velocity fluctuations is examined in figure 6. The spectra of the fluctuating velocity components
![]() $u^{\prime }$
,
$u^{\prime }$
,
![]() $v^{\prime }$
and
$v^{\prime }$
and
![]() $w^{\prime }$
are computed with the Welch method (Welch Reference Welch1967) with a frequency resolution of
$w^{\prime }$
are computed with the Welch method (Welch Reference Welch1967) with a frequency resolution of
![]() $St=2.7\times 10^{-4}$
(0.98 Hz). The corresponding temporal signal extracted at the mean maximum height streamwise location and the displacement thickness wall-normal distance. A dominant broadband peak is observed in the spectra of all the velocity components, located between
$St=2.7\times 10^{-4}$
(0.98 Hz). The corresponding temporal signal extracted at the mean maximum height streamwise location and the displacement thickness wall-normal distance. A dominant broadband peak is observed in the spectra of all the velocity components, located between
![]() $St=0.022$
(80 Hz) and
$St=0.022$
(80 Hz) and
![]() $St=0.047$
(170 Hz). The most prominent frequency corresponds to
$St=0.047$
(170 Hz). The most prominent frequency corresponds to
![]() $St_{0}=0.038$
(
$St_{0}=0.038$
(
![]() $\tilde{f}_{0}=136$
Hz) which is later confirmed to correspond to the frequency of the most unstable mode (§ 4.2). Hence, it is referred to as the fundamental frequency
$\tilde{f}_{0}=136$
Hz) which is later confirmed to correspond to the frequency of the most unstable mode (§ 4.2). Hence, it is referred to as the fundamental frequency
![]() $(St_{0})$
. Several other peaks are identified in the vicinity of the fundamental frequency, albeit one order of magnitude weaker, and are commonly observed in natural transition studies due to spectral content of background disturbances in a given experimental facility. When expressed in terms of dimensionless frequency,
$(St_{0})$
. Several other peaks are identified in the vicinity of the fundamental frequency, albeit one order of magnitude weaker, and are commonly observed in natural transition studies due to spectral content of background disturbances in a given experimental facility. When expressed in terms of dimensionless frequency,
![]() $\unicode[STIX]{x1D714}^{\ast }=0.25\unicode[STIX]{x1D6FF}_{w}(2\unicode[STIX]{x03C0}\tilde{f})/\bar{U}$
(Ho & Huerre Reference Ho and Huerre1984), based on vorticity thickness
$\unicode[STIX]{x1D714}^{\ast }=0.25\unicode[STIX]{x1D6FF}_{w}(2\unicode[STIX]{x03C0}\tilde{f})/\bar{U}$
(Ho & Huerre Reference Ho and Huerre1984), based on vorticity thickness
![]() $(\unicode[STIX]{x1D6FF}_{w})$
and the average velocity of the shear bounding limits
$(\unicode[STIX]{x1D6FF}_{w})$
and the average velocity of the shear bounding limits
![]() $(\bar{U})$
, the fundamental frequency is
$(\bar{U})$
, the fundamental frequency is
![]() $\unicode[STIX]{x1D714}_{0}^{\ast }=0.21$
. This value is within the expected range for Kelvin–Helmholtz instability in free shear layers (Ho & Huerre Reference Ho and Huerre1984)
$\unicode[STIX]{x1D714}_{0}^{\ast }=0.21$
. This value is within the expected range for Kelvin–Helmholtz instability in free shear layers (Ho & Huerre Reference Ho and Huerre1984)
![]() $(0.21<\unicode[STIX]{x1D714}^{\ast }<0.222)$
and agrees well with relevant studies on LSBs (Pauley, Moin & Reynolds Reference Pauley, Moin and Reynolds1990; Watmuff Reference Watmuff1999; Simoni et al.
Reference Simoni, Ubaldi, Zunino and Bertini2012).
$(0.21<\unicode[STIX]{x1D714}^{\ast }<0.222)$
and agrees well with relevant studies on LSBs (Pauley, Moin & Reynolds Reference Pauley, Moin and Reynolds1990; Watmuff Reference Watmuff1999; Simoni et al.
Reference Simoni, Ubaldi, Zunino and Bertini2012).
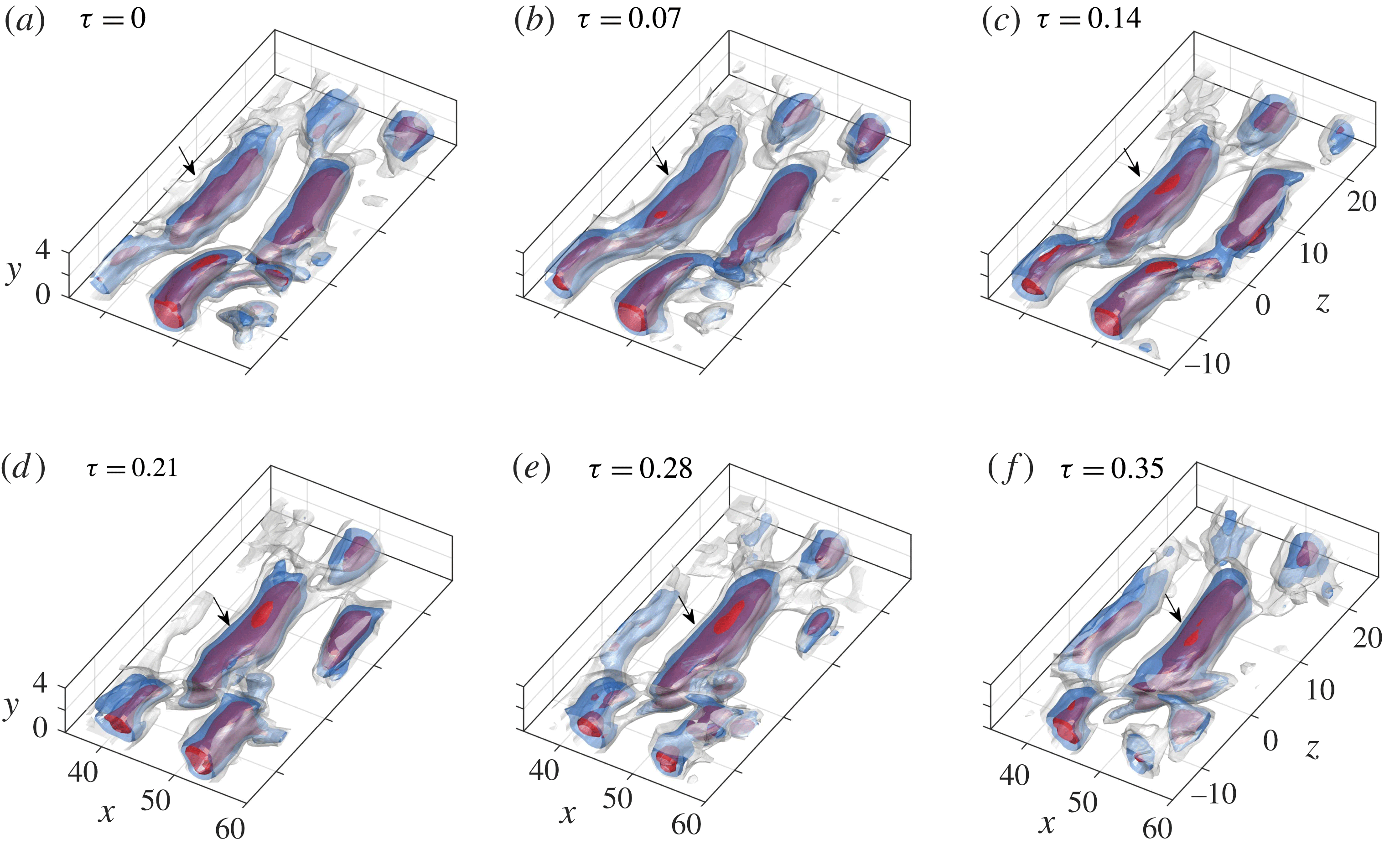
Figure 7. Unforced bubble instantaneous
![]() $Q$
-criterion series, separated by
$Q$
-criterion series, separated by
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}=0.14$
. Grey, blue and red iso-surfaces correspond to
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}=0.14$
. Grey, blue and red iso-surfaces correspond to
![]() $Q=0$
, 0.002 and 0.006, respectively. Arrows mark the same vortex convecting through the snapshots.
$Q=0$
, 0.002 and 0.006, respectively. Arrows mark the same vortex convecting through the snapshots.
The tomographic configuration and vortex identification criteria allow exploration of the three-dimensional coherent structures in the LSB. Instantaneous snapshots of the unforced LSB are shown in figure 7, where the structures are identified using iso-surfaces of
![]() $Q$
-criterion (Hunt, Wray & Moin Reference Hunt, Wray and Moin1988). An animated sequence is provided as supplementary material (movie 1) available at https://doi.org/10.1017/jfm.2018.91. The results show that in the aft portion of the bubble (figure 4
a), vortical structures exhibit strong spanwise deformations, with notable staggering in the
$Q$
-criterion (Hunt, Wray & Moin Reference Hunt, Wray and Moin1988). An animated sequence is provided as supplementary material (movie 1) available at https://doi.org/10.1017/jfm.2018.91. The results show that in the aft portion of the bubble (figure 4
a), vortical structures exhibit strong spanwise deformations, with notable staggering in the
![]() $x$
–
$x$
–
![]() $z$
plane. Similar vortex distribution is observed in the DNS results of Marxen & Henningson (Reference Marxen and Henningson2011) where the separation bubble is asymmetrically forced with oblique waves, and in the experiments of Burgmann & Schröder (Reference Burgmann and Schröder2008) and Nati et al. (Reference Nati, de Kat, Scarano and van Oudheusden2015).
$z$
plane. Similar vortex distribution is observed in the DNS results of Marxen & Henningson (Reference Marxen and Henningson2011) where the separation bubble is asymmetrically forced with oblique waves, and in the experiments of Burgmann & Schröder (Reference Burgmann and Schröder2008) and Nati et al. (Reference Nati, de Kat, Scarano and van Oudheusden2015).

Figure 8. Unforced bubble instantaneous
![]() $Q$
-criterion snapshot. (a) Grey, blue and red iso-surfaces correspond to
$Q$
-criterion snapshot. (a) Grey, blue and red iso-surfaces correspond to
![]() $Q=0$
, 0.002 and 0.006 respectively. (b)
$Q=0$
, 0.002 and 0.006 respectively. (b)
![]() $x$
–
$x$
–
![]() $y$
plane at
$y$
plane at
![]() $z=4.5$
, (c)
$z=4.5$
, (c)
![]() $x$
–
$x$
–
![]() $z$
plane at
$z$
plane at
![]() $x=48.5$
. Dashed lines: monitor lines at the measurement volume centre,
$x=48.5$
. Dashed lines: monitor lines at the measurement volume centre,
![]() $x=48.5$
,
$x=48.5$
,
![]() $y=1.8$
and
$y=1.8$
and
![]() $z=4.5$
, solid lines:
$z=4.5$
, solid lines:
![]() $Q\geqslant 0$
, dash-dotted lines:
$Q\geqslant 0$
, dash-dotted lines:
![]() $Q<0$
.
$Q<0$
.
An additional feature of the flow field is the presence of vortex filaments which connect the staggered vortex cores, indicated by arrows in figure 8(a). Similar topological features persist through the shedding cycles, as illustrated by the snapshots shown in figure 7. The results suggest that the locations of dominant deformations do not shift significantly in the spanwise direction from cycle to cycle, resulting in distinct peaks and valleys in the time-averaged outline of the aft part of the LSB (figure 4 b).
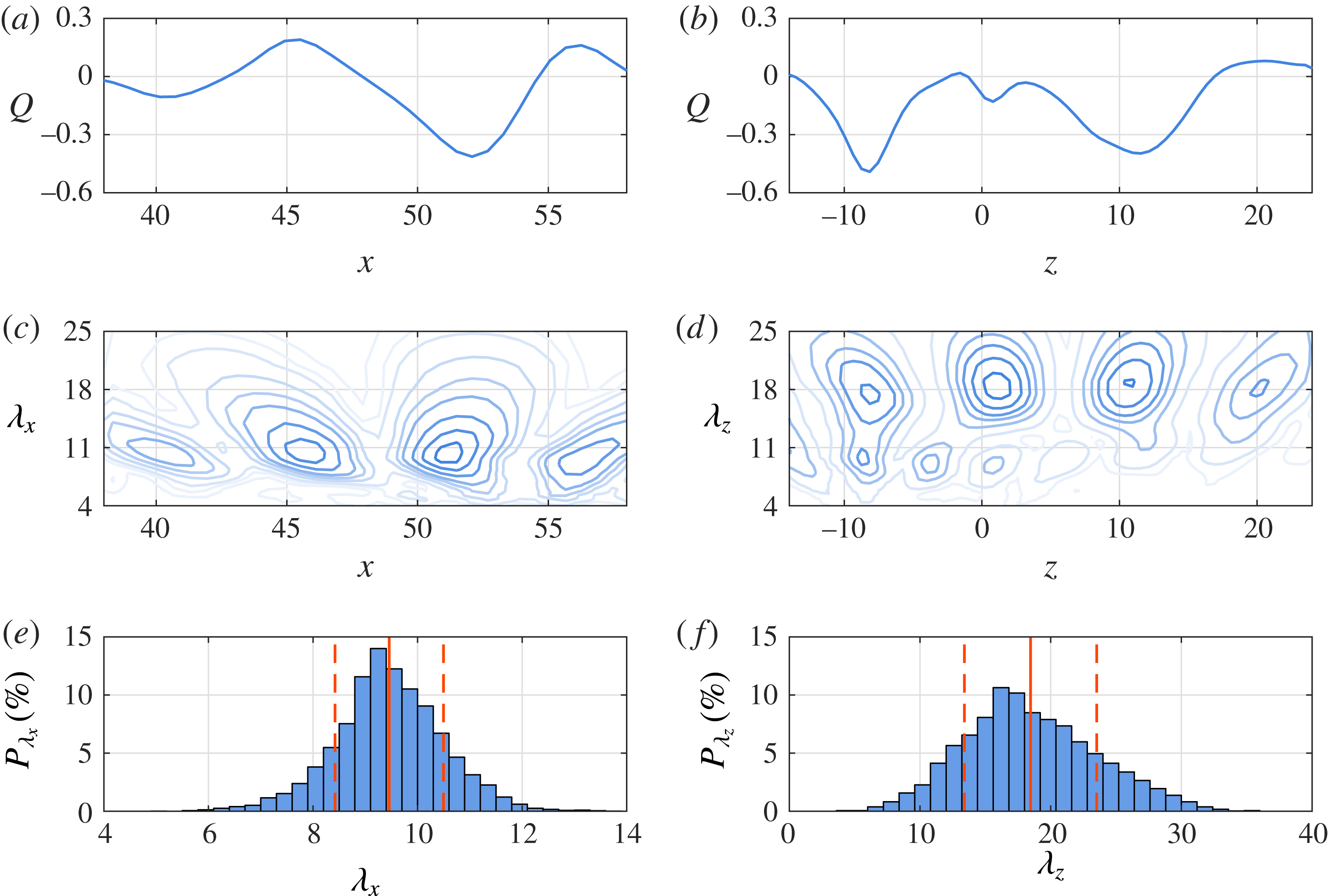
Figure 9. Columns represent streamwise and spanwise quantities respectively. (a,b)
![]() $Q$
-criterion along the spanwise monitor line (figure 8). (c,d) Corresponding wavelet coefficients. (e,f) Wavelength probability distributions. The vertical dashed lines indicate the standard deviation with respect to the mean value.
$Q$
-criterion along the spanwise monitor line (figure 8). (c,d) Corresponding wavelet coefficients. (e,f) Wavelength probability distributions. The vertical dashed lines indicate the standard deviation with respect to the mean value.
Given the limited spanwise extent of the field of view relative to the wavelength of the spanwise deformations, determination of the streamwise
![]() $(\unicode[STIX]{x1D706}_{x})$
and spanwise
$(\unicode[STIX]{x1D706}_{x})$
and spanwise
![]() $(\unicode[STIX]{x1D706}_{z})$
wavelengths is performed through spatial wavelet analysis (Daubechies Reference Daubechies1992; Michelis et al.
Reference Michelis, Kotsonis and Yarusevych2017). At each recorded time instant, the total
$(\unicode[STIX]{x1D706}_{z})$
wavelengths is performed through spatial wavelet analysis (Daubechies Reference Daubechies1992; Michelis et al.
Reference Michelis, Kotsonis and Yarusevych2017). At each recorded time instant, the total
![]() $Q$
-criterion value is computed along the dashed streamwise and spanwise monitor lines indicated in figure 8. The two lines intersect at the centre of the measurement volume (
$Q$
-criterion value is computed along the dashed streamwise and spanwise monitor lines indicated in figure 8. The two lines intersect at the centre of the measurement volume (
![]() $x=48.5$
,
$x=48.5$
,
![]() $y=1.8$
,
$y=1.8$
,
![]() $z=4.5$
). Exemplary instantaneous spatial distributions of
$z=4.5$
). Exemplary instantaneous spatial distributions of
![]() $Q$
in streamwise and spanwise directions are shown in figure 9(a,b), along with their respective wavelet coefficients (figure 9
c,d). The dominant wavelength is estimated based on the maximum wavelet coefficient at each time instant. This procedure is repeated for all instantaneous snapshots, and the results are presented in figure 9(e,f) as probability distributions. It can be seen that both
$Q$
in streamwise and spanwise directions are shown in figure 9(a,b), along with their respective wavelet coefficients (figure 9
c,d). The dominant wavelength is estimated based on the maximum wavelet coefficient at each time instant. This procedure is repeated for all instantaneous snapshots, and the results are presented in figure 9(e,f) as probability distributions. It can be seen that both
![]() $\unicode[STIX]{x1D706}_{x}$
and
$\unicode[STIX]{x1D706}_{x}$
and
![]() $\unicode[STIX]{x1D706}_{z}$
are distributed about central values corresponding to
$\unicode[STIX]{x1D706}_{z}$
are distributed about central values corresponding to
![]() $\bar{\unicode[STIX]{x1D706}}_{x}=9.4$
and
$\bar{\unicode[STIX]{x1D706}}_{x}=9.4$
and
![]() $\bar{\unicode[STIX]{x1D706}}_{z}=18.2$
, with standard deviations of
$\bar{\unicode[STIX]{x1D706}}_{z}=18.2$
, with standard deviations of
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D706}_{x}}=1.1$
and
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D706}_{x}}=1.1$
and
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D706}_{z}}=6.7$
, respectively. The average spanwise wavelength is in excellent agreement with the wavelength of spanwise deformations seen in the time-averaged outline of the aft portion of the LSB (
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D706}_{z}}=6.7$
, respectively. The average spanwise wavelength is in excellent agreement with the wavelength of spanwise deformations seen in the time-averaged outline of the aft portion of the LSB (
![]() $\unicode[STIX]{x1D706}_{r}=18.6$
, figure 4). Hence,
$\unicode[STIX]{x1D706}_{r}=18.6$
, figure 4). Hence,
![]() $\unicode[STIX]{x1D706}_{x_{0}}=9.4$
and
$\unicode[STIX]{x1D706}_{x_{0}}=9.4$
and
![]() $\unicode[STIX]{x1D706}_{z_{0}}=18.2$
are used as the fundamental streamwise and spanwise wavelengths, respectively, for the rest of the analysis. The ratio of characteristic spanwise to streamwise wavelengths,
$\unicode[STIX]{x1D706}_{z_{0}}=18.2$
are used as the fundamental streamwise and spanwise wavelengths, respectively, for the rest of the analysis. The ratio of characteristic spanwise to streamwise wavelengths,
![]() $\unicode[STIX]{x1D706}_{z_{0}}/\unicode[STIX]{x1D706}_{x_{0}}$
, is equal to 1.94, yielding an obliqueness angle of
$\unicode[STIX]{x1D706}_{z_{0}}/\unicode[STIX]{x1D706}_{x_{0}}$
, is equal to 1.94, yielding an obliqueness angle of
![]() $27^{\circ }$
. This is comparable to the results of Rist & Augustin (Reference Rist and Augustin2006), Marxen & Henningson (Reference Marxen and Henningson2011) and Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016) who report wavelength ratios of 1.92, 2.4 and 2.5, respectively.
$27^{\circ }$
. This is comparable to the results of Rist & Augustin (Reference Rist and Augustin2006), Marxen & Henningson (Reference Marxen and Henningson2011) and Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016) who report wavelength ratios of 1.92, 2.4 and 2.5, respectively.
To assess the existence of various spanwise modes within the imaged tomographic PIV domain in the unforced bubble, a double Fourier analysis in space and time is performed on the wall-normal velocity component, extracted along the spanwise monitor line at the centre of the measurement volume (
![]() $x=48.5$
,
$x=48.5$
,
![]() $y=1.8$
, see figure 8). The power spectral density estimate is shown in figure 10, where
$y=1.8$
, see figure 8). The power spectral density estimate is shown in figure 10, where
![]() $h$
and
$h$
and
![]() $k$
are frequencies and wavelengths scaled with the fundamental ones,
$k$
are frequencies and wavelengths scaled with the fundamental ones,
![]() $St_{0}$
and
$St_{0}$
and
![]() $\unicode[STIX]{x1D706}_{z_{0}}$
, respectively. Two prominent peaks are observed in figure 10(a,c), located at exactly
$\unicode[STIX]{x1D706}_{z_{0}}$
, respectively. Two prominent peaks are observed in figure 10(a,c), located at exactly
![]() $(h,k)=(1,\pm 1)$
, confirming the observations of the spectral and wavelet analyses. In addition, there is elevated spectral density at
$(h,k)=(1,\pm 1)$
, confirming the observations of the spectral and wavelet analyses. In addition, there is elevated spectral density at
![]() $(1,0)$
, identified as a valley between the two peaks (figure 10
c). As discussed in the following sections, the band encompassing the peaks and the valley is attributed to a pair of oblique modes and a normal mode, respectively. In addition, a band of modes with a peak centred at
$(1,0)$
, identified as a valley between the two peaks (figure 10
c). As discussed in the following sections, the band encompassing the peaks and the valley is attributed to a pair of oblique modes and a normal mode, respectively. In addition, a band of modes with a peak centred at
![]() $(0,0)$
is observed in the frequency–wavelength spectrum (figure 10
a,b), suggesting that the interaction between the oblique pair and the normal mode is largely linear, without exhibiting sub-harmonic resonance. The wide range of
$(0,0)$
is observed in the frequency–wavelength spectrum (figure 10
a,b), suggesting that the interaction between the oblique pair and the normal mode is largely linear, without exhibiting sub-harmonic resonance. The wide range of
![]() $k$
at which the frequency–wavelength spectrum band extends at
$k$
at which the frequency–wavelength spectrum band extends at
![]() $h=1$
(figure 10
a,b) indicates the non-deterministic development of oblique modes, explaining the histogram distribution of both streamwise and spanwise wavelengths shown on figure 9.
$h=1$
(figure 10
a,b) indicates the non-deterministic development of oblique modes, explaining the histogram distribution of both streamwise and spanwise wavelengths shown on figure 9.
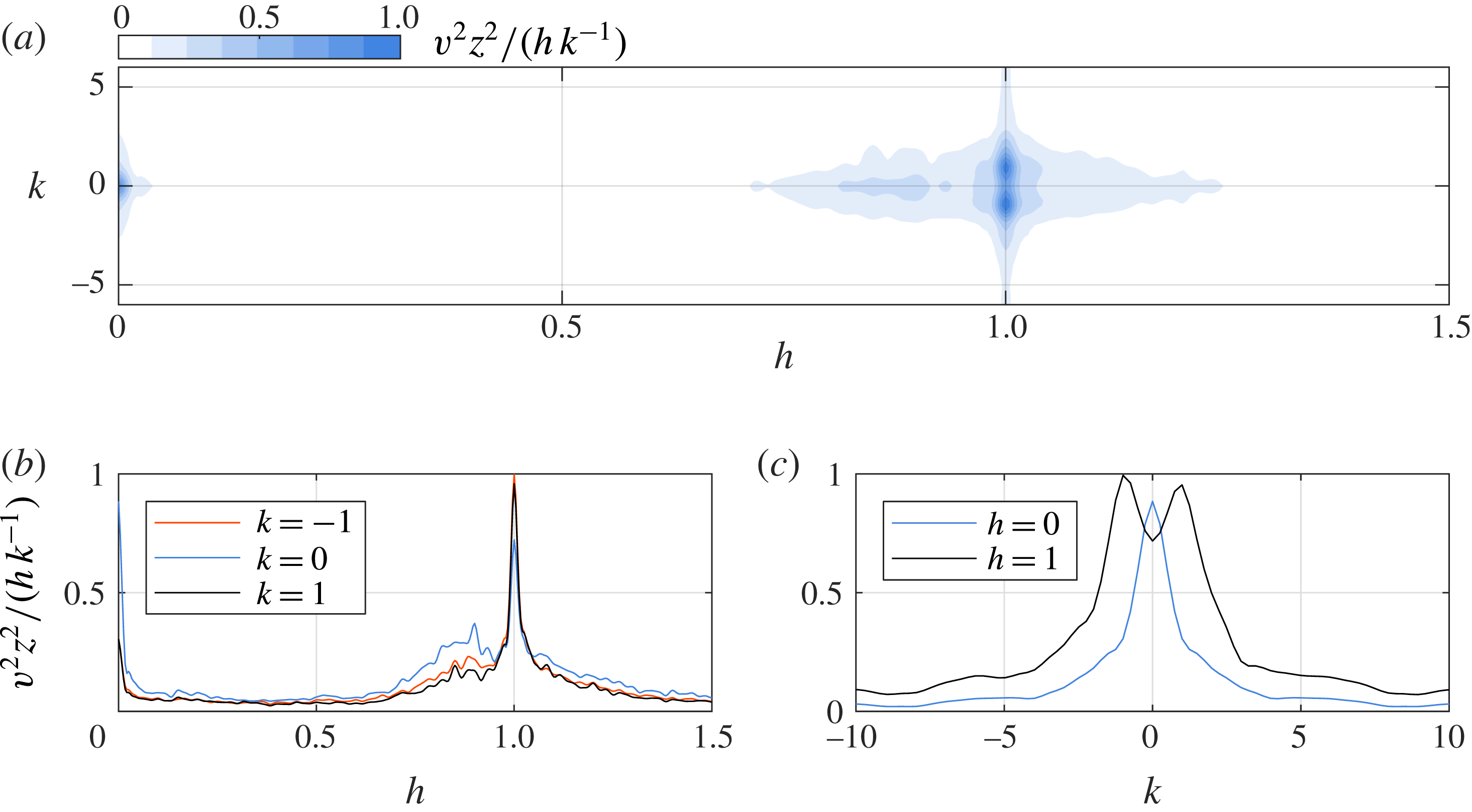
Figure 10. (a) Frequency–wavelength
![]() $(h,k)$
power spectral density estimate, normalised with its maximum value. (b) Slices of the spectrum along
$(h,k)$
power spectral density estimate, normalised with its maximum value. (b) Slices of the spectrum along
![]() $k=-1,0$
, and 1. (c) Slices of the spectrum along
$k=-1,0$
, and 1. (c) Slices of the spectrum along
![]() $h=0$
, and 1.
$h=0$
, and 1.
4 Origin of spanwise vortex deformations
4.1 Boundary layer calculations upstream the LSB
In order to shed light on the mechanism responsible for the observed spanwise topology of vortical structures (figure 8), it is instructive to examine the stability characteristics of the incoming boundary layer and the fore portion of the separation bubble. Given the experimental field of view and resolution limitations, the laminar boundary layer equations (Schlichting & Gersten Reference Schlichting and Gersten2000) are solved numerically using an implicit solver to characterise the velocity in the boundary layer upstream of separation. The imposed streamwise pressure gradient is estimated based on the measured pressure distribution (figure 2
a). The solution is marched from the location of the most upstream pressure tap, at which the inflow boundary layer profile is approximated with a Falkner Skan analytical solution. The subsequent marching is carried out until the expected failure of the numerical solution is observed just upstream of separation. The predicted separation point appears at
![]() $x=1.6$
, which is approximately 1 % of the plate length upstream of the experimentally determined separation location
$x=1.6$
, which is approximately 1 % of the plate length upstream of the experimentally determined separation location
![]() $(x_{s}=6.3)$
. The results of the computations are validated through a direct comparison with measured data at
$(x_{s}=6.3)$
. The results of the computations are validated through a direct comparison with measured data at
![]() $x=1.6$
(figure 11). The agreement between the results is remarkable, with the only noteworthy deviation observed in the second wall-normal derivative in the proximity of the wall (
$x=1.6$
(figure 11). The agreement between the results is remarkable, with the only noteworthy deviation observed in the second wall-normal derivative in the proximity of the wall (
![]() $y<0.5$
, figure 11
c). In addition, the corresponding integral boundary layer parameters for BLS and PIV compare as
$y<0.5$
, figure 11
c). In addition, the corresponding integral boundary layer parameters for BLS and PIV compare as
![]() $\unicode[STIX]{x1D6FF}^{\ast }=0.88$
and 0.87, and
$\unicode[STIX]{x1D6FF}^{\ast }=0.88$
and 0.87, and
![]() $H=3.54$
and 3.41, respectively.
$H=3.54$
and 3.41, respectively.
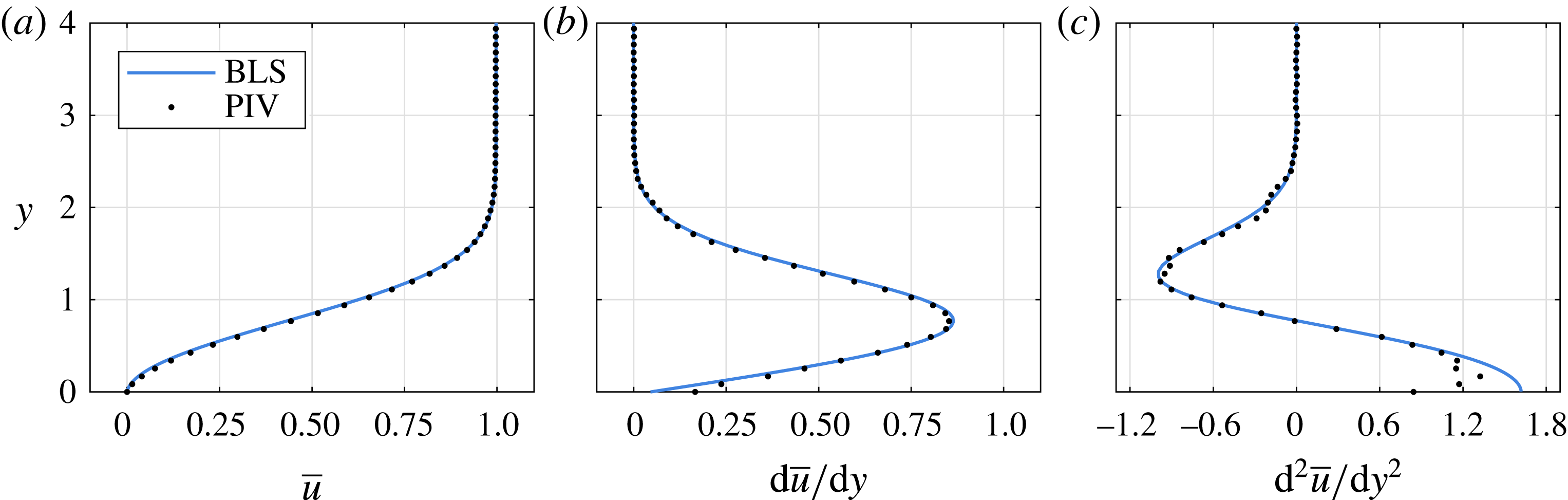
Figure 11. Comparison between the numerical boundary layer solution and PIV measurements, at
![]() $x=1.6$
. (a) Streamwise velocity profile, (b) first derivative and (c) second derivative of streamwise velocity along the wall-normal direction.
$x=1.6$
. (a) Streamwise velocity profile, (b) first derivative and (c) second derivative of streamwise velocity along the wall-normal direction.

Figure 12. Comparison between LST and PIV of (a)
![]() $N$
factor and normalised (b) streamwise and (c) wall-normal disturbance profiles. The results are presented at
$N$
factor and normalised (b) streamwise and (c) wall-normal disturbance profiles. The results are presented at
![]() $x=40$
for mode
$x=40$
for mode
![]() $(1,0)$
. The experimental data have been filtered with a narrow bandpass filter about the fundamental frequency
$(1,0)$
. The experimental data have been filtered with a narrow bandpass filter about the fundamental frequency
![]() $St_{0}=0.038$
. The black circle indicates the location where
$St_{0}=0.038$
. The black circle indicates the location where
![]() $\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D70E}_{u}}=0.01\,\%$
, at which the
$\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D70E}_{u}}=0.01\,\%$
, at which the
![]() $N$
factors from LST and PIV are matched.
$N$
factors from LST and PIV are matched.
4.2 Linear stability analysis on the composite flow field
Linear stability theory calculations are performed on the composite flow field consisting of the numerically calculated boundary layer in the region
![]() $-140.4\leqslant x\leqslant 1.6$
and the PIV measured flow field in the region
$-140.4\leqslant x\leqslant 1.6$
and the PIV measured flow field in the region
![]() $1.6\leqslant x\leqslant 56.9$
. This analysis is in line with the one performed by Dovgal, Kozlov & Michalke (Reference Dovgal, Kozlov and Michalke1994) on boundary layers with adverse pressure gradients. The primary goal is to investigate the existence and growth of oblique modes upstream of separation that may give rise to spanwise deformations of vortex filaments in the LSB (figure 8). More specifically, the focus is on the relative amplification of oblique modes with respect to normal modes. The typical assumptions of locally parallel, spanwise-uniform flow and small amplitude perturbations are invoked (Mack Reference Mack1984; van Ingen Reference van Ingen2008). Consequently, the spanwise growth rate,
$1.6\leqslant x\leqslant 56.9$
. This analysis is in line with the one performed by Dovgal, Kozlov & Michalke (Reference Dovgal, Kozlov and Michalke1994) on boundary layers with adverse pressure gradients. The primary goal is to investigate the existence and growth of oblique modes upstream of separation that may give rise to spanwise deformations of vortex filaments in the LSB (figure 8). More specifically, the focus is on the relative amplification of oblique modes with respect to normal modes. The typical assumptions of locally parallel, spanwise-uniform flow and small amplitude perturbations are invoked (Mack Reference Mack1984; van Ingen Reference van Ingen2008). Consequently, the spanwise growth rate,
![]() $\unicode[STIX]{x1D6FD}_{i}$
, and the spanwise velocity component,
$\unicode[STIX]{x1D6FD}_{i}$
, and the spanwise velocity component,
![]() $\bar{w}$
, are set to zero in the Orr–Sommerfeld equation,
$\bar{w}$
, are set to zero in the Orr–Sommerfeld equation,
Further assessment of nonlinearity in the separated shear layer is performed by comparing
![]() $N$
factors for mode
$N$
factors for mode
![]() $(1,0)$
between the LST analysis and the planar PIV measurements (figure 12
a). For the required computations, the experimentally measured velocity fields are filtered with a sixth-order zero phase-lag digital bandpass filter, centred at the fundamental frequency
$(1,0)$
between the LST analysis and the planar PIV measurements (figure 12
a). For the required computations, the experimentally measured velocity fields are filtered with a sixth-order zero phase-lag digital bandpass filter, centred at the fundamental frequency
![]() $St_{0}=0.038$
and limited within
$St_{0}=0.038$
and limited within
![]() $\pm 0.02St_{0}$
. The amplification factor is subsequently determined by considering the maximum standard deviation of the filtered streamwise velocity component at each streamwise location, formulated as
$\pm 0.02St_{0}$
. The amplification factor is subsequently determined by considering the maximum standard deviation of the filtered streamwise velocity component at each streamwise location, formulated as
![]() $N=\text{ln}(\unicode[STIX]{x1D70E}_{u})+C$
. Here,
$N=\text{ln}(\unicode[STIX]{x1D70E}_{u})+C$
. Here,
![]() $C$
corresponds to an offset, selected at the streamwise location where the estimated
$C$
corresponds to an offset, selected at the streamwise location where the estimated
![]() $\unicode[STIX]{x1D70E}_{u}$
becomes higher than the PIV measurement error
$\unicode[STIX]{x1D70E}_{u}$
becomes higher than the PIV measurement error
![]() $(\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D70E}_{u}}=0.01\,\%)$
. This location is marked by a circle in figure 12(a), upstream which the
$(\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D70E}_{u}}=0.01\,\%)$
. This location is marked by a circle in figure 12(a), upstream which the
![]() $N$
factor curve flattens, indicating the noise limit of PIV measurements. Nonetheless, the agreement between the LST and PIV
$N$
factor curve flattens, indicating the noise limit of PIV measurements. Nonetheless, the agreement between the LST and PIV
![]() $N$
factor is remarkable up to approximately the maximum bubble height, suggesting that the pertinent fluctuations can be approximated by a linear growth model, similar to the results of Yarusevych & Kotsonis (Reference Yarusevych and Kotsonis2017a
). In turn, figure 12(b,c) depicts typical streamwise and wall-normal disturbance profiles, normalised with the maximum value. Once again, the comparison is done for mode
$N$
factor is remarkable up to approximately the maximum bubble height, suggesting that the pertinent fluctuations can be approximated by a linear growth model, similar to the results of Yarusevych & Kotsonis (Reference Yarusevych and Kotsonis2017a
). In turn, figure 12(b,c) depicts typical streamwise and wall-normal disturbance profiles, normalised with the maximum value. Once again, the comparison is done for mode
![]() $(1,0)$
between LST and the bandpass filtered experimental data. Evidently, the results show a very good agreement with the same range as the amplification factor predictions considered earlier. Due to the observed agreement of both the
$(1,0)$
between LST and the bandpass filtered experimental data. Evidently, the results show a very good agreement with the same range as the amplification factor predictions considered earlier. Due to the observed agreement of both the
![]() $N$
factor and the disturbance profiles, it can be concluded that LST is suitable for determining stability characteristics in the current investigation.
$N$
factor and the disturbance profiles, it can be concluded that LST is suitable for determining stability characteristics in the current investigation.
The stability diagram for
![]() $\unicode[STIX]{x1D6FD}_{r}=0$
, calculated on the combination of numerical and experimental results, is shown in figure 13. The results show a continuous stability spectrum between the attached and separated flow regions, confirming the earlier conjectures of inherent interrelation between the stability characteristics of the boundary layer and the LSB (Dovgal et al.
Reference Dovgal, Kozlov and Michalke1994; Diwan & Ramesh Reference Diwan and Ramesh2009; Michelis et al.
Reference Michelis, Kotsonis and Yarusevych2017), with similar features also observed in recent results of Marxen et al. (Reference Marxen, Kotapati, Mital and Zaki2015) and Yarusevych & Kotsonis (Reference Yarusevych and Kotsonis2017b
). The critical point is located in the adverse pressure gradient region (figure 2
a) at
$\unicode[STIX]{x1D6FD}_{r}=0$
, calculated on the combination of numerical and experimental results, is shown in figure 13. The results show a continuous stability spectrum between the attached and separated flow regions, confirming the earlier conjectures of inherent interrelation between the stability characteristics of the boundary layer and the LSB (Dovgal et al.
Reference Dovgal, Kozlov and Michalke1994; Diwan & Ramesh Reference Diwan and Ramesh2009; Michelis et al.
Reference Michelis, Kotsonis and Yarusevych2017), with similar features also observed in recent results of Marxen et al. (Reference Marxen, Kotapati, Mital and Zaki2015) and Yarusevych & Kotsonis (Reference Yarusevych and Kotsonis2017b
). The critical point is located in the adverse pressure gradient region (figure 2
a) at
![]() $x_{c}=-47$
, approximately one bubble length upstream of
$x_{c}=-47$
, approximately one bubble length upstream of
![]() $x_{s}$
. The frequency corresponding to the most unstable growth rate, marked by the dashed line, decreases towards the separation location. Past the separation point, the maximum growth rate increases significantly, and the associated frequency begins to increase. The maximum amplification factor is achieved in the vicinity of the mean maximum height and is
$x_{s}$
. The frequency corresponding to the most unstable growth rate, marked by the dashed line, decreases towards the separation location. Past the separation point, the maximum growth rate increases significantly, and the associated frequency begins to increase. The maximum amplification factor is achieved in the vicinity of the mean maximum height and is
![]() $N=7.2$
. The corresponding frequency effectively matches the fundamental frequency
$N=7.2$
. The corresponding frequency effectively matches the fundamental frequency
![]() $St_{0}=0.038$
(136 Hz) estimated from the velocity spectra (figure 6). Diwan & Ramesh (Reference Diwan and Ramesh2012) propose that the reason behind the remarkable agreement of linear stability analysis with experimental observations is due to the baseline (time-averaged) flow field being nearly parallel. It must be noted, however, that the presence of a single primary mode would lead to the same observation.
$St_{0}=0.038$
(136 Hz) estimated from the velocity spectra (figure 6). Diwan & Ramesh (Reference Diwan and Ramesh2012) propose that the reason behind the remarkable agreement of linear stability analysis with experimental observations is due to the baseline (time-averaged) flow field being nearly parallel. It must be noted, however, that the presence of a single primary mode would lead to the same observation.

Figure 13. Iso-contours of streamwise growth rates
![]() $(\unicode[STIX]{x1D6FC}_{i})$
for
$(\unicode[STIX]{x1D6FC}_{i})$
for
![]() $\unicode[STIX]{x1D6FD}_{r}=0$
as estimated through the boundary layer solver (left) and through the planar PIV measurements (right), in steps of 0.05. Solid lines:
$\unicode[STIX]{x1D6FD}_{r}=0$
as estimated through the boundary layer solver (left) and through the planar PIV measurements (right), in steps of 0.05. Solid lines:
![]() $\unicode[STIX]{x1D6FC}_{i}\leqslant 0$
, dotted lines:
$\unicode[STIX]{x1D6FC}_{i}\leqslant 0$
, dotted lines:
![]() $\unicode[STIX]{x1D6FC}_{i}>0$
, dashed line: minimum
$\unicode[STIX]{x1D6FC}_{i}>0$
, dashed line: minimum
![]() $\unicode[STIX]{x1D6FC}_{i}$
.
$\unicode[STIX]{x1D6FC}_{i}$
.
![]() $x_{c}$
marks the critical streamwise position where disturbances first become unstable. S and R mark separation and reattachment, respectively.
$x_{c}$
marks the critical streamwise position where disturbances first become unstable. S and R mark separation and reattachment, respectively.
The streamwise growth rate,
![]() $\unicode[STIX]{x1D6FC}_{i}$
, with respect to the spanwise wavenumber and wavelength at the mean maximum height, is shown in figure 14(a). It is noted that an increase in
$\unicode[STIX]{x1D6FC}_{i}$
, with respect to the spanwise wavenumber and wavelength at the mean maximum height, is shown in figure 14(a). It is noted that an increase in
![]() $\unicode[STIX]{x1D6FD}_{r}$
(or a decrease in
$\unicode[STIX]{x1D6FD}_{r}$
(or a decrease in
![]() $\unicode[STIX]{x1D706}_{z}$
) results in the reduction of the most unstable wave frequency. The critical spanwise wavenumber at which disturbances become unstable is
$\unicode[STIX]{x1D706}_{z}$
) results in the reduction of the most unstable wave frequency. The critical spanwise wavenumber at which disturbances become unstable is
![]() $\unicode[STIX]{x1D6FD}_{r_{c}}=2.2$
(
$\unicode[STIX]{x1D6FD}_{r_{c}}=2.2$
(
![]() $\unicode[STIX]{x1D706}_{z_{c}}=5.7$
). In addition, for spanwise wavenumbers lower than approximately
$\unicode[STIX]{x1D706}_{z_{c}}=5.7$
). In addition, for spanwise wavenumbers lower than approximately
![]() $\unicode[STIX]{x1D6FD}_{r}<0.8$
(
$\unicode[STIX]{x1D6FD}_{r}<0.8$
(
![]() $\unicode[STIX]{x1D706}_{z}>15$
), the frequency of the predicted unstable waves remains largely invariant up to
$\unicode[STIX]{x1D706}_{z}>15$
), the frequency of the predicted unstable waves remains largely invariant up to
![]() $\unicode[STIX]{x1D6FD}_{r}=0$
. The maximum growth rate also increases as
$\unicode[STIX]{x1D6FD}_{r}=0$
. The maximum growth rate also increases as
![]() $\unicode[STIX]{x1D6FD}_{r}$
decreases to zero, suggesting that, at this stage, the most unstable modes are normal TS waves that undergo convective amplification. The same conclusion can be drawn by tracing the streamwise growth rate and amplification factor with respect to the wave angle,
$\unicode[STIX]{x1D6FD}_{r}$
decreases to zero, suggesting that, at this stage, the most unstable modes are normal TS waves that undergo convective amplification. The same conclusion can be drawn by tracing the streamwise growth rate and amplification factor with respect to the wave angle,
![]() $\unicode[STIX]{x1D717}=\text{tan}^{-1}(\unicode[STIX]{x1D6FD}_{r}/\unicode[STIX]{x1D6FC}_{r})$
, shown in figures 14(b) and 14(c), respectively, for
$\unicode[STIX]{x1D717}=\text{tan}^{-1}(\unicode[STIX]{x1D6FD}_{r}/\unicode[STIX]{x1D6FC}_{r})$
, shown in figures 14(b) and 14(c), respectively, for
![]() $St_{0}$
at several streamwise stations within the bubble. Once again, the most unstable conditions correspond to
$St_{0}$
at several streamwise stations within the bubble. Once again, the most unstable conditions correspond to
![]() $\unicode[STIX]{x1D717}=0^{\circ }$
, i.e. to mode
$\unicode[STIX]{x1D717}=0^{\circ }$
, i.e. to mode
![]() $(1,0)$
.
$(1,0)$
.

Figure 14. (a) Streamwise growth rate,
![]() $\unicode[STIX]{x1D6FC}_{i}$
with respect to spanwise wavenumber and wavelength at
$\unicode[STIX]{x1D6FC}_{i}$
with respect to spanwise wavenumber and wavelength at
![]() $\bar{x}_{h}$
, in steps of 0.1. Solid lines:
$\bar{x}_{h}$
, in steps of 0.1. Solid lines:
![]() $\unicode[STIX]{x1D6FC}_{i}\leqslant 0$
, dotted lines:
$\unicode[STIX]{x1D6FC}_{i}\leqslant 0$
, dotted lines:
![]() $\unicode[STIX]{x1D6FC}_{i}>0$
, dashed line: minimum
$\unicode[STIX]{x1D6FC}_{i}>0$
, dashed line: minimum
![]() $\unicode[STIX]{x1D6FC}_{i}$
, dash-dotted line:
$\unicode[STIX]{x1D6FC}_{i}$
, dash-dotted line:
![]() $\unicode[STIX]{x1D706}_{z_{0}}=18.2$
(
$\unicode[STIX]{x1D706}_{z_{0}}=18.2$
(
![]() $\unicode[STIX]{x1D6FD}_{r_{0}}=0.68$
). (b) Streamwise growth rate and (c) amplification factor with respect to wave angle at several streamwise stations and
$\unicode[STIX]{x1D6FD}_{r_{0}}=0.68$
). (b) Streamwise growth rate and (c) amplification factor with respect to wave angle at several streamwise stations and
![]() $St_{0}$
. The arrows indicate the wave angle estimated from the experimentally observed wavelengths,
$St_{0}$
. The arrows indicate the wave angle estimated from the experimentally observed wavelengths,
![]() $\unicode[STIX]{x1D717}=27^{\circ }$
.
$\unicode[STIX]{x1D717}=27^{\circ }$
.
The stability of oblique disturbances in the boundary layer upstream of separation is assessed by examining the behaviour of the streamwise growth rate with respect to the wave angle,
![]() $\unicode[STIX]{x1D717}$
. The growth rates corresponding to the most unstable frequency are shown in figure 15(a) at several streamwise locations upstream of the critical point. As expected, all of the disturbances are damped upstream of the critical location. The same observations were made by Mack (Reference Mack1984) for a Blasius boundary layer (refer to their figure 6.6), albeit in that case oblique waves are unstable. Also agreeing with the findings in Mack (Reference Mack1984), is the variation of the growth rate of the oblique waves with frequency, shown in figure 15(b), at the critical streamwise location,
$\unicode[STIX]{x1D717}$
. The growth rates corresponding to the most unstable frequency are shown in figure 15(a) at several streamwise locations upstream of the critical point. As expected, all of the disturbances are damped upstream of the critical location. The same observations were made by Mack (Reference Mack1984) for a Blasius boundary layer (refer to their figure 6.6), albeit in that case oblique waves are unstable. Also agreeing with the findings in Mack (Reference Mack1984), is the variation of the growth rate of the oblique waves with frequency, shown in figure 15(b), at the critical streamwise location,
![]() $x_{c}$
. Figure 15(b) demonstrates that when two-dimensional disturbances begin to amplify, i.e. at
$x_{c}$
. Figure 15(b) demonstrates that when two-dimensional disturbances begin to amplify, i.e. at
![]() $x_{c}$
, oblique disturbances can be present, having growth rates comparable to or higher than those of the normal perturbations of the same frequency.
$x_{c}$
, oblique disturbances can be present, having growth rates comparable to or higher than those of the normal perturbations of the same frequency.

Figure 15. Streamwise growth rates with respect to wave angle,
![]() $\unicode[STIX]{x1D717}=\text{tan}^{-1}(\unicode[STIX]{x1D6FD}_{r}/\unicode[STIX]{x1D6FC}_{r})$
. (a) Selected streamwise positions at
$\unicode[STIX]{x1D717}=\text{tan}^{-1}(\unicode[STIX]{x1D6FD}_{r}/\unicode[STIX]{x1D6FC}_{r})$
. (a) Selected streamwise positions at
![]() $St_{0}=0.038$
(136 Hz) and (b) selected frequencies at
$St_{0}=0.038$
(136 Hz) and (b) selected frequencies at
![]() $x_{c}=-47$
. The arrows indicate the wave angle estimated from the experimentally observed wavelengths,
$x_{c}=-47$
. The arrows indicate the wave angle estimated from the experimentally observed wavelengths,
![]() $\unicode[STIX]{x1D717}=27^{\circ }$
.
$\unicode[STIX]{x1D717}=27^{\circ }$
.
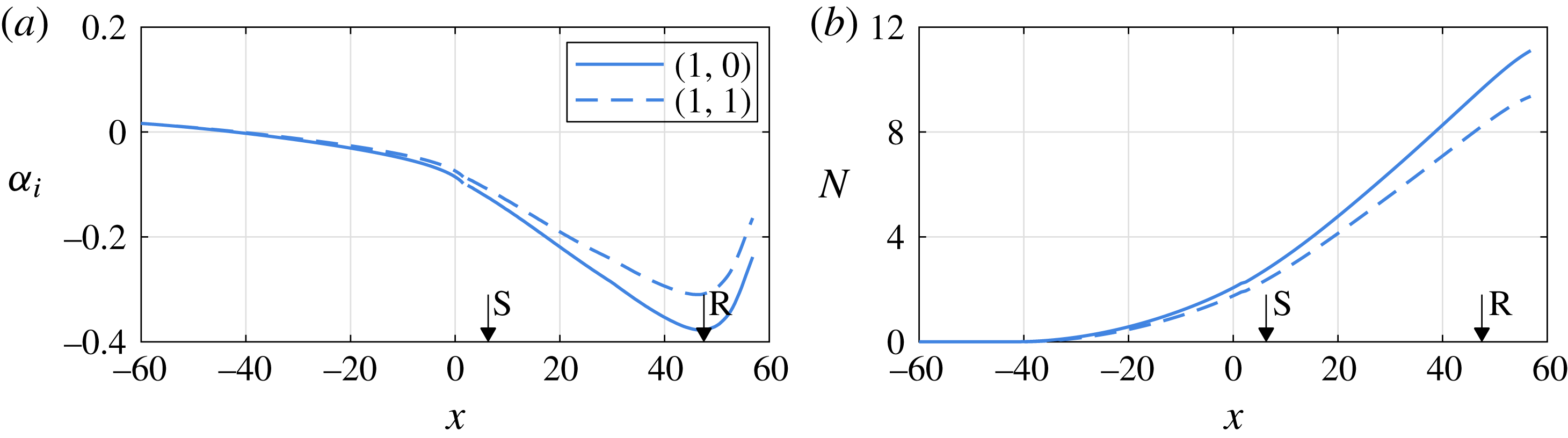
Figure 16. (a) Streamwise amplification rate and (b) amplification factor for the fundamental modes
![]() $(1,0)$
and
$(1,0)$
and
![]() $(1,1)$
, calculated on the composite flow field.
$(1,1)$
, calculated on the composite flow field.
It is instructive to compare the stability characteristics of the most amplified normal mode
![]() $(1,0)$
and that of the oblique mode
$(1,0)$
and that of the oblique mode
![]() $(1,1)$
associated with the same frequency and the spanwise wavenumber corresponding to the dominant spanwise wavelength observed in the experimental data (figure 9). Figures 16(a) and 16(b) compare the streamwise variation of the growth rates and amplification factors, respectively, for these two modes. As expected, both modes are amplified downstream of
$(1,1)$
associated with the same frequency and the spanwise wavenumber corresponding to the dominant spanwise wavelength observed in the experimental data (figure 9). Figures 16(a) and 16(b) compare the streamwise variation of the growth rates and amplification factors, respectively, for these two modes. As expected, both modes are amplified downstream of
![]() $x_{c}$
and experience comparable amplification rates up to the location of separation. The same observation has been made by Rist (Reference Rist1999) and Rist & Augustin (Reference Rist and Augustin2006) for oblique angles lower than
$x_{c}$
and experience comparable amplification rates up to the location of separation. The same observation has been made by Rist (Reference Rist1999) and Rist & Augustin (Reference Rist and Augustin2006) for oblique angles lower than
![]() $30^{\circ }$
. Once the separation point is approached, growth of disturbances is enhanced. While the normal mode
$30^{\circ }$
. Once the separation point is approached, growth of disturbances is enhanced. While the normal mode
![]() $(1,0)$
experiences stronger growth than the oblique mode, the latter demonstrates growth rates of the same order. In conjunction with the foregoing discussion, the implication here is that the oblique mode
$(1,0)$
experiences stronger growth than the oblique mode, the latter demonstrates growth rates of the same order. In conjunction with the foregoing discussion, the implication here is that the oblique mode
![]() $(1,1)$
can attain comparable magnitudes in the vicinity of the separation location, and its superposition with the more amplified normal mode can lead to vortex deformations observed in the present study (figure 7) and previous investigations (e.g. Nati et al.
Reference Nati, de Kat, Scarano and van Oudheusden2015; Kurelek et al.
Reference Kurelek, Lambert and Yarusevych2016).
$(1,1)$
can attain comparable magnitudes in the vicinity of the separation location, and its superposition with the more amplified normal mode can lead to vortex deformations observed in the present study (figure 7) and previous investigations (e.g. Nati et al.
Reference Nati, de Kat, Scarano and van Oudheusden2015; Kurelek et al.
Reference Kurelek, Lambert and Yarusevych2016).
4.3 Two-dimensional impulsive forcing
In view of the uncertainty regarding the formation of oblique modes, the boundary layer is impulsively forced in a two-dimensional manner by means of the plasma actuator described in § 2.3. The goal is to promote the normal mode
![]() $(1,0)$
via a controlled two-dimensional impulse. As a consequence, the normal mode is expected to reach much higher amplitudes in the LSB relative to unforced oblique modes, thereby diminishing the significance of the latter.
$(1,0)$
via a controlled two-dimensional impulse. As a consequence, the normal mode is expected to reach much higher amplitudes in the LSB relative to unforced oblique modes, thereby diminishing the significance of the latter.

Figure 17. Instantaneous
![]() $Q$
-criterion at several phases within a forcing cycle at an amplitude of
$Q$
-criterion at several phases within a forcing cycle at an amplitude of
![]() $C_{\unicode[STIX]{x1D707}}=1.6\times 10^{-4}$
. Grey, blue and red iso-surfaces correspond to
$C_{\unicode[STIX]{x1D707}}=1.6\times 10^{-4}$
. Grey, blue and red iso-surfaces correspond to
![]() $Q=0$
, 0.002 and 0.006 respectively. Arrows mark the main wave packet vortex associated with the forcing.
$Q=0$
, 0.002 and 0.006 respectively. Arrows mark the main wave packet vortex associated with the forcing.
Figure 17 depicts
![]() $Q$
-criterion values at several instants, for forcing amplitude of
$Q$
-criterion values at several instants, for forcing amplitude of
![]() $C_{\unicode[STIX]{x1D707}}=1.6\times 10^{-4}$
. An animated sequence of the flow development is provided as supplementary material (movie 2). At
$C_{\unicode[STIX]{x1D707}}=1.6\times 10^{-4}$
. An animated sequence of the flow development is provided as supplementary material (movie 2). At
![]() $\unicode[STIX]{x1D70F}=0$
, flow in the measurement volume is unperturbed, hence, strong spanwise deformation of the roll-up vortices is observed similar to the results shown in figure 7. The impulsively excited wave packet reaches the measurement volume in figure 17(b), and the evolution of the associated vortical structures is captured in figure 17(b–f). The vortex evolving directly from the impulse is marked by arrows in the images, and is followed by another strong induced structure, similar to the results of impulsive forcing reported by Michelis et al. (Reference Michelis, Kotsonis and Yarusevych2017). The streamwise wavelength of these vortices is consistent with that of the natural shedding and the linear stability predictions, which were confirmed by wavelet analysis at the centre of the volume. In contrast to the natural shedding, the rollers evolving from the impulse are strongly coherent along the span and experience minimal spanwise deformation within the measurement volume. Evidently, two-dimensional impulsive forcing is successful in suppressing spanwise deformations through the promotion of the normal instability mode
$\unicode[STIX]{x1D70F}=0$
, flow in the measurement volume is unperturbed, hence, strong spanwise deformation of the roll-up vortices is observed similar to the results shown in figure 7. The impulsively excited wave packet reaches the measurement volume in figure 17(b), and the evolution of the associated vortical structures is captured in figure 17(b–f). The vortex evolving directly from the impulse is marked by arrows in the images, and is followed by another strong induced structure, similar to the results of impulsive forcing reported by Michelis et al. (Reference Michelis, Kotsonis and Yarusevych2017). The streamwise wavelength of these vortices is consistent with that of the natural shedding and the linear stability predictions, which were confirmed by wavelet analysis at the centre of the volume. In contrast to the natural shedding, the rollers evolving from the impulse are strongly coherent along the span and experience minimal spanwise deformation within the measurement volume. Evidently, two-dimensional impulsive forcing is successful in suppressing spanwise deformations through the promotion of the normal instability mode
![]() $(1,0)$
, similar to the observations of Postl et al. (Reference Postl, Balzer and Fasel2011).
$(1,0)$
, similar to the observations of Postl et al. (Reference Postl, Balzer and Fasel2011).
Following the passage of the wave packet excited by the impulse over the reattachment region, the bubble undergoes a rapid contraction followed by bursting, as discussed in detail by Michelis et al. (Reference Michelis, Kotsonis and Yarusevych2017). Consequently, no clear evidence of shear layer roll up is seen in figure 17(g). As the bubble contracts back to its unperturbed state, weak spanwise structures re-emerge in figure 17(h), and quasi-steady natural shedding with pronounced spanwise deformations resumes (figure 17 i).
To determine the relative influence between normal and oblique modes under forcing, autocorrelation analysis is performed on the wall-normal velocity component extracted along the spanwise monitor line at the centre of the measurement volume (
![]() $x=48.5$
,
$x=48.5$
,
![]() $y=1.8$
, see figure 8). The resulting temporal variation of the normalised spanwise correlation coefficient prior to and after the introduction of the impulse
$y=1.8$
, see figure 8). The resulting temporal variation of the normalised spanwise correlation coefficient prior to and after the introduction of the impulse
![]() $(\unicode[STIX]{x1D70F}=0)$
is shown in figure 18. Evidently, for all time instants before the forced wave packet reaches the monitor line, the spanwise correlation coefficient exhibits negative peaks at
$(\unicode[STIX]{x1D70F}=0)$
is shown in figure 18. Evidently, for all time instants before the forced wave packet reaches the monitor line, the spanwise correlation coefficient exhibits negative peaks at
![]() $\unicode[STIX]{x0394}z\approx 18$
(i.e. structures of opposite shape), corresponding to the fundamental spanwise wavelength determined in the earlier analysis of the unforced bubble (figure 9). This is a direct outcome of the staggered spatial arrangement of the deformed rollers, which in turn is a result of linear interaction between normal and oblique modes in the boundary layer upstream of separation (see §§ 3.2 and 4.2). Similarly, weaker but positive correlation peaks at
$\unicode[STIX]{x0394}z\approx 18$
(i.e. structures of opposite shape), corresponding to the fundamental spanwise wavelength determined in the earlier analysis of the unforced bubble (figure 9). This is a direct outcome of the staggered spatial arrangement of the deformed rollers, which in turn is a result of linear interaction between normal and oblique modes in the boundary layer upstream of separation (see §§ 3.2 and 4.2). Similarly, weaker but positive correlation peaks at
![]() $\unicode[STIX]{x0394}z\approx 36$
indicate the existence of equal phase structures, forming the next group of rollers. When the wave packet generated by the impulse reaches the monitor line
$\unicode[STIX]{x0394}z\approx 36$
indicate the existence of equal phase structures, forming the next group of rollers. When the wave packet generated by the impulse reaches the monitor line
![]() $(\unicode[STIX]{x1D70F}\approx 3.5)$
, correlation coefficients reach uniform magnitudes across the span, approximately four times higher relatively to the unforced conditions. In line with the visualisation in figure 17, these outcomes point to a marked increase in the spanwise coherence of the shear layer vortices and diminishing of staggering, induced by the forcing of the normal mode
$(\unicode[STIX]{x1D70F}\approx 3.5)$
, correlation coefficients reach uniform magnitudes across the span, approximately four times higher relatively to the unforced conditions. In line with the visualisation in figure 17, these outcomes point to a marked increase in the spanwise coherence of the shear layer vortices and diminishing of staggering, induced by the forcing of the normal mode
![]() $(1,0)$
. It follows that once the bubble recedes, spanwise coherence diminishes until the bubble recovers, hence, the spanwise correlation coefficient is approximately zero between
$(1,0)$
. It follows that once the bubble recedes, spanwise coherence diminishes until the bubble recovers, hence, the spanwise correlation coefficient is approximately zero between
![]() $5<\unicode[STIX]{x1D70F}<13$
. Note that due to the staggered topology of the rollers, spanwise correlation coefficient peaks appear at twice the frequency of the shedding cycle.
$5<\unicode[STIX]{x1D70F}<13$
. Note that due to the staggered topology of the rollers, spanwise correlation coefficient peaks appear at twice the frequency of the shedding cycle.

Figure 18. Temporal variation of spanwise correlation coefficient based on autocorrelation of the wall-normal velocity component along the spanwise direction. The coefficients are normalised with the maximum value. Dashed line: lag matching the spanwise wavelength determined with wavelet analysis.
4.4 Mechanism of initial spanwise vortex deformations
The identified differences in the development of shear layer vortices in the aft portion of the bubble between natural and impulsively forced cases, combined with the results of the linear stability analysis, point to the following mechanism responsible for spanwise vortex deformations in LSBs. Linear stability theory analysis shows that normal and oblique modes of comparable growth rates can be present in the flow upstream of separation (figure 15), undergoing convective amplification downstream of the critical point (figure 16). The normal modes are the most amplified, their amplification at the fundamental frequency leading to the shear layer roll up and shedding seen in the aft portion of the bubble. However, a superposition of oblique and normal modes upstream of separation, would lead to spanwise undulations of the resulting perturbations that manifest in the observed spanwise deformations of vortices (figure 8). Note that such undulations in the boundary layer can also occur due to the interaction of two oblique modes alone (e.g. Berlin, Wiegel & Henningson Reference Berlin, Wiegel and Henningson1999; King & Breuer Reference King and Breuer2002), however, this is not deemed to be the case for the current study due to the presence of the normal mode (figure 12).

Figure 19. Waveforms of (a) mode
![]() $(1,0)$
, (b) mode
$(1,0)$
, (b) mode
![]() $(1,1)$
, (c) mode
$(1,1)$
, (c) mode
![]() $(1,-1)$
and their superposition in (d) natural and (e) forced conditions.
$(1,-1)$
and their superposition in (d) natural and (e) forced conditions.
A simplified model of superposition of the fundamental normal mode
![]() $(1,0)$
with the oblique mode
$(1,0)$
with the oblique mode
![]() $(1,1)$
and its mirrored counterpart
$(1,1)$
and its mirrored counterpart
![]() $(1,-1)$
is considered in figure 19. These modes are labelled as
$(1,-1)$
is considered in figure 19. These modes are labelled as
![]() $n$
,
$n$
,
![]() $b_{1}$
and
$b_{1}$
and
![]() $b_{2}$
in figure 19(a–c), respectively. It should be noted that the occurrence of the oblique mode
$b_{2}$
in figure 19(a–c), respectively. It should be noted that the occurrence of the oblique mode
![]() $(1,1)$
will be accompanied by its mirrored counterpart in a two-dimensional flow (Mack Reference Mack1984). For simplicity, the modes are modelled as sinusoidal waves whose salient characteristics are determined based on the analysis of experimental data and stability calculations. First, the superposition of these waves is considered for the unforced flow, namely, in the naturally developing LSB. For a given mode, the amplitude at a given streamwise location is given by
$(1,1)$
will be accompanied by its mirrored counterpart in a two-dimensional flow (Mack Reference Mack1984). For simplicity, the modes are modelled as sinusoidal waves whose salient characteristics are determined based on the analysis of experimental data and stability calculations. First, the superposition of these waves is considered for the unforced flow, namely, in the naturally developing LSB. For a given mode, the amplitude at a given streamwise location is given by
![]() $A=A_{0}e^{N}$
, where
$A=A_{0}e^{N}$
, where
![]() $A_{0}$
is the initial amplitude,
$A_{0}$
is the initial amplitude,
![]() $A_{0}=A(x_{c})$
, and
$A_{0}=A(x_{c})$
, and
![]() $N$
is the amplification factor. Assuming that the initial amplitudes of the normal and oblique waves are comparable, the ratio of their amplitudes at a given streamwise location is given by
$N$
is the amplification factor. Assuming that the initial amplitudes of the normal and oblique waves are comparable, the ratio of their amplitudes at a given streamwise location is given by
where the subscripts
![]() $n$
and
$n$
and
![]() $b$
identify the normal and oblique modes, respectively. For the oblique angle that matches the average ratio of streamwise and spanwise wavelengths determined experimentally (
$b$
identify the normal and oblique modes, respectively. For the oblique angle that matches the average ratio of streamwise and spanwise wavelengths determined experimentally (
![]() $\unicode[STIX]{x1D717}=27^{\circ }$
, figure 9), the corresponding
$\unicode[STIX]{x1D717}=27^{\circ }$
, figure 9), the corresponding
![]() $N$
factors can be obtained from figure 16. At
$N$
factors can be obtained from figure 16. At
![]() $x=40$
, located within the tomographic field of view, figure 16 gives
$x=40$
, located within the tomographic field of view, figure 16 gives
![]() $N_{n}=8.3$
and
$N_{n}=8.3$
and
![]() $N_{b}=7.1$
, leading to an amplitude ratio between normal and oblique waves of
$N_{b}=7.1$
, leading to an amplitude ratio between normal and oblique waves of
![]() $C_{nat}=A_{n}/A_{b}=3.3$
. The superposition of the normal and oblique modes with this amplitude ratio is depicted in figure 19(d). The results show distinct spanwise deformations similar to those observed in the vortex filaments developing in the natural bubble (figure 7). It should be emphasised that similar results can be obtained using oblique modes associated with other obliqueness angles, with the most amplified modes corresponding to oblique angles below
$C_{nat}=A_{n}/A_{b}=3.3$
. The superposition of the normal and oblique modes with this amplitude ratio is depicted in figure 19(d). The results show distinct spanwise deformations similar to those observed in the vortex filaments developing in the natural bubble (figure 7). It should be emphasised that similar results can be obtained using oblique modes associated with other obliqueness angles, with the most amplified modes corresponding to oblique angles below
![]() $30^{\circ }$
(figure 14
a), and that variations in the relative phase between the modes can change the position of the spanwise crests and valleys.
$30^{\circ }$
(figure 14
a), and that variations in the relative phase between the modes can change the position of the spanwise crests and valleys.
A similar superposition can be carried out for the case of an impulsively forced wave packet since flow stability characteristics do not change appreciably until the induced perturbations reach the mean reattachment location (Michelis et al. Reference Michelis, Kotsonis and Yarusevych2017). Here, the impulse effectively changes the initial amplitude of the normal mode, significantly increasing its amplitude within the LSB relative to that of the oblique modes. The amplitude of perturbations in the forced and unforced cases can be represented by (4.3) and (4.4), respectively,
where the forced and natural conditions are defined by the subscripts
![]() $f$
and
$f$
and
![]() $nat$
, respectively. Equation (4.3) assumes that the development of oblique waves is not affected substantially by the actuator due to its two-dimensional geometry. The amplitude ratio for the forced normal and oblique waves,
$nat$
, respectively. Equation (4.3) assumes that the development of oblique waves is not affected substantially by the actuator due to its two-dimensional geometry. The amplitude ratio for the forced normal and oblique waves,
![]() $C_{f}=A_{n_{f}}/A_{b}$
, can be obtained by taking the ratio of (4.3) and (4.4), and then utilising (4.2), leading to
$C_{f}=A_{n_{f}}/A_{b}$
, can be obtained by taking the ratio of (4.3) and (4.4), and then utilising (4.2), leading to
The ratio
![]() $A_{f}/A_{nat}$
can be estimated from measured velocity fluctuations, which gives
$A_{f}/A_{nat}$
can be estimated from measured velocity fluctuations, which gives
![]() $A_{f}/A_{nat}\approx 10$
at
$A_{f}/A_{nat}\approx 10$
at
![]() $x=40$
. Substituting this value and the amplification factors corresponding to the same streamwise location, gives
$x=40$
. Substituting this value and the amplification factors corresponding to the same streamwise location, gives
![]() $C_{f}=A_{n_{f}}/A_{b}\approx 40$
. The superposition of the normal and oblique modes with this amplitude ratio is illustrated in figure 19(e). The results demonstrate minimal spanwise deformations similar to what is observed in the forced vortical structures (figure 17).
$C_{f}=A_{n_{f}}/A_{b}\approx 40$
. The superposition of the normal and oblique modes with this amplitude ratio is illustrated in figure 19(e). The results demonstrate minimal spanwise deformations similar to what is observed in the forced vortical structures (figure 17).
The presented model agrees with the experimental observations and serves to confirm the proposed relation between vortex deformations and the amplification of oblique perturbations in the fore portion of the separation bubble. Evidently, in naturally developing LSBs, multiple oblique modes will be present, and their superposition with the fundamental normal mode will produce more complex deformations of the vortex filaments within a range of spanwise wavenumbers. Indeed, the statistical analysis of the experimental data (figures 4 and 9) shows that spanwise deformations are associated with a range of wavenumbers for a given vortex filament and also vary from cycle to cycle. While a range of unstable modes can be predicted by linear stability theory, the selection of the appearing structures is governed by a complex receptivity process. As such, the characteristics of the dominant oblique waves will vary for different experimental facilities due to the inevitable minor imperfections in model geometry and the content of the free-stream perturbations. Nonetheless, the results of the present study show that oblique modes are unstable upstream of the shear layer roll-up location and a presence of one or multiple oblique modes will result in spanwise undulations in the dominant shear layer rollers, which has been shown to be a precursor to vortex breakdown in the aft portion of the bubble (Marxen et al.
Reference Marxen, Lang and Rist2013; Kurelek et al.
Reference Kurelek, Lambert and Yarusevych2016). Along these lines, the direct numerical simulations of Rist & Maucher (Reference Rist and Maucher1994) in a similar bubble
![]() $(Re_{\unicode[STIX]{x1D6FF}_{s}^{\ast }}=1265,u_{rev}<0.03U_{\infty })$
, indicate that transition is primarily influenced by oblique modes rather than secondary instabilities. It should be emphasised that a superposition of normal and oblique modes occurs upstream of separation and possibly in the fore part of the LSB and serves as an initial spanwise perturbation of the vortices at roll up, with the subsequent development of spanwise vortex deformations governed by complex vortex dynamics, falling well beyond the purview of linear stability theory. Furthermore, the development of vortices in the aft portion of the bubble involves other, more complex instabilities responsible for vortex splitting and merging (figure 7) and the eventual vortex breakdown (Marxen et al.
Reference Marxen, Lang and Rist2013).
$(Re_{\unicode[STIX]{x1D6FF}_{s}^{\ast }}=1265,u_{rev}<0.03U_{\infty })$
, indicate that transition is primarily influenced by oblique modes rather than secondary instabilities. It should be emphasised that a superposition of normal and oblique modes occurs upstream of separation and possibly in the fore part of the LSB and serves as an initial spanwise perturbation of the vortices at roll up, with the subsequent development of spanwise vortex deformations governed by complex vortex dynamics, falling well beyond the purview of linear stability theory. Furthermore, the development of vortices in the aft portion of the bubble involves other, more complex instabilities responsible for vortex splitting and merging (figure 7) and the eventual vortex breakdown (Marxen et al.
Reference Marxen, Lang and Rist2013).
The current findings shed light on the underlying physics responsible for the differences in the development of roll-up vortices seen in different previous studies. For example, for an LSB on a NACA 0018 aerofoil, progressive development of spanwise deformations within a range of spanwise wavenumbers was recently reported by Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016) (see their figures 14 and 15), who propose a model linking local vortex breakdown to the development of crests in vortex filaments. Similar progressive spanwise vortex deformations have been observed by Nati et al. (Reference Nati, de Kat, Scarano and van Oudheusden2015) on an SD 7003 aerofoil. The results of Burgmann & Schröder (Reference Burgmann and Schröder2008) and Hain et al. (Reference Hain, Kähler and Radespiel2009) show a more pronounced onset of vortex deformations on an SD 7003 profile at comparable Reynolds numbers (see their figures 16 and 25, respectively). The observed differences are attributed to the different relative magnitudes of the dominant normal and oblique modes in the respective studies, which, as discussed earlier, are dependent on both the stability characteristics and specific experimental environment. This is further substantiated by the direct numerical simulations of Jones et al. (Reference Jones, Sandbergh and Sandham2008). They observe strongly deformed roll up in the LSB subjected to three-dimensional forcing (see their figure 11a), i.e. when both normal and oblique modes are promoted, while spanwise coherent vortices form when such forcing is removed (see their figure 11b). Thus, similar to the results of the proposed model (figure 19), the degree of the spanwise deformation of the rollers is related to the relative strength of the fundamental normal and oblique instability modes in a given flow scenario. Furthermore, this provides an explanation for the observed delay in vortex breakdown in recent studies where the development of the normal mode was promoted via two-dimensional forcing (e.g. Michelis et al. Reference Michelis, Kotsonis and Yarusevych2017; Yarusevych & Kotsonis Reference Yarusevych and Kotsonis2017a ).
Finally, it has to be emphasised that the discussed model is applicable in flow scenarios with relatively low levels of free-stream turbulence and surface roughness. At higher levels of free-stream or localised perturbations, pronounced streamwise structures can develop in the attached boundary layer (Brinkerhoff & Yaras Reference Brinkerhoff and Yaras2011; Rao et al.
Reference Rao, Jefferson-Loveday, Tucker and Lardeau2014; Brinkerhoff & Yaras Reference Brinkerhoff and Yaras2015) and, in the extreme cases, bypass transition can be triggered (Jacobs & Durbin Reference Jacobs and Durbin2001). In addition, the investigated bubble is characterised by mild reverse flow velocities, so that the transition process is dominated by the interaction of convective disturbances. For stronger reverse flow conditions
![]() $(\gtrapprox 7\,\%)$
, absolute/global instability considerations are warranted.
$(\gtrapprox 7\,\%)$
, absolute/global instability considerations are warranted.
5 Summary and concluding remarks
An experimental investigation is carried out in order to investigate three-dimensional, spatio-temporal flow development in a laminar separation bubble and to elucidate its relation to flow stability. A separation bubble is formed on the flat plate subjected to an adverse pressure gradient. The LSB features reverse flow of approximately 2 % of the local free-stream velocity, where the bubble dynamics is driven primarily by convective instabilities. Time-resolved velocity measurements are performed by means of planar and tomographic particle image velocimetry. The measurements are complemented with a numerical solution of the boundary layer equations, which allows for a joint analysis of the flow in the attached and separated flow regions. The stability characteristics of the combined flow field are assessed by means of linear stability theory. In addition to the natural evolution of the flow within a laminar separation bubble, deterministic, two-dimensional, impulsive forcing via a DBD plasma actuator is employed to assess the effect of forcing the normal instability mode on the bubble dynamics. The results show that a strong amplification of disturbances in the LSB leads to shear layer roll up and shedding of spanwise oriented vortices in the aft portion of the bubble. However, these structures are shown to develop distinct spanwise deformations followed by complex vortex interactions, involving vortex splitting, merging and the development of weaker streamwise vortex connections. Wavelet analysis in spatial formulation demonstrates that the spanwise deformations for a given vortex involve a range of wavelengths, with a statistical mean streamwise to spanwise wavelength ratio of approximately 1 : 2.
In order to elucidate the mechanism pertinent to the incipient spanwise deformations of the vortices in the LSB, linear stability theory analysis is performed. The results demonstrate that the flow becomes unstable in the adverse pressure region upstream of separation. Upstream of the critical point, oblique modes are less damped compared to the normal modes. However, downstream of the critical point, the normal mode is the most amplified, while the predicted frequency of the most amplified disturbances matches that of the vortex shedding frequency, linking the shear layer roll up to the amplification of the normal fundamental mode. At the same time, oblique instabilities are also shown to amplify substantially downstream of the critical point, with the highest amplification rates associated with oblique angles below approximately
![]() $30^{\circ }$
. Moreover, within this range of oblique angles, the growth rate of oblique modes remains virtually invariant to frequency, with the largest growth associated with the fundamental frequency of the most amplified normal mode. Thus, both normal and oblique waves are amplified in the fore portion of the separation bubble, and their superposition would produce spanwise undulation in the shed vortices, with the degree of such initial undulation being dependent on the relative amplitude of the dominant normal and oblique modes. This is further reaffirmed by the outcomes of frequency–wavelength spectra within the tomographic PIV domain, elucidating the existence of both oblique and normal modes.
$30^{\circ }$
. Moreover, within this range of oblique angles, the growth rate of oblique modes remains virtually invariant to frequency, with the largest growth associated with the fundamental frequency of the most amplified normal mode. Thus, both normal and oblique waves are amplified in the fore portion of the separation bubble, and their superposition would produce spanwise undulation in the shed vortices, with the degree of such initial undulation being dependent on the relative amplitude of the dominant normal and oblique modes. This is further reaffirmed by the outcomes of frequency–wavelength spectra within the tomographic PIV domain, elucidating the existence of both oblique and normal modes.
Impulsive, two-dimensional forcing results in the emergence of a convectively unstable wave packet whose frequency is determined through selective amplification and matches the fundamental frequency of the unforced case. The results demonstrate that the vortical structures produced by the impulsive perturbation feature strong spanwise coherence, significantly differing from the vortices produced in the naturally developing flow. This is attributed to the promotion of the normal mode through two-dimensional forcing. A simplified linear superposition model is presented to illustrate that the observed differences in vortex topology are attributed to the superposition of normal and oblique instability modes of different amplitude. Utilising the linear stability calculations and measurements, it is shown that a superposition of the fundamental normal and oblique waves of comparable magnitudes leads to substantial spanwise deformations of the most amplified perturbations in the natural separation bubble. In contrast, when two-dimensional forcing is engaged, the relative amplitude of the normal mode is increased by an order of magnitude, leading to a significant increase in the spanwise uniformity of the vortices at formation.
The present study demonstrates that, for an LSB with mild reverse flow magnitude (
![]() ${\approx}2\,\%$
of the local free-stream velocity) the initial spanwise perturbations of the dominant vortical structures at formation is driven by the superposition of the normal and oblique modes amplified well upstream of separation, and the initial amplitude of such a deformation is dictated by the relative amplitude of the modes. Similar ‘oblique breakdown’ of primary shear layer vortices has been recently observed in numerical simulations where oblique modes were forced artificially (Marxen Reference Marxen2017). While deviations are expected based on specific flow conditions, it appears that such a scenario for the late stages of transition is favoured in the case of mild reverse flow magnitudes (up to 2 % for this study) and a relatively shallow angle of the oblique mode pair.
${\approx}2\,\%$
of the local free-stream velocity) the initial spanwise perturbations of the dominant vortical structures at formation is driven by the superposition of the normal and oblique modes amplified well upstream of separation, and the initial amplitude of such a deformation is dictated by the relative amplitude of the modes. Similar ‘oblique breakdown’ of primary shear layer vortices has been recently observed in numerical simulations where oblique modes were forced artificially (Marxen Reference Marxen2017). While deviations are expected based on specific flow conditions, it appears that such a scenario for the late stages of transition is favoured in the case of mild reverse flow magnitudes (up to 2 % for this study) and a relatively shallow angle of the oblique mode pair.
Further development of the perturbed vortex filaments is governed by the attendant vortex dynamics, leading to complex vortex interactions and the eventual breakdown of the structures. In practice, the initial amplitude of spanwise perturbations will vary based on the receptivity and stability conditions for a given flow, as well as the nature of the experimental conditions such as free-stream environment and geometric imperfections. This explains the differences in vortex dynamics observed in relevant studies (Burgmann et al. Reference Burgmann, Dannemann and Schröder2008; Nati et al. Reference Nati, de Kat, Scarano and van Oudheusden2015). In particular, while distinct deformations of vortex filaments were observed, their severity varied significantly between the studies due to the aforementioned considerations, thereby affecting substantially the flow dynamics in the aft part of the bubble and, hence, the overall flow topology. The current results also show that the promotion of the fundamental normal mode can serve to reduce significantly the spanwise deformation of the shear layer vortices, thereby delaying vortex breakdown, as seen in Postl et al. (Reference Postl, Balzer and Fasel2011) and Michelis et al. (Reference Michelis, Kotsonis and Yarusevych2017). Alternatively, oblique forcing can be used to reduce the spanwise coherence of vortices at roll-up and accelerate their decay, which is of interest, for example, for the control of trailing edge tonal noise produced by these structures (e.g. Pröbsting & Yarusevych Reference Pröbsting and Yarusevych2015).
Acknowledgement
The authors would like to thank Dr O. Marxen, University of Surrey, for the valuable discussions that led to the improvement of this manuscript.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2018.91.