Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T23:17:08.620Z Has data issue: false hasContentIssue false
  • English
  • Français

On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier–Stokes models

Published online by Cambridge University Press:  23 August 2018

Bjarke Eltard Larsen Open the ORCID record for Bjarke Eltard Larsen [Opens in a new window]  and
David R. Fuhrman
Bjarke Eltard Larsen*
Affiliation:
Technical University of Denmark, Department of Mechanical Engineering, Section of Fluid Mechanics, Coastal and Maritime Engineering, DK-2800 Kgs. Lyngby, Denmark
David R. Fuhrman
Affiliation:
Technical University of Denmark, Department of Mechanical Engineering, Section of Fluid Mechanics, Coastal and Maritime Engineering, DK-2800 Kgs. Lyngby, Denmark
*
†Email address for correspondence: bjelt@mek.dtu.dk
Get access Rights & Permissions [Opens in a new window]

Abstract

In previous computational fluid dynamics studies of breaking waves, there has been a marked tendency to severely over-estimate turbulence levels, both pre- and post-breaking. This problem is most likely related to the previously described (though not sufficiently well recognized) conditional instability of widely used turbulence models when used to close Reynolds-averaged Navier–Stokes (RANS) equations in regions of nearly potential flow with finite strain, resulting in exponential growth of the turbulent kinetic energy and eddy viscosity. While this problem has been known for nearly 20 years, a suitable and fundamentally sound solution has yet to be developed. In this work it is demonstrated that virtually all commonly used two-equation turbulence closure models are unconditionally, rather than conditionally, unstable in such regions. A new formulation of the 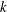$k$–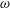$\unicode[STIX]{x1D714}$ closure is developed which elegantly stabilizes the model in nearly potential flow regions, with modifications remaining passive in sheared flow regions, thus solving this long-standing problem. Computed results involving non-breaking waves demonstrate that the new stabilized closure enables nearly constant form wave propagation over long durations, avoiding the exponential growth of the eddy viscosity and inevitable wave decay exhibited by standard closures. Additional applications on breaking waves demonstrate that the new stabilized model avoids the unphysical generation of pre-breaking turbulence which widely plagues existing closures. The new model is demonstrated to be capable of predicting accurate pre- and post-breaking surface elevations, as well as turbulence and undertow velocity profiles, especially during transition from pre-breaking to the outer surf zone. Results in the inner surf zone are similar to standard closures. 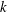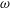Similar methods for formally stabilizing other widely used closure models ($k$–$\unicode[STIX]{x1D714}$ and $k$–$\unicode[STIX]{x1D700}$ variants) are likewise developed, and it is recommended that these be utilized in future RANS simulations of surface waves. (In the above 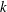$k$ is the turbulent kinetic energy density, 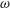$\unicode[STIX]{x1D714}$ is the specific dissipation rate, and $\unicode[STIX]{x1D700}$ is the dissipation.)

JFM classification

Waves/Free-surface Flows: Surface gravity waves Turbulent Flows: Turbulence modelling Waves/Free-surface Flows: Wave breaking
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 419 - 460
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van der A, D. A., van der Zanden, J., O’Donoghue, T., Hurther, D., Caceres, I., McLelland, S. J. & Ribberink, J. S. 2017 Large-scale laboratory study of breaking wave hydrodynamics over a fixed bar. J. Geophys. Res. 122 (4), 3287–3310.Google Scholar
Baykal, C., Sumer, B. M., Fuhrman, D. R., Jacobsen, N. G. & Fredsøe, J. 2015 Numerical investigation of flow and scour around a vertical circular cylinder. Phil. Trans. R. Soc. A 373, 20140104.Google Scholar
Bayraktar, D., Ahmad, J., Larsen, B. E., Carstensen, S. & Fuhrman, D. R. 2016 Experimental and numerical study of wave-induced backfilling beneath submarine pipelines. Coast. Engng 118, 63–75.Google Scholar
Belden, J. & Techet, A. H. 2011 Simultaneous quantitative flow measurement using PIV on both sides of the air–water interface for breaking waves. Exp. Fluids 50 (1), 149–161.Google Scholar
Berberovic, E., van Hinsberg, N. P., Jakirlic, S., Roisman, I. V. & Tropea, C. 2009 Drop impact onto a liquid layer of finite thickness: dynamics of the cavity evolution. Phys. Rev. E 79 (3), 036306.Google Scholar
Bradford, S. F. 2000 Numerical simulation of surf zone dynamics. ASCE J. Waterway Port Coastal Ocean Engng 126 (1), 1–13.Google Scholar
Bradford, S. F. 2011 Nonhydrostatic model for surf zone simulation. ASCE J. Waterway Port Coastal Ocean Engng 137 (4), 163–174.Google Scholar
Brown, S. A., Greaves, D. M., Magar, V. & Conley, D. C. 2016 Evaluation of turbulence closure models under spilling and plunging breakers in the surf zone. Coast. Engng 114, 177–193.Google Scholar
Burchard, H. 2002 Applied Turbulence Modelling for Marine Waters. Springer.Google Scholar
Cebeci, T. & Chang, K. C. 1978 Calculation of incompressible rough-wall boundary-layer flows. AIAA J. 16, 730–735.Google Scholar
Chang, K. A. & Liu, P. L. F. 1998 Velocity, acceleration and vorticity under a breaking wave. Phys. Fluids 10 (1), 327–329.Google Scholar
Chen, L. F., Zang, J., Hillis, A. J., Morgan, G. C. J. & Plummer, A. R. 2014 Numerical investigation of wave-structure interaction using OpenFOAM. Ocean Engng 88, 91–109.Google Scholar
Christensen, E. D. 2006 Large eddy simulation of spilling and plunging breakers. Coast. Engng 53 (5–6), 463–485.Google Scholar
Deshpande, S. S., Anumolu, L. & Trujillo, M. F. 2012 Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Disc. 5 (1), 014016.Google Scholar
Devolder, B., Rauwoens, P. & Troch, P. 2017 Application of a buoyancy-modified k–𝜔 SST turbulence model to simulate wave run-up around a monopile subjected to regular waves using OpenFOAM (R). Coast. Engng 125, 81–94.Google Scholar
Duncan, J. H., Qiao, H. B., Philomin, V. & Wenz, A. 1999 Gentle spilling breakers: crest profile evolution. J. Fluid Mech. 379, 191–222.Google Scholar
Durbin, P. A. 2009 Limiters and wall treatments in applied turbulence modeling. Fluid Dyn. Res. 41 (1), 012203.Google Scholar
Fenton, J. D. 1988 The numerical solution of steady water wave problems. Comput. Geosci. 14, 357–368.Google Scholar
Fuhrman, D. R., Baykal, C., Sumer, B. M., Jacobsen, N. G. & Fredsoe, J. 2014 Numerical simulation of wave-induced scour and backfilling processes beneath submarine pipelines. Coast. Engng 94, 10–22.Google Scholar
Fuhrman, D. R., Schløer, S. & Sterner, J. 2013 RANS-based simulation of turbulent wave boundary layer and sheet-flow sediment transport processes. Coast. Engng 73, 151–166.Google Scholar
Grue, J. & Jensen, A. 2006 Experimental velocities and accelerations in very steep wave events in deep water. Eur. J. Mech. (B/Fluids) 25 (5), 554–564.Google Scholar
Harlow, F. H. & Welch, J. E. 1965 Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 8 (12), 2182–2189.Google Scholar
Hieu, P. D., Katsutohi, T. & Ca, V. T. 2004 Numerical simulation of breaking waves using a two-phase flow model. Appl. Math. Model. 28 (11), 983–1005.Google Scholar
Higuera, P., Lara, J. L. & Losada, I. J. 2013 Simulating coastal engineering processes with OpenFOAM (R). Coast. Engng 71, 119–134.Google Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid VOF method for the dynamics of free boundaries. J. Comput. Phys. 39 (1), 201–225.Google Scholar
Hsu, T., Hsieh, C., Tsai, C. & Ou, S. 2015 Coupling VOD/PLIC and embedding method for simulating wave breaking on a sloping beach. J. Mar. Sci. Technol. 23 (4), 498–507.Google Scholar
Hsu, T. J., Sakakiyama, T. & Liu, P. L. F. 2002 A numerical model for wave motions and turbulence flows in front of a composite breakwater. Coast. Engng 46 (1), 25–50.Google Scholar
Hu, Z. Z., Greaves, D. & Raby, A. 2016 Numerical wave tank study of extreme waves and wave-structure interaction using OpenFoam (R). Ocean Engng 126, 329–342.Google Scholar
Jacobsen, N. G., Fredsøe, J. & Jensen, J. H. 2014 Formation and development of a breaker bar under regular waves. Part 1. Model description and hydrodynamics. Coast. Engng 88, 182–193.Google Scholar
Jacobsen, N. G., Fuhrman, D. R. & Fredsøe, J. 2012 A wave generation toolbox for the open-source CFD library: OpenFOAM (R). Intl J. Numer. Meth. Fluids 70, 1073–1088.Google Scholar
Jacobsen, N. G., van Gent, M. R. A. & Wolters, G. 2015 Numerical analysis of the interaction of irregular waves with two dimensional permeable coastal structures. Coast. Engng 102, 13–29.Google Scholar
Kimmoun, O. & Branger, H. 2007 A particle image velocimetry investigation on laboratory surf-zone breaking waves over a sloping beach. J. Fluid Mech. 588, 353–397.Google Scholar
Larsen, B. E.2018 Tsunami-seabed interactions. PhD thesis, Technical University of Denmark, Denmark.Google Scholar
Larsen, B. E., Arbøll, L. K., Frigaard, S., Carstensen, S. & Fuhrman, D. R. 2018a Experimental study of tsunami-induced scour around a monopile foundation. Coast. Engng 138, 9–21.Google Scholar
Larsen, B. E., Fuhrman, D. R., Baykal, C. & Sumer, B. M. 2017 Tsunami-induced scour around monopile foundations. Coast. Engng 129, 36–49.Google Scholar
Larsen, B. E., Fuhrman, D. R. & Roenby, J.2018b Performance of interFoam on the simulation of progressive waves. arXiv:1804.01158 [physics.flu-dyn].Google Scholar
Larsen, B. E., Fuhrman, D. R. & Sumer, B. M. 2016 Simulation of wave-plus-current scour beneath submarine pipelines. ASCE J. Waterway Port Coastal Ocean Engng 142 (5), 08216001.Google Scholar
Launder, B. E. & Sharma, B. I. 1974 Application of the energy-dissipation model or turbulence to the calculation of flow near a spinning disc. Lett. Heat Mass Transfer 1 (2), 131–137.Google Scholar
Lemos, C. M. 1992 Wave breaking: a numerical study. In Lecture Notes in Engineering, vol. 71, pp. 1–185. Springer.Google Scholar
Lin, P. Z. & Liu, P. L. F. 1998 A numerical study of breaking waves in the surf zone. J. Fluid Mech. 359, 239–264.Google Scholar
Makris, C. V., Memos, C. D. & Krestenitis, Y. N. 2016 Numerical modeling of surf zone dynamics under weakly plunging breakers with SPH method. Ocean Model. 98, 12–35.Google Scholar
Mayer, S. & Madsen, P. A. 2000 Simulations of breaking waves in the surf zone using a Navier–Stokes solver. In Proc. 25th Intl Conf. Coast. Engng, pp. 928–941. ASCE.Google Scholar
Menter, F. R. 1994 Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32 (8), 1598–1605.Google Scholar
Paulsen, B. T., Bredmose, H., Bingham, H. B. & Jacobsen, N. G. 2014 Forcing of a bottom-mounted circular cylinder by steep regular water waves at finite depth. J. Fluid Mech. 755, 1–34.Google Scholar
Rodi, W. 1987 Examples of calculation methods for flow and mixing in stratified fluids. J. Geophys. Res. 92 (C5), 5305–5328.Google Scholar
Roenby, J., Larsen, B. E., Bredmose, H. & Jasak, H. 2017 A new volume-of-fluid method in OpenFOAM. In 7th Intl Conf. Comput. Methods Marine Engng, pp. 1–12. International Centre for Numerical Methods in Engineering.Google Scholar
Ruessink, B. G., van den Berg, T. J. J. & van Rijn, L. C. 2009 Modeling sediment transport beneath skewed asymmetric waves above a plane bed. J. Geophys. Res. 114, C11021.Google Scholar
Sakai, T., Mizutani, T., Tanaka, H. & Tada, Y. 1986 Vortex formation in plunging breakers. In Proc. 20th Conf. Coast. Engng, pp. 711–723. ASCE.Google Scholar
Schmitt, P. & Elsaesser, B. 2015 On the use of OpenFOAM to model oscillating wave surge converters. Ocean Engng 108, 98–104.Google Scholar
Schumann, U. & Gerz, T. 1995 Turbulent mixing in stably stratified shear flows. J. Appl. Meteorol. 34 (1), 33–48.Google Scholar
Scott, C. P., Cox, D. T., Maddux, T. B. & Long, J. W. 2005 Large-scale laboratory observations of turbulence on a fixed barred beach. Meas. Sci. Technol. 16 (10), 1903–1912.Google Scholar
Shao, S. 2006 Simulation of breaking wave by SPH method coupled with k–𝜖 model. J. Hydraul. Res. 44 (3), 338–349.Google Scholar
Stive, M. J. F. & Wind, H. G. 1982 A study of radiation stress and set-up in the nearshore region. Coast. Engng 6 (1), 1–25.Google Scholar
Svendsen, I. A. 1987 Analysis of surf zone turbulence. J. Geophys. Res. 92 (C5), 5115–5124.Google Scholar
Ting, F. C. K. & Kirby, J. T. 1994 Observation of undertow and turbulence in a laboratory surf zone. Coast. Engng 24 (1–2), 51–80.Google Scholar
Ting, F. C. K. & Kirby, J. T. 1996 Dynamics of surf-zone turbulence in a spilling breaker. Coast. Engng 27 (3–4), 131–160.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Umlauf, L., Burchard, H. & Hutter, K. 2003 Extending the k–𝜔 turbulence model towards oceanic applications. Ocean Model. 5 (3), 195–218.Google Scholar
Watanabe, Y. & Saeki, H. 1999 Three-dimensional large eddy simulation of breaking waves. Coast. Engng J. 41 (3–4), 281–301.Google Scholar
Wilcox, D. C. 1988 Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 26 (11), 1299–1310.Google Scholar
Wilcox, D. C. 2006 Turbulence Modeling for CFD, 3rd edn. DCW Industries, Inc.Google Scholar
Wilcox, D. C. 2008 Formulation of the k–𝜔 turbulence model revisited. AIAA J. 46, 2823–2838.Google Scholar
Xie, Z. 2013 Two-phase flow modelling of spilling and plunging breaking waves. Appl. Math. Model. 37 (6), 3698–3713.Google Scholar
Yakhot, V., Thangam, S., Speziale, C. G., Orszag, S. A. & Gatski, T. B. 1991 Development of turbulence models for shear flows by a double expansion technique. Inst. Comput. Appl. Sci. Engng NAS1-18605, 91–65, 1–24.Google Scholar