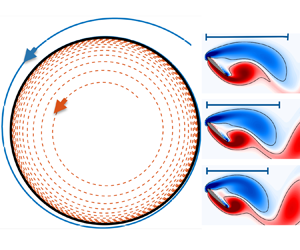
1. Introduction
Unsteady periodic fluid flows are common in nature and engineering settings, including vortex shedding over flapping wings, bluff bodies and airfoils. Modifying the vortex shedding behaviour of wake flows is of high relevance to developing efficient engineering systems. However, controlling such flows is challenging owing to their periodically varying base states (Colonius & Williams Reference Colonius and Williams2011). For the time-periodic base state, the timing of actuation becomes important. For this purpose, it is necessary to characterize the perturbation dynamics with respect to the time-periodic base state, which can be achieved using a phase reduction technique (Winfree Reference Winfree1967; Kuramoto Reference Kuramoto1984). The phase reduction approach expresses the perturbation dynamics using a single scalar phase variable. Recently, it has been used for studying periodic flows to reveal the phase sensitivity fields (Kawamura & Nakao Reference Kawamura and Nakao2013, Reference Kawamura and Nakao2015; Khodkar & Taira Reference Khodkar and Taira2020; Iima Reference Iima2021; Loe et al. Reference Loe, Nakao, Jimbo and Kotani2021; Kawamura, Godavarthi & Taira Reference Kawamura, Godavarthi and Taira2022), synchronization characteristics to external forcing (Taira & Nakao Reference Taira and Nakao2018; Khodkar & Taira Reference Khodkar and Taira2020; Khodkar, Klamo & Taira Reference Khodkar, Klamo and Taira2021; Skene & Taira Reference Skene and Taira2022) and flow control (Nair et al. Reference Nair, Taira, Brunton and Brunton2021; Loe et al. Reference Loe, Zheng, Kotani and Jimbo2023) in a computationally inexpensive way.
Examining synchronization properties for periodic wakes can offer insights to modify the vortex shedding behaviour and has several applications in unsteady flow control and fluid–structure interactions. Control of vortex shedding of wake flows has direct implications towards modifying the aerodynamic characteristics, reduction of structural vibration and noise emissions. Synchronization control has been studied in the context of vortex-induced vibrations for bluff-body wakes (Feng & Wang Reference Feng and Wang2010; Konstantinidis & Bouris Reference Konstantinidis and Bouris2016). In addition, actuating a flow by taking advantage of synchronization can be efficient in enhancing the aerodynamic performance (Pastoor et al. Reference Pastoor, Henning, Noack, King and Tadmor2008; Joe, Colonius & MacMynowski Reference Joe, Colonius and MacMynowski2011; Wang & Tang Reference Wang and Tang2018; Asztalos, Dawson & Williams Reference Asztalos, Dawson and Williams2021). Further, hydrodynamic synchronization is shown to result in efficient swimming in microscale swimmers at lower Reynolds number (Golestanian, Yeomans & Uchida Reference Golestanian, Yeomans and Uchida2011; Kawamura & Tsubaki Reference Kawamura and Tsubaki2018). Hence, it is beneficial to analyse the parameters that result in optimal synchronization in fluid flows. While most synchronization studies for fluid flows have characterized this asymptotic synchronization process to external sinusoidal actuation (Taira & Nakao Reference Taira and Nakao2018; Herrmann et al. Reference Herrmann, Oswald, Semaan and Brunton2020; Khodkar & Taira Reference Khodkar and Taira2020; Giannenas, Laizet & Rigas Reference Giannenas, Laizet and Rigas2022), it is often desirable to modify the vortex shedding as quickly as possible for flow control to take effect. This study considers the fast synchronization of wakes to an external forcing signal for wake flows.
The concept of fast synchronization has been studied in biology to promote the rapid adjustment of the biological clock to jet lag and facilitate treatments for cardiac arrhythmias (Guevara & Glass Reference Guevara and Glass1982; Granada & Herzel Reference Granada and Herzel2009). In the context of biological and simpler oscillatory systems, Zlotnik et al. (Reference Zlotnik, Chen, Kiss, Tanaka and Li2013) and Takata, Kato & Nakao (Reference Takata, Kato and Nakao2021) applied the phase reduction approach to analytically obtain the optimal waveform for fast synchronization, maximizing the synchronization speed to external periodic forcing. In dynamical systems, synchronization is also referred to as entrainment (Strogatz Reference Strogatz1994).
In this study, we apply such a phase reduction approach to perform the phase-based fast synchronization for NACA0012 airfoil wakes at post-stall angles of attack with leading- and trailing-edge actuation. The overview of the fast synchronization analysis is shown in figure 1. We analytically find the optimal actuation waveforms, and the airfoil wake flows are actuated numerically using the optimal and sinusoidal waveforms at various forcing frequencies. The respective synchronization speeds are compared to validate the theoretical results. Further, we investigate the influence of actuation on the flow fields and the lift coefficients. The paper is organized as follows. The phase-based description and the framework to obtain the waveform for fast synchronization are presented in § 2. The current approach is demonstrated with an example of NACA0012 airfoil wakes in § 3. Conclusions are offered in § 4.

Figure 1. Fast synchronization analysis of flow over a NACA0012 airfoil at ![]() $\alpha =55^\circ$ and
$\alpha =55^\circ$ and ![]() ${Re}=100$. (a) Periodic actuation using the optimal waveform. (b) Comparison of the synchronized flow field for a forcing frequency
${Re}=100$. (a) Periodic actuation using the optimal waveform. (b) Comparison of the synchronized flow field for a forcing frequency ![]() $\varOmega _f = 0.9\varOmega _n$ with the baseline vorticity field
$\varOmega _f = 0.9\varOmega _n$ with the baseline vorticity field ![]() $\boldsymbol {\omega }$. (c) Lift coefficient
$\boldsymbol {\omega }$. (c) Lift coefficient ![]() $C_L(t)$ when actuated with the fast synchronization and sinusoidal waveforms.
$C_L(t)$ when actuated with the fast synchronization and sinusoidal waveforms.
2. Fast synchronization analysis through the phase reduction approach
To obtain the optimal actuation waveform for fast synchronization for periodic fluid flows, we use phase reduction analysis (Taira & Nakao Reference Taira and Nakao2018; Kawamura et al. Reference Kawamura, Godavarthi and Taira2022). We identify the phase sensitivity fields that encode the effect of timing of actuation, and then analytically solve an optimization problem to obtain the synchronization waveform in terms of the phase sensitivity function.
2.1. Phase reduction approach
We consider incompressible time-periodic fluid flows governed by the Navier–Stokes equations ![]() $\dot {\boldsymbol {q}}= \mathcal {N}(\boldsymbol {q}(\boldsymbol {x},t))$, where
$\dot {\boldsymbol {q}}= \mathcal {N}(\boldsymbol {q}(\boldsymbol {x},t))$, where ![]() $\boldsymbol {q}$ is the flow state. These equations are given by
$\boldsymbol {q}$ is the flow state. These equations are given by
 \begin{equation} \left.\begin{gathered} \frac{\partial \boldsymbol{q}}{\partial t} ={-}\boldsymbol{q}\boldsymbol{\cdot}\boldsymbol{\nabla} \boldsymbol{q}-\boldsymbol{\nabla} p +\frac{1}{Re} \nabla^2 \boldsymbol{q}, \\ \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{q} =0, \end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered} \frac{\partial \boldsymbol{q}}{\partial t} ={-}\boldsymbol{q}\boldsymbol{\cdot}\boldsymbol{\nabla} \boldsymbol{q}-\boldsymbol{\nabla} p +\frac{1}{Re} \nabla^2 \boldsymbol{q}, \\ \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{q} =0, \end{gathered}\right\}\end{equation}
where ![]() ${Re}$ is the Reynolds number and
${Re}$ is the Reynolds number and ![]() $p$ is the pressure. For a time-periodic flow
$p$ is the pressure. For a time-periodic flow ![]() $\boldsymbol {q}_0(\boldsymbol {x},t)$, it satisfies
$\boldsymbol {q}_0(\boldsymbol {x},t)$, it satisfies ![]() $\boldsymbol {q}_0(\boldsymbol {x},t+T)=\boldsymbol {q}_0(\boldsymbol {x},t)$, where
$\boldsymbol {q}_0(\boldsymbol {x},t+T)=\boldsymbol {q}_0(\boldsymbol {x},t)$, where ![]() $T$ is the time period of the limit cycle and
$T$ is the time period of the limit cycle and ![]() ${\varOmega _n = 2{\rm \pi} /T}$ is the natural frequency of the system. Here, we define a phase
${\varOmega _n = 2{\rm \pi} /T}$ is the natural frequency of the system. Here, we define a phase ![]() $\theta$ such that
$\theta$ such that
With the definition of ![]() $\theta$, we can identify the full state vector of the limit cycle solution
$\theta$, we can identify the full state vector of the limit cycle solution ![]() $\boldsymbol {q}_0(\boldsymbol {x},\theta )$ at every
$\boldsymbol {q}_0(\boldsymbol {x},\theta )$ at every ![]() $\theta$.
$\theta$.
Given a stable limit cycle solution, with the frequency of the limit cycle being ![]() $\varOmega _n$, the phase in the vicinity of the limit cycle can be described using the generalized phase variable
$\varOmega _n$, the phase in the vicinity of the limit cycle can be described using the generalized phase variable ![]() $\varTheta (\boldsymbol {q}(\boldsymbol {x},t))$. Thus, the generalized phase dynamics is described as
$\varTheta (\boldsymbol {q}(\boldsymbol {x},t))$. Thus, the generalized phase dynamics is described as
Leveraging the phase dynamics, we can derive the phase response to sufficiently small perturbations,
which provides the corresponding change to phase dynamics as
 \begin{align} \dot{\theta}(t)=\dot{\varTheta}(\boldsymbol{q}) &= \int_{\mathcal{D}}\boldsymbol{\nabla}_{\boldsymbol{q}} \varTheta(\boldsymbol{q}) \boldsymbol{\cdot} \dot{\boldsymbol{q}} \,{\rm d}\,\boldsymbol{x} = \int_{\mathcal{D}} \boldsymbol{\nabla}_{\boldsymbol{q}} \varTheta(\boldsymbol{q}) \boldsymbol{\cdot} [\mathcal{N}(\boldsymbol{q}(\boldsymbol{x},t))+\epsilon \boldsymbol{F}(\boldsymbol{x},t)]\, {\rm d}\,\boldsymbol{x}\nonumber\\ &\approx \varOmega_n + \epsilon\int_{\mathcal{D}}\boldsymbol{Z}(\boldsymbol{x},\theta) \boldsymbol{\cdot}\boldsymbol{F}(\boldsymbol{x},t) \,{\rm d}\,\boldsymbol{x}. \end{align}
\begin{align} \dot{\theta}(t)=\dot{\varTheta}(\boldsymbol{q}) &= \int_{\mathcal{D}}\boldsymbol{\nabla}_{\boldsymbol{q}} \varTheta(\boldsymbol{q}) \boldsymbol{\cdot} \dot{\boldsymbol{q}} \,{\rm d}\,\boldsymbol{x} = \int_{\mathcal{D}} \boldsymbol{\nabla}_{\boldsymbol{q}} \varTheta(\boldsymbol{q}) \boldsymbol{\cdot} [\mathcal{N}(\boldsymbol{q}(\boldsymbol{x},t))+\epsilon \boldsymbol{F}(\boldsymbol{x},t)]\, {\rm d}\,\boldsymbol{x}\nonumber\\ &\approx \varOmega_n + \epsilon\int_{\mathcal{D}}\boldsymbol{Z}(\boldsymbol{x},\theta) \boldsymbol{\cdot}\boldsymbol{F}(\boldsymbol{x},t) \,{\rm d}\,\boldsymbol{x}. \end{align} Here, ![]() $\boldsymbol {Z}(\boldsymbol {x},\theta )= \boldsymbol {\nabla }_{\boldsymbol {q}}\varTheta (\boldsymbol {q})|_{\boldsymbol {q}= \boldsymbol {q}_0(\boldsymbol {x},\theta )}$ is the spatial phase sensitivity field as it quantifies the phase response of the system to any given small perturbation and
$\boldsymbol {Z}(\boldsymbol {x},\theta )= \boldsymbol {\nabla }_{\boldsymbol {q}}\varTheta (\boldsymbol {q})|_{\boldsymbol {q}= \boldsymbol {q}_0(\boldsymbol {x},\theta )}$ is the spatial phase sensitivity field as it quantifies the phase response of the system to any given small perturbation and ![]() $\mathcal {D}$ is the considered spatial domain. This spatial phase sensitivity field can be obtained using either a direct impulse-based method (Taira & Nakao Reference Taira and Nakao2018; Khodkar & Taira Reference Khodkar and Taira2020; Loe et al. Reference Loe, Nakao, Jimbo and Kotani2021; Nair et al. Reference Nair, Taira, Brunton and Brunton2021), or an adjoint-based approach (Kawamura & Nakao Reference Kawamura and Nakao2013, Reference Kawamura and Nakao2015; Kawamura et al. Reference Kawamura, Godavarthi and Taira2022), or a Jacobian-free approach (Iima Reference Iima2021). We use the adjoint-based phase reduction framework to obtain the phase sensitivity fields in the present study, as we can obtain the high-fidelity
$\mathcal {D}$ is the considered spatial domain. This spatial phase sensitivity field can be obtained using either a direct impulse-based method (Taira & Nakao Reference Taira and Nakao2018; Khodkar & Taira Reference Khodkar and Taira2020; Loe et al. Reference Loe, Nakao, Jimbo and Kotani2021; Nair et al. Reference Nair, Taira, Brunton and Brunton2021), or an adjoint-based approach (Kawamura & Nakao Reference Kawamura and Nakao2013, Reference Kawamura and Nakao2015; Kawamura et al. Reference Kawamura, Godavarthi and Taira2022), or a Jacobian-free approach (Iima Reference Iima2021). We use the adjoint-based phase reduction framework to obtain the phase sensitivity fields in the present study, as we can obtain the high-fidelity ![]() $\boldsymbol {Z}(\boldsymbol {x},\theta )$ in all the flow variables by solving a single pair of forward and adjoint simulations.
$\boldsymbol {Z}(\boldsymbol {x},\theta )$ in all the flow variables by solving a single pair of forward and adjoint simulations.
2.2. Adjoint-based approach for phase sensitivity fields
We utilize the adjoint-based formulation to find the phase sensitivity fields ![]() $\boldsymbol {Z}$ for time-periodic wakes. Let us consider the dynamics of a small perturbation
$\boldsymbol {Z}$ for time-periodic wakes. Let us consider the dynamics of a small perturbation ![]() $\boldsymbol {q}^\prime (\boldsymbol {x},\theta,t)$ by linearizing the Navier–Stokes equations about the periodic base state
$\boldsymbol {q}^\prime (\boldsymbol {x},\theta,t)$ by linearizing the Navier–Stokes equations about the periodic base state ![]() $\boldsymbol {q}_0(\boldsymbol {x},\theta )$. The perturbation dynamics is given by
$\boldsymbol {q}_0(\boldsymbol {x},\theta )$. The perturbation dynamics is given by ![]() $\dot {\boldsymbol {q}}^\prime = \mathcal {L}(\boldsymbol {x},\theta )\boldsymbol {q}^\prime$, where
$\dot {\boldsymbol {q}}^\prime = \mathcal {L}(\boldsymbol {x},\theta )\boldsymbol {q}^\prime$, where ![]() $\mathcal {L}(\boldsymbol {x},\theta )$ is the linearized Navier–Stokes operator.
$\mathcal {L}(\boldsymbol {x},\theta )$ is the linearized Navier–Stokes operator.
To obtain the phase dynamics of the dominant limit cycle oscillation, we consider Floquet eigenfunction ![]() $\boldsymbol {Q}$ and adjoint eigenfunction
$\boldsymbol {Q}$ and adjoint eigenfunction ![]() $\boldsymbol {Q}^*$ corresponding to the zero eigenvalue. This Floquet-zero eigenvalue corresponds to the phase degree of freedom for the stable limit cycle dynamics. Thus phase dynamics is obtained by projecting the perturbed dynamics in (2.4) on the adjoint eigenfunction as
$\boldsymbol {Q}^*$ corresponding to the zero eigenvalue. This Floquet-zero eigenvalue corresponds to the phase degree of freedom for the stable limit cycle dynamics. Thus phase dynamics is obtained by projecting the perturbed dynamics in (2.4) on the adjoint eigenfunction as
 \begin{align} \dot{\theta}(t) &= \int_{\mathcal{D}} [ \boldsymbol{Q}^*(\boldsymbol{x},\theta) \boldsymbol{\cdot} \mathcal{N}(\boldsymbol{q})+\epsilon \boldsymbol{Q}^*(\boldsymbol{x},\theta) \boldsymbol{\cdot} \boldsymbol{F}(\boldsymbol{x},t) ]\, {\rm d}\,\boldsymbol{x} \nonumber\\ &\approx \varOmega_n + \epsilon \int_{\mathcal{D}} \boldsymbol{Q}^*(\boldsymbol{x},\theta) \boldsymbol{\cdot} \boldsymbol{F}(\boldsymbol{x},t) \,{\rm d}\,\boldsymbol{x}. \end{align}
\begin{align} \dot{\theta}(t) &= \int_{\mathcal{D}} [ \boldsymbol{Q}^*(\boldsymbol{x},\theta) \boldsymbol{\cdot} \mathcal{N}(\boldsymbol{q})+\epsilon \boldsymbol{Q}^*(\boldsymbol{x},\theta) \boldsymbol{\cdot} \boldsymbol{F}(\boldsymbol{x},t) ]\, {\rm d}\,\boldsymbol{x} \nonumber\\ &\approx \varOmega_n + \epsilon \int_{\mathcal{D}} \boldsymbol{Q}^*(\boldsymbol{x},\theta) \boldsymbol{\cdot} \boldsymbol{F}(\boldsymbol{x},t) \,{\rm d}\,\boldsymbol{x}. \end{align}
We note that the norm of ![]() $\boldsymbol {Q}^*$ is arbitrary and the normalization condition of
$\boldsymbol {Q}^*$ is arbitrary and the normalization condition of ![]() $\boldsymbol {Q}^*$ is appropriately chosen to satisfy
$\boldsymbol {Q}^*$ is appropriately chosen to satisfy ![]() $\int _{\mathcal {D}} [ \boldsymbol {Q}^*(\boldsymbol {x},\theta ) \boldsymbol {\cdot } \mathcal {N}(\boldsymbol {q}) ] \,\textrm{d}\,\boldsymbol{x}=\varOmega _n$ for all
$\int _{\mathcal {D}} [ \boldsymbol {Q}^*(\boldsymbol {x},\theta ) \boldsymbol {\cdot } \mathcal {N}(\boldsymbol {q}) ] \,\textrm{d}\,\boldsymbol{x}=\varOmega _n$ for all ![]() $\theta$.
$\theta$.
More details on the properties of ![]() $\boldsymbol {Q}^*$ are given in our earlier work (Kawamura et al. Reference Kawamura, Godavarthi and Taira2022). Here, by comparing (2.6) and (2.5), for perturbations in the form of velocity, we obtain
$\boldsymbol {Q}^*$ are given in our earlier work (Kawamura et al. Reference Kawamura, Godavarthi and Taira2022). Here, by comparing (2.6) and (2.5), for perturbations in the form of velocity, we obtain ![]() $\boldsymbol {Z}(\boldsymbol {x},\theta ) = \boldsymbol {Q}^*(\boldsymbol {x},\theta )$. Hence, phase sensitivity is the adjoint-zero eigenfunction of the linearized Navier–Stokes operator. The spatial phase sensitivity fields can be obtained by solving the dynamics, which in two dimensions is governed by the linearized adjoint equations of
$\boldsymbol {Z}(\boldsymbol {x},\theta ) = \boldsymbol {Q}^*(\boldsymbol {x},\theta )$. Hence, phase sensitivity is the adjoint-zero eigenfunction of the linearized Navier–Stokes operator. The spatial phase sensitivity fields can be obtained by solving the dynamics, which in two dimensions is governed by the linearized adjoint equations of
 \begin{equation} \left.\begin{gathered} \frac{\partial }{\partial t}\boldsymbol{Q}^*(\boldsymbol{x},-\varOmega_n t) ={-}U^* \boldsymbol{\nabla} u -V^* \boldsymbol{\nabla} v + \boldsymbol{q} \boldsymbol{\cdot}\boldsymbol{\nabla} \boldsymbol{Q}^*-\boldsymbol{\nabla} P^* +\frac{1}{Re}\nabla^2\boldsymbol{Q}^*,\\ \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{Q}^* =0, \end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered} \frac{\partial }{\partial t}\boldsymbol{Q}^*(\boldsymbol{x},-\varOmega_n t) ={-}U^* \boldsymbol{\nabla} u -V^* \boldsymbol{\nabla} v + \boldsymbol{q} \boldsymbol{\cdot}\boldsymbol{\nabla} \boldsymbol{Q}^*-\boldsymbol{\nabla} P^* +\frac{1}{Re}\nabla^2\boldsymbol{Q}^*,\\ \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{Q}^* =0, \end{gathered}\right\}\end{equation}
where ![]() $\boldsymbol {Q}^*=(U^*, V^*)$ and
$\boldsymbol {Q}^*=(U^*, V^*)$ and ![]() $\boldsymbol {q}=(u,v)$.
$\boldsymbol {q}=(u,v)$.
Thus, the phase sensitivity fields with respect to perturbations in the velocity field are obtained by seeking a periodic solution for (2.1) and solving the system of adjoint equations (2.7). Since, the adjoint equations are analogous to the Navier–Stokes equations, the same numerical scheme can be used to solve them. An overview of the phase description for airfoil wakes is shown in figure 2. The phase is defined based on the lift coefficient ![]() $C_L{-}\dot{C}_L$ plane, where
$C_L{-}\dot{C}_L$ plane, where ![]() $\theta =0,{\rm \pi}$ correspond to mean
$\theta =0,{\rm \pi}$ correspond to mean ![]() $C_L$,
$C_L$, ![]() $\theta = {\rm \pi}/2$ corresponds to maximum
$\theta = {\rm \pi}/2$ corresponds to maximum ![]() $C_L$ and
$C_L$ and ![]() $\theta =3{\rm \pi} /2$ corresponds to minimum
$\theta =3{\rm \pi} /2$ corresponds to minimum ![]() $C_L$ (Taira & Nakao Reference Taira and Nakao2018).
$C_L$ (Taira & Nakao Reference Taira and Nakao2018).

Figure 2. An overview of the phase reduction approach for flow over a NACA0012 airfoil at ![]() $\alpha =45^\circ$ and
$\alpha =45^\circ$ and ![]() ${Re}=100$. (a) Definition of phase based on the lift coefficient,
${Re}=100$. (a) Definition of phase based on the lift coefficient, ![]() $C_L{-}\dot {C}_L$ plane. (b) Instantaneous spatial phase sensitivity fields
$C_L{-}\dot {C}_L$ plane. (b) Instantaneous spatial phase sensitivity fields ![]() $Z_u$ and
$Z_u$ and ![]() $Z_v$ with respect to the perturbations in velocity fields.
$Z_v$ with respect to the perturbations in velocity fields.
2.3. Synchronization analysis to external periodic forcing
Establishing this oscillator dynamics enables us to study the synchronization characteristics of the system to an external periodic forcing signal with a frequency ![]() $\varOmega _f$ different from the wake shedding frequency
$\varOmega _f$ different from the wake shedding frequency ![]() $\varOmega _n$. We introduce a localized periodic forcing at location
$\varOmega _n$. We introduce a localized periodic forcing at location ![]() $\boldsymbol {x}_0$ at a forcing frequency
$\boldsymbol {x}_0$ at a forcing frequency ![]() $\varOmega _f$. The spatial profile of forcing is given by a Dirac delta function
$\varOmega _f$. The spatial profile of forcing is given by a Dirac delta function ![]() $h(\boldsymbol {x})=\delta (\boldsymbol {x}-\boldsymbol {x}_0)$. Using (2.5), the governing phase dynamics becomes
$h(\boldsymbol {x})=\delta (\boldsymbol {x}-\boldsymbol {x}_0)$. Using (2.5), the governing phase dynamics becomes
where ![]() $\boldsymbol {F}(\boldsymbol {x},t)=\boldsymbol {f}(\varOmega _f t)h(\boldsymbol {x})$ and the local phase sensitivity function is given by
$\boldsymbol {F}(\boldsymbol {x},t)=\boldsymbol {f}(\varOmega _f t)h(\boldsymbol {x})$ and the local phase sensitivity function is given by ![]() ${\boldsymbol {\zeta }(\theta ) = \int _{\mathcal {D}} \boldsymbol {Z}(\boldsymbol {x},\theta ) h(\boldsymbol {x}) \,\textrm{d}\,\boldsymbol{x}=\boldsymbol {Z}(\boldsymbol {x}_0,\theta )}$.
${\boldsymbol {\zeta }(\theta ) = \int _{\mathcal {D}} \boldsymbol {Z}(\boldsymbol {x},\theta ) h(\boldsymbol {x}) \,\textrm{d}\,\boldsymbol{x}=\boldsymbol {Z}(\boldsymbol {x}_0,\theta )}$.
To characterize the synchronization of the system to external forcing, we consider the relative phase ![]() $\phi (t)$ between the phase of the system
$\phi (t)$ between the phase of the system ![]() $\theta (t)$ and that of the forcing signal
$\theta (t)$ and that of the forcing signal ![]() $\varOmega _f t$ as
$\varOmega _f t$ as ![]() $\phi (t) = \theta (t) - \varOmega _f t$. The dynamics of the relative phase is provided as
$\phi (t) = \theta (t) - \varOmega _f t$. The dynamics of the relative phase is provided as
where ![]() $\Delta \varOmega = \varOmega _n-\varOmega _f$. The asymptotic behaviour of relative phase dynamics can be obtained by averaging over a period of forcing (Kuramoto Reference Kuramoto1984; Ermentrout & Kopell Reference Ermentrout and Kopell1991),
$\Delta \varOmega = \varOmega _n-\varOmega _f$. The asymptotic behaviour of relative phase dynamics can be obtained by averaging over a period of forcing (Kuramoto Reference Kuramoto1984; Ermentrout & Kopell Reference Ermentrout and Kopell1991),
where
 \begin{equation} \varGamma(\phi)=\frac{1}{2{\rm \pi}}\int\limits_{0}^{2{\rm \pi}} \boldsymbol{\zeta}(\phi+\psi)\boldsymbol{\cdot} \boldsymbol{f}(\psi) \,{\rm d}\psi \end{equation}
\begin{equation} \varGamma(\phi)=\frac{1}{2{\rm \pi}}\int\limits_{0}^{2{\rm \pi}} \boldsymbol{\zeta}(\phi+\psi)\boldsymbol{\cdot} \boldsymbol{f}(\psi) \,{\rm d}\psi \end{equation}
is the phase coupling function and ![]() $\Delta \varOmega = \varOmega _n - \varOmega _f$. Synchronization occurs if the relative phase becomes a constant, i.e.
$\Delta \varOmega = \varOmega _n - \varOmega _f$. Synchronization occurs if the relative phase becomes a constant, i.e. ![]() $\dot {\phi }\rightarrow 0$. Hence, the synchronization condition is given as
$\dot {\phi }\rightarrow 0$. Hence, the synchronization condition is given as
The synchronization condition determines the forcing frequency required to synchronize the dynamics to the external actuation based on the phase coupling function.
We aim to identify the optimal periodic actuation to synchronize the system to a forcing frequency as quickly as possible. Hence, the rate of convergence of ![]() $\phi$ to a fixed point
$\phi$ to a fixed point ![]() $\phi _*$ should be maximized to satisfy
$\phi _*$ should be maximized to satisfy
Therefore, we can formulate an optimization problem to maximize ![]() $|\dot {\phi }|$, which occurs when
$|\dot {\phi }|$, which occurs when ![]() $-\epsilon \varGamma ^\prime (\phi _*)$ is large. Here
$-\epsilon \varGamma ^\prime (\phi _*)$ is large. Here ![]() $-\varGamma ^\prime (\phi _*)$ is the synchronization speed
$-\varGamma ^\prime (\phi _*)$ is the synchronization speed ![]() $S$. The cost function
$S$. The cost function ![]() $\mathcal {J}$ is therefore formulated as
$\mathcal {J}$ is therefore formulated as
where ![]() $\lambda$ and
$\lambda$ and ![]() $\mu$ are Lagrangian multipliers and
$\mu$ are Lagrangian multipliers and ![]() $\langle \,\cdot \,\rangle = ({1}/(2{\rm \pi} ))\int _0^{2{\rm \pi} }(\,\cdot \,) \,\textrm {d}\theta$. The first term corresponds to maximizing the synchronization speed, the second term constrains the energy of actuation, and the third term directly follows from (2.13).
$\langle \,\cdot \,\rangle = ({1}/(2{\rm \pi} ))\int _0^{2{\rm \pi} }(\,\cdot \,) \,\textrm {d}\theta$. The first term corresponds to maximizing the synchronization speed, the second term constrains the energy of actuation, and the third term directly follows from (2.13).
Since the synchronization is independent of the initial phase, without loss of generality, we consider the fixed point, ![]() $\phi _*=0$. This optimization can be solved analytically using the calculus of variations (Zlotnik et al. Reference Zlotnik, Chen, Kiss, Tanaka and Li2013). The optimal waveform for fast synchronization can then be derived as
$\phi _*=0$. This optimization can be solved analytically using the calculus of variations (Zlotnik et al. Reference Zlotnik, Chen, Kiss, Tanaka and Li2013). The optimal waveform for fast synchronization can then be derived as
 \begin{equation} \boldsymbol{f}(\theta;\Delta \varOmega/\epsilon) ={-}\frac{\boldsymbol{\zeta}^\prime(\theta)}{2\lambda} - \frac{(\Delta \varOmega /\epsilon)\boldsymbol{\zeta}(\theta)} {\langle\boldsymbol{\zeta}\boldsymbol{\cdot} \boldsymbol{\zeta}\rangle},\quad \lambda = \frac{1}{2}\sqrt{\frac{\langle \boldsymbol{\zeta}^\prime \boldsymbol{\cdot} \boldsymbol{\zeta}^\prime\rangle }{1-\dfrac{(\Delta \varOmega/\epsilon)^2}{ \langle \boldsymbol{\zeta} \boldsymbol{\cdot} \boldsymbol{\zeta} \rangle}}}. \end{equation}
\begin{equation} \boldsymbol{f}(\theta;\Delta \varOmega/\epsilon) ={-}\frac{\boldsymbol{\zeta}^\prime(\theta)}{2\lambda} - \frac{(\Delta \varOmega /\epsilon)\boldsymbol{\zeta}(\theta)} {\langle\boldsymbol{\zeta}\boldsymbol{\cdot} \boldsymbol{\zeta}\rangle},\quad \lambda = \frac{1}{2}\sqrt{\frac{\langle \boldsymbol{\zeta}^\prime \boldsymbol{\cdot} \boldsymbol{\zeta}^\prime\rangle }{1-\dfrac{(\Delta \varOmega/\epsilon)^2}{ \langle \boldsymbol{\zeta} \boldsymbol{\cdot} \boldsymbol{\zeta} \rangle}}}. \end{equation} Hence, once we compute the local phase sensitivity function ![]() $\boldsymbol {\zeta }(\theta )$, the optimal waveform for fast synchronization can be analytically found using (2.15a,b) for various
$\boldsymbol {\zeta }(\theta )$, the optimal waveform for fast synchronization can be analytically found using (2.15a,b) for various ![]() $\varOmega _f$ and
$\varOmega _f$ and ![]() $\epsilon$. The optimal speed of synchronization is characterized by then computing
$\epsilon$. The optimal speed of synchronization is characterized by then computing ![]() $-\varGamma ^\prime (0)$ using the optimal waveform given by (2.15a,b). Even though the current formulation to obtain the optimal waveform is defined for a single pointwise actuation, this directly extends to the case with multiple pointwise actuators or spatially distributed actuators following from (2.5). This is reflected as a change in the inner product
$-\varGamma ^\prime (0)$ using the optimal waveform given by (2.15a,b). Even though the current formulation to obtain the optimal waveform is defined for a single pointwise actuation, this directly extends to the case with multiple pointwise actuators or spatially distributed actuators following from (2.5). This is reflected as a change in the inner product ![]() $\langle \,\cdot \, \rangle$ in (2.14) and (2.15a,b), where the inner product would be computed as an integration for the multiple local phase sensitivities and actuation waveforms. Next, we uncover these optimal waveforms for the airfoil wakes using the local phase sensitivity functions and assess their performance for fast synchronization.
$\langle \,\cdot \, \rangle$ in (2.14) and (2.15a,b), where the inner product would be computed as an integration for the multiple local phase sensitivities and actuation waveforms. Next, we uncover these optimal waveforms for the airfoil wakes using the local phase sensitivity functions and assess their performance for fast synchronization.
3. Phase synchronization analysis of airfoil wakes
3.1. Computational set-up
This study considers the two-dimensional incompressible laminar flow over NACA0012 airfoils at angles of attack, ![]() $\alpha =35^\circ$,
$\alpha =35^\circ$, ![]() $45^\circ$ and
$45^\circ$ and ![]() $55^\circ$ and chord-based Reynolds number of
$55^\circ$ and chord-based Reynolds number of ![]() ${Re}=U_\infty c/\nu =100$, where
${Re}=U_\infty c/\nu =100$, where ![]() $U_\infty$,
$U_\infty$, ![]() $c$ and
$c$ and ![]() $\nu$ are the free-stream velocity, airfoil chord length and kinematic viscosity, respectively. The flow dynamics is governed by incompressible Navier–Stokes equations (2.1) and the obtained flow fields present with periodic vortex shedding (Kawamura et al. Reference Kawamura, Godavarthi and Taira2022). The actuation in (2.4) is introduced as a localized force with the form
$\nu$ are the free-stream velocity, airfoil chord length and kinematic viscosity, respectively. The flow dynamics is governed by incompressible Navier–Stokes equations (2.1) and the obtained flow fields present with periodic vortex shedding (Kawamura et al. Reference Kawamura, Godavarthi and Taira2022). The actuation in (2.4) is introduced as a localized force with the form ![]() $\boldsymbol {F}(\boldsymbol {x},\varOmega _f t) = \boldsymbol {f}(\varOmega _f t)\delta (\boldsymbol {x}-\boldsymbol {x}_0)$, where
$\boldsymbol {F}(\boldsymbol {x},\varOmega _f t) = \boldsymbol {f}(\varOmega _f t)\delta (\boldsymbol {x}-\boldsymbol {x}_0)$, where ![]() $\boldsymbol {x}_0$ is a forcing location. The Dirac delta function is approximated with a three-cell discrete delta function (Roma, Peskin & Berger Reference Roma, Peskin and Berger1999).
$\boldsymbol {x}_0$ is a forcing location. The Dirac delta function is approximated with a three-cell discrete delta function (Roma, Peskin & Berger Reference Roma, Peskin and Berger1999).
The periodic flows over the airfoil are computed numerically through the immersed boundary projection method (Taira & Colonius Reference Taira and Colonius2007; Kajishima & Taira Reference Kajishima and Taira2016). For the numerical simulation, we consider a computational domain ![]() $\mathcal {D}=(x/c,y/c)\in [-16,16]\times [-30,30]$. The quarter-chord of the airfoil is placed at the origin. The smallest grid size is set to
$\mathcal {D}=(x/c,y/c)\in [-16,16]\times [-30,30]$. The quarter-chord of the airfoil is placed at the origin. The smallest grid size is set to ![]() $\Delta x_{min}/c = 0.02$, and the time step is chosen to be
$\Delta x_{min}/c = 0.02$, and the time step is chosen to be ![]() $\Delta t = 0.005$. The present computational set-up has been validated and is the same as that used in Kawamura et al. (Reference Kawamura, Godavarthi and Taira2022). The same computational set-up is used for adjoint simulations of the phase sensitivity fields.
$\Delta t = 0.005$. The present computational set-up has been validated and is the same as that used in Kawamura et al. (Reference Kawamura, Godavarthi and Taira2022). The same computational set-up is used for adjoint simulations of the phase sensitivity fields.
3.2. Synchronization analysis for airfoil wakes
The spatial phase sensitivity fields with respect to the streamwise and transverse velocity components ![]() $Z_u$ and
$Z_u$ and ![]() $Z_v$ for NACA0012 airfoils at
$Z_v$ for NACA0012 airfoils at ![]() $\alpha = 35^\circ$,
$\alpha = 35^\circ$, ![]() $45^\circ$ and
$45^\circ$ and ![]() $55^\circ$ are obtained through the adjoint-based approach described in § 2.2. Using the obtained spatial phase sensitivity fields, we can compute the optimal waveform for fast synchronization at each grid point as per equation (2.15a,b), which is then used to obtain the optimal synchronization speed at each grid point. We investigate the effect of the angle of attack on the synchronization speed and waveforms of NACA0012 airfoil wakes, as shown in figure 3. We consider the case when the forcing frequency
$55^\circ$ are obtained through the adjoint-based approach described in § 2.2. Using the obtained spatial phase sensitivity fields, we can compute the optimal waveform for fast synchronization at each grid point as per equation (2.15a,b), which is then used to obtain the optimal synchronization speed at each grid point. We investigate the effect of the angle of attack on the synchronization speed and waveforms of NACA0012 airfoil wakes, as shown in figure 3. We consider the case when the forcing frequency ![]() $\varOmega _f =\varOmega _n$ and
$\varOmega _f =\varOmega _n$ and ![]() $\Delta \varOmega =0$. It follows from (2.15a,b) that the optimal actuation waveform at each point is proportional to the corresponding derivative of the local phase sensitivity function
$\Delta \varOmega =0$. It follows from (2.15a,b) that the optimal actuation waveform at each point is proportional to the corresponding derivative of the local phase sensitivity function ![]() $\boldsymbol {\zeta }^\prime (\theta )$.
$\boldsymbol {\zeta }^\prime (\theta )$.

Figure 3. (a–c) Synchronization speed ![]() $S$ around a NACA0012 airfoil at
$S$ around a NACA0012 airfoil at ![]() $\alpha =35^\circ$,
$\alpha =35^\circ$, ![]() $45^\circ$ and
$45^\circ$ and ![]() $55^\circ$. The black dots indicate local maxima. (d–e) Theoretical optimal waveforms for fast synchronization with pointwise forcing at the leading and trailing edges for
$55^\circ$. The black dots indicate local maxima. (d–e) Theoretical optimal waveforms for fast synchronization with pointwise forcing at the leading and trailing edges for ![]() $\alpha =35^\circ$,
$\alpha =35^\circ$, ![]() $45^\circ$ and
$45^\circ$ and ![]() $55^\circ$.
$55^\circ$.
The spatial distributions of synchronization speed ![]() $S$ around the airfoil found using the optimal waveform for
$S$ around the airfoil found using the optimal waveform for ![]() $\alpha = 35^\circ$,
$\alpha = 35^\circ$, ![]() $45^\circ$ and
$45^\circ$ and ![]() $55^\circ$ are depicted in figures 3(a)–3(c). As the angle of attack increases, the overall magnitude of the synchronization speed decreases, indicating an increased difficulty in synchronization for higher post-stall angles of attack. With an increase in
$55^\circ$ are depicted in figures 3(a)–3(c). As the angle of attack increases, the overall magnitude of the synchronization speed decreases, indicating an increased difficulty in synchronization for higher post-stall angles of attack. With an increase in ![]() $\alpha$, we observe stronger and larger leading- and trailing-edge vortex structures. To achieve synchronization with external forcing, the vortex formation time and the length scale have to be modified. This therefore becomes challenging with higher
$\alpha$, we observe stronger and larger leading- and trailing-edge vortex structures. To achieve synchronization with external forcing, the vortex formation time and the length scale have to be modified. This therefore becomes challenging with higher ![]() $\alpha$, which is reflected in reduced synchronization speed. Further, we also note that the white region around the airfoil corresponds to a small optimal synchronization speed, indicating that, irrespective of the actuation energy, these spatial locations are not conducive for flow modification. This means that the actuation effort must penetrate the outside of the boundary layer.
$\alpha$, which is reflected in reduced synchronization speed. Further, we also note that the white region around the airfoil corresponds to a small optimal synchronization speed, indicating that, irrespective of the actuation energy, these spatial locations are not conducive for flow modification. This means that the actuation effort must penetrate the outside of the boundary layer.
We also observed that, for all ![]() $\alpha$, the local maxima in the synchronization speed are attained near the leading and trailing edges, suggesting them as optimal actuation locations for synchronization (indicated as black dots). The leading and trailing edges are the most sensitive regions since they are specific regions in the flow field with high curvature. Further, the regions with high synchronization speed become more compact and are concentrated at the leading and trailing edges with an increase in
$\alpha$, the local maxima in the synchronization speed are attained near the leading and trailing edges, suggesting them as optimal actuation locations for synchronization (indicated as black dots). The leading and trailing edges are the most sensitive regions since they are specific regions in the flow field with high curvature. Further, the regions with high synchronization speed become more compact and are concentrated at the leading and trailing edges with an increase in ![]() $\alpha$ due to the earlier flow separation and the concentration of gradients at the leading and trailing edges at higher
$\alpha$ due to the earlier flow separation and the concentration of gradients at the leading and trailing edges at higher ![]() $\alpha$. Even though we considered three angles of attack, we expect this trend in synchronization speed and optimal waveform to hold true for much higher angles of attack.
$\alpha$. Even though we considered three angles of attack, we expect this trend in synchronization speed and optimal waveform to hold true for much higher angles of attack.
For the NACA0012 airfoil at ![]() $Re=100$, we observe a steady wake until
$Re=100$, we observe a steady wake until ![]() $\alpha \approx 20^\circ$. This results in a constant lift coefficient and, hence, an ill-defined phase. Further, as
$\alpha \approx 20^\circ$. This results in a constant lift coefficient and, hence, an ill-defined phase. Further, as ![]() $\alpha \rightarrow 90^\circ$, we approach a zero mean lift coefficient. However, for
$\alpha \rightarrow 90^\circ$, we approach a zero mean lift coefficient. However, for ![]() $30^\circ \leqslant \alpha \leqslant 90^\circ$, we observe periodic vortex shedding and we can leverage the optimal waveform analysis. We expect a similar trend in the optimal waveform and in the synchronization speed with an increase in the angle of attack. An increase in the angle of attack results in the formation of stronger leading- and trailing-edge vortices, thereby increasing the difficulty in synchronization and the reduction in synchronization speed. The asymmetry in the vortex formation and roll-up between the leading- and trailing-edge vortices also increases with most
$30^\circ \leqslant \alpha \leqslant 90^\circ$, we observe periodic vortex shedding and we can leverage the optimal waveform analysis. We expect a similar trend in the optimal waveform and in the synchronization speed with an increase in the angle of attack. An increase in the angle of attack results in the formation of stronger leading- and trailing-edge vortices, thereby increasing the difficulty in synchronization and the reduction in synchronization speed. The asymmetry in the vortex formation and roll-up between the leading- and trailing-edge vortices also increases with most ![]() $\alpha$, resulting in a non-sinusoidal optimal waveform. However, for
$\alpha$, resulting in a non-sinusoidal optimal waveform. However, for ![]() $\alpha \rightarrow 90^\circ$, we approach a symmetric bluff-body vortex shedding. Hence, overall, the optimal waveform outperforms the synchronization speed of a sinusoidal waveform at most higher angles of attack. It is noteworthy that, due to the difficulty in synchronization at higher angles of attack, we will require a larger actuation effort to synchronize the wake to a different frequency.
$\alpha \rightarrow 90^\circ$, we approach a symmetric bluff-body vortex shedding. Hence, overall, the optimal waveform outperforms the synchronization speed of a sinusoidal waveform at most higher angles of attack. It is noteworthy that, due to the difficulty in synchronization at higher angles of attack, we will require a larger actuation effort to synchronize the wake to a different frequency.
The optimal actuation waveforms in the ![]() $x$ and
$x$ and ![]() $y$ velocity directions, at the leading and trailing edges for various
$y$ velocity directions, at the leading and trailing edges for various ![]() $\alpha$, are shown in figures 3(d)–3(e). As
$\alpha$, are shown in figures 3(d)–3(e). As ![]() $\alpha$ increases, the optimal waveform becomes increasingly non-sinusoidal, due to the asymmetry in the vortex formation and shedding process near the leading and trailing edges at higher angles of attack. Further, the optimal waveform at the trailing edge at higher angles of attack suggests a smaller time duration where actuation is significant (for
$\alpha$ increases, the optimal waveform becomes increasingly non-sinusoidal, due to the asymmetry in the vortex formation and shedding process near the leading and trailing edges at higher angles of attack. Further, the optimal waveform at the trailing edge at higher angles of attack suggests a smaller time duration where actuation is significant (for ![]() $0<\theta <3{\rm \pi} /4$ in figure 3e), in comparison with the leading-edge optimal waveform. This is in line with flow physics, as we observe a more compact and stronger vortex roll-up at the trailing edge when compared to the vortex formation at the leading edge.
$0<\theta <3{\rm \pi} /4$ in figure 3e), in comparison with the leading-edge optimal waveform. This is in line with flow physics, as we observe a more compact and stronger vortex roll-up at the trailing edge when compared to the vortex formation at the leading edge.
We would like to point out that these optimal waveforms are obtained by independently maximizing the synchronization speed using the respective local phase sensitivity functions. We can also obtain the optimal waveforms at the leading and trailing edges by optimizing the synchronization speed using the local phase sensitivity functions simultaneously. For this present study, both these cases lead to similar results with minimal modification, where simultaneous optimization results in the same waveforms but with more actuation energy at the trailing edge than at the leading edge. This difference should be carefully considered for more complex flow fields when using multiple actuation locations.
Next, we numerically validate the synchronization analysis by introducing actuation at the optimal actuation locations near the leading and trailing edges (as shown in figure 3d–e). Here, we consider the optimal waveform and a sinusoidal waveform with the same averaged actuation direction at different forcing frequencies. We present the numerical results at ![]() $\alpha =45^\circ$ as a representative case. The numerical results of synchronization for a forcing frequency within
$\alpha =45^\circ$ as a representative case. The numerical results of synchronization for a forcing frequency within ![]() $5\,\%$ of the natural frequency are shown in figure 4. Here, we choose an actuation amplitude of
$5\,\%$ of the natural frequency are shown in figure 4. Here, we choose an actuation amplitude of ![]() $\epsilon =0.1$ to achieve synchronization for laminar flows at higher angles of attack.
$\epsilon =0.1$ to achieve synchronization for laminar flows at higher angles of attack.

Figure 4. Numerical results for synchronization analysis of the NACA0012 airfoil at ![]() $\alpha =45^\circ$. (a) Changes in
$\alpha =45^\circ$. (a) Changes in ![]() $C_L(t)$ at a forcing frequency
$C_L(t)$ at a forcing frequency ![]() $\varOmega _f=1.05\varOmega _n$. (b) Synchronization time using sinusoidal and optimal waveforms at different forcing frequencies. (c) Comparison of instantaneous vorticity fields for forcing frequencies,
$\varOmega _f=1.05\varOmega _n$. (b) Synchronization time using sinusoidal and optimal waveforms at different forcing frequencies. (c) Comparison of instantaneous vorticity fields for forcing frequencies, ![]() ${\varOmega _f=0.95\varOmega _n}$ and
${\varOmega _f=0.95\varOmega _n}$ and ![]() $\varOmega _f=1.05\varOmega _n$ with the unperturbed vorticity field.
$\varOmega _f=1.05\varOmega _n$ with the unperturbed vorticity field.
To assess the synchronization speed, we consider cycle-to-cycle variations of the ![]() $C_L$ coefficient and measure the inter-peak phase difference
$C_L$ coefficient and measure the inter-peak phase difference ![]() $\Delta \theta _k$ for each cycle as shown in figure 4(a). The optimal waveform actuation achieves synchronization in two shedding cycles, in comparison to
$\Delta \theta _k$ for each cycle as shown in figure 4(a). The optimal waveform actuation achieves synchronization in two shedding cycles, in comparison to ![]() ${O}(10)$ shedding cycles for the sinusoidal waveform (see figure 4b) for different forcing frequencies. Since the optimal waveform is based on the phase sensitivity function, it can efficiently identify the ‘when’ and ‘how’ to efficiently synchronize the system to an external forcing signal, thus achieving fast synchronization.
${O}(10)$ shedding cycles for the sinusoidal waveform (see figure 4b) for different forcing frequencies. Since the optimal waveform is based on the phase sensitivity function, it can efficiently identify the ‘when’ and ‘how’ to efficiently synchronize the system to an external forcing signal, thus achieving fast synchronization.
The effect of actuation frequency on flow physics is examined using the instantaneous vorticity fields of synchronized and unperturbed in figure 4(c). We observe streamwise elongation of the leading- and trailing-edge vortices for lower-frequency actuation, ![]() ${\varOmega _f = 0.95\varOmega _n}$, when compared with the unperturbed case. On the other hand, we observe more compact leading- and trailing-edge vortices for higher actuation frequencies,
${\varOmega _f = 0.95\varOmega _n}$, when compared with the unperturbed case. On the other hand, we observe more compact leading- and trailing-edge vortices for higher actuation frequencies, ![]() $\varOmega _f = 1.05\varOmega _n$. Hence, the modification of vortex shedding frequency through optimal waveform actuation is achieved by modifying the vortex formation length scale near the leading and trailing edges. Thus, the phase-sensitivity-based optimal waveform deviates from the sinusoidal waveform to target more actuation energy at the right time to achieve rapid flow modification.
$\varOmega _f = 1.05\varOmega _n$. Hence, the modification of vortex shedding frequency through optimal waveform actuation is achieved by modifying the vortex formation length scale near the leading and trailing edges. Thus, the phase-sensitivity-based optimal waveform deviates from the sinusoidal waveform to target more actuation energy at the right time to achieve rapid flow modification.
To further examine the effect of the present actuation over the lift coefficients, let us monitor the force elements (Chang Reference Chang1992). Force element theory enables us to identify the flow structures responsible for lift generation. We compute an auxiliary potential function ![]() $\phi _L$ that satisfies the Laplace equation
$\phi _L$ that satisfies the Laplace equation ![]() $\nabla ^2 \phi _L=0$, with the boundary condition
$\nabla ^2 \phi _L=0$, with the boundary condition ![]() $-\boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {\nabla }\phi _L= \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {e}_y$ on the airfoil surface, where
$-\boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {\nabla }\phi _L= \boldsymbol {n}\boldsymbol {\cdot }\boldsymbol {e}_y$ on the airfoil surface, where ![]() $\boldsymbol {e}_y$ is the unit vector in the lift direction. The lift force is obtained by taking the inner product of
$\boldsymbol {e}_y$ is the unit vector in the lift direction. The lift force is obtained by taking the inner product of ![]() $\boldsymbol {\nabla }\phi _L$ with the momentum equation and integrating with
$\boldsymbol {\nabla }\phi _L$ with the momentum equation and integrating with ![]() $\mathcal {D}$ in two dimensions as
$\mathcal {D}$ in two dimensions as
 \begin{equation} F_L = \int\limits_{\mathcal{D}} \boldsymbol{\omega} \times \boldsymbol{u} \boldsymbol{\cdot}\boldsymbol{\nabla} \phi_L \,{\rm d}D + \frac{1}{Re}\int\limits_{\partial \mathcal{D}} \boldsymbol{\omega} \times \boldsymbol{n} \boldsymbol{\cdot} (\boldsymbol{\nabla}\phi_L + \boldsymbol{e}_y) \,{\rm d}l, \end{equation}
\begin{equation} F_L = \int\limits_{\mathcal{D}} \boldsymbol{\omega} \times \boldsymbol{u} \boldsymbol{\cdot}\boldsymbol{\nabla} \phi_L \,{\rm d}D + \frac{1}{Re}\int\limits_{\partial \mathcal{D}} \boldsymbol{\omega} \times \boldsymbol{n} \boldsymbol{\cdot} (\boldsymbol{\nabla}\phi_L + \boldsymbol{e}_y) \,{\rm d}l, \end{equation}
where the first term denotes the surface integral and the second term denotes the line integral on the airfoil surface. The first integrand herein referred to the lift element ![]() $L_E$, and is used to monitor the effect of vortical structures on the lift force.
$L_E$, and is used to monitor the effect of vortical structures on the lift force.
The lift coefficient ![]() $C_L$ for a vortex shedding period for the unperturbed and the actuation frequencies
$C_L$ for a vortex shedding period for the unperturbed and the actuation frequencies ![]() ${\varOmega _f=0.95\varOmega _n}$ and
${\varOmega _f=0.95\varOmega _n}$ and ![]() $1.05 \varOmega _n$ are shown in figure 5. The snapshots are shown corresponding to the unperturbed flow fields (black), and synchronized flow fields at
$1.05 \varOmega _n$ are shown in figure 5. The snapshots are shown corresponding to the unperturbed flow fields (black), and synchronized flow fields at ![]() ${\varOmega _f=0.95\varOmega _n}$ (blue) and
${\varOmega _f=0.95\varOmega _n}$ (blue) and ![]() ${\varOmega _f =1.05\varOmega _n}$ (orange/red) at
${\varOmega _f =1.05\varOmega _n}$ (orange/red) at ![]() $\max C_L$ (
$\max C_L$ (![]() $\bigtriangleup$) and
$\bigtriangleup$) and ![]() $\min C_L$ (
$\min C_L$ (![]() $\bigtriangledown$). Owing to the actuation, we notice a significant change in
$\bigtriangledown$). Owing to the actuation, we notice a significant change in ![]() $C_L$ compared to the unperturbed case for both frequencies, especially for
$C_L$ compared to the unperturbed case for both frequencies, especially for ![]() $\varOmega _f=1.05\varOmega _n$. For a
$\varOmega _f=1.05\varOmega _n$. For a ![]() $5\,\%$ increase in frequency (
$5\,\%$ increase in frequency (![]() $\varOmega _f=1.05\varOmega _n$), we observe a
$\varOmega _f=1.05\varOmega _n$), we observe a ![]() $17\,\%$ increase in
$17\,\%$ increase in ![]() $\max C_L$ and a
$\max C_L$ and a ![]() $8\,\%$ increase in mean
$8\,\%$ increase in mean ![]() $C_L$ compared with the unperturbed case. However, we note that a similar amount of actuation is introduced to the flow field. It is noteworthy that the swift modification of the shedding timing is achieved by the lift increases for high-frequency actuation. We further analyse the wake with the lift elements
$C_L$ compared with the unperturbed case. However, we note that a similar amount of actuation is introduced to the flow field. It is noteworthy that the swift modification of the shedding timing is achieved by the lift increases for high-frequency actuation. We further analyse the wake with the lift elements ![]() $L_E$ (
$L_E$ (![]() $\bigtriangleup$) for unperturbed (black) and high-frequency (orange/red) actuation, as shown in figure 5. We observe a strong compact positive
$\bigtriangleup$) for unperturbed (black) and high-frequency (orange/red) actuation, as shown in figure 5. We observe a strong compact positive ![]() $L_E$ near the leading and trailing edges. This suggests that the increased strength and compactness of the vortex increases the local circulation, and thereby the lift force (Eldredge & Jones Reference Eldredge and Jones2019).
$L_E$ near the leading and trailing edges. This suggests that the increased strength and compactness of the vortex increases the local circulation, and thereby the lift force (Eldredge & Jones Reference Eldredge and Jones2019).

Figure 5. Characterization of ![]() $C_L$ for the NACA0012 airfoil at
$C_L$ for the NACA0012 airfoil at ![]() $\alpha = 45^\circ$ and
$\alpha = 45^\circ$ and ![]() ${Re}=100$. (a) Variation of
${Re}=100$. (a) Variation of ![]() $C_L$ when actuated with forcing frequencies
$C_L$ when actuated with forcing frequencies ![]() $\varOmega _f=1.05\varOmega _n$ and
$\varOmega _f=1.05\varOmega _n$ and ![]() $0.95\varOmega _n$. (b) Instantaneous lift force elements
$0.95\varOmega _n$. (b) Instantaneous lift force elements ![]() $L_E$ are shown for the actuated and unperturbed cases at
$L_E$ are shown for the actuated and unperturbed cases at ![]() $\max C_L$ (
$\max C_L$ (![]() $\bigtriangleup$) and
$\bigtriangleup$) and ![]() $\min C_L$ (
$\min C_L$ (![]() $\bigtriangledown$).
$\bigtriangledown$).
We now consider the low-frequency actuation (![]() $\varOmega _f=0.95\varOmega _n$), where we do not observe a significant change in mean
$\varOmega _f=0.95\varOmega _n$), where we do not observe a significant change in mean ![]() $C_L$ in comparison with the unperturbed case. In contrast to the high-frequency actuation, the optimal waveform actuation achieves a reduction in the wake shedding frequency through a reduction in
$C_L$ in comparison with the unperturbed case. In contrast to the high-frequency actuation, the optimal waveform actuation achieves a reduction in the wake shedding frequency through a reduction in ![]() $\min C_L$. The lift force elements
$\min C_L$. The lift force elements ![]() $L_E$ corresponding to this case (blue,
$L_E$ corresponding to this case (blue, ![]() $\bigtriangledown$) show a streamwise-elongated positive force element effectively pushing away the shear layer from the airfoil surface, thereby reducing the overall lift force. Overall, through the lift element theory, we identified that high-frequency actuation using the optimal waveform results in compact vortices at the leading and trailing edges, and the lower wake shedding frequency is achieved by streamwise elongation of the vortices at the leading and trailing edges. Through a high-frequency actuation using the optimal waveform, a transient increase in lift is observed, albeit with a considerable actuation effort. By demonstrating the effectiveness of optimal waveform analysis for
$\bigtriangledown$) show a streamwise-elongated positive force element effectively pushing away the shear layer from the airfoil surface, thereby reducing the overall lift force. Overall, through the lift element theory, we identified that high-frequency actuation using the optimal waveform results in compact vortices at the leading and trailing edges, and the lower wake shedding frequency is achieved by streamwise elongation of the vortices at the leading and trailing edges. Through a high-frequency actuation using the optimal waveform, a transient increase in lift is observed, albeit with a considerable actuation effort. By demonstrating the effectiveness of optimal waveform analysis for ![]() $\alpha =45^\circ$, we show the potential of this method for the analysis of a wide range of periodic fluid flows and their control in a transient manner.
$\alpha =45^\circ$, we show the potential of this method for the analysis of a wide range of periodic fluid flows and their control in a transient manner.
4. Conclusions
We presented a theoretical framework to find an optimal actuation waveform for maximizing the synchronization speed for periodic fluid flows. This was demonstrated for periodic post-stall airfoil wakes using localized forcing. We leveraged the phase reduction approach to identify the sensitivity with respect to the vortex shedding phases, thereby identifying the right time and direction of actuation for efficient synchronization. The optimal actuation waveform for fast synchronization departs from a sinusoidal waveform for higher angles of attack. We showed that the optimal waveform significantly outperforms the sinusoidal waveform in terms of synchronization speed.
We further identified that the modification of wake shedding frequency is achieved by the elongation of vortical structures for low frequency actuation, whereas synchronization to a higher frequency is achieved by compacting vortical structures near the leading and trailing edges. The present study based on phase reduction with an optimal waveform approach holds potential to develop transient flow control strategies that produce a quick response.
Funding
V.G. and K.T. acknowledge the support from the US Air Force Office of Scientific Research (grants FA9550-21-1-0178 and FA9550-22-1-0013) and the US National Science Foundation (grant 2129639). Y.K. acknowledges financial support from JSPS (Japan) KAKENHI grant numbers JP20K03797, JP18H03205 and JP17H03279. Y.K. also acknowledges support from Earth Simulator JAMSTEC Proposed Project.
Declaration of interests
The authors report no conflict of interest.