Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T19:12:18.130Z Has data issue: false hasContentIssue false
  • English
  • Français

Peristaltic pumping in thin non-axisymmetric annular tubes

Published online by Cambridge University Press:  23 April 2021

J. Brennen Carr Open the ORCID record for J. Brennen Carr [Opens in a new window] ,
John H. Thomas ,
Jia Liu  and
Jessica K. Shang Open the ORCID record for Jessica K. Shang [Opens in a new window]
J. Brennen Carr*
Affiliation:
Department of Mechanical Engineering, University of Rochester, Rochester, NY14627, USA
John H. Thomas
Affiliation:
Department of Mechanical Engineering, University of Rochester, Rochester, NY14627, USA
Jia Liu
Affiliation:
Department of Mechanical Engineering, University of Rochester, Rochester, NY14627, USA
Jessica K. Shang
Affiliation:
Department of Mechanical Engineering, University of Rochester, Rochester, NY14627, USA
*
†Email address for correspondence: jcarr12@ur.rochester.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

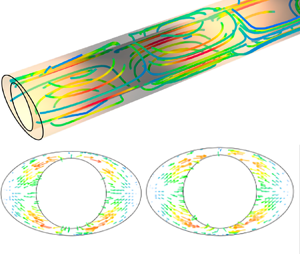
The two-dimensional laminar flow of a viscous fluid induced by peristalsis due to a moving wall wave has been studied previously for a rectangular channel, a circular tube and a concentric circular annulus. Here, we study peristaltic flow in a non-axisymmetric annular tube: in this case, the flow is three-dimensional, with motions in the azimuthal direction. This type of geometry is motivated by experimental observations of the pulsatile flow of cerebrospinal fluid along perivascular spaces surrounding arteries in the brain, which is at least partially driven by peristaltic pumping due to pulsations of the artery. These annular perivascular spaces are often eccentric and the outer boundary is seldom circular: their cross-sections can be well matched by a simple, adjustable model consisting of an inner circle (the outer wall of the artery) and an outer ellipse (the outer edge of the perivascular space), not necessarily concentric. We use this geometric model as a basis for numerical simulations of peristaltic flow: the adjustability of the model makes it suitable for other applications. We concentrate on the general effects of the non-axisymmetric configuration on the flow and do not attempt to specifically model perivascular pumping. We use a finite-element scheme to compute the flow in the annulus driven by a propagating sinusoidal radial displacement of the inner wall. Unlike the peristaltic flow in a concentric circular annulus, the flow is fully three-dimensional: azimuthal pressure variations drive an oscillatory flow in and out of the narrower gaps, inducing an azimuthal wiggle in the streamlines. We examine the dependence of the flow on the elongation of the outer elliptical wall and the eccentricity of the configuration. We find that the time-averaged volumetric flow is always in the same direction as the peristaltic wave and decreases with increasing ellipticity or eccentricity. The additional shearing motion in the azimuthal direction will increase mixing and enhance Taylor dispersion in these flows, effects that might have practical applications.

JFM classification

Biological Fluid Dynamics: Peristaltic pumping
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 917 , 25 June 2021 , A10
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aris, R. 1956 On the dispersion of a solute flowing through a tube. Proc. R. Soc. Lond. A 235, 69–77.Google Scholar
Asgari, M., de Zélicourt, D. & Kurtcuoglu, V. 2016 Glymphatic solute transport does not require bulk flow. Sci. Rep. 6, 38635.CrossRefGoogle Scholar
Bedussi, B., Almasian, M., de Vos, J., VanBavel, E. & Bakker, E.N.T.P. 2017 Paravascular spaces at the brain surface: low resistance pathways for cerebrospinal fluid flow. J. Cerebr. Blood F. Met. 38 (4), 719–726.CrossRefGoogle ScholarPubMed
Daversin-Catty, C., Vinje, V., Mardal, K.-A. & Rognes, M. 2020 The mechanisms behind perivascular fluid flow. PLoS ONE 15 (12), e0244442.CrossRefGoogle ScholarPubMed
Esmaily-Moghadam, M., Bazilevs, Y. & Marsden, A.L. 2015 Impact of data distribution on the parallel performance of iterative linear solvers with emphasis on CFD of incompressible flows. Comput. Mech. 55 (1), 93–103.CrossRefGoogle Scholar
Esmaily-Moghadam, M., Bazilevs, Y. & Marsden, A.L. 2013 A new preconditioning technique for implicitly coupled multidomain simulations with applications to hemodynamics. Comput. Mech. 52 (5), 1141–1152.CrossRefGoogle Scholar
Hadaczek, P., Yamashita, Y., Mirek, H., Tamas, L., Bohn, M.C., Noble, C., Park, J.W. & Bankiewicz, K. 2006 The ‘perivascular pump’ driven by arterial pulsation is a powerful mechanism for the distribution of therapeutic molecules within the brain. Mol. Ther. 14 (1), 69–78.CrossRefGoogle Scholar
Jaffrin, M.Y. & Shapiro, A.H. 1971 Peristaltic pumping. Annu. Rev. Fluid Mech. 3, 13–37.CrossRefGoogle Scholar
Kedarasetti, R.T., Drew, P.J. & Costanzo, F. 2020 Arterial pulsations drive oscillatory flow of CSF but not directional pumping. Sci. Rep. 10, 10102.CrossRefGoogle Scholar
Ladrón-de-Guevara, A., Shang, J.K., Nedergaard, M. & Kelley, D.H. 2020 Perivascular pumping in the mouse brain: realistic boundary conditions reconcile theory, simulation, and experiment. bioRxiv, https://www.biorxiv.org/content/early/2020/07/02/2020.07.02.183608.full.pdf.CrossRefGoogle Scholar
Mestre, H., Tithof, J., Du, T., Song, W., Peng, W., Sweeney, A.M., Olveda, G., Thomas, J.H., Nedergaard, M. & Kelley, D.H. 2018 Flow of cerebrospinal fluid is driven by arterial pulsations and is reduced in hypertension. Nat. Commun. 9 (1), 4878.CrossRefGoogle ScholarPubMed
Min-Rivas, F.G., Liu, J., Martell, B.C., Du, T., Mestre, H., Nedergaard, M., Tithof, J., Thomas, J.H. & Kelley, D.H. 2020 Surface periarterial spaces in the mouse brain are open, not porous (in preparation).CrossRefGoogle Scholar
Shapiro, A.H., Jaffrin, M.Y. & Weinberg, S.L. 1969 Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 37 (4), 799–825.CrossRefGoogle Scholar
Taylor, G.I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Thomas, J.H. 2019 Fluid dynamics of cerebrospinal fluid flow in perivascular spaces. J. R. Soc. Interface 16, 20190572.CrossRefGoogle ScholarPubMed
Tithof, J., Kelley, D.H., Mestre, H., Nedergaard, M. & Thomas, J.H. 2019 Hydraulic resistance of perivascular spaces in the brain. Fluids Barriers CNS 16, 19.CrossRefGoogle Scholar
Troyetsky, D.E., Tithof, J., Thomas, J.H. & Kelley, D.H. 2021 Dispersion as a waste-clearance mechanism in flow through penetrating perivascular spaces in the brain. Sci. Rep. 11, 4595.CrossRefGoogle Scholar
Updegrove, A., Wilson, N.M., Merkow, J., Lan, H., Marsden, A.L. & Shadden, S.C. 2017 Simvascular: an open source pipeline for cardiovascular simulation. Ann. Biomed. Engng 45 (3), 525–541.CrossRefGoogle ScholarPubMed
Wang, P. & Olbricht, W.L. 2011 Fluid mechanics in the perivascular space. J. Theor. Biol. 274 (1), 52–57.CrossRefGoogle ScholarPubMed
Williams, J.G., Turney, B.W., Moulton, D.E. & Waters, S.L. 2020 Effects of geometry on resistance in elliptical pipe flows. J. Fluid Mech. 891, A4.CrossRefGoogle Scholar