Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bizhani, M.
and
Frigaard, I. A.
2020.
Buoyancy effects on turbulent displacement of viscoplastic fluids from strongly eccentric horizontal annuli.
Physics of Fluids,
Vol. 32,
Issue. 12,
Foolad, Yasaman
Bizhani, Majid
and
Frigaard, Ian A.
2021.
A Comparative Study of Laminar-Turbulent Displacement in an Eccentric Annulus under Imposed Flow Rate and Imposed Pressure Drop Conditions.
Energies,
Vol. 14,
Issue. 6,
p.
1654.
Sarmadi, P.
Renteria, A.
and
Frigaard, I.A.
2021.
Primary cementing of horizontal wells. Displacement flows in eccentric horizontal annuli. Part 2. Computations.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Foroushan, Hanieh K.
Lund, Bjørnar
Ytrehus, Jan David
and
Saasen, Arild
2021.
Cement Placement: An Overview of Fluid Displacement Techniques and Modelling.
Energies,
Vol. 14,
Issue. 3,
p.
573.
Tan, Dongwen
Zhou, Xinping
Zhang, Gang
Zhu, Chengwei
and
Fu, Chenyu
2022.
Eccentricity effect on horizontal capillary emptying.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Zhang, R.
and
Frigaard, I.A.
2022.
Primary cementing of vertical wells: displacement and dispersion effects in narrow eccentric annuli.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Jung, H.
and
Frigaard, I.A.
2022.
Evaluation of common cementing practices affecting primary cementing quality.
Journal of Petroleum Science and Engineering,
Vol. 208,
Issue. ,
p.
109622.
Eslami, A.
Akbari, S.
and
Taghavi, S.M.
2022.
An experimental study of displacement flows in stationary and moving annuli for reverse circulation cementing applications.
Journal of Petroleum Science and Engineering,
Vol. 213,
Issue. ,
p.
110321.
Mitishita, Rodrigo S.
Waldal, Nile
Vogl, Anastasia
and
Frigaard, Ian A.
2022.
Turbulent displacement flows of viscoplastic fluids in obstructed eccentric annuli: Experiments.
Physics of Fluids,
Vol. 34,
Issue. 5,
Jung, H.
and
Frigaard, I. A.
2022.
Displacement flows in eccentric annuli with a rotating inner cylinder.
Physics of Fluids,
Vol. 34,
Issue. 5,
Mitishita, Rodrigo S.
Alishahi, Marzieh
and
Frigaard, Ian A.
2023.
Dynamics of displacement flows of viscoplastic fluids in obstructed eccentric annuli at moderate Reynolds numbers.
Physics of Fluids,
Vol. 35,
Issue. 11,
Zhang, R.
and
Frigaard, I.A.
2023.
Primary cementing of vertical wells: displacement and dispersion effects in narrow eccentric annuli. Part 2. Flow behaviour and classification.
Journal of Fluid Mechanics,
Vol. 972,
Issue. ,
Zhang, Ruizi
Ghorbani, Maryam
Wong, Sungshuen
and
Frigaard, Ian A.
2023.
Vertical cementing displacement flows of shear-thinning fluids.
Physics of Fluids,
Vol. 35,
Issue. 11,
Ghorbani, M.
Zhang, R.
Giljarhus, K. E. T.
Skadsem, H. J.
and
Frigaard, I. A.
2024.
Density unstable fluid displacement in vertical annuli.
Physics of Fluids,
Vol. 36,
Issue. 7,
Faramarzi, M.
Akbari, S.
and
Taghavi, S. M.
2024.
Buoyant miscible viscoplastic injections.
Physical Review Fluids,
Vol. 9,
Issue. 7,
Sotoudeh, Sophia
and
Frigaard, Ian A.
2024.
Computational study of Newtonian laminar annular horizontal displacement flows with rotating inner cylinder.
Physics of Fluids,
Vol. 36,
Issue. 8,
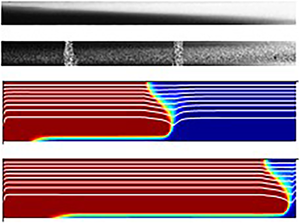
 $\approx$300 miscible Newtonian displacement flow experiments carried out in a dimensionally scaled laboratory set-up. Annulus eccentricity, density difference and viscosity of the fluids are varied, over a wide range of laminar Reynolds numbers. Comparisons with predictions from the two-dimensional gap-averaged (2DGA) model of Carrasco-Teja et al. (J. Fluid Mech., vol. 605, 2008, pp. 293–327) show excellent agreement in predicting the underlying competition between buoyancy and eccentricity, which results in either top side or slumping flows. Other features of the experiments are not predicted as well. The main discrepancy results from a variety of dispersive effects that are not present in the 2DGA model, e.g. dispersion within the annular gap and due to azimuthal secondary flows. We find that dispersive effects dominate to the extent that the slumping flows are best described by bulk diffusive spreading of the height-averaged concentrations, relative to the mean flow. A variety of flow structures and wave-like instabilities are discussed. The study is relevant to the oilfield process of primary cementing of horizontal wells.
$\approx$300 miscible Newtonian displacement flow experiments carried out in a dimensionally scaled laboratory set-up. Annulus eccentricity, density difference and viscosity of the fluids are varied, over a wide range of laminar Reynolds numbers. Comparisons with predictions from the two-dimensional gap-averaged (2DGA) model of Carrasco-Teja et al. (J. Fluid Mech., vol. 605, 2008, pp. 293–327) show excellent agreement in predicting the underlying competition between buoyancy and eccentricity, which results in either top side or slumping flows. Other features of the experiments are not predicted as well. The main discrepancy results from a variety of dispersive effects that are not present in the 2DGA model, e.g. dispersion within the annular gap and due to azimuthal secondary flows. We find that dispersive effects dominate to the extent that the slumping flows are best described by bulk diffusive spreading of the height-averaged concentrations, relative to the mean flow. A variety of flow structures and wave-like instabilities are discussed. The study is relevant to the oilfield process of primary cementing of horizontal wells.


