Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Harbig, R. R.
Sheridan, J.
and
Thompson, M. C.
2013.
Relationship between aerodynamic forces, flow structures and wing camber for rotating insect wing planforms.
Journal of Fluid Mechanics,
Vol. 730,
Issue. ,
p.
52.
Hartloper, Colin
and
Rival, David E.
2013.
Vortex development on pitching plates with lunate and truncate planforms.
Journal of Fluid Mechanics,
Vol. 732,
Issue. ,
p.
332.
Wong, Jaime G.
and
Rival, David E.
2013.
The Effect of Rotation on the Spanwise Transport of Vorticity in the Absence of Tip Effects.
Johansson, L. Christoffer
Engel, Sophia
Kelber, Almut
Klein Heerenbrink, Marco
and
Hedenström, Anders
2013.
Multiple leading edge vortices of unexpected strength in freely flying hawkmoth.
Scientific Reports,
Vol. 3,
Issue. 1,
Song, Jialei
Luo, Haoxiang
and
Hedrick, Tyson
2013.
Lift characteristics of a hovering rufous hummingbird.
Limacher, Eric J.
and
Rival, David E.
2014.
On the Stable Leading Edge Vortex in Rotating Systems.
Song, Jialei
Luo, Haoxiang
and
Hedrick, Tyson L.
2014.
Three-dimensional flow and lift characteristics of a hovering ruby-throated hummingbird.
Journal of The Royal Society Interface,
Vol. 11,
Issue. 98,
Wolfinger, M.
and
Rockwell, D.
2014.
Flow structure on a rotating wing: effect of radius of gyration.
Journal of Fluid Mechanics,
Vol. 755,
Issue. ,
p.
83.
Muijres, Florian T
Christoffer Johansson, L
Winter, York
and
Hedenström, Anders
2014.
Leading edge vortices in lesser long-nosed bats occurring at slow but not fast flight speeds.
Bioinspiration & Biomimetics,
Vol. 9,
Issue. 2,
p.
025006.
Noda, Ryusuke
Nakata, Toshiyuki
and
Liu, Hao
2014.
Effects of wing deformation on aerodynamic performance of a revolving insect wing.
Acta Mechanica Sinica,
Vol. 30,
Issue. 6,
p.
819.
Harbig, R. R.
Sheridan, J.
and
Thompson, M. C.
2014.
The role of advance ratio and aspect ratio in determining leading-edge vortex stability for flapping flight.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
p.
71.
Fu, Jun-Jiang
Hefler, Csaba
Qiu, Hui-He
and
Shyy, Wei
2014.
Effects of aspect ratio on flapping wing aerodynamics in animal flight.
Acta Mechanica Sinica,
Vol. 30,
Issue. 6,
p.
776.
Beals, Nathan E.
and
Jones, Anya R.
2014.
The Effect of Passive Deformation on the Lift Produced by a Rotating Hinged Wing.
Cheng, Bo
Roll, Jesse
Liu, Yun
Troolin, Daniel R.
and
Deng, Xinyan
2014.
Three-dimensional vortex wake structure of flapping wings in hovering flight.
Journal of The Royal Society Interface,
Vol. 11,
Issue. 91,
p.
20130984.
Wong, Jaime G.
and
Rival, David E.
2014.
Exploring Vortex Stability on Two-Dimensional Rotating Plates with Varying Sweepback.
Carr, Zakery R.
and
Ringuette, Matthew J.
2014.
Flow Structure of Low-Aspect-Ratio Rotating Wings from Dye Visualization.
AIAA Journal,
Vol. 52,
Issue. 5,
p.
1081.
Wojcik, Craig J.
and
Buchholz, James H. J.
2014.
Vorticity transport in the leading-edge vortex on a rotating blade.
Journal of Fluid Mechanics,
Vol. 743,
Issue. ,
p.
249.
Garmann, D. J.
and
Visbal, M. R.
2014.
Dynamics of revolving wings for various aspect ratios.
Journal of Fluid Mechanics,
Vol. 748,
Issue. ,
p.
932.
Kolomenskiy, Dmitry
Elimelech, Yossef
and
Schneider, Kai
2014.
Leading-edge vortex shedding from rotating wings.
Fluid Dynamics Research,
Vol. 46,
Issue. 3,
p.
031421.
Han, Jong-Seob
Kim, Joong-Kwan
Chang, Jo Won
and
Han, Jae-Hung
2015.
An improved quasi-steady aerodynamic model for insect wings that considers movement of the center of pressure.
Bioinspiration & Biomimetics,
Vol. 10,
Issue. 4,
p.
046014.
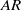 $\mathit{AR}$ ) for insect-like regimes have reported seemingly different trends in aerodynamic forces, however no detailed flow observations have been made. In this study, the effect of
$\mathit{AR}$ ) for insect-like regimes have reported seemingly different trends in aerodynamic forces, however no detailed flow observations have been made. In this study, the effect of 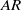 $\mathit{AR}$ and Reynolds number on the flow structures over insect-like wings is explored using a numerical model of an altered fruit fly wing revolving at a constant angular velocity. Increasing the Reynolds number for an
$\mathit{AR}$ and Reynolds number on the flow structures over insect-like wings is explored using a numerical model of an altered fruit fly wing revolving at a constant angular velocity. Increasing the Reynolds number for an 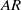 $\mathit{AR}$ of 2.91 resulted in the development of a dual leading-edge vortex (LEV) structure, however increasing
$\mathit{AR}$ of 2.91 resulted in the development of a dual leading-edge vortex (LEV) structure, however increasing 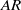 $\mathit{AR}$ at a fixed Reynolds number generated the same flow structures. This result shows that the effects of Reynolds number and
$\mathit{AR}$ at a fixed Reynolds number generated the same flow structures. This result shows that the effects of Reynolds number and 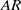 $\mathit{AR}$ are linked. We present an alternative scaling using wing span as the characteristic length to decouple the effects of Reynolds number from those of
$\mathit{AR}$ are linked. We present an alternative scaling using wing span as the characteristic length to decouple the effects of Reynolds number from those of 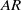 $\mathit{AR}$ . This results in a span-based Reynolds number, which can be used to independently describe the development of the LEV. Indeed, universal behaviour was found for various parameters using this scaling. The effect of
$\mathit{AR}$ . This results in a span-based Reynolds number, which can be used to independently describe the development of the LEV. Indeed, universal behaviour was found for various parameters using this scaling. The effect of 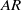 $\mathit{AR}$ on the vortex structures and aerodynamic forces was then assessed at different span-based Reynolds numbers. Scaling the flow using the wing span was found to apply when a strong spanwise velocity is present on the leeward side of the wing and therefore may prove to be useful for similar studies involving flapping or rotating wings at high angles of attack.
$\mathit{AR}$ on the vortex structures and aerodynamic forces was then assessed at different span-based Reynolds numbers. Scaling the flow using the wing span was found to apply when a strong spanwise velocity is present on the leeward side of the wing and therefore may prove to be useful for similar studies involving flapping or rotating wings at high angles of attack.
