Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T04:32:23.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Reynolds number scaling in cryogenic turbulent Rayleigh–Bénard convection in a cylindrical aspect ratio one cell

Published online by Cambridge University Press:  26 October 2017

Věra Musilová Open the ORCID record for Věra Musilová [Opens in a new window] ,
Tomáš Králík ,
Marco La Mantia Open the ORCID record for Marco La Mantia [Opens in a new window] ,
Michal Macek ,
Pavel Urban  and
Ladislav Skrbek
Věra Musilová*
Affiliation:
The Czech Academy of Sciences, Institute of Scientific Instruments, Královopolská 147, Brno, Czech Republic
Tomáš Králík
Affiliation:
The Czech Academy of Sciences, Institute of Scientific Instruments, Královopolská 147, Brno, Czech Republic
Marco La Mantia
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Prague, Czech Republic
Michal Macek
Affiliation:
The Czech Academy of Sciences, Institute of Scientific Instruments, Královopolská 147, Brno, Czech Republic
Pavel Urban
Affiliation:
The Czech Academy of Sciences, Institute of Scientific Instruments, Královopolská 147, Brno, Czech Republic
Ladislav Skrbek
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Prague, Czech Republic
*
†Email address for correspondence: vera@isibrno.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

We perform an experimental study of turbulent Rayleigh–Bénard convection up to very high Rayleigh number, 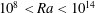$10^{8}<Ra<10^{14}$, in a cylindrical aspect ratio one cell, 30 cm in height, filled with cryogenic helium gas. We monitor temperature fluctuations in the convective flow with four small (0.2 mm) sensors positioned in pairs 1.5 cm from the sidewalls and 2.5 cm vertically apart and symmetrically around the mid-height of the cell. Based on one-point and two-point correlations of the temperature fluctuations, we determine different types of Reynolds numbers, 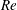$\mathit{Re}$, associated with the large-scale circulation (LSC). We observe a transition between two types of 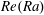$\mathit{Re}(\mathit{Ra})$ scaling around 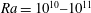$\mathit{Ra}=10^{10}{-}10^{11}$, which is accompanied by a scaling change of the skewness of the probability distribution functions (PDFs) of the temperature fluctuations. The 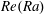$\mathit{Re}(\mathit{Ra})$ dependencies measured near the sidewall at Prandtl number 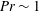$\mathit{Pr}\sim 1$ are consistent with the 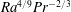$\mathit{Ra}^{4/9}\mathit{Pr}^{-2/3}$ scaling above the transition, while for 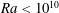$\mathit{Ra}<10^{10}$, the 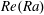$\mathit{Re}(\mathit{Ra})$ dependencies are steeper. It seems likely that this change in 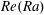$\mathit{Re}(\mathit{Ra})$ scaling is linked to the previously reported change in the Nusselt number 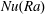$\mathit{Nu}(\mathit{Ra})$ scaling. This behaviour is in agreement with independent cryogenic laboratory experiments with 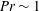$\mathit{Pr}\sim 1$, but markedly different from the 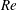$\mathit{Re}$ scaling obtained in water experiments (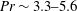$\mathit{Pr}\sim 3.3{-}5.6$). We discuss the results in comparison with different versions of the Grossmann–Lohse theory.

JFM classification

Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 721 - 744
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Brown, E. & Nikolaenko, A. 2006 The search for slow transients, and the effect of imperfect vertical alignment, in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 557, 347–367.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503.CrossRefGoogle Scholar
Belmonte, A. & Libchaber, A. 1996 Thermal signature of plumes in turbulent convection: the skewness of the derivative. Phys. Rev. E 53, 4893–4898.Google ScholarPubMed
Brown, E. & Ahlers, G. 2006a Effect of the Earth’s Coriolis force on the large-scale circulation of turbulent Rayleigh–Bénard convection. Phys. Fluids 18, 125108.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2006b Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2009 The origin of oscillations of the large-scale circulation of turbulent Rayleigh–Bénard convection. J. Fluid Mech. 638, 383–400.CrossRefGoogle Scholar
Brown, E., Funfschilling, D. & Ahlers, G. 2007 Anomalous Reynolds-number scaling in turbulent Rayleigh–Bénard convection. J. Stat. Mech. 10, P10005.Google Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.CrossRefGoogle ScholarPubMed
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X. Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.CrossRefGoogle Scholar
Cattaneo, F., Emonet, T. & Weiss, N. 2003 On the interaction between convection and magnetic fields. Astrophys. J. 588, 1183–1198.CrossRefGoogle Scholar
Chavanne, X., Chilla, F., Chabaud, B., Castaing, B. & Hebral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.CrossRefGoogle Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google ScholarPubMed
Daya, Z. A. & Ecke, R. E. 2001 Does turbulent convection feel the shape of the container? Phys. Rev. Lett. 87, 184501.CrossRefGoogle Scholar
Foroozani, N., Niemela, J. J., Armenio, V. & Sreenivasan, K. R. 2014 Influence of container shape on scaling of turbulent fluctuations in convection. Phys. Rev. E 90, 063003.Google ScholarPubMed
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.CrossRefGoogle Scholar
Funfschilling, D., Brown, E. & Ahlers, G. 2008 Torsional oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 607, 119–139.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying view. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.Google ScholarPubMed
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.CrossRefGoogle Scholar
Hartmann, D. L., Moy, L. A. & Fu, Q. 2001 Tropical convection and the energy balance at the top of the atmosphere. J. Clim. 14, 4495–4511.2.0.CO;2>CrossRefGoogle Scholar
He, X., Bodenschatz, E. & Ahlers, G. 2016 Azimuthal diffusion of the large-scale-circulation plane, and absence of significant non-Boussinesq effects, in turbulent convection near the ultimate-state transition. J. Fluid Mech. 791, R3.CrossRefGoogle Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.CrossRefGoogle Scholar
He, X., van Gils, D. P. M., Bodenschatz, E. & Ahlers, G. 2014a Logarithmic spatial variation and universal f -1 power spectra of temperature fluctuations in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 112, 174501.CrossRefGoogle ScholarPubMed
He, X., van Gils, D. P. M., Bodenschatz, E. & Ahlers, G. 2015 Reynolds numbers and the elliptic approximation near the ultimate state of turbulent Rayleigh–Bénard convection. New J. Phys. 17, 063028.CrossRefGoogle Scholar
He, X., He, G. & Tong, P. 2010 Small-scale turbulent fluctuations beyond Taylor’s frozen-flow hypothesis. Phys. Rev. E 81, 065303.Google ScholarPubMed
He, X., Shang, X. D. & Tong, P. 2014b Test of the anomalous scaling of passive temperature fluctuations in turbulent Rayleigh–Bénard convection with spatial inhomogeneity. J. Fluid Mech. 753, 104–130.CrossRefGoogle Scholar
He, G. W. & Zhang, J. B. 2006 Elliptic model for space–time correlations in turbulent shear flows. Phys. Rev. E 73, 055303.Google ScholarPubMed
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54, 34–39.CrossRefGoogle Scholar
Marshall, J. & Schott, F. 1999 Open-ocean convection: observations, theory and models. Rev. Geophys. 37, 1–64.CrossRefGoogle Scholar
McCarty, R. D.1972 Thermophysical properties of helium-4 from 2 to 1500 K with pressures to 1000 atmospheres. (Technical Note 631, National Bureau of Standards); Arp V. D. and McCarty R. D. 1998 The properties of critical helium gas (Tech. Rep., University of Oregon).CrossRefGoogle Scholar
Mitin, V. F., Kholevchuk, V. V. & Kolodych, B. P. 2011 Ge-on-GaAs film resistance thermometers: low-temperature conduction and magnetoresistance. Cryogenics 51, 68–73.CrossRefGoogle Scholar
Mitin, V. F., McDonald, P. C., Pavese, F., Boltovets, N. S., Kholevchuk, V. V., Nemish, I. Yu., Basanets, V. V., Dugaev, V. K., Sorokin, P. V., Konakova, R. V. et al. 2007 Ge-on-GaAs film resistance thermometers for cryogenic applications. Cryogenics 47, 474–482.CrossRefGoogle Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.CrossRefGoogle ScholarPubMed
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2001 The wind in confined thermal convection. J. Fluid Mech. 449, 169–178.CrossRefGoogle Scholar
Niemela, J. J. & Sreenivasan, K. R. 2003a Confined turbulent convection. J. Fluid Mech. 481, 355–384.CrossRefGoogle Scholar
Niemela, J. J. & Sreenivasan, K. R. 2003b Rayleigh-number evolution of large-scale coherent motion in turbulent convection. Europhys. Lett. 62, 829–833.CrossRefGoogle Scholar
NISTReference Fluid Thermodynamic and Transport Properties Database (REFPROP) 2000 Version 8.0, National Institute of Standards and Technology, USA.Google Scholar
Qiu, X. L. & Tong, P. 2001a Onset of coherent oscillations in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 87, 094501.CrossRefGoogle ScholarPubMed
Qiu, X. L. & Tong, P. 2001b Large-scale velocity structures in turbulent thermal convection. Phys. Rev. E 64, 036304.Google ScholarPubMed
Qiu, X. L. & Tong, P. 2002 Temperature oscillations in turbulent Rayleigh–Bénard convection. Phys. Rev. E 66, 026308.Google ScholarPubMed
Qiu, X. L., Shang, X. D., Tong, P. & Xia, K. Q. 2004 Velocity oscillations in turbulent Rayleigh–Bénard convection. Phys. Fluids 16, 412–423.CrossRefGoogle Scholar
Resagk, C., Du Puits, R., Thess, A., Dolzhanski, F. V., Grossmann, S., Araujo, F. F. & Lohse, D. 2006 Oscillations of the large scale wind in turbulent thermal convection. Phys. Fluids 18, 095105.CrossRefGoogle Scholar
Roche, P. E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12, 085014.CrossRefGoogle Scholar
Skrbek, L., Niemela, J. J., Sreenivasan, K. R. & Donnelly, R. J. 2002 Temperature structure functions in the Bolgiano regime of thermal convection. Phys. Rev. E 66, 036303.Google ScholarPubMed
Skrbek, L. & Urban, P. 2015 Has the ultimate state of turbulent thermal convection been observed? J. Fluid Mech. 785, 270–282.CrossRefGoogle Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.CrossRefGoogle Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.CrossRefGoogle Scholar
Sun, C., Xia, K. Q. & Tong, P. 2005 Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72, 026302.Google Scholar
Sun, C. & Xia, K. Q. 2005 Scaling of the Reynolds number in turbulent thermal convection. Phys. Rev. E 72, 067302.Google ScholarPubMed
Tritton, D. J. 1988 Physical Fluid Dynamics. Oxford University Press.Google Scholar
Urban, P., Hanzelka, P., Králík, T., Musilová, V., Skrbek, L. & Srnka, A. 2010 Helium cryostat for experimental study of natural turbulent convection. Rev. Sci. Instrum. 81, 085103.CrossRefGoogle ScholarPubMed
Urban, P., Hanzelka, P., Králík, T., Musilová, V., Srnka, A. & Skrbek, L. 2012 Effect of boundary layers asymmetry on heat transfer efficiency in turbulent Rayleigh–Bénard convection at very high Rayleigh numbers. Phys. Rev. Lett. 109, 154301.Google ScholarPubMed
Urban, P., Hanzelka, P., Musilová, V., Králík, T., La Mantia, M., Srnka, A. & Skrbek, L. 2014 Heat transfer in cryogenic helium gas by turbulent Rayleigh–Bénard convection in a cylindrical cell of aspect ratio 1. New J. Phys. 16, 053042.CrossRefGoogle Scholar
Urban, P., Musilová, V. & Skrbek, L. 2011 Efficiency of heat transfer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 107, 014302.CrossRefGoogle ScholarPubMed
Wei, P. & Ahlers, G. 2016 On the nature of fluctuations in turbulent Rayleigh–Bénard convection at large Prandtl numbers. J. Fluid Mech. 802, 203–244.CrossRefGoogle Scholar
Xi, H. D., Lam, S. & Xia, K. Q. 2004 From laminar plumes to organised flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.CrossRefGoogle Scholar
Xi, H. D. & Xia, K. Q. 2008 Azimuthal motion, reorientation, cessation, and reversal of the large-scale circulation in turbulent thermal convection: a comparative study in aspect ratio one and one-half geometries. Phys. Rev. E 78, 036326.Google ScholarPubMed
Xi, H. D., Zhou, S. Q., Zhou, Q., Chan, T. S. & Xia, K. Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.CrossRefGoogle ScholarPubMed
Xia, K. Q. 2013 Current trends and future directions in turbulent thermal convection. Theoret. Appl. Mech. Lett. 3, 052001.CrossRefGoogle Scholar
Xie, Y. C., Wei, P. & Xia, K. Q. 2013 Dynamics of the large-scale circulation in high-Prandtl-number turbulent thermal convection. J. Fluid Mech. 717, 322–346.CrossRefGoogle Scholar
Zhao, X. & G.-W., He 2009 Space–time correlations of fluctuating velocities in turbulent shear flows. Phys. Rev. E 79, 046316.Google ScholarPubMed
Zhou, Q., Li, C. M., Lu, Z. M. & Liu, Y. L. 2011 Experimental investigation of longitudinal space–time correlations of the velocity field in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 683, 94–111.CrossRefGoogle Scholar
Zhou, Q., Xi, H. D., Zhou, S. Q., Sun, C. & Xia, K. Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.CrossRefGoogle Scholar