Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-06T11:15:55.050Z Has data issue: false hasContentIssue false
  • English
  • Français

Shear instability in a stratified fluid when shear and stratification are not aligned

Published online by Cambridge University Press:  13 September 2011

Julien Candelier ,
Stéphane Le Dizès  and
Christophe Millet
Julien Candelier*
Affiliation:
CEA, DAM, DIF, F-91297 Arpajon, France IRPHE, CNRS and Aix–Marseille University, 49 rue F. Joliot-Curie, F-13013 Marseille, France
Stéphane Le Dizès
Affiliation:
IRPHE, CNRS and Aix–Marseille University, 49 rue F. Joliot-Curie, F-13013 Marseille, France
Christophe Millet
Affiliation:
CEA, DAM, DIF, F-91297 Arpajon, France
*
†Email address for correspondence: candelierj@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of an inclination angle of the shear with respect to the stratification on the linear properties of the shear instability is examined in the work. For this purpose, we consider a two-dimensional plane Bickley jet of width 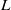and maximum velocity 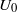in a stably stratified fluid of constant Brunt–Väisälä frequency 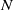in an inviscid and Boussinesq framework. The plane of the jet is assumed to be inclined with an angle 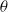with respect to the vertical direction of stratification. The stability analysis is performed using both numerical and theoretical methods for all the values of 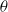and Froude number 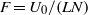. We first obtain that the most unstable mode is always a two-dimensional Kelvin–Helmholtz (KH) sinuous mode. The condition of stability based on the Richardson number 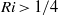, which reads here 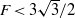, is recovered for 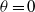. But when 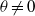, that is, when the directions of shear and stratification are not perfectly aligned, the Bickley jet is found to be unstable for all Froude numbers. We show that two modes are involved in the stability properties. 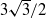We demonstrate that when is decreased below , there is a ‘jump’ from one two-dimensional sinuous mode to another. For small Froude numbers, we show that the shear instability of the inclined jet is similar to that of a horizontal jet but with a ‘horizontal’ length scale 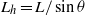. In this regime, the characteristics (oscillation frequency, growth rate, wavenumber) of the most unstable mode are found to be proportional to 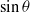. For large Froude numbers, the shear instability of the inclined jet is similar to that of a vertical jet with the same scales but with a different Froude number, 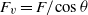. It is argued that these results could be valid for any type of shear flow.

JFM classification

Wakes/Jets: Jets Instability: Parametric instability Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 685 , 25 October 2011 , pp. 191 - 201
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Acheson, D. J. 1976 On over-reflection. J. Fluid Mech. 77, 433–472.CrossRefGoogle Scholar
2. Basak, S. & Sarkar, S. 2006 Dynamics of a stratified shear layer with horizontal shear. J. Fluid Mech. 568, 19–54.CrossRefGoogle Scholar
3. Basovich, A. Y. & Tsimring, L. S. 1984 Internal waves in a horizontally inhomogeneous flow. J. Fluid Mech. 142, 223–249.CrossRefGoogle Scholar
4. Blumen, W. 1971 Hydrostatic neutral waves in a parallel shear flow of a stratified fluid. J. Atmos. Sci. 28, 340–344.2.0.CO;2>CrossRefGoogle Scholar
5. Blumen, W. 1975 Stability of non-planar shear flow of a stratified fluid. J. Fluid Mech. 68, 177–189.CrossRefGoogle Scholar
6. Booker, J. R. & Bretherton, F. P. 1967 The critical layer for internal gravity waves in a shear flow. J. Fluid Mech. 27, 513–539.CrossRefGoogle Scholar
7. Candelier, J. 2010 Instabilités radiatives des jets et couches limites atmosphériques. PhD Thesis (in French).Google Scholar
8. Deloncle, A., Chomaz, J. M. & Billant, P. 2007 Three-dimensional stability of a horizontally sheared flow in a stably stratified fluid. J. Fluid Mech. 570, 297–305.CrossRefGoogle Scholar
9. Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
10. Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.CrossRefGoogle Scholar
11. Jacobitz, F. G. & Sarkar, S. 1998 The effect of nonvertical shear on turbulence in a stably stratified medium. Phys. Fluids 10, 1158–1168.CrossRefGoogle Scholar
12. Jacobitz, F. G. & Sarkar, S. 1999 A direct numerical study of transport and anisotropy in a stably stratified turbulent flow with uniform horizontal shear. Flow Turbul. Combust. 63, 343–360.CrossRefGoogle Scholar
13. Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21, 096602.CrossRefGoogle Scholar
14. Lindzen, R. S. & Barker, J. W. 1985 Instability and wave over-reflection in stably stratified shear flow. J. Fluid Mech. 151, 189–217.CrossRefGoogle Scholar
15. Luo, K. H. & Sandham, N. D. 1997 Instability of vortical and acoustic modes in supersonic round jets. Phys. Fluids 9, 1003–1013.CrossRefGoogle Scholar
16. Mack, L. M. 1990 On the inviscid acoustic-mode instability of supersonic shear flows. Part 1. Two-dimensional waves. Theor. Comput. Fluid Dyn. 2, 97–123.CrossRefGoogle Scholar
17. Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.CrossRefGoogle Scholar
18. Parras, L. & Le Dizès, S. 2010 Temporal instability modes of supersonic round jets. J. Fluid Mech. 660, 173–196.CrossRefGoogle Scholar
19. Riedinger, X., Le Dizès, S. & Meunier, P. 2010 Viscous stability properties of a Lamb–Oseen vortex in a stratified fluid. J. Fluid Mech. 645, 255–278.CrossRefGoogle Scholar