Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2025-01-04T11:46:17.743Z Has data issue: false hasContentIssue false
  • English
  • Français

Snowflakes in the atmospheric surface layer: observation of particle–turbulence dynamics

Published online by Cambridge University Press:  09 February 2017

Andras Nemes ,
Teja Dasari ,
Jiarong Hong ,
Michele Guala  and
Filippo Coletti
Andras Nemes
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA
Teja Dasari
Affiliation:
St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA
Jiarong Hong
Affiliation:
St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA
Michele Guala
Affiliation:
St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Civil, Environmental and Geo-Engineering, University of Minnesota, Minneapolis, MN 55455, USA
Filippo Coletti*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA
*
†Email address for correspondence: fcoletti@umn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

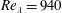We report on optical field measurements of snow settling in atmospheric turbulence at $Re_{\unicode[STIX]{x1D706}}=940$. It is found that the snowflakes exhibit hallmark features of inertial particles in turbulence. The snow motion is analysed in both Eulerian and Lagrangian frameworks by large-scale particle imaging, while sonic anemometry is used to characterize the flow field. Additionally, the snowflake size and morphology are assessed by digital in-line holography. The low volume fraction and mass loading imply a one-way interaction with the turbulent air. Acceleration probability density functions show wide exponential tails consistent with laboratory and numerical studies of homogeneous isotropic turbulence. Invoking the assumption that the particle acceleration has a stronger dependence on the Stokes number than on the specific features of the turbulence (e.g. precise Reynolds number and large-scale anisotropy), we make inferences on the snowflakes’ aerodynamic response time. In particular, we observe that their acceleration distribution is consistent with that of particles of Stokes number in the range $St=0.1{-}0.4$ based on the Kolmogorov time scale. The still-air terminal velocities estimated for the resulting range of aerodynamic response times are significantly smaller than the measured snow particle fall speed. This is interpreted as a manifestation of settling enhancement by turbulence, which is observed here for the first time in a natural setting.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Homogeneous turbulence Multiphase and Particle-laden Flows: Particle/fluid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 814 , 10 March 2017 , pp. 592 - 613
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.Google Scholar
Ayala, O., Rosa, B., Wang, L.-P. & Grabowski, W. W. 2008 Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 1. Results from direct numerical simulation. New J. Phys. 10 (7), 075015.Google Scholar
Ayyalasomayajula, S., Gylfason, A., Collins, L. R., Bodenschatz, E. & Warhaft, Z. 2006 Lagrangian measurements of inertial particle accelerations in grid generated wind tunnel turbulence. Phys. Rev. Lett. 97 (14), 144507.Google Scholar
Beals, M. J., Fugal, J. P., Shaw, R. A., Lu, J., Spuler, S. M. & Stith, J. L. 2015 Holographic measurements of inhomogeneous cloud mixing at the centimeter scale. Science 350 (6256), 87–90.Google Scholar
Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A., Musacchio, S. & Toschi, F. 2006 Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550, 349–358.Google Scholar
Bodenschatz, E., Malinowski, S. P., Shaw, R. A. & Stratmann, F. 2010 Can we understand clouds without turbulence? Science 327 (5968), 970–971.Google Scholar
Böhm, H. P. 1989 A general equation for the terminal fall speed of solid hydrometeors. J. Atmos. Sci. 46 (15), 2419–2427.Google Scholar
Brandes, E. A., Ikeda, K., Zhang, G., Schönhuber, M. & Rasmussen, R. M. 2007 A statistical and physical description of hydrometeor distributions in Colorado snowstorms using a video disdrometer. J. Appl. Meteorol. Climatol. 46 (5), 634–650.Google Scholar
Chun, J., Koch, D. L., Rani, S. L., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.CrossRefGoogle Scholar
Clift, R., Grace, J. R. & Weber, M. E. 2005 Bubbles, Drops, and Particles. Dover.Google Scholar
Clifton, A., Manes, C., Rüedi, J.-D., Guala, M. & Lehning, M. 2008 On shear-driven ventilation of snow. Boundary-Layer Meteorol. 126 (2), 249–261.Google Scholar
Davila, J. & Hunt, J. C. R. 2001 Settling of small particles near vortices and in turbulence. J. Fluid Mech. 440, 117–145.CrossRefGoogle Scholar
Dejoan, A. & Monchaux, R. 2013 Preferential concentration and settling of heavy particles in homogeneous turbulence. Phys. Fluids 25 (1), 013301.Google Scholar
Ditas, F., Shaw, R. A., Siebert, H., Simmel, M., Wehner, B. & Wiedensohler, A. 2012 Aerosols-cloud microphysics-thermodynamics-turbulence: evaluating supersaturation in a marine stratocumulus cloud. Atmos. Chem. Phys. 12 (5), 2459–2468.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.CrossRefGoogle Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52 (4), 309–329.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1992 Direct simulation of particle dispersion in a decaying isotropic turbulence. J. Fluid Mech. 242, 655–700.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1993 On the two-way interaction between homogeneous turbulence and dispersed solid particles. I. Turbulence modification. Phys. Fluids A 5 (7), 1790–1801.Google Scholar
Falkovich, G., Fouxon, A. & Stepanov, M. G. 2002 Acceleration of rain initiation by cloud turbulence. Nature 419 (6903), 151–154.Google Scholar
Ferrante, A. & Elghobashi, S. 2003 On the physical mechanisms of two-way coupling in particle-laden isotropic turbulence. Phys. Fluids 15 (2), 315–329.CrossRefGoogle Scholar
Fouras, A., Lo Jacono, D. & Hourigan, K. 2008 Target-free stereo PIV: a novel technique with inherent error estimation and improved accuracy. Exp. Fluids 44, 317–329.Google Scholar
Fugal, J. P., Schulz, T. J. & Shaw, R. A. 2009 Practical methods for automated reconstruction and characterization of particles in digital in-line holograms. Meas. Sci. Technol. 20 (7), 075501.Google Scholar
Garrett, T. J. & Yuter, S. E. 2014 Observed influence of riming, temperature, and turbulence on the fallspeed of solid precipitation. Geophys. Res. Lett. 41 (18), 6515–6522.Google Scholar
Gerashchenko, S., Sharp, N. S., Neuscamman, S. & Warhaft, Z. 2008 Lagrangian measurements of inertial particle accelerations in a turbulent boundary layer. J. Fluid Mech. 617, 255–281.CrossRefGoogle Scholar
Good, G. H., Ireland, P. J., Bewley, G. P., Bodenschatz, E., Collins, L. R. & Warhaft, Z. 2014 Settling regimes of inertial particles in isotropic turbulence. J. Fluid Mech. 759, R3.CrossRefGoogle Scholar
Grabowski, W. W. & Wang, L.-P. 2013 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45, 293–324.Google Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2010 Intermittency in the atmospheric surface layer: unresolved or slowly varying? Physica D 239 (14), 1251–1257.Google Scholar
Gulitski, G., Kholmyansky, M., Kinzelbach, W., Lüthi, B., Tsinober, A. & Yorish, S. 2007 Velocity and temperature derivatives in high-Reynolds-number turbulent flows in the atmospheric surface layer. Part 2. Accelerations and related matters. J. Fluid Mech. 589, 83–102.CrossRefGoogle Scholar
Gylfason, A., Ayyalasomayajula, S. & Warhaft, Z. 2004 Intermittency, pressure and acceleration statistics from hot-wire measurements in wind-tunnel turbulence. J. Fluid Mech. 501, 213–229.Google Scholar
Heymsfield, A. J., Bansemer, A., Schmitt, C., Twohy, C. & Poellot, M. R. 2004 Effective ice particle densities derived from aircraft data. J. Atmos. Sci. 61 (9), 982–1003.Google Scholar
Heymsfield, A. J. & Westbrook, C. D. 2010 Advances in the estimation of ice particle fall speeds using laboratory and field measurements. J. Atmos. Sci. 67 (8), 2469–2482.CrossRefGoogle Scholar
Hong, J., Toloui, M., Chamorro, L. P., Guala, M., Howard, K., Riley, S., Tucker, J. & Sotiropoulos, F. 2014 Natural snowfall reveals large-scale flow structures in the wake of a 2.5-MW wind turbine. Nat. Commun. 5, 4216.Google Scholar
Howard, K. B. & Guala, M. 2016 Upwind preview to a horizontal axis wind turbine: a wind tunnel and field-scale study. Wind Energy 19, 1371–1389.Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Met. 145 (2), 273–306.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016a The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 796, 617–658.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016b The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects. J. Fluid Mech. 796, 659–711.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.CrossRefGoogle Scholar
Katz, J. & Sheng, J. 2010 Applications of holography in fluid mechanics and particle dynamics. Annu. Rev. Fluid Mech. 42, 531–555.Google Scholar
Klewicki, J. C., Metzger, M. M., Kelner, E. & Thurlow, E. M. 1995 Viscous sublayer flow visualizations at R 𝜃≅1 500 000. Phys. Fluids 7 (4), 857–863.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13 (01), 82–85.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Locatelli, J. D. & Hobbs, P. V. 1974 Fall speeds and masses of solid precipitation particles. J. Geophys. Res. 79 (15), 2185–2197.Google Scholar
Matsuda, K., Onishi, R., Hirahara, M., Kurose, R., Takahashi, K. & Komori, S. 2014 Influence of microscale turbulent droplet clustering on radar cloud observations. J. Atmos. Sci. 71 (10), 3569–3582.CrossRefGoogle Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.CrossRefGoogle Scholar
Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8 (12), 1406.Google Scholar
Mitchell, D. L. 1996 Use of mass-and area-dimensional power laws for determining precipitation particle terminal velocities. J. Atmos. Sci. 53 (12), 1710–1723.2.0.CO;2>CrossRefGoogle Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2010 Preferential concentration of heavy particles: a Voronoï analysis. Phys. Fluids 22 (10), 103304.Google Scholar
Mordant, N., Crawford, A. M. & Bodenschatz, E. 2004 Experimental Lagrangian acceleration probability density function measurement. Physica D 193 (1), 245–251.Google Scholar
Morris, S. C., Stolpa, S. R., Slaboch, P. E. & Klewicki, J. C. 2007 Near-surface particle image velocimetry measurements in a transitionally rough-wall atmospheric boundary layer. J. Fluid Mech. 580, 319–338.Google Scholar
Ouellette, N. T., Xu, H. & Bodenschatz, E. 2006 A quantitative study of three-dimensional Lagrangian particle tracking algorithms. Exp. Fluids 40 (2), 301–313.Google Scholar
Pruppacher, H. R. & Klett, J. D. 1997 Microphysics of Clouds and Precipitation. Springer.Google Scholar
Rosa, B., Parishani, H., Ayala, O. & Wang, L.-P. 2016 Settling velocity of small inertial particles in homogeneous isotropic turbulence from high-resolution DNS. Intl J. Multiphase Flow 83, 217–231.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Salazar, J. P. L. C. & Collins, L. R. 2012 Inertial particle acceleration statistics in turbulence: effects of filtering, biased sampling, and flow topology. Phys. Fluids 24 (8), 083302.CrossRefGoogle Scholar
Shaw, R. A. 2003 Particle-turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35 (1), 183–227.Google Scholar
Shaw, R. A. & Oncley, S. P. 2001 Acceleration intermittency and enhanced collision kernels in turbulent clouds. Atmos. Res. 59, 77–87.Google Scholar
Siebert, H., Gerashchenko, S., Gylfason, A., Lehmann, K., Collins, L. R., Shaw, R. A. & Warhaft, Z. 2010 Towards understanding the role of turbulence on droplets in clouds: in situ and laboratory measurements. Atmos. Res. 97 (4), 426–437.Google Scholar
Siebert, H., Shaw, R. A., Ditas, J., Schmeissner, T., Malinowski, S. P., Bodenschatz, E. & Xu, H. 2015 High-resolution measurement of cloud microphysics and turbulence at a mountaintop station. Atmos. Meas. Tech. 8 (8), 3219–3228.Google Scholar
Squires, K. D. & Eaton, J. K. 1990 Particle response and turbulence modification in isotropic turbulence. Phys. Fluids A 2 (7), 1191–1203.Google Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids 3 (5), 1169–1178.Google Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.Google Scholar
Talapatra, S., Hong, J., McFarland, M., Nayak, A. R., Zhang, C., Katz, J., Sullivan, J., Twardowski, M., Rines, J. & Donaghay, P. 2013 Characterization of biophysical interactions in the water column using in situ digital holography. Mar. Ecol. Progress Series 473, 29–51.CrossRefGoogle Scholar
Thompson, G., Field, P. R., Rasmussen, R. M. & Hall, W. D. 2008 Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II. Implementation of a new snow parameterization. Mon. Weath. Rev. 136 (12), 5095–5115.Google Scholar
Toloui, M., Riley, S., Hong, J., Howard, K., Chamorro, L. P., Guala, M. & Tucker, J. 2014 Measurement of atmospheric boundary layer based on super-large-scale particle image velocimetry using natural snowfall. Exp. Fluids 55 (5), 1–14.Google Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.Google Scholar
Townsend, A. A. 1980 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Voth, G. A., la Porta, A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.Google Scholar
Wang, L.-P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Wang, L.-P., Wexler, A. S. & Zhou, Y. 2000 Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech. 415, 117–153.Google Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39 (6), 1096–1100.Google Scholar
Wood, A. M., Hwang, W. & Eaton, J. K. 2005 Preferential concentration of particles in homogeneous and isotropic turbulence. Intl J. Multiphase Flow 31 (10), 1220–1230.CrossRefGoogle Scholar
Yang, C. Y. & Lei, U. 1998 The role of the turbulent scales in the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 371, 179–205.CrossRefGoogle Scholar
Yang, T.-S. & Shy, S. S. 2005 Two-way interaction between solid particles and homogeneous air turbulence: particle settling rate and turbulence modification measurements. J. Fluid Mech. 526, 171–216.Google Scholar