Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T23:17:47.120Z Has data issue: false hasContentIssue false
  • English
  • Français

Speeding up thermocapillary migration of a confined bubble by wall slip

Published online by Cambridge University Press:  28 March 2014

Ying-Chih Liao ,
Yen-Ching Li ,
Yu-Chih Chang ,
Chih-Yung Huang  and
Hsien-Hung Wei
Ying-Chih Liao
Affiliation:
Department of Chemical Engineering, National Taiwan University, Taipei 106, Taiwan
Yen-Ching Li
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
Yu-Chih Chang
Affiliation:
Department of Chemical Engineering, National Taiwan University, Taipei 106, Taiwan
Chih-Yung Huang
Affiliation:
Department of Power Mechanical Engineering, National Tsing Hua University, Hsinchu 30013, Taiwan
Hsien-Hung Wei*
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
*
†Email address for correspondence: hhwei@mail.ncku.edu.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

It is usually believed that wall slip contributes small effects to macroscopic flow characteristics. Here we demonstrate that this is not the case for the thermocapillary migration of a long bubble in a slippery tube. We show that a fraction of the wall slip, with the slip length 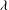$\lambda $ much smaller than the tube radius 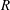$R$, can make the bubble migrate much faster than without wall slip. This speedup effect occurs in the strong-slip regime where the film thickness 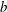$b$ is smaller than 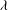$\lambda $ when the Marangoni number 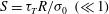$S= \tau _{T} R/\sigma _{0}~ (\ll 1)$ is below the critical value 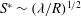$S^* \sim (\lambda /R)^{1/2}$, where 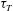$\tau _{T}$ is the driving thermal stress and 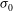$\sigma _{0}$ is the surface tension. The resulting bubble migration speed is found to be 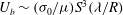$U_{b} \sim (\sigma _{0}/\mu )S^{3}(\lambda /R)$, which can be more than a hundred times faster than the no-slip result 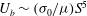$U_{b} \sim (\sigma _{0}/\mu )S^{5}$ (Wilson, J. Eng. Math., vol. 29, 1995, pp. 205–217; Mazouchi & Homsy, Phys. Fluids, vol. 12, 2000, pp. 542–549), with 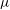$\mu $ being the fluid viscosity. The change from the fifth power law to the cubic one also indicates a transition from the no-slip state to the strong-slip state, albeit the film thickness always scales as 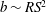$b\sim RS^{2}$. The formal lubrication analysis and numerical results confirm the above findings. Our results in different slip regimes are shown to be equivalent to those for the Bretherton problem (Liao, Li & Wei, Phys. Rev. Lett., vol. 111, 2013, 136001). Extension to polygonal tubes and connection to experiments are also made. It is found that the slight discrepancy between experiment (Lajeunesse & Homsy, Phys. Fluids, vol. 15, 2003, pp. 308–314) and theory (Mazouchi & Homsy, Phys. Fluids, vol. 13, 2001, pp. 1594–1600) can be interpreted by including wall slip effects.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Lubrication theory Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 746 , 10 May 2014 , pp. 31 - 52
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baroud, C. N., Delville, J.-P., Gallaire, F. & Wunenburger, R. 2007 Thermocapillary valve for droplet production and sorting. Phys. Rev. E 75, 046302.Google Scholar
Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10, 166–188.Google Scholar
Brochard-Wyart, F., Debrégeas, G. & de Gennes, P. G. 1996 Spreading of viscous droplets on a non-viscous liquid. Colloid Polym. Sci. 274, 70–72.Google Scholar
Brzoska, J. B., Brochard-Wyart, F. & Rondelez, F. 1993 Motions of droplets on hydrophobic model surfaces induced by thermal gradients. Langmuir 9, 2220–2224.Google Scholar
Choi, C.-H. & Kim, C.-J. 2006 Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface. Phys. Rev. Lett. 96, 066001.Google Scholar
Craig, V. S. J., Neto, C. & Williams, D. R. M. 2001 Shear-dependent boundary slip in an aqueous Newtonian liquid. Phys. Rev. Lett. 87, 054504.Google Scholar
Darhuber, A. A., Valentino, J. P., Troian, S. M. & Wagner, S. 2003 Thermocapillary actuation of droplets on chemically patterned surfaces by programmable microheater arrays. J. Microelectromech. Syst. 12, 873–879.Google Scholar
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.Google Scholar
de Gennes, P. G., Brochard-Wyart, F. & Quéré, D. 2003 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Gomba, J. M. & Homsy, G. M. 2010 Regimes of thermocapillary migration of droplets under partial wetting conditions. J. Fluid Mech. 647, 125–142.Google Scholar
Homsy, G. M. 1987 Viscous fingering in porous media. Annu. Rev. Fluid Mech. 19, 271–311.Google Scholar
Hu, G.-H. 2005 Linear stability of ultrathin slipping films with insoluble surfactant. Phys. Fluids 17, 088105.Google Scholar
Jiao, Z., Huang, X., Nguyen, N.-T. & Abgrall, P. 2008 Thermocapillary actuation of a droplet in a planar microchannel. Microfluid. Nanofluid. 5, 205–214.Google Scholar
Karapetsas, G., Sahu, K. C. & Matar, O. K. 2013 Effect of contact line dynamics on the thermocapillary motion of a droplet on an inclined plate. Langmuir 29, 8892–8906.Google Scholar
Kargupta, K., Sharma, A. & Khanna, R. 2004 Instability, dynamics and morphology of thin slipping film. Langmuir 20, 244–253.Google Scholar
Lajeunesse, E. & Homsy, G. M. 2003 Thermocapillary migration of long bubbles in polygonal tubes. II. Experiments. Phys. Fluids 15, 308–314.Google Scholar
Lauga, E., Brenner, M. P. & Stone, H. A. 2007 Microfluidics: the no-slip boundary condition. In Springer Handbook of Experimental Fluid Mechanics, pp. 1219–1240. Springer.Google Scholar
Li, Y.-C., Liao, Y.-C., Wen, T.-C. & Wei, H.-H. 2014 Breakdown of the Bretherton law due to wall slippage. J. Fluid Mech. 741, 200–227.Google Scholar
Liao, Y.-C., Li, Y.-C. & Wei, H.-H. 2013 Drastic changes in interfacial hydrodynamics due to wall slippage: slip-intensified film thinning, drop spreading, and capillary instability. Phys. Rev. Lett. 111, 136001.Google Scholar
Mazouchi, A. & Homsy, G. M. 2000 Thermocapillary migration of long bubbles in cylindrical capillary tubes. Phys. Fluids 12, 542–549.Google Scholar
Mazouchi, A. & Homsy, G. M. 2001 Thermocapillary migration of long bubbles in polygonal tubes. I. Theory. Phys. Fluids 13, 1594–1600.Google Scholar
Münch, A. 2005 Dewetting rates of thin liquid films. J. Phys.: Condens. Matter 17, S309–S318.Google Scholar
Münch, A. & Wagner, B. 2005 Contact-line instability of dewetting thin films. Physica D 209, 178–190.Google Scholar
Münch, A., Wagner, B. & Witelski, T. P. 2005 Lubrication models with small to large slip lengths. J. Engng Math. 53, 359–383.Google Scholar
Navier, C. L. M. H. 1823 Mémoire sur les lois du mouvement des fluids. Mém. Présentés par Divers Savants Acad. Sci. Inst. Fr. 6, 389–440.Google Scholar
Nguyen, H.-B. & Chen, J.-C. 2010 A numerical study of thermocapillary migration of a small liquid droplet on a horizontal solid surface. Phys. Fluids 22, 062102.Google Scholar
Pratap, V., Moumen, N. & Subramanian, R. S. 2008 Thermocapillary motion of a liquid drop on a horizontal solid surface. Langmuir 24, 5185–5193.Google Scholar
Saffman, P. G. & Taylor, G. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245, 312–329.Google Scholar
Selva, B., Miralles, V., Cantat, I. & Jullien, M.-C. 2010 Thermocapillary actuation by optimised resistor pattern: bubbles and droplets, displacing, switching and trapping. Lab on a Chip 10, 1835–1840.Google Scholar
Sharma, A. & Kargupta, K. 2003 Instability and dynamics of thin slipping films. Appl. Phys. Lett. 83, 3549–3551.Google Scholar
Slattery, J. C. 1974 Interfacial effects in the entrapment and displacement of residual oil. AIChE J. 20, 1145–1154.Google Scholar
Smith, M. K. 1995 Thermocapillary migration of a two-dimensional liquid droplet on a solid surface. J. Fluid Mech. 294, 209–230.Google Scholar
Stone, H. A. 2010 Interfaces: in fluid mechanics and across disciplines. J. Fluid Mech. 645, 1–25.Google Scholar
Subramanian, R. S. 1981 Slow migration of a gas bubble in a thermal gradient. AIChE J. 27, 646–654.Google Scholar
Tyrrell, J. W. G. & Attard, P. 2001 Images of nanobubbles on hydrophobic surfaces and their interactions. Phys. Rev. Lett. 87, 176104.Google Scholar
Wilson, S. K. 1993 The steady thermocapillary-driven motion of a large droplet in a closed tube. Phys. Fluids A 5, 2064–2066.Google Scholar
Wilson, S. K. 1995 The effect of an axial temperature gradient on the steady motion of a large droplet in a tube. J. Engng Math. 29, 205–217.Google Scholar
Young, N. O., Goldstein, J. S. & Block, M. J. 1959 The motion of bubbles in a vertical temperature gradient. J. Fluid Mech. 6, 350–356.Google Scholar