Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-18T21:32:39.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Threshold condition for spray formation by Faraday instability

Published online by Cambridge University Press:  20 October 2014

Yikai Li  and
Akira Umemura
Yikai Li*
Affiliation:
Department of Aerospace Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8603, Japan
Akira Umemura
Affiliation:
Department of Aerospace Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8603, Japan
*
†Email address for correspondence: li.yikai@f.mbox.nagoya-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

A vertically vibrating liquid layer produces liquid ligaments that disintegrate to form a spray with drops of a controllable size. Previous experimental investigations of ultrasonic atomisation have shown that when such a spray forms, there exists a predominant surface-wave mode from which drops are generated with a mean diameter that follows Lang’s equation. In this paper, we determined this predominant surface-wave mode physically and, by utilising the coupled level-set and volume-of-fluid method, we numerically studied the threshold condition for spray formation based on a cell model of the predominant surface wavelength that excludes the effects of the container walls. We defined a condition whereby the broken drop holds a zero area-averaged vertical velocity in the laboratory reference frame as the criterion for the formation of a spray. 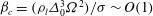The results of our calculations indicated that the onset of a spray occurs in the subharmonic unstable region for a threshold dimensionless forcing strength ${\it\beta}_{c}=({\it\rho}_{l}{\it\Delta}_{0}^{3}{\it\Omega}^{2})/{\it\sigma}\sim O(1)$, where 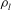${\it\rho}_{l}$ and ${\it\sigma}$ denote the liquid density and surface tension coefficient, respectively, 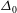${\it\Delta}_{0}$ is the forcing displacement amplitude and 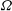${\it\Omega}$ is the forcing angular frequency. Spray formation due to the Faraday instability can be considered as a process whereby the liquid layer absorbs energy from the inertial force, and releases it by producing drops that leave the surface of the liquid layer. We demonstrated that for a deep liquid layer, the threshold condition for the formation of a spray is determined only by the forcing strength, and is independent of the initial conditions of the liquid surface.

JFM classification

Drops and Bubbles: Aerosols/atomization Multiphase and Particle-laden Flows: Gas/liquid flow Waves/Free-surface Flows: Faraday waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 759 , 25 November 2014 , pp. 73 - 103
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aranson, I. S. & Kramer, L. 2002 The world of the complex Ginzburg–Landau equation. Rev. Mod. Phys. 74, 99–161.Google Scholar
Barreras, F., Amaveda, H. & Lozano, A. 2002 Transient high-frequency ultrasonic water atomization. Exp. Fluids 33, 405–413.Google Scholar
Benjamin, T. B. & Ursell, F. 1954 The stability of the plane free surface of a liquid in vertical periodic motion. Proc. R. Soc. Lond. A 225, 505–515.Google Scholar
Boguslav, Y. Y. & Eknadios, O. K. 1969 Physical mechanism of acoustic atomization of a liquid. Sov. Phys. Acoust. 15, 14–21.Google Scholar
Brackbill, J., Kothe, D. B. & Zemach, C. 1992 A continuum method for modeling surface tension. J. Comput. Phys. 100, 335–354.CrossRefGoogle Scholar
Chen, P. & Viñals, J. 1999 Amplitude equation and pattern selection in Faraday waves. Phys. Rev. E 60, 559–570.CrossRefGoogle ScholarPubMed
Donnelly, T., Hogan, J., Mugler, A., Schommer, N., Schubmehl, M., Bernoff, A. J. & Forrest, B. 2004 An experimental study of micron-scale droplet aerosols produced via ultrasonic atomization. Phys. Fluids 16, 2843–2851.Google Scholar
Eisenmenger, M. 1959 Dynamic properties of the surface tension of water and aqueous solutions of surface active agents with standing capillary waves in the frequency range from $10\ \text{kc s}^{-1}$ to $1.5\ \text{Mc s}^{-1}$ . Acustica 9, 327–340.Google Scholar
Faraday, M. 1831 On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Phil. Trans. R. Soc. Lond. 121, 299–340.Google Scholar
Goodridge, C. L., Shi, W. T., Hentschel, H. & Lathrop, D. P. 1997 Viscous effects in droplet-ejecting capillary waves. Phys. Rev. E 56, 472–475.Google Scholar
Goodridge, C. L., Shi, W. T. & Lathrop, D. P. 1996 Threshold dynamics of singular gravity–capillary waves. Phys. Rev. Lett. 76, 1824–1827.Google Scholar
Harlow, F. H. & Welch, J. E. 1965 Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 8, 2182–2189.Google Scholar
James, A. J., Smith, M. K. & Glezer, A. 2003a Vibration-induced drop atomization and the numerical simulation of low-frequency single-droplet ejection. J. Fluid Mech. 476, 29–62.Google Scholar
James, A. J., Vukasinovic, B., Smith, M. K. & Glezer, A. 2003b Vibration-induced drop atomization and bursting. J. Fluid Mech. 476, 1–28.Google Scholar
Kelvin, L. 1871 Hydrokinetic solutions and observations. Phil. Mag. 42, 362–377.Google Scholar
Kumar, K. & Tuckerman, L. S. 1994 Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68.Google Scholar
Lang, R. J. 1962 Ultrasonic atomization of liquids. J. Acoust. Soc. Am. 34, 6–9.Google Scholar
Li, Y. & Umemura, A. 2014 Two-dimensional numerical investigation on the dynamics of ligament formation by Faraday instability. Intl J. Multiphase Flow 60, 64–75.Google Scholar
McCallion, O., Taylor, K., Thomas, M. & Taylor, A. 1995 Nebulization of fluids of different physicochemical properties with air-jet and ultrasonic nebulizers. Pharmaceut. Res. 12, 1682–1688.Google Scholar
Majumder, M., Rendall, C., Li, M., Behabtu, N., Eukel, J. A., Hauge, R., Schmidt, H. & Pasquali, M. 2010 Insights into the physics of spray coating of SWNT films. Chem. Engng Sci. 65, 2000–2008.Google Scholar
Millington, B., Whipple, V. & Pollet, B. 2011 A novel method for preparing proton exchange membrane fuel cell electrodes by the ultrasonic-spray technique. J. Power Sources 196, 8500–8508.Google Scholar
Müller, H. W. 1994 Model equations for two-dimensional quasipatterns. Phys. Rev. E 49, 1273–1277.CrossRefGoogle ScholarPubMed
Nichols, B., Hirt, C. & Hotchkiss, R.1980 SOLA-VOF: a solution algorithm for transient fluid flow with multiple free boundaries. Tech. Rep. 8355. Los Alamos Scientific Laboratory, NM, USA.Google Scholar
Peskin, R. L. & Raco, R. J. 1963 Ultrasonic atomization of liquids. J. Acoust. Soc. Am. 35, 1378–1381.Google Scholar
Puthenveettil, B. A. & Hopfinger, E. J. 2009 Evolution and breaking of parametrically forced capillary waves in a circular cylinder. J. Fluid Mech. 633, 355–379.Google Scholar
Rajan, R. & Pandit, A. 2001 Correlations to predict droplet size in ultrasonic atomisation. Ultrasonics 39, 235–255.Google Scholar
Sato, M., Matsuura, K. & Fujii, T. 2001 Ethanol separation from ethanol–water solution by ultrasonic atomization and its proposed mechanism based on parametric decay instability of capillary wave. J. Chem. Phys. 114, 2382–2386.Google Scholar
Schulkes, R. 1994 The evolution and bifurcation of a pendant drop. J. Fluid Mech. 278, 83–100.Google Scholar
Stone, H. A. & Leal, L. G. 1989a The influence of initial deformation on drop breakup in subcritical time-dependent flows at low Reynolds numbers. J. Fluid Mech. 206, 223–263.Google Scholar
Stone, H. A. & Leal, L. G. 1989b Relaxation and breakup of an initially extended drop in an otherwise quiescent fluid. J. Fluid Mech. 198, 399–427.Google Scholar
Ubal, S., Giavedoni, M. D. & Saita, F. A. 2003 A numerical analysis of the influence of the liquid depth on two-dimensional Faraday waves. Phys. Fluids 15, 3099–3113.Google Scholar
Umemura, A. 2011 Self-destabilizing mechanism of a laminar inviscid liquid jet issuing from a circular nozzle. Phys. Rev. E 83, 046307.CrossRefGoogle ScholarPubMed
Umemura, A., Kawanabe, S., Suzuki, S. & Osaka, J. 2011 Two-valued breakup length of a water jet issuing from a finite-length nozzle under normal gravity. Phys. Rev. E 84, 036309.Google Scholar
Van der Pijl, S., Segal, A., Vuik, C. & Wesseling, P. 2005 A mass-conserving level-set method for modelling of multi-phase flows. Intl J. Numer. Meth. Fluids 47, 339–361.Google Scholar
Vukasinovic, B., Smith, M. K. & Glezer, A. 2007 Mechanisms of free-surface breakup in vibration-induced liquid atomization. Phys. Fluids 19, 012104.Google Scholar
Westra, M. T., Binks, D. G. & Van der Water, W. 2003 Patterns of Faraday waves. J. Fluid Mech. 496, 1–32.Google Scholar
Wright, J., Yon, S. & Pozrikidis, C. 2000 Numerical studies of two-dimensional Faraday oscillations of inviscid fluids. J. Fluid Mech. 402, 1–32.Google Scholar
Yule, A. & Suleimani, Y. A. 2000 On droplet formation from capillary waves on a vibrating surface. Proc. R. Soc. Lond. A 456, 1069–1085.Google Scholar
Zhang, W. & Viñals, J. 1997 Pattern formation in weakly damped parametric surface waves. Phys. Rev. E 336, 301–330.Google Scholar