1. Introduction
Multi-phase flows are omnipresent in science and technology. From micro-droplets coalescing in clouds to solidification or melting of alloys and diesel droplets evaporation and subsequent combustion, all involve multiple interacting phases and moving interfaces. This ubiquity fuelled wide efforts focused on the development of predictive mathematical models and numerical tools for multi-phase flows. While significant attention has been focused on sharp interface methods requiring efficient tracking of the evolving and deforming interfaces, and imposing jump conditions (Scardovelli & Zaleski Reference Scardovelli and Zaleski1999; Sethian & Smereka Reference Sethian and Smereka2003; Prosperetti & Tryggvason Reference Prosperetti and Tryggvason2009; Popinet Reference Popinet2018), the ever-growing range of temperatures and pressures involved in typical systems of interest is making thermodynamic consistency of the computational models essential. For instance, dramatically different thermodynamic regimes are encountered in diesel engines during the compression phase, in aeronautical engines during take-off, while most rocket engines operate in trans- and super-critical regimes, where the interface thickness becomes comparable to the flow scales. Nucleation and cavitation are yet another example, where the sharp interface limit does not hold and modifications to the classical nucleation theory (Debenedetti Reference Debenedetti1997), related to curvature-dependence of the surface tension, are required. In such cases, an accurate account of the non-ideality of the fluid, including a finite interface thickness, is crucial for predictive numerical simulations of the flow physics. At a macroscopic level, a prime example for thermodynamics of non-ideal fluids is the second-gradient theory, first introduced by van der Waals for single-component fluids (van der Waals Reference van der Waals1894), leading to the Navier–Stokes equations supplemented with the Korteweg stress tensor (Korteweg Reference Korteweg1901), and is a starting point for numerical methods known as the diffuse interface approach (Anderson, McFadden & Wheeler Reference Anderson, McFadden and Wheeler1998). Additionally, extension of the Boltzmann equation to dense gases within the Enskog hard-sphere collision model (Enskog Reference Enskog1921) and the Vlasov mean-field approximation (Vlasov Reference Vlasov1961) provides a kinetic-theory basis for the dynamics of a non-ideal fluid (Chapman & Cowling Reference Chapman and Cowling1939).
Since the pioneering work of Shan & Chen (Reference Shan and Chen1993), the lattice Boltzmann method (LBM) has gained popularity as a viable numerical tool targeting the hydrodynamic regime of multi-phase flows. Despite their popularity and wide usage, most multi-phase models for LBM, apart from a limited number of studies (He, Shan & Doolen Reference He, Shan and Doolen1998; Martys Reference Martys2001, Reference Martys1999, Reference Martys2006; He & Doolen Reference He and Doolen2002), lack a clear kinetic-theory thermodynamic framework and/or well-defined target continuum thermodynamics. For instance, despite active development and research, the so-called pseudo-potential lattice Boltzmann models lack a clear and consistent continuous kinetic model, scaling law recovering the full target macroscopic system and continuum level free energy functional (Sbragaglia et al. Reference Sbragaglia, Chen, Shan and Succi2009). Thorough analyses of the bulk thermodynamic and interface properties of the models (especially near the critical state) are also very scarce. Furthermore, ever since their inception, such models have continuously struggled with larger density ratio simulations achieving at best, via different strategies, ratios of the order of ![]() $10^3$, as reflected by a number of recent reviews (Chen et al. Reference Chen, Kang, Mu, He and Tao2014; Li et al. Reference Li, Luo, Kang, He, Chen and Liu2016).
$10^3$, as reflected by a number of recent reviews (Chen et al. Reference Chen, Kang, Mu, He and Tao2014; Li et al. Reference Li, Luo, Kang, He, Chen and Liu2016).
In this paper, we revisit the construction of the lattice Boltzmann model for isothermal two-phase flows. We propose a flexible kinetic framework for dense fluids with non-ideal equations of states. Using the lattice Boltzmann method discretization strategy, and under proper scaling, the model is shown to recover the full Navier–Stokes–Korteweg system of equations. Through a detailed study of the thermodynamic properties, the model is shown to be well posed and convergent to the capillary fluid thermodynamics. The well-posedness of the model and proper consideration of the proposed scaling is shown to guarantee recovery of the hydrodynamic-scale dynamics both at very large density ratio and near critical point.
The outline is as follows: we begin in § 2.1 with a summary of the second-gradient theory due to van der Waals (Reference van der Waals1894) and Korteweg (Reference Korteweg1901). In § 2.2, following a more microscopic approach, we consider a class of kinetic models suitable for a non-ideal fluid. We proceed in § 2.3 with a scaling assumption of small flow velocity increments which leads to a lattice Bhatnagar–Gross–Krook (LBGK) equation with a new realization of the non-local force that guarantees consistency with Korteweg's stress.
Thermodynamics of the LBGK model is validated in § 3. In §§ 3.1 and 3.2, we demonstrate convergence of vapour–liquid coexistence to the thermodynamic Maxwell construction via the principle of corresponding states (Guggenheim Reference Guggenheim1945), independently of the equation of state and for liquid–vapour density ratios up to at least ![]() ${\sim }10^{11}$. The remainder of the paper is based on the van der Waals equation of state. In § 3.3, we show that the surface tension in the present LBGK model obeys a temperature scaling in excellent agreement with the theory. After verifying that the proposed model allows for choosing surface tension independently of the density ratio in § 3.4, we show in § 3.5 that it is also consistent with Gibbs’ theory of dividing surfaces (Gibbs Reference Gibbs1874). Simulations presented in § 3.5 reveal a generalized Laplace law and uncover the effect of curvature on the surface tension, in agreement with the theory by Tolman (Reference Tolman1949). Finally, in § 3.6, we show that the interface width scales with the temperature in accord with van der Waals theory.
${\sim }10^{11}$. The remainder of the paper is based on the van der Waals equation of state. In § 3.3, we show that the surface tension in the present LBGK model obeys a temperature scaling in excellent agreement with the theory. After verifying that the proposed model allows for choosing surface tension independently of the density ratio in § 3.4, we show in § 3.5 that it is also consistent with Gibbs’ theory of dividing surfaces (Gibbs Reference Gibbs1874). Simulations presented in § 3.5 reveal a generalized Laplace law and uncover the effect of curvature on the surface tension, in agreement with the theory by Tolman (Reference Tolman1949). Finally, in § 3.6, we show that the interface width scales with the temperature in accord with van der Waals theory.
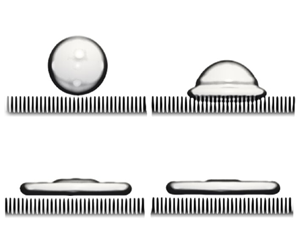
We turn to probing hydrodynamic features of our model in § 4. In § 4.1, we demonstrate that it correctly implements the jump condition for the stresses at the liquid–vapour interface in the simulation of a layered Poiseuille flow. In § 4.2, Galilean invariance is demonstrated by measuring the dissipation of normal modes in a moving reference frame. The viscosity–capillarity coupling is probed in § 4.3 by measuring the frequency of higher-order capillary waves, in excellent agreement with Rayleigh's theory (Rayleigh Reference Rayleigh1879). We also demonstrate that the damping rate of a capillary wave agrees with the analytical solution. Validation of bulk properties is concluded by measuring the isothermal speed of sound in § 4.4, where excellent comparison to the theoretical prediction is demonstrated for large density ratios. In § 4.5, the model is extended to the simulation of a fluid–solid interface, and is validated by demonstrating the Young–Laplace law and a liquid column motion in a channel with non-uniform wettability. In § 5, the model is used to simulate water impact on textured superhydrophobic surfaces and the coalescence of mercury droplets, to demonstrate its ability to handle simulations at extremely high density ratios. Conclusions are drawn in § 6.
2. Model for two-phase flows
2.1. Second-gradient theory: Korteweg's stress and capillary fluid equations
In the second-gradient theory as introduced by van der Waals (Reference van der Waals1894), free energy per unit volume is expressed as
where ![]() $\mathcal {A}$ is the bulk free energy per unit volume,
$\mathcal {A}$ is the bulk free energy per unit volume, ![]() $\rho$ is the density and
$\rho$ is the density and ![]() $\kappa$ is the capillary coefficient. The second term represents the interface energy while the bulk free energy is solely a function of the local density and temperature (Cahn & Hilliard Reference Cahn and Hilliard1958; Giovangigli Reference Giovangigli2020). The equilibrium state of the corresponding system is obtained by minimizing the free energy in a given volume under the constraint of constant total mass, leading to the stress tensor (Anderson et al. Reference Anderson, McFadden and Wheeler1998),
$\kappa$ is the capillary coefficient. The second term represents the interface energy while the bulk free energy is solely a function of the local density and temperature (Cahn & Hilliard Reference Cahn and Hilliard1958; Giovangigli Reference Giovangigli2020). The equilibrium state of the corresponding system is obtained by minimizing the free energy in a given volume under the constraint of constant total mass, leading to the stress tensor (Anderson et al. Reference Anderson, McFadden and Wheeler1998),
where ![]() $\boldsymbol{\mathsf{I}}$ is unit tensor and
$\boldsymbol{\mathsf{I}}$ is unit tensor and ![]() $\mathcal {L}$ is the Lagrange function,
$\mathcal {L}$ is the Lagrange function,
and ![]() $\lambda$ is the Lagrange multiplier for the mass constraint, or chemical potential,
$\lambda$ is the Lagrange multiplier for the mass constraint, or chemical potential,
where ![]() $\boldsymbol {\nabla }^2$ is the Laplace operator. This in turn leads to the following Korteweg's stress tensor (Korteweg Reference Korteweg1901):
$\boldsymbol {\nabla }^2$ is the Laplace operator. This in turn leads to the following Korteweg's stress tensor (Korteweg Reference Korteweg1901):
where
is the thermodynamic pressure, or equation of state. From the local balance equations for mass and momentum, one obtains the macroscopic governing laws for an isothermal capillary fluid:
where ![]() $\boldsymbol {u}$ is the fluid velocity and the stress tensor
$\boldsymbol {u}$ is the fluid velocity and the stress tensor ![]() $\boldsymbol{\mathsf{T}}$ is
$\boldsymbol{\mathsf{T}}$ is
The Navier–Stokes viscous stress tensor reads
where ![]() $\boldsymbol{\mathsf{S}}$ is the trace-free rate-of-strain tensor,
$\boldsymbol{\mathsf{S}}$ is the trace-free rate-of-strain tensor,
and ![]() $\mu$ and
$\mu$ and ![]() $\eta$ are the dynamic and the bulk viscosity, respectively.
$\eta$ are the dynamic and the bulk viscosity, respectively.
The momentum balance equation in (2.8) can be recast in the following form:
where Korteweg's force ![]() $\boldsymbol {F}_{K}$ is the divergence of the Korteweg pressure tensor,
$\boldsymbol {F}_{K}$ is the divergence of the Korteweg pressure tensor,
The latter can be written in the following form:
where we have introduced a reference pressure ![]() $P_0$. Navier–Stokes momentum equations with Korteweg's force in (2.14) shall be a target for reconstruction by a suitable kinetic model.
$P_0$. Navier–Stokes momentum equations with Korteweg's force in (2.14) shall be a target for reconstruction by a suitable kinetic model.
2.2. Kinetic model for non-ideal fluid
To introduce a kinetic model for non-ideal fluid, we begin with the first Bogolioubov–Born–Green–Kirkwood–Yvon (BBGKY) equation,
where ![]() $f(\boldsymbol {r},\boldsymbol {v},t)$ and
$f(\boldsymbol {r},\boldsymbol {v},t)$ and ![]() $f_{2}(\boldsymbol {r},\boldsymbol {v},\boldsymbol {r}_1,\boldsymbol {v}_1,t)$ are the one- and the two-particle distribution functions, respectively,
$f_{2}(\boldsymbol {r},\boldsymbol {v},\boldsymbol {r}_1,\boldsymbol {v}_1,t)$ are the one- and the two-particle distribution functions, respectively, ![]() $\boldsymbol {r}$,
$\boldsymbol {r}$, ![]() $\boldsymbol {r}_1$ and
$\boldsymbol {r}_1$ and ![]() $\boldsymbol {v}$,
$\boldsymbol {v}$, ![]() $\boldsymbol {v}_1$ are particles’ position and velocity, while
$\boldsymbol {v}_1$ are particles’ position and velocity, while ![]() $V$ is a potential of a pair interaction. The local equilibrium state is defined by the Maxwellian
$V$ is a potential of a pair interaction. The local equilibrium state is defined by the Maxwellian ![]() $f^{eq}$ at constant temperature
$f^{eq}$ at constant temperature ![]() $T$, parametrized by the local values of density
$T$, parametrized by the local values of density ![]() $\rho$ and flow velocity
$\rho$ and flow velocity ![]() $\boldsymbol {u}$,
$\boldsymbol {u}$,
where ![]() $R$ is the gas constant. Furthermore, let us introduce a projector
$R$ is the gas constant. Furthermore, let us introduce a projector ![]() $\mathcal {K}$ onto local equilibrium at constant temperature (Gorban & Karlin Reference Gorban and Karlin2005),
$\mathcal {K}$ onto local equilibrium at constant temperature (Gorban & Karlin Reference Gorban and Karlin2005),
The projector property, ![]() $\mathcal {K}^2=\mathcal {K}$, can be verified by a direct computation. With the projector in (2.17), the interaction term in (2.15) is split into two parts by writing an identity,
$\mathcal {K}^2=\mathcal {K}$, can be verified by a direct computation. With the projector in (2.17), the interaction term in (2.15) is split into two parts by writing an identity,
The first term,
satisfies the local conservation of both mass and momentum,
It is conventional to model the locally conserving part of the interaction with a single relaxation time Bhatnagar–Gross–Krook (BGK) approximation,
where the relaxation time ![]() $\tau$ is a free parameter. The second term in the identity of (2.18),
$\tau$ is a free parameter. The second term in the identity of (2.18),
satisfies the local mass but not the local momentum conservation. Indeed, after integration by part in the velocity ![]() $\boldsymbol {v}$ and neglecting boundary integrals, we arrive at
$\boldsymbol {v}$ and neglecting boundary integrals, we arrive at
where the force ![]() $\boldsymbol {F}_{nloc}$ reads
$\boldsymbol {F}_{nloc}$ reads
Collecting the BGK approximation together with the non-local contribution, a generic kinetic model may be written as
Evaluation of the force in (2.24) requires us to specify the particles interaction. It is customary to invoke the Enskog–Vlasov model (Enskog Reference Enskog1921; Vlasov Reference Vlasov1961), where both hard-sphere collisions and a weak long-range attraction potential contribute to a non-local momentum transfer. For the hard-sphere Enskog part, a de-localization of the collision is responsible for a non-vanishing contribution of momentum transfer through the distance between the centres of the spheres upon their impact while the Vlasov approximation contributes non-locally to the momentum transfer from a distributed mean-field force. Evaluation of both the Enskog and Vlasov contributions to the force in (2.24) proceeds along familiar lines (Chapman & Cowling Reference Chapman and Cowling1939; He et al. Reference He, Shan and Doolen1998; He & Doolen Reference He and Doolen2002; Martys Reference Martys2006) and is reported in Appendices A and B for completeness,
The first term is the lowest-order contribution of the collisional momentum transfer from the Enskog hard-sphere model,
Here ![]() $b=4v_{HS}$, with
$b=4v_{HS}$, with ![]() $v_{HS}=\mathcal {V}_{HS}/m$ the specific volume of a hard sphere of diameter
$v_{HS}=\mathcal {V}_{HS}/m$ the specific volume of a hard sphere of diameter ![]() $d$ and mass
$d$ and mass ![]() $m$, while
$m$, while ![]() $\mathcal {V}_{HS}={\rm \pi} d^3/6$ is the volume of the sphere. Moreover,
$\mathcal {V}_{HS}={\rm \pi} d^3/6$ is the volume of the sphere. Moreover, ![]() $\chi$ is the equilibrium two-particle correlation function, evaluated at the local density reduced by the specific volume of the hard sphere,
$\chi$ is the equilibrium two-particle correlation function, evaluated at the local density reduced by the specific volume of the hard sphere, ![]() $\chi =\chi (b\rho (\boldsymbol {r},t))$. To the lowest order,
$\chi =\chi (b\rho (\boldsymbol {r},t))$. To the lowest order, ![]() $\chi =1+(5/8)b\rho +O((b\rho )^2)$, cf. Chapman & Cowling (Reference Chapman and Cowling1939). The second term in (2.26) is the contribution of a long-range attraction potential
$\chi =1+(5/8)b\rho +O((b\rho )^2)$, cf. Chapman & Cowling (Reference Chapman and Cowling1939). The second term in (2.26) is the contribution of a long-range attraction potential ![]() $V$ in the mean field Vlasov approximation. To third order in the gradient of density,
$V$ in the mean field Vlasov approximation. To third order in the gradient of density,
where parameters ![]() $a$ and
$a$ and ![]() $\kappa$ are
$\kappa$ are
Thus, with the approximations specified, the non-local force in (2.26) becomes
where the reference ideal gas pressure ![]() $P_0$ is provided by the local Maxwellian in (2.16),
$P_0$ is provided by the local Maxwellian in (2.16),
while the equation of state of the Enskog–Vlasov gas is of van der Waals type,
This allows us to extend the Enskog–Vlasov kinetic model, and a phenomenological equation of state ![]() $P$ in (2.6) can be used instead of
$P$ in (2.6) can be used instead of ![]() $P_{EV}$ in (2.33). Moreover, the reference pressure
$P_{EV}$ in (2.33). Moreover, the reference pressure ![]() $P_0$ can be made selective by rescaling the local equilibrium,
$P_0$ can be made selective by rescaling the local equilibrium,
where ![]() $D$ is the space dimension. While the Enskog–Vlasov partition above corresponds to selecting
$D$ is the space dimension. While the Enskog–Vlasov partition above corresponds to selecting ![]() $P_0 = \rho R T$, an alternative is provided by Reyhanian, Dorschner & Karlin (Reference Reyhanian, Dorschner and Karlin2020), where
$P_0 = \rho R T$, an alternative is provided by Reyhanian, Dorschner & Karlin (Reference Reyhanian, Dorschner and Karlin2020), where ![]() $P_0 = P$ is chosen. Another construction was proposed (Martys Reference Martys1999, Reference Martys2001) where all contributions to the pressure tensor are introduced with the local attractor, rescaling temperature and introducing a velocity shift to match the targeted system of moments. Using the rescaled equilibria in (2.34), a family of kinetic models parametrized by the reference pressure reads
$P_0 = P$ is chosen. Another construction was proposed (Martys Reference Martys1999, Reference Martys2001) where all contributions to the pressure tensor are introduced with the local attractor, rescaling temperature and introducing a velocity shift to match the targeted system of moments. Using the rescaled equilibria in (2.34), a family of kinetic models parametrized by the reference pressure reads
The kinetic equation in (2.35) shall be considered as a semi-phenomenological model of a non-ideal fluid, with the relaxation time ![]() $\tau$, the capillarity coefficient
$\tau$, the capillarity coefficient ![]() $\kappa$, pressure
$\kappa$, pressure ![]() $P$ and reference pressure
$P$ and reference pressure ![]() $P_0$ as phenomenological input parameters, while the Enskog–Vlasov realization will serve as a representative example for estimates of various flow regimes.
$P_0$ as phenomenological input parameters, while the Enskog–Vlasov realization will serve as a representative example for estimates of various flow regimes.
The analysis of the kinetic model in (2.35) under the conventional scaling of a small deviation from a uniform state (Chapman & Cowling Reference Chapman and Cowling1939),
is detailed in Appendix C. To second order in space derivatives, the resulting momentum balance equation reads
where the dynamic viscosity ![]() $\mu$ and the bulk viscosity
$\mu$ and the bulk viscosity ![]() $\eta$ in the Navier–Stokes stress tensor in (2.10) are defined by the reference pressure (
$\eta$ in the Navier–Stokes stress tensor in (2.10) are defined by the reference pressure (![]() $D=3$),
$D=3$),
Thus, the momentum balance equation in (2.37) is form-invariant with respect to the choice of reference pressure, provided ![]() $P_0$ satisfies a sub-isentropic condition,
$P_0$ satisfies a sub-isentropic condition,
for some ![]() $C>0$. With (2.40), the bulk viscosity in (2.39) is positive and vanishes when the reference pressure follows an isentropic process for ideal monatomic gas,
$C>0$. With (2.40), the bulk viscosity in (2.39) is positive and vanishes when the reference pressure follows an isentropic process for ideal monatomic gas, ![]() $P_0=C\rho ^{5/3}$. For example, any polytropic process,
$P_0=C\rho ^{5/3}$. For example, any polytropic process, ![]() $P_0=A\rho ^n$,
$P_0=A\rho ^n$, ![]() $1\le n\le 5/3$ satisfies the sub-isentropic condition and results in
$1\le n\le 5/3$ satisfies the sub-isentropic condition and results in ![]() $\eta =(5/3-n)\tau P_0$. A special case of the isothermal process
$\eta =(5/3-n)\tau P_0$. A special case of the isothermal process ![]() $n=1$ returns
$n=1$ returns ![]() $\eta =(2/3)\tau P_0$, and the viscous stress tensor becomes
$\eta =(2/3)\tau P_0$, and the viscous stress tensor becomes
However, when compared to the two-phase momentum equation in (2.12), the macroscopic limit recovers only the non-ideal gas component thereof while missing Korteweg's capillarity contribution. Indeed, the third-order term, ![]() $\sim \epsilon ^3\rho \boldsymbol {\nabla }\boldsymbol {\nabla }^2\rho$ in (2.28) and (2.35), does not contribute to the momentum equation in (2.37) under the scaling of (2.36a,b). This is consistent with the well-known results from kinetic theory (Chapman & Cowling Reference Chapman and Cowling1939) and is not surprising. The scaling of (2.36a,b) is essentially based on the Knudsen number, which overrides the relative contribution of the capillarity term by two orders, cf. Appendix C. Thus, under the weak non-uniformity assumption in (2.36a,b), the capillarity terms are seen as higher-order Burnett-level contributions, and cannot appear in the main (first and second) orders in the momentum balance equation of (2.37). In fact, the condition in (2.36a,b) rules out situations at an interface between phases where gradients of density become large over a relatively short distance. Therefore, for the kinetic model in (2.35) to recover in-full the momentum balance in (2.12), a different scaling needs to be applied.
$\sim \epsilon ^3\rho \boldsymbol {\nabla }\boldsymbol {\nabla }^2\rho$ in (2.28) and (2.35), does not contribute to the momentum equation in (2.37) under the scaling of (2.36a,b). This is consistent with the well-known results from kinetic theory (Chapman & Cowling Reference Chapman and Cowling1939) and is not surprising. The scaling of (2.36a,b) is essentially based on the Knudsen number, which overrides the relative contribution of the capillarity term by two orders, cf. Appendix C. Thus, under the weak non-uniformity assumption in (2.36a,b), the capillarity terms are seen as higher-order Burnett-level contributions, and cannot appear in the main (first and second) orders in the momentum balance equation of (2.37). In fact, the condition in (2.36a,b) rules out situations at an interface between phases where gradients of density become large over a relatively short distance. Therefore, for the kinetic model in (2.35) to recover in-full the momentum balance in (2.12), a different scaling needs to be applied.
2.3. Scaling by velocity increment and lattice Boltzmann equation
2.3.1. Time step and forcing
A rescaling of the kinetic model in this section shall be maintained by introducing a time step ![]() $\delta t$. As a preliminary consideration, we evaluate the contribution of the force term over the time step. To that end, as noted by Kupershtokh, Medvedev & Karpov (Reference Kupershtokh, Medvedev and Karpov2009), for a generic force
$\delta t$. As a preliminary consideration, we evaluate the contribution of the force term over the time step. To that end, as noted by Kupershtokh, Medvedev & Karpov (Reference Kupershtokh, Medvedev and Karpov2009), for a generic force ![]() $\boldsymbol {F}$, we can write the action of the force on the distribution function as a full derivative in a frame that moves with the local fluid velocity,
$\boldsymbol {F}$, we can write the action of the force on the distribution function as a full derivative in a frame that moves with the local fluid velocity,
Introducing the velocity increment,
and integrating in time, leads to an approximation,
This so-called exact difference method (EDM) becomes accurate for a gravity force, ![]() $\boldsymbol {F}/\rho ={\rm const.}$, otherwise it often provides a reliable estimate for the force term and is widely used. In what follows, the scaling to be applied assumes smallness of the velocity increment in (2.43) rather than smoothness of the spatial distribution of the force. Since the velocity increment is based on a time step, it is natural to proceed with a lattice Boltzmann realization of the kinetic equation.
$\boldsymbol {F}/\rho ={\rm const.}$, otherwise it often provides a reliable estimate for the force term and is widely used. In what follows, the scaling to be applied assumes smallness of the velocity increment in (2.43) rather than smoothness of the spatial distribution of the force. Since the velocity increment is based on a time step, it is natural to proceed with a lattice Boltzmann realization of the kinetic equation.
2.3.2. Standard lattice and product form
The lattice Boltzmann model shall be realized with the standard discrete velocity set ![]() $D3Q27$, where
$D3Q27$, where ![]() $D=3$ stands for three dimensions and
$D=3$ stands for three dimensions and ![]() $Q=27$ is the number of discrete velocities,
$Q=27$ is the number of discrete velocities,
We first define a triplet of functions in two variables, ![]() $\xi _{\alpha }$ and
$\xi _{\alpha }$ and ![]() $\zeta _{\alpha \alpha }$,
$\zeta _{\alpha \alpha }$,
and consider a product form associated with the discrete velocities ![]() $\boldsymbol {c}_i$ in (2.45a,b),
$\boldsymbol {c}_i$ in (2.45a,b),
All pertinent populations below shall be determined by specifying the parameters ![]() $\xi _\alpha$ and
$\xi _\alpha$ and ![]() $\zeta _{\alpha \alpha }$ in the product form in (2.49). A two-dimensional version of the model on the
$\zeta _{\alpha \alpha }$ in the product form in (2.49). A two-dimensional version of the model on the ![]() $D2Q9$ lattice is obtained by omitting the
$D2Q9$ lattice is obtained by omitting the ![]() $z$-component in all formulae below. Finally, we use the notation
$z$-component in all formulae below. Finally, we use the notation ![]() $\delta \boldsymbol {r}_{i}=\boldsymbol {c}_i\delta t$ for the lattice links, and denote the grid spacing in any direction
$\delta \boldsymbol {r}_{i}=\boldsymbol {c}_i\delta t$ for the lattice links, and denote the grid spacing in any direction ![]() $\alpha =x,y,z$ as
$\alpha =x,y,z$ as ![]() $\delta r=\vert c_{i\alpha }\vert \delta t$,
$\delta r=\vert c_{i\alpha }\vert \delta t$, ![]() $c_{i\alpha }\ne 0$. For the
$c_{i\alpha }\ne 0$. For the ![]() $D3Q27$ discrete velocity set in (2.45a,b), the lattice spacing is the same in all Cartesian directions.
$D3Q27$ discrete velocity set in (2.45a,b), the lattice spacing is the same in all Cartesian directions.
2.3.3. The lattice Boltzmann equation
The local density ![]() $\rho$ and flow velocity
$\rho$ and flow velocity ![]() $\boldsymbol {u}$ are defined using the populations
$\boldsymbol {u}$ are defined using the populations ![]() $f_i$,
$f_i$,
 $$\begin{gather} \rho(\boldsymbol{r},t)=\sum_{i=0}^{Q-1}f_i(\boldsymbol{r},t), \end{gather}$$
$$\begin{gather} \rho(\boldsymbol{r},t)=\sum_{i=0}^{Q-1}f_i(\boldsymbol{r},t), \end{gather}$$ $$\begin{gather}\rho\boldsymbol{u}(\boldsymbol{r},t)=\sum_{i=0}^{Q-1}\boldsymbol{c}_i\, f_i(\boldsymbol{r},t). \end{gather}$$
$$\begin{gather}\rho\boldsymbol{u}(\boldsymbol{r},t)=\sum_{i=0}^{Q-1}\boldsymbol{c}_i\, f_i(\boldsymbol{r},t). \end{gather}$$
With a reference pressure ![]() $P_0$, and by setting the parameters,
$P_0$, and by setting the parameters,
the local equilibrium populations are represented with the product-form in (2.49),
 \begin{equation} f_i^{eq}= \rho\prod_{\alpha=x,y,z}\varPsi_{c_{i\alpha}}\left(u_\alpha,\frac{P_0}{\rho}+u_{\alpha}^2\right). \end{equation}
\begin{equation} f_i^{eq}= \rho\prod_{\alpha=x,y,z}\varPsi_{c_{i\alpha}}\left(u_\alpha,\frac{P_0}{\rho}+u_{\alpha}^2\right). \end{equation}The LBGK equation, supplemented with a forcing term, is written as
where ![]() $\omega$ is a dimensionless relaxation parameter, the equilibrium populations are provided by (2.54), while the extended equilibrium populations
$\omega$ is a dimensionless relaxation parameter, the equilibrium populations are provided by (2.54), while the extended equilibrium populations ![]() $f_i^*$ are defined by the product-form in (2.49) with the following assignment for the parameters:
$f_i^*$ are defined by the product-form in (2.49) with the following assignment for the parameters:
where ![]() $\varPhi _{\alpha \alpha }/\rho$ is a correction term for the diagonals of the non-equilibrium momentum flux tensor,
$\varPhi _{\alpha \alpha }/\rho$ is a correction term for the diagonals of the non-equilibrium momentum flux tensor,
where ![]() $\varsigma = \delta r/\sqrt {3}\delta t$ is the so-called lattice speed of sound. The form of the correction term is a result of the multi-scale analysis presented in Appendix D. Thus, the extended equilibrium is explicitly written as
$\varsigma = \delta r/\sqrt {3}\delta t$ is the so-called lattice speed of sound. The form of the correction term is a result of the multi-scale analysis presented in Appendix D. Thus, the extended equilibrium is explicitly written as
 \begin{equation} f_i^*=\rho\prod_{\alpha=x,y,z}\varPsi_{c_{i\alpha}}\left(u_\alpha+\frac{F_{\alpha}\delta t}{\rho},\frac{P_0}{\rho}+u_{\alpha}^2+\frac{\varPhi_{\alpha\alpha}}{\rho}\right). \end{equation}
\begin{equation} f_i^*=\rho\prod_{\alpha=x,y,z}\varPsi_{c_{i\alpha}}\left(u_\alpha+\frac{F_{\alpha}\delta t}{\rho},\frac{P_0}{\rho}+u_{\alpha}^2+\frac{\varPhi_{\alpha\alpha}}{\rho}\right). \end{equation}Comments are in order.
• If the correction term of (2.58) is omitted in (2.57), the population in (2.59) becomes the equilibrium with the increment
 $\delta \boldsymbol {u}$ in (2.43) due to force action added to the flow velocity
$\delta \boldsymbol {u}$ in (2.43) due to force action added to the flow velocity  $\boldsymbol {u}$. This corresponds to the EDM forcing maintained by the second bracket in the right-hand side of the LBGK equation in (2.55).
$\boldsymbol {u}$. This corresponds to the EDM forcing maintained by the second bracket in the right-hand side of the LBGK equation in (2.55).• The correction term in (2.56) is added following a proposal by Saadat et al. (Reference Saadat, Hosseini, Dorschner and Karlin2021). Its purpose is to compensate for the bias of the
 $D3Q27$ velocities in (2.45a,b),
$D3Q27$ velocities in (2.45a,b),  $c_{i\alpha }^3=c_{i\alpha }$, and to restore the Galilean invariance of the normal components of the viscous stress tensor.
$c_{i\alpha }^3=c_{i\alpha }$, and to restore the Galilean invariance of the normal components of the viscous stress tensor.
The LBGK model in (2.55) is generic with respect to the choice of reference pressure ![]() $P_0$ and the force
$P_0$ and the force ![]() $\boldsymbol {F}$. We now proceed with the special case of Korteweg's force to establish a representation thereof matched to the lattice Boltzmann system.
$\boldsymbol {F}$. We now proceed with the special case of Korteweg's force to establish a representation thereof matched to the lattice Boltzmann system.
2.3.4. Pseudo-potential and capillarity
Following the representation in (2.14), Korteweg's force includes two distinct parts, the term supplying the non-ideal gas equation of state and the capillarity term responsible for the surface tension. Introducing a pseudo-potential ![]() $\psi$,
$\psi$,
 \begin{equation} \psi=\begin{cases} \sqrt{ P-P_0} & \text{if } P>P_0,\\ \sqrt{P_0-P} & \text{if } P \leq P_0, \end{cases} \end{equation}
\begin{equation} \psi=\begin{cases} \sqrt{ P-P_0} & \text{if } P>P_0,\\ \sqrt{P_0-P} & \text{if } P \leq P_0, \end{cases} \end{equation}Korteweg's force is written as
 \begin{equation} \boldsymbol{F} =\begin{cases} 2\psi\boldsymbol{\nabla}\psi - \kappa\rho\boldsymbol{\nabla}\boldsymbol{\nabla}^2\rho & \text{if } P>P_0,\\ -2\psi\boldsymbol{\nabla}\psi - \kappa\rho\boldsymbol{\nabla}\boldsymbol{\nabla}^2\rho & \text{if } P \leq P_0. \end{cases} \end{equation}
\begin{equation} \boldsymbol{F} =\begin{cases} 2\psi\boldsymbol{\nabla}\psi - \kappa\rho\boldsymbol{\nabla}\boldsymbol{\nabla}^2\rho & \text{if } P>P_0,\\ -2\psi\boldsymbol{\nabla}\psi - \kappa\rho\boldsymbol{\nabla}\boldsymbol{\nabla}^2\rho & \text{if } P \leq P_0. \end{cases} \end{equation}In the lattice Boltzmann setting, the pseudo-potential part is represented as a linear combination of the first- and second-neighbours contributions,
 \begin{equation} \delta t \psi(\boldsymbol{r})\boldsymbol{\nabla}\psi(\boldsymbol{r})= \psi(\boldsymbol{r})\sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_i [\mathcal{G}_1\psi(\boldsymbol{r}+\boldsymbol{c}_i \delta t) + \mathcal{G}_2\psi(\boldsymbol{r}+2\boldsymbol{c}_i \delta t)] + {O}([\delta r\boldsymbol{\nabla}]^5), \end{equation}
\begin{equation} \delta t \psi(\boldsymbol{r})\boldsymbol{\nabla}\psi(\boldsymbol{r})= \psi(\boldsymbol{r})\sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_i [\mathcal{G}_1\psi(\boldsymbol{r}+\boldsymbol{c}_i \delta t) + \mathcal{G}_2\psi(\boldsymbol{r}+2\boldsymbol{c}_i \delta t)] + {O}([\delta r\boldsymbol{\nabla}]^5), \end{equation}
where the weights ![]() $w_i$ are defined by the product-form in (2.49) at
$w_i$ are defined by the product-form in (2.49) at ![]() $\xi _{\alpha }=0$,
$\xi _{\alpha }=0$, ![]() $\zeta _{\alpha \alpha }=\varsigma ^2$,
$\zeta _{\alpha \alpha }=\varsigma ^2$,
and where the parameters ![]() $\mathcal {G}_1$ and
$\mathcal {G}_1$ and ![]() $\mathcal {G}_2$ satisfy the conditions,
$\mathcal {G}_2$ satisfy the conditions,
The condition in (2.64) maintains the equation of state, while the condition in (2.65) eliminates the third-order error. Non-compliance with the first and/or second condition would introduce respectively deviations of order ![]() ${O}([\delta r\boldsymbol {\nabla }])$ and/or
${O}([\delta r\boldsymbol {\nabla }])$ and/or ![]() ${O}([\delta r\boldsymbol {\nabla }]^3)$ from the target Korteweg stress tensor.
${O}([\delta r\boldsymbol {\nabla }]^3)$ from the target Korteweg stress tensor.
The capillarity part of Korteweg's force in (2.61) is represented in a similar way but using the density instead of the pseudo-potential,
 \begin{align} \delta t \tilde{\kappa}\rho(\boldsymbol{r})\boldsymbol{\nabla}\boldsymbol{\nabla}^2\rho(\boldsymbol{r}) &= \rho(\boldsymbol{r})\sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_i [\mathcal{G}_3\rho(\boldsymbol{r}+\boldsymbol{c}_i \delta t) + \mathcal{G}_4 \rho(\boldsymbol{r}+2\boldsymbol{c}_i \delta t)]\nonumber\\ &\quad + {O}([\delta r\boldsymbol{\nabla}]^5), \end{align}
\begin{align} \delta t \tilde{\kappa}\rho(\boldsymbol{r})\boldsymbol{\nabla}\boldsymbol{\nabla}^2\rho(\boldsymbol{r}) &= \rho(\boldsymbol{r})\sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_i [\mathcal{G}_3\rho(\boldsymbol{r}+\boldsymbol{c}_i \delta t) + \mathcal{G}_4 \rho(\boldsymbol{r}+2\boldsymbol{c}_i \delta t)]\nonumber\\ &\quad + {O}([\delta r\boldsymbol{\nabla}]^5), \end{align}
where ![]() $\tilde {\kappa }=\kappa \delta r^2$ and the parameters
$\tilde {\kappa }=\kappa \delta r^2$ and the parameters ![]() $\mathcal {G}_3$ and
$\mathcal {G}_3$ and ![]() $\mathcal {G}_4$ satisfy the conditions,
$\mathcal {G}_4$ satisfy the conditions,
The condition in (2.67) cancels the first-order derivative, while the condition in (2.68) maintains the capillarity contribution. Combining both contributions of the pseudo-potential in (2.62) and the capillarity in (2.66), we obtain the lattice Boltzmann form of Korteweg's force in (2.61) as
 \begin{align} \delta t\boldsymbol{F} &={\pm} 2\psi(\boldsymbol{r})\sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_i \left[\frac{4}{3}\psi(\boldsymbol{r}+\boldsymbol{c}_i\delta t) - \frac{1}{6} \psi(\boldsymbol{r}+2\boldsymbol{c}_i\delta t)\right]\nonumber\\ &\quad +\tilde{\kappa}\rho(\boldsymbol{r})\sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_i [2\rho(\boldsymbol{r}+\boldsymbol{c}_i\delta t) - \rho(\boldsymbol{r}+2\boldsymbol{c}_i\delta t)] + {O}([\delta r\boldsymbol{\nabla}]^5), \end{align}
\begin{align} \delta t\boldsymbol{F} &={\pm} 2\psi(\boldsymbol{r})\sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_i \left[\frac{4}{3}\psi(\boldsymbol{r}+\boldsymbol{c}_i\delta t) - \frac{1}{6} \psi(\boldsymbol{r}+2\boldsymbol{c}_i\delta t)\right]\nonumber\\ &\quad +\tilde{\kappa}\rho(\boldsymbol{r})\sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_i [2\rho(\boldsymbol{r}+\boldsymbol{c}_i\delta t) - \rho(\boldsymbol{r}+2\boldsymbol{c}_i\delta t)] + {O}([\delta r\boldsymbol{\nabla}]^5), \end{align}where the sign convention follows (2.61).
In the context of the lattice Boltzmann method, various pseudo-potential representations have long been in use, and comments are to make a distinction to the present formulation.
• By setting
 $\mathcal {G}_2=0$ in (2.62) and ignoring Korteweg's capillarity term in (2.66) by choosing
$\mathcal {G}_2=0$ in (2.62) and ignoring Korteweg's capillarity term in (2.66) by choosing  $\mathcal {G}_3=\mathcal {G}_4=0$, one recovers a model first proposed by Shan & Chen (Reference Shan and Chen1993) for special equations of state (see (G1), (G2), (G3) in Appendix G) and extended to a general equation of state by Yuan & Schaefer (Reference Yuan and Schaefer2006). Unlike the above condition in (2.65) which eliminates the third-order error in the pseudo-potential part of Korteweg's force in (2.14), the model of Shan & Chen (Reference Shan and Chen1993) requires the third-order Korteweg-like term to be retained so that it mimics surface tension effects. Consequently, the force in the models of Shan & Chen (Reference Shan and Chen1993), Yuan & Schaefer (Reference Yuan and Schaefer2006) becomes
(2.70)The force in (2.70) neither conforms with the van der Waals second-gradient theory and Korteweg's stress of § 2.1 (unless
$\mathcal {G}_3=\mathcal {G}_4=0$, one recovers a model first proposed by Shan & Chen (Reference Shan and Chen1993) for special equations of state (see (G1), (G2), (G3) in Appendix G) and extended to a general equation of state by Yuan & Schaefer (Reference Yuan and Schaefer2006). Unlike the above condition in (2.65) which eliminates the third-order error in the pseudo-potential part of Korteweg's force in (2.14), the model of Shan & Chen (Reference Shan and Chen1993) requires the third-order Korteweg-like term to be retained so that it mimics surface tension effects. Consequently, the force in the models of Shan & Chen (Reference Shan and Chen1993), Yuan & Schaefer (Reference Yuan and Schaefer2006) becomes
(2.70)The force in (2.70) neither conforms with the van der Waals second-gradient theory and Korteweg's stress of § 2.1 (unless \begin{equation} \boldsymbol{F}_{SC}=2\psi\boldsymbol{\nabla}\psi+\tfrac{1}{3}\psi\boldsymbol{\nabla}\boldsymbol{\nabla}^2\psi. \end{equation}
\begin{equation} \boldsymbol{F}_{SC}=2\psi\boldsymbol{\nabla}\psi+\tfrac{1}{3}\psi\boldsymbol{\nabla}\boldsymbol{\nabla}^2\psi. \end{equation} $\psi =A\rho$ which, however, does not lead to phase separation), nor can it be derived from the BBGKY equation with a central-force particles interaction of § 2.2. Another relatively minor issue is the fixed parameter
$\psi =A\rho$ which, however, does not lead to phase separation), nor can it be derived from the BBGKY equation with a central-force particles interaction of § 2.2. Another relatively minor issue is the fixed parameter  $1/3$, which is mimicking the capillarity coefficient and is the result of the third-order error retained in the expansion.
$1/3$, which is mimicking the capillarity coefficient and is the result of the third-order error retained in the expansion.• By imposing the condition in (2.64) while still discarding Korteweg's capillarity contribution in (2.66), one arrives at a dual-range force model of Sbragaglia et al. (Reference Sbragaglia, Benzi, Biferale, Succi, Sugiyama and Toschi2007), Shan (Reference Shan2008),
(2.71)The model in (2.71) is an improvement on the first-neighbour model in (2.70), in that it allows for a variable capillarity-like coefficient. At the same time, it does not resolve the inconsistency with Korteweg's stress tensor. \begin{equation} \boldsymbol{F}_{DR}=2\psi\boldsymbol{\nabla}\psi+(\tfrac{4}{3}-\mathcal{G}_1) \psi\boldsymbol{\nabla}\boldsymbol{\nabla}^2\psi. \end{equation}
\begin{equation} \boldsymbol{F}_{DR}=2\psi\boldsymbol{\nabla}\psi+(\tfrac{4}{3}-\mathcal{G}_1) \psi\boldsymbol{\nabla}\boldsymbol{\nabla}^2\psi. \end{equation}• Various other modifications of the original models of Shan & Chen (Reference Shan and Chen1993) were proposed to improve on the main inconsistency by introducing and tuning ad hoc numerical coefficients tailored to a selected equation of state (Kupershtokh et al. Reference Kupershtokh, Medvedev and Karpov2009; Li, Luo & Li Reference Li, Luo and Li2013; Huang, Yin & Killough Reference Huang, Yin and Killough2019; Luo, Fei & Wang Reference Luo, Fei and Wang2021). However, to the best of our knowledge, none of these proposals came to recognize that the problem lies in the fact that it is impossible to represent both parts of Korteweg's force, the non-ideal equation of state and the capillarity term, while using a pseudo-potential alone. This fact follows both from the phenomenological thermodynamics reviewed in § 2.1, as well as from a more microscopic approach of § 2.2. The pseudo-potential in both cases represents only the equation of state, while the capillarity term requires the density field to be used, as featured by (2.66).
• Pseudo-potential is a convenient form of representing the equation of state contribution to Korteweg's force, tailored to the lattice Boltzmann setting. If other numerical methods are used to evaluate the force in (2.61), such as higher-order finite difference, the model is usually renamed to a free energy approach.
With the generic LBGK model in (2.55) and Korteweg's force in (2.69) both specified, we proceed to the analysis of the hydrodynamic limit under a suitable scaling.
2.3.5. Hydrodynamic limit under small velocity increment scaling
Chapman–Enskog analysis of the LBGK equation in (2.55) was performed under the following scaling. With the characteristic values of the flow velocity ![]() $\mathcal {U}$, the flow scale
$\mathcal {U}$, the flow scale ![]() $\mathcal {L}$, the density
$\mathcal {L}$, the density ![]() $\rho$, the force
$\rho$, the force ![]() $\mathcal {F}$ and the velocity increment
$\mathcal {F}$ and the velocity increment ![]() $\delta u$, the following conditions apply:
$\delta u$, the following conditions apply:
The first scaling condition in (2.72) refers to a smallness of velocity increment, that is, to the smallness of the force action over time ![]() $\delta t$. The second scaling condition in (2.73) is a resolution requirement. Both conditions are assumed to hold simultaneously. Details of the analysis are provided in Appendix D while the result is summarized below.
$\delta t$. The second scaling condition in (2.73) is a resolution requirement. Both conditions are assumed to hold simultaneously. Details of the analysis are provided in Appendix D while the result is summarized below.
Let us introduce a transformed velocity ![]() $\boldsymbol {U}$ by shifting the local velocity
$\boldsymbol {U}$ by shifting the local velocity ![]() $\boldsymbol {u}$ by half of the velocity increment
$\boldsymbol {u}$ by half of the velocity increment ![]() $\delta \boldsymbol {u}$ in (2.43),
$\delta \boldsymbol {u}$ in (2.43),
Then the following mass and momentum balance equations to second order in ![]() $\varepsilon$ are recovered when the force in (2.69) is used under the scaling in (2.72) and (2.73),
$\varepsilon$ are recovered when the force in (2.69) is used under the scaling in (2.72) and (2.73),
where the dynamic and the bulk viscosity in the Navier–Stokes stress tensor in (2.10) are related to the relaxation parameter ![]() $\omega$ and the reference pressure
$\omega$ and the reference pressure ![]() $P_0$ as follows:
$P_0$ as follows:
Unlike the previous result in (2.37), the momentum balance in (2.76) includes not only the non-ideal gas pressure but also the capillarity term, and is thus consistent with Korteweg's force in the momentum balance. It should be pointed out that the scaling in (2.72) refers to the smallness of the increment of the flow velocity rather than to the smallness of either the time step or of the force. Thus, rescaling the kinetic model in (2.35) based on the smallness of the flow velocity increments results in both the non-ideal gas equation of state and the capillarity revealed at the Euler level ![]() $O(\varepsilon )$ of the momentum balance in (2.76). This is in contrast to the conventional scaling, which is tied to the non-uniformity and surface tension that would appear only at a Burnett level
$O(\varepsilon )$ of the momentum balance in (2.76). This is in contrast to the conventional scaling, which is tied to the non-uniformity and surface tension that would appear only at a Burnett level ![]() $O(\epsilon ^3)$.
$O(\epsilon ^3)$.
2.3.6. Code structure
The structure of the algorithm is given in figure 1. The algorithm consists of four main building blocks: (a) evaluation of macroscopic variables ![]() $\rho$,
$\rho$, ![]() $\boldsymbol {u}$ and
$\boldsymbol {u}$ and ![]() $P_0$ via (2.50); (b) evaluation of non-local macroscopic contributions
$P_0$ via (2.50); (b) evaluation of non-local macroscopic contributions ![]() $\varPhi _{\alpha \alpha }$ and
$\varPhi _{\alpha \alpha }$ and ![]() $F_{\alpha }$ via (2.58), (2.69) and (2.60); (c) evaluation of equilibrium and extended equilibrium functions via (2.54) and (2.59) and (d) discrete space/time evolution following (2.55).
$F_{\alpha }$ via (2.58), (2.69) and (2.60); (c) evaluation of equilibrium and extended equilibrium functions via (2.54) and (2.59) and (d) discrete space/time evolution following (2.55).

Figure 1. Flow chart for a typical code based on the proposed two-phase lattice Boltzmann model.
In the remainder of this paper, and without loss of generality, we set the reference pressure ![]() $P_0=\varsigma ^2\rho$ to minimize the correction term in (2.58). This choice of reference pressure follows the third-order quadrature leading to the family of lattices used here and is quite common in both ideal and non-ideal fluid lattice Boltzmann simulations (Krüger et al. Reference Krüger, Kusumaatmaja, Kuzmin, Shardt, Silva and Viggen2017). Other possibilities of choosing the reference pressure are illustrated in Appendix H. In the next section, the model is scrutinized by a set of numerical tests probing various aspects of thermo- and hydrodynamic consistency.
$P_0=\varsigma ^2\rho$ to minimize the correction term in (2.58). This choice of reference pressure follows the third-order quadrature leading to the family of lattices used here and is quite common in both ideal and non-ideal fluid lattice Boltzmann simulations (Krüger et al. Reference Krüger, Kusumaatmaja, Kuzmin, Shardt, Silva and Viggen2017). Other possibilities of choosing the reference pressure are illustrated in Appendix H. In the next section, the model is scrutinized by a set of numerical tests probing various aspects of thermo- and hydrodynamic consistency.
3. Thermodynamic consistency
3.1. Liquid–vapour coexistence
We begin with the validation of liquid–vapour coexistence. Two-dimensional flat interface simulations were performed on a grid ![]() $800\times 10$, filled with the vapour phase of a fluid with a specified equation of state and periodic boundary conditions. A column of the liquid phase over 400 grid-points was placed at the centre of the domain. Simulations were ran until the steady state was reached. The steady state was monitored via an
$800\times 10$, filled with the vapour phase of a fluid with a specified equation of state and periodic boundary conditions. A column of the liquid phase over 400 grid-points was placed at the centre of the domain. Simulations were ran until the steady state was reached. The steady state was monitored via an ![]() $L_0$ norm convergence criterion based on the liquid density
$L_0$ norm convergence criterion based on the liquid density ![]() $\rho _l$ at the centre of the drop and the vapour density
$\rho _l$ at the centre of the drop and the vapour density ![]() $\rho _v$ at a location outside the drop. A theoretical prediction for the coexistence density ratio
$\rho _v$ at a location outside the drop. A theoretical prediction for the coexistence density ratio ![]() $\rho _l/\rho _v$ is readily obtained via the equilibrium condition leading to the Maxwell equal-area construction,
$\rho _l/\rho _v$ is readily obtained via the equilibrium condition leading to the Maxwell equal-area construction,
where ![]() $P_{sat}(T)$ is the saturation pressure at which the liquid and vapour phases coexist at a given temperature
$P_{sat}(T)$ is the saturation pressure at which the liquid and vapour phases coexist at a given temperature ![]() $T$ below the critical point.
$T$ below the critical point.
Initially, four generally adopted equations of state (EoS) were considered: the van der Waals EoS (van der Waals Reference van der Waals1873),
where parameters ![]() $a$ and
$a$ and ![]() $b$ are related to critical temperature
$b$ are related to critical temperature ![]() $T_c$ and pressure
$T_c$ and pressure ![]() $P_c$ as
$P_c$ as
the Peng–Robinson EoS (Peng & Robinson Reference Peng and Robinson1976),
with
where ![]() $\omega '$ the acentric factor (
$\omega '$ the acentric factor (![]() $\omega '=0.344$ for water), and
$\omega '=0.344$ for water), and
the Riedlich–Kwong–Soave EoS (Redlich & Kwong Reference Redlich and Kwong1949; Soave Reference Soave1972),
with
and
and the Carnahan–Starling EoS (Carnahan & Starling Reference Carnahan and Starling1969),
 \begin{equation} P = \rho R T \frac{1+b\rho/4 + {(b\rho/4)}^2 - {(b\rho/4)}^3}{{(1-b\rho/4)}^3} - a\rho^2, \end{equation}
\begin{equation} P = \rho R T \frac{1+b\rho/4 + {(b\rho/4)}^2 - {(b\rho/4)}^3}{{(1-b\rho/4)}^3} - a\rho^2, \end{equation}with
Figure 2 demonstrates that the stationary density ratios ![]() $\rho _l/\rho _v$ obtained from the simulation are in excellent agreement with the theoretical coexisting liquid–vapour density ratios that are defined by Maxwell's equal-area rule in (3.1), for all four equations of state and for ratios as high as at least
$\rho _l/\rho _v$ obtained from the simulation are in excellent agreement with the theoretical coexisting liquid–vapour density ratios that are defined by Maxwell's equal-area rule in (3.1), for all four equations of state and for ratios as high as at least ![]() $\rho _l/\rho _v\sim 10^{11}$. It is noted that high coexisting density ratios were obtained without any tuning parameters, universally for all equations of state considered. Therefore, and without loss of generality, in the remainder of this article, we only consider the van der Waals equation of state in (3.2).
$\rho _l/\rho _v\sim 10^{11}$. It is noted that high coexisting density ratios were obtained without any tuning parameters, universally for all equations of state considered. Therefore, and without loss of generality, in the remainder of this article, we only consider the van der Waals equation of state in (3.2).

Figure 2. Liquid–vapour coexistence for various equations of state. Grey lines, Maxwell's equal-area construction in (3.1). Red symbol, simulation. (a) van der Waals (3.2) (![]() $a=0.000159$,
$a=0.000159$, ![]() $b=0.0952$); (b) Peng–Robinson (3.4) (
$b=0.0952$); (b) Peng–Robinson (3.4) (![]() $a=0.000159$,
$a=0.000159$, ![]() $b=0.0952$); (c) Carnahan–Starling (3.10) (
$b=0.0952$); (c) Carnahan–Starling (3.10) (![]() $a=0.000868$,
$a=0.000868$, ![]() $b=4$); (d) Riedlich–Kwong–Soave (3.7) (
$b=4$); (d) Riedlich–Kwong–Soave (3.7) (![]() $a=0.000159$,
$a=0.000159$, ![]() $b=0.0952$). For all simulations,
$b=0.0952$). For all simulations, ![]() $\tilde {\kappa }=0.02$.
$\tilde {\kappa }=0.02$.
3.2. The principle of corresponding states and thermodynamic convergence
A discussion on the principle of corresponding states and the necessity of adherence to it in the context of the van der Waals theory of a capillary fluid in the simulation of realistic systems at large density ratios is in order. According to Guggenheim (Reference Guggenheim1945), the principle of corresponding states is ‘the most useful byproduct of van der Waals’ equation of state’. The principle maintains that all properties that depend on inter-molecular forces are related to the critical properties of the substance in a universal way, regardless of the molecular compound of interest. While for real fluids, as shown by Guggenheim (Reference Guggenheim1945), the principle is an approximation, it is an exact property within the van der Waals capillary fluids theory. This is, most notably, shown by the absence of substance-dependent parameters in the non-dimensional form of the van der Waals equation of state and mean-field scaling laws. For the equation of state, the principle of corresponding states implies that the reduced pressure ![]() $P_r=P/P_c$ is a universal function of the reduced temperature
$P_r=P/P_c$ is a universal function of the reduced temperature ![]() $T_r=T/T_c$ and of the reduced density
$T_r=T/T_c$ and of the reduced density ![]() $\rho _r=\rho /\rho _c$,
$\rho _r=\rho /\rho _c$,
The universality of the reduced pressure in (3.12) can be used to write Maxwell's equal-area rule in reduced form,
The coexistence density ratio ![]() $\rho _l/\rho _v$ at a given reduced temperature
$\rho _l/\rho _v$ at a given reduced temperature ![]() $T_r$ is therefore also universal. Deviation from these universal values can be rooted either in numerical artefacts or inconsistent thermodynamics of the model. For a consistent discretization in the sense of Lax's equivalence theorem (Lax & Richtmyer Reference Lax and Richtmyer1956), the former should be vanishing in the limit of a well-resolved simulation. The substance-agnostic form of the non-dimensional equations, i.e. the principle of corresponding states, allows us to probe convergence by systematically thickening the interface.
$T_r$ is therefore also universal. Deviation from these universal values can be rooted either in numerical artefacts or inconsistent thermodynamics of the model. For a consistent discretization in the sense of Lax's equivalence theorem (Lax & Richtmyer Reference Lax and Richtmyer1956), the former should be vanishing in the limit of a well-resolved simulation. The substance-agnostic form of the non-dimensional equations, i.e. the principle of corresponding states, allows us to probe convergence by systematically thickening the interface.
To probe the consistency with the principle of corresponding states in our model, we performed simulations for different values of the weak attraction parameter ![]() $a$ of the van der Waals equation of state in (3.2). Reduced coexistence densities are shown in figure 3 for four different values of
$a$ of the van der Waals equation of state in (3.2). Reduced coexistence densities are shown in figure 3 for four different values of ![]() $a$. It is observed that, down from the critical point to
$a$. It is observed that, down from the critical point to ![]() $T_r\approx 0.4$, coexistence densities essentially overlap for all the four values of
$T_r\approx 0.4$, coexistence densities essentially overlap for all the four values of ![]() $a$, in agreement with the principle of corresponding states. Deviations from the principle of corresponding states are most pronounced on the vapour side, as observed in figure 3. This can be explained as follows. The local value of the scaling parameter
$a$, in agreement with the principle of corresponding states. Deviations from the principle of corresponding states are most pronounced on the vapour side, as observed in figure 3. This can be explained as follows. The local value of the scaling parameter ![]() $\varepsilon$ in (2.72) is estimated as
$\varepsilon$ in (2.72) is estimated as ![]() $\varepsilon _{l,v}\sim \delta t \mathcal {F}/\rho _{l,v}\mathcal {U}$ in the liquid and in the vapour, respectively. Hence, their relative magnitude scales as the inverse of the density ratio,
$\varepsilon _{l,v}\sim \delta t \mathcal {F}/\rho _{l,v}\mathcal {U}$ in the liquid and in the vapour, respectively. Hence, their relative magnitude scales as the inverse of the density ratio, ![]() $\varepsilon _{v}/\varepsilon _l\sim \rho _l/\rho _v$. Thus, even if the scaling condition in (2.72) is satisfied for the liquid,
$\varepsilon _{v}/\varepsilon _l\sim \rho _l/\rho _v$. Thus, even if the scaling condition in (2.72) is satisfied for the liquid, ![]() $\varepsilon _l\ll 1$, it is still prone to violation for the vapour, if the density ratio
$\varepsilon _l\ll 1$, it is still prone to violation for the vapour, if the density ratio ![]() $\rho _l/\rho _v$ becomes sufficiently large. Conversely, if the scaling condition is satisfied for vapour,
$\rho _l/\rho _v$ becomes sufficiently large. Conversely, if the scaling condition is satisfied for vapour, ![]() $\epsilon _v\ll 1$, it is also satisfied for liquid. Furthermore, due to the scaling relation between interface width and temperature detailed in § 3.6, the interface gets thinner at lower temperatures. This in turn means that for a given
$\epsilon _v\ll 1$, it is also satisfied for liquid. Furthermore, due to the scaling relation between interface width and temperature detailed in § 3.6, the interface gets thinner at lower temperatures. This in turn means that for a given ![]() $\delta r$, fewer grid-points resolve the interface with decreasing temperature. Whenever the parameters
$\delta r$, fewer grid-points resolve the interface with decreasing temperature. Whenever the parameters ![]() ${\delta r}/{W}$ and
${\delta r}/{W}$ and ![]() ${\delta t F}/{\rho \mathcal {U}}$ increase, contributions of higher orders in
${\delta t F}/{\rho \mathcal {U}}$ increase, contributions of higher orders in ![]() $\varepsilon$ become significant and lead to deviations from the analytical predictions. The characteristic interface width scales as
$\varepsilon$ become significant and lead to deviations from the analytical predictions. The characteristic interface width scales as ![]() $W \propto 1/\sqrt {a}$ (Jamet et al. Reference Jamet, Lebaigue, Coutris and Delhaye2001). As such, lower values of
$W \propto 1/\sqrt {a}$ (Jamet et al. Reference Jamet, Lebaigue, Coutris and Delhaye2001). As such, lower values of ![]() $a$ lead to larger
$a$ lead to larger ![]() $W$, in parallel with smaller force increments over
$W$, in parallel with smaller force increments over ![]() $\delta t$, which restores dominance of order
$\delta t$, which restores dominance of order ![]() $\varepsilon$ terms over Burnett and super-Burnett level contributions, and therefore the corresponding states principle. This last point is demonstrated by the convergence of the coexistence density ratio to the analytical predictions with decreasing
$\varepsilon$ terms over Burnett and super-Burnett level contributions, and therefore the corresponding states principle. This last point is demonstrated by the convergence of the coexistence density ratio to the analytical predictions with decreasing ![]() $a$. For well-resolved simulations, as shown in figure 2, the model correctly recovers the coexistence densities and thus complies with the principle of corresponding states. Below, we refer to the convergence of the scheme to the principle of corresponding states as the thermodynamic convergence.
$a$. For well-resolved simulations, as shown in figure 2, the model correctly recovers the coexistence densities and thus complies with the principle of corresponding states. Below, we refer to the convergence of the scheme to the principle of corresponding states as the thermodynamic convergence.

Figure 3. Convergence to the principle of corresponding states. Coexistence densities as obtained from (grey lines) Maxwell's construction and (markers) simulations with different choices of ![]() $a$: (green
$a$: (green ![]() $\times$)
$\times$) ![]() $a=0.0102$; (magenta
$a=0.0102$; (magenta ![]() $+$)
$+$) ![]() $a=0.0051$; (blue triangles)
$a=0.0051$; (blue triangles) ![]() $a=0.0026$; (red squares)
$a=0.0026$; (red squares) ![]() $a=0.0013$ and (black circles)
$a=0.0013$ and (black circles) ![]() $a=0.00064$.
$a=0.00064$.
To further clarify the utility of the principle of corresponding states in probing convergence, we have also conducted simulations similar to those reported in figure 3, with the first-neighbour pseudo-potential model (Shan & Chen Reference Shan and Chen1993), (2.70), supplemented with the van der Waals equation of state (Yuan & Schaefer Reference Yuan and Schaefer2006). The results are shown in figure 4. Two points are worth noting here. First, a notion of convergence is present as co-existence densities do converge to a limit. However, that limit does not correspond to the capillary fluid model. Deviations become pronounced at lower temperatures where density ratios are larger. These differences are explained by the thermodynamic consistency issue where the mechanical stability condition governing the classical pseudo-potential model is recovered as (Benzi et al. Reference Benzi, Biferale, Sbragaglia, Succi and Toschi2006; Shan Reference Shan2008)
which is different from (3.13). Here ![]() $\psi _r=\psi /\psi _c$, where
$\psi _r=\psi /\psi _c$, where ![]() $\psi _c$ is the pseudo-potential at critical state. This in turn naturally leads to observations of figure 4 where the discrete solver is convergent, but to a continuum-level behaviour dictated by (3.14) rather than the capillary fluid of (3.13). It is worth nothing that a number of numerical modifications have been proposed to improve on this issue. A detailed overview of such changes is out of the scope of the present work. Interested readers are referred to Chen et al. (Reference Chen, Kang, Mu, He and Tao2014) for a review.
$\psi _c$ is the pseudo-potential at critical state. This in turn naturally leads to observations of figure 4 where the discrete solver is convergent, but to a continuum-level behaviour dictated by (3.14) rather than the capillary fluid of (3.13). It is worth nothing that a number of numerical modifications have been proposed to improve on this issue. A detailed overview of such changes is out of the scope of the present work. Interested readers are referred to Chen et al. (Reference Chen, Kang, Mu, He and Tao2014) for a review.

Figure 4. Coexistence densities as obtained from (grey lines) Maxwell's construction and (markers) simulations with different choices of ![]() $a$: (green
$a$: (green ![]() $\times$)
$\times$) ![]() $a=0.0102$; (magenta
$a=0.0102$; (magenta ![]() $+$)
$+$) ![]() $a=0.0051$; (blue triangles)
$a=0.0051$; (blue triangles) ![]() $a=0.0026$; (red squares)
$a=0.0026$; (red squares) ![]() $a=0.0013$ and (black circles)
$a=0.0013$ and (black circles) ![]() $a=0.00064$. Simulations are conducted using the first-neighbour pseudo-potential model in (2.70).
$a=0.00064$. Simulations are conducted using the first-neighbour pseudo-potential model in (2.70).
3.3. Temperature dependence of the surface tension near the critical point
Surface tension at the liquid–vapour interface decreases with increasing temperature and vanishes at the critical point (Guggenheim Reference Guggenheim1945). For the van der Waals equation of state, the surface tension coefficient ![]() $\sigma$ follows a scaling law as
$\sigma$ follows a scaling law as ![]() $T_r\to 1$ (van der Waals Reference van der Waals1894; Blokhuis & Kuipers Reference Blokhuis and Kuipers2006),
$T_r\to 1$ (van der Waals Reference van der Waals1894; Blokhuis & Kuipers Reference Blokhuis and Kuipers2006),
To probe the consistency of the proposed lattice Boltzmann model, the temperature dependence of the surface tension was numerically measured in two different configurations, the flat interface and the circular drop, in a temperature interval ![]() $T_r\in [0.85,\, 1]$.
$T_r\in [0.85,\, 1]$.
In the first configuration, the surface tension coefficient was evaluated using its definition for the flat interface (Kirkwood & Buff Reference Kirkwood and Buff1949),
where the interface is normal to the ![]() $x$-axis in a two-dimensional simulation setup. The normal
$x$-axis in a two-dimensional simulation setup. The normal ![]() $P_{xx}$ and the tangential
$P_{xx}$ and the tangential ![]() $P_{yy}$ components of the discrete pressure tensor were computed using a formalism developed in Appendix E, following a proposal by Shan (Reference Shan2008).
$P_{yy}$ components of the discrete pressure tensor were computed using a formalism developed in Appendix E, following a proposal by Shan (Reference Shan2008).
In the second configuration, simulations of circular liquid drops surrounded with vapour at the centre of a square domain were conducted. At each temperature, four different initial drop radii were considered, ![]() $R_0\in \{45,55,65,75\}$, chosen in such a way that the interface width is sufficiently small compared to the initial drop radius. In the simulation, we used
$R_0\in \{45,55,65,75\}$, chosen in such a way that the interface width is sufficiently small compared to the initial drop radius. In the simulation, we used ![]() $W/R_0 \le 0.1$, where
$W/R_0 \le 0.1$, where ![]() $W=(\rho _l-\rho _v)/\max \lvert \boldsymbol {\nabla }\rho \lvert$ is the interface width, to minimize the curvature dependence of surface tension. The corresponding surface tension coefficient was evaluated using the Laplace law (
$W=(\rho _l-\rho _v)/\max \lvert \boldsymbol {\nabla }\rho \lvert$ is the interface width, to minimize the curvature dependence of surface tension. The corresponding surface tension coefficient was evaluated using the Laplace law (![]() $D=2$) in a form,
$D=2$) in a form,
where the radius ![]() $R_e$ corresponds to the equimolar dividing surface (Gibbs Reference Gibbs1874).
$R_e$ corresponds to the equimolar dividing surface (Gibbs Reference Gibbs1874).
A brief reminder of Gibbs’ theory of dividing surfaces is in order. The total mass in both the diffuse and sharp interface pictures can be written as
where ![]() $\rho _l V_l$ and
$\rho _l V_l$ and ![]() $\rho _v V_v$ are the masses in the bulk liquid and vapour phases in the sharp interface picture, while
$\rho _v V_v$ are the masses in the bulk liquid and vapour phases in the sharp interface picture, while ![]() $\varGamma$ is the excess mass on a dividing surface
$\varGamma$ is the excess mass on a dividing surface ![]() $\varSigma$, or mass adsorbance (Gibbs Reference Gibbs1874). By requiring that no mass be stored on the dividing surface, we get the definition of the equimolar surface,
$\varSigma$, or mass adsorbance (Gibbs Reference Gibbs1874). By requiring that no mass be stored on the dividing surface, we get the definition of the equimolar surface,
The family of dividing surfaces in the case of drop or bubble are concentric spheres (![]() $D=3$) or concentric circles (
$D=3$) or concentric circles (![]() $D=2$) parametrized by their radius
$D=2$) parametrized by their radius ![]() $R$. In particular, for a two-dimensional drop, the mass adsorbance can be written as a function of the radius of the dividing circle,
$R$. In particular, for a two-dimensional drop, the mass adsorbance can be written as a function of the radius of the dividing circle,
while the zero-adsorption condition in (3.19), ![]() $\varGamma (R_e)=0$, implies the equimolar radius
$\varGamma (R_e)=0$, implies the equimolar radius ![]() $R_e$,
$R_e$,
 \begin{equation} R_e = \sqrt{\frac{\displaystyle\int_0^{\infty}(\rho(r) - \rho_v)r \,{\rm d}r}{(\rho_l - \rho_v)}}. \end{equation}
\begin{equation} R_e = \sqrt{\frac{\displaystyle\int_0^{\infty}(\rho(r) - \rho_v)r \,{\rm d}r}{(\rho_l - \rho_v)}}. \end{equation}The drop configuration along with the scaling of the pressure difference across the interface with drop radius are shown in figure 5.

Figure 5. (a) Circular ![]() $D=2$ drop configurations; (b) pressure difference scaling with drop radius for
$D=2$ drop configurations; (b) pressure difference scaling with drop radius for ![]() $T_r=0.99$, 0.98, 0.97 and 0.96. The pressure difference is defined as
$T_r=0.99$, 0.98, 0.97 and 0.96. The pressure difference is defined as ![]() $\Delta P=P_{in}-P_{out}$. The slope of the straight line is the surface tension coefficient.
$\Delta P=P_{in}-P_{out}$. The slope of the straight line is the surface tension coefficient.
The results as obtained from both the flat interface and the drop configurations are shown in figure 6. It is clearly observed that the surface tensions as obtained from the proposed formulation (using either one of the considered configurations) agree very well with (3.15), provided that ![]() $W \ll R_{e}$. Discussion of the curvature dependence of surface tension shall be continued in § 3.5.
$W \ll R_{e}$. Discussion of the curvature dependence of surface tension shall be continued in § 3.5.
3.4. Control of surface tension
The present formulation allows us to select the surface tension in the simulation via the capillarity parameter ![]() $\kappa$, independently from the density ratio and temperature. To demonstrate this feature, flat interface simulations were performed at three reduced temperatures,
$\kappa$, independently from the density ratio and temperature. To demonstrate this feature, flat interface simulations were performed at three reduced temperatures, ![]() $T_r=\{0.99, 0.98, 0.97\}$, for different values of
$T_r=\{0.99, 0.98, 0.97\}$, for different values of ![]() $\tilde {\kappa }$. The surface tension was evaluated using (3.16). Results in figure 7 demonstrate that the surface tension can be effectively tuned using
$\tilde {\kappa }$. The surface tension was evaluated using (3.16). Results in figure 7 demonstrate that the surface tension can be effectively tuned using ![]() $\tilde {\kappa }$ and that changes in surface tension do not affect the equilibrium density ratios. This is further detailed in table 1 where the values of surface tension and deviations of the vapour and liquid densities from theoretical values are given as a function of
$\tilde {\kappa }$ and that changes in surface tension do not affect the equilibrium density ratios. This is further detailed in table 1 where the values of surface tension and deviations of the vapour and liquid densities from theoretical values are given as a function of ![]() $\tilde {\kappa }$ for
$\tilde {\kappa }$ for ![]() $T_r=0.97$. It is clearly observed that while the surface tension covers two orders of magnitude, the deviation from the predicted density of vapour is at most
$T_r=0.97$. It is clearly observed that while the surface tension covers two orders of magnitude, the deviation from the predicted density of vapour is at most ![]() $0.041$ percent. Furthermore, in the limit of vanishing
$0.041$ percent. Furthermore, in the limit of vanishing ![]() $\kappa$, the surface tension also vanishes, as expected from the theory, (3.15).
$\kappa$, the surface tension also vanishes, as expected from the theory, (3.15).

Figure 7. (a) Surface tension as a function of capillarity parameter ![]() $\tilde {\kappa }$; (b) liquid/vapour densities as a function of
$\tilde {\kappa }$; (b) liquid/vapour densities as a function of ![]() $\tilde {\kappa }$. Results of simulation shown at three different reduced temperatures: blue square,
$\tilde {\kappa }$. Results of simulation shown at three different reduced temperatures: blue square, ![]() $T_r=0.99$; red circles,
$T_r=0.99$; red circles, ![]() $T_r=0.98$; black triangles,
$T_r=0.98$; black triangles, ![]() $T_r=0.97$. Dashed grey lines, theoretical coexistence densities from the Maxwell construction.
$T_r=0.97$. Dashed grey lines, theoretical coexistence densities from the Maxwell construction.
Table 1. Effect of the choice of ![]() $\tilde {\kappa }$ on surface tension and deviations in equilibrium vapour and liquid phases densities for
$\tilde {\kappa }$ on surface tension and deviations in equilibrium vapour and liquid phases densities for ![]() $T_r=0.97$.
$T_r=0.97$.

3.5. Effect of curvature on surface tension: Tolman length
The drop simulation in § 3.3 made use of the Laplace law, relying on the equimolar dividing surface of radius ![]() $R_e$ in (3.21). Further discussion on the non-uniqueness of the choice of the dividing surface and the curvature dependence of surface tension is in order. Following Gibbs (Reference Gibbs1874), the free energy of a drop or bubble separated from the surrounding vapour or liquid by a dividing circle (
$R_e$ in (3.21). Further discussion on the non-uniqueness of the choice of the dividing surface and the curvature dependence of surface tension is in order. Following Gibbs (Reference Gibbs1874), the free energy of a drop or bubble separated from the surrounding vapour or liquid by a dividing circle (![]() $D=2$) or sphere (
$D=2$) or sphere (![]() $D=3$) of length or area
$D=3$) of length or area ![]() $\varSigma$ is
$\varSigma$ is ![]() $A=U-TS+\sigma \varSigma$, where
$A=U-TS+\sigma \varSigma$, where ![]() $U$ and
$U$ and ![]() $S$ are the internal energy and entropy of bulk phases while the last term is the adsorbance of free energy. The equilibrium condition requires vanishing of the variation
$S$ are the internal energy and entropy of bulk phases while the last term is the adsorbance of free energy. The equilibrium condition requires vanishing of the variation ![]() $\delta A$; for the isothermal case, we have
$\delta A$; for the isothermal case, we have
where ![]() $P_{l,v}$ and
$P_{l,v}$ and ![]() $P_{v,l}$ are the pressures inside and outside the liquid drop or vapour bubble. Using
$P_{v,l}$ are the pressures inside and outside the liquid drop or vapour bubble. Using ![]() $\delta V_{l,v}=-\delta V_{v,l}=2(D-1){\rm \pi} R^{D-1} \delta R$ and
$\delta V_{l,v}=-\delta V_{v,l}=2(D-1){\rm \pi} R^{D-1} \delta R$ and ![]() $\delta \varSigma =2(D-1)^2{\rm \pi} R^{D-2} \delta R$ leads to a generalized Laplace law,
$\delta \varSigma =2(D-1)^2{\rm \pi} R^{D-2} \delta R$ leads to a generalized Laplace law,
The derivative of surface tension ![]() ${\rm d}\sigma /{\rm d}R$ is termed a notional derivative by some authors (Blokhuis & Bedeaux Reference Blokhuis and Bedeaux1992) to stress that it refers to arbitrariness of the dividing surface. Apart from the equimolar surface in (3.21), the surface of tension is another possible choice to lift the ambiguity of the dividing surface. The notional derivative vanishes at the surface of tension,
${\rm d}\sigma /{\rm d}R$ is termed a notional derivative by some authors (Blokhuis & Bedeaux Reference Blokhuis and Bedeaux1992) to stress that it refers to arbitrariness of the dividing surface. Apart from the equimolar surface in (3.21), the surface of tension is another possible choice to lift the ambiguity of the dividing surface. The notional derivative vanishes at the surface of tension,
thereby reducing the generalized Laplace law in (3.23) to a standard form,
Integrating (3.23) from ![]() $R_s$ to
$R_s$ to ![]() $R$, and eliminating
$R$, and eliminating ![]() $\Delta P$ using (3.25), one obtains an analytic expression for the notional surface tension
$\Delta P$ using (3.25), one obtains an analytic expression for the notional surface tension ![]() $\sigma (R)$ relative to its minimum
$\sigma (R)$ relative to its minimum ![]() $\sigma _s$ at the surface of tension
$\sigma _s$ at the surface of tension ![]() $R_s$,
$R_s$,
Equation (3.26) provides for a simple way of identifying the surface of tension and the corresponding surface tension. Two-dimensional simulations at ![]() $T_r=0.98$ were conducted with different initial drop and bubble sizes,
$T_r=0.98$ were conducted with different initial drop and bubble sizes, ![]() $R_0\in \{30,40,50,60,70,80,100,120,140\}$. For each dividing surface of radius
$R_0\in \{30,40,50,60,70,80,100,120,140\}$. For each dividing surface of radius ![]() $R$, the corresponding surface tension was evaluated as (Blokhuis & Bedeaux Reference Blokhuis and Bedeaux1992)
$R$, the corresponding surface tension was evaluated as (Blokhuis & Bedeaux Reference Blokhuis and Bedeaux1992)
where ![]() $P_{\parallel }(r)$ is the tangential component of the pressure tensor, computed via the discrete pressure tensor detailed in Appendix E, and
$P_{\parallel }(r)$ is the tangential component of the pressure tensor, computed via the discrete pressure tensor detailed in Appendix E, and
is the normal pressure component in the sharp interface system, where ![]() $H$ is the Heaviside step function. For each drop or bubble, surface tension
$H$ is the Heaviside step function. For each drop or bubble, surface tension ![]() $\sigma (R)$ in (3.27) was probed at seventeen equidistant dividing circles between
$\sigma (R)$ in (3.27) was probed at seventeen equidistant dividing circles between ![]() $R_{min}=5\delta r$ and
$R_{min}=5\delta r$ and ![]() $R_{max}=165\delta r$. The discrete values
$R_{max}=165\delta r$. The discrete values ![]() $\sigma (R)$ obtained in these simulations were fitted with (3.26), with
$\sigma (R)$ obtained in these simulations were fitted with (3.26), with ![]() $\sigma _s$ and
$\sigma _s$ and ![]() $R_s$ as the free fitting parameters. Figure 8 shows that the data for all drops and bubbles collapsed on a single master curve are in excellent agreement with the theory in (3.26). Thus, the proposed model correctly identifies the surface of tension for the van der Waals fluid.
$R_s$ as the free fitting parameters. Figure 8 shows that the data for all drops and bubbles collapsed on a single master curve are in excellent agreement with the theory in (3.26). Thus, the proposed model correctly identifies the surface of tension for the van der Waals fluid.

Figure 8. Variation of surface tension ![]() $\sigma$ with the radius of the dividing circle
$\sigma$ with the radius of the dividing circle ![]() $R$ at
$R$ at ![]() $T_r=0.98$. Grey dashed line, theory in (3.26); symbol, simulations with van der Waals equation of state; blue circles, drop simulations; red diamonds, bubble simulations. Shading from dark to light, drops and bubbles of increasing sizes are shown.
$T_r=0.98$. Grey dashed line, theory in (3.26); symbol, simulations with van der Waals equation of state; blue circles, drop simulations; red diamonds, bubble simulations. Shading from dark to light, drops and bubbles of increasing sizes are shown.
While the notional derivative ![]() ${\rm d}\sigma (R)/{\rm d}R$ vanishes at the surface of tension, the same does not hold for the surface tension at the surface of tension,
${\rm d}\sigma (R)/{\rm d}R$ vanishes at the surface of tension, the same does not hold for the surface tension at the surface of tension, ![]() ${\rm d}\sigma _s/{\rm d}R_s\neq 0$. In other words, surface tension
${\rm d}\sigma _s/{\rm d}R_s\neq 0$. In other words, surface tension ![]() $\sigma _s$ depends on the curvature of the surface of tension. In a seminal paper, Tolman (Reference Tolman1949) characterized the curvature dependence of surface tension by the Tolman length. For sufficiently large
$\sigma _s$ depends on the curvature of the surface of tension. In a seminal paper, Tolman (Reference Tolman1949) characterized the curvature dependence of surface tension by the Tolman length. For sufficiently large ![]() $R_s$, the leading-order curvature dependence of the surface tension may be written as (Tolman Reference Tolman1949)
$R_s$, the leading-order curvature dependence of the surface tension may be written as (Tolman Reference Tolman1949)
where ![]() $\delta _T$ is the Tolman length and
$\delta _T$ is the Tolman length and ![]() $\sigma _0$ is the flat interface surface tension coefficient. Here, the negative (positive) sign corresponds to drops (bubbles).
$\sigma _0$ is the flat interface surface tension coefficient. Here, the negative (positive) sign corresponds to drops (bubbles).
We first compare the leading-order Tolman model in (3.29) with the simulation. The values of ![]() $R_s$ obtained in the previously described drops and bubbles simulations of figure 8 are plotted against the pressure difference for different drop and bubble sizes in figure 9. It is clear that for smaller drops and bubbles, the pressure difference deviates from the Laplace law with constant
$R_s$ obtained in the previously described drops and bubbles simulations of figure 8 are plotted against the pressure difference for different drop and bubble sizes in figure 9. It is clear that for smaller drops and bubbles, the pressure difference deviates from the Laplace law with constant ![]() $\sigma _s=\sigma _0$, indicating a curvature-dependent surface tension. Fitting the data points with (3.29), the Tolman length can be extracted from the simulation, here
$\sigma _s=\sigma _0$, indicating a curvature-dependent surface tension. Fitting the data points with (3.29), the Tolman length can be extracted from the simulation, here ![]() $\delta _T=9\delta r$ for both drops and bubbles, at the reduced temperature
$\delta _T=9\delta r$ for both drops and bubbles, at the reduced temperature ![]() $T_r=0.98$.
$T_r=0.98$.

Figure 9. Pressure difference scaling with surface of tension radius ![]() $R_s$ for liquid drops and vapour bubbles. Symbol, simulation data for van der Waals equation of state with
$R_s$ for liquid drops and vapour bubbles. Symbol, simulation data for van der Waals equation of state with ![]() $a=0.18$ and
$a=0.18$ and ![]() $b=0.095$l; black line, Laplace law with
$b=0.095$l; black line, Laplace law with ![]() $\sigma =\sigma _0$; blue lines, best fit with (3.29) used to compute Tolman length
$\sigma =\sigma _0$; blue lines, best fit with (3.29) used to compute Tolman length ![]() $\delta _T$; red lines, best fit with the second-order Helfrich expansion in (3.30).
$\delta _T$; red lines, best fit with the second-order Helfrich expansion in (3.30).
While the leading-order Tolman correction in (3.29) improves the agreement with data at moderate ![]() $R_s$, deviation persists for smaller drops and bubbles at
$R_s$, deviation persists for smaller drops and bubbles at ![]() $\delta r/R_s> 0.03$. Higher-order terms in the inverse powers of
$\delta r/R_s> 0.03$. Higher-order terms in the inverse powers of ![]() $R_s$, important for droplets or bubbles of small radius, are neglected by (3.29) and are addressed by Helfrich (Reference Helfrich1978)
$R_s$, important for droplets or bubbles of small radius, are neglected by (3.29) and are addressed by Helfrich (Reference Helfrich1978)
where ![]() $k$ and
$k$ and ![]() $\bar {k}$ are the bending and Gaussian rigidities; note that the latter vanishes for
$\bar {k}$ are the bending and Gaussian rigidities; note that the latter vanishes for ![]() $D=2$. Taking the second-order term in (3.30) into account, the best fit in figure 9 results in bending rigidity
$D=2$. Taking the second-order term in (3.30) into account, the best fit in figure 9 results in bending rigidity ![]() $k=1.049\times 10^{5}\sigma _0\delta r^2$.
$k=1.049\times 10^{5}\sigma _0\delta r^2$.
Finally we consider the limit of a flat interface where the Tolman length can be derived independently from the above considerations. In this case, the location of the surface of tension ![]() $X_s$ can be found as the normalized first-order moment of the normal stress difference (Rao & Berne Reference Rao and Berne1979),
$X_s$ can be found as the normalized first-order moment of the normal stress difference (Rao & Berne Reference Rao and Berne1979),
 \begin{equation} X_s = \frac{\displaystyle\int_{-\infty}^{\infty} x(P_{xx} - P_{yy})\, {\rm d} x}{\displaystyle\int_{-\infty}^{\infty} (P_{xx} - P_{yy}) \,{\rm d} x}. \end{equation}
\begin{equation} X_s = \frac{\displaystyle\int_{-\infty}^{\infty} x(P_{xx} - P_{yy})\, {\rm d} x}{\displaystyle\int_{-\infty}^{\infty} (P_{xx} - P_{yy}) \,{\rm d} x}. \end{equation}
With the dividing surface as a vertical straight line at ![]() $X$ in two dimensions, the mass adsorbance
$X$ in two dimensions, the mass adsorbance ![]() $\varGamma (X)$ is defined as (see example in figure 10)
$\varGamma (X)$ is defined as (see example in figure 10)
Similar to the case of cylindrical symmetry considered in § 3.3, the equimolar surface is found by annihilating the mass adsorbance, ![]() $\varGamma (X_e)=0$.
$\varGamma (X_e)=0$.

Figure 10. Example of mass adsorbance for a flat interface. Black continuous line, density profile at ![]() $T_r=0.98$; red dashed line, sharp interface profile with the dividing surface at
$T_r=0.98$; red dashed line, sharp interface profile with the dividing surface at ![]() $X/\delta r=70$. Grey area represents the mass adsorbance
$X/\delta r=70$. Grey area represents the mass adsorbance ![]() $\varGamma (X)$ in (3.32).
$\varGamma (X)$ in (3.32).
The Tolman length in the limit of the flat interface is the distance between the surface of tension and the equimolar surface (Blokhuis & Bedeaux Reference Blokhuis and Bedeaux1992; Blokhuis & Kuipers Reference Blokhuis and Kuipers2006),
An example from the simulation is presented in figure 11. As shown by Blokhuis & Bedeaux (Reference Blokhuis and Bedeaux1992), the Tolman length scales with the reduced temperature as
To validate the scaling of (3.34) in our model, flat interface simulations were conducted over a range of temperatures in the vicinity of the critical state. The Tolman length in (3.33) for various temperatures is shown in figure 11. The results obtained from simulations are in excellent agreement with the theoretical scaling by (3.34). A similar study using the Shan–Chen equations of states and the pseudo-potential model was presented in (Lulli et al. Reference Lulli, Biferale, Falcucci, Sbragaglia and Shan2021). Furthermore, the flat interface simulations lead to a ![]() $\delta _T=9.2\delta r$ at
$\delta _T=9.2\delta r$ at ![]() $T_r=0.98$, in agreement with the value obtained from drop and bubble simulations,
$T_r=0.98$, in agreement with the value obtained from drop and bubble simulations, ![]() $\delta _T=9\delta r$ at the same temperature. The relatively small discrepancy can be attributed to higher-order terms in the curvature, neglected in the fitting process.
$\delta _T=9\delta r$ at the same temperature. The relatively small discrepancy can be attributed to higher-order terms in the curvature, neglected in the fitting process.

Figure 11. (a) Temperature dependence of Tolman length ![]() $\delta _T$. Results from the flat interface simulation for van der Waals fluid are shown with blue squares while the grey dashed line represents theoretical scaling by (3.34). (b) Surface of tension, equimolar surface and Tolman length for a flat interface. Continuous black line, density profile at
$\delta _T$. Results from the flat interface simulation for van der Waals fluid are shown with blue squares while the grey dashed line represents theoretical scaling by (3.34). (b) Surface of tension, equimolar surface and Tolman length for a flat interface. Continuous black line, density profile at ![]() $T_r=0.98$; red dashed line, sharp approximation with the equimolar surface as the dividing surface; blue dotted line, sharp approximation with the surface of tension as the dividing surface. Distance between the surface of tension and the equimolar surface is the Tolman length. In all simulations,
$T_r=0.98$; red dashed line, sharp approximation with the equimolar surface as the dividing surface; blue dotted line, sharp approximation with the surface of tension as the dividing surface. Distance between the surface of tension and the equimolar surface is the Tolman length. In all simulations, ![]() $a=0.18$ and
$a=0.18$ and ![]() $b=0.095$.
$b=0.095$.
3.6. Interface width: temperature scaling and control
In the present work, we use a definition for the interface width bearing numerical information as to how well the stiff gradients are resolved on a given mesh, making it directly related to the velocity increment per time step:
where ![]() $\rho _l$ and
$\rho _l$ and ![]() $\rho _v$ are the densities of saturated liquid and vapour, respectively. It can readily be observed that in the limit of a sharp interface, i.e. resolved with
$\rho _v$ are the densities of saturated liquid and vapour, respectively. It can readily be observed that in the limit of a sharp interface, i.e. resolved with ![]() $\delta r$,
$\delta r$, ![]() $\delta r/W\to 1$. As previously noted for the co-existence densities and surface tension, the model recovers thermodynamical properties/scalings of the second-gradient fluid in the limit
$\delta r/W\to 1$. As previously noted for the co-existence densities and surface tension, the model recovers thermodynamical properties/scalings of the second-gradient fluid in the limit ![]() $\varepsilon \to 0$, akin to
$\varepsilon \to 0$, akin to ![]() $\delta r/W\to 0$. As such, in the limit of
$\delta r/W\to 0$. As such, in the limit of ![]() $\delta r/W \to 1$, one expects numerical effects to dominate and observe deviations from thermodynamics of the van der Waals fluid.
$\delta r/W \to 1$, one expects numerical effects to dominate and observe deviations from thermodynamics of the van der Waals fluid.
Surface tension vanishes as the temperature approaches the critical, cf. § 3.3, (3.15) and figure 6, while the interface diverges as ![]() $T\to T_c$. As noted by Widom (Reference Widom1965), the van der Waals theory predicts the temperature scaling of the interface width as
$T\to T_c$. As noted by Widom (Reference Widom1965), the van der Waals theory predicts the temperature scaling of the interface width as
To validate the consistency of the proposed model, simulations of flat interfaces were carried out in a range of reduced temperatures ![]() $T_r$ near the critical point, and corresponding interface widths
$T_r$ near the critical point, and corresponding interface widths ![]() $W(T_r)$ in (3.35) were measured. Given the effect of the choice of
$W(T_r)$ in (3.35) were measured. Given the effect of the choice of ![]() $a$ on interface thickness, simulations were also carried out with different
$a$ on interface thickness, simulations were also carried out with different ![]() $a$. The results obtained from simulations near the critical point are shown in figure 12. As noted by many authors in the literature (Jamet et al. Reference Jamet, Lebaigue, Coutris and Delhaye2001), the parameter
$a$. The results obtained from simulations near the critical point are shown in figure 12. As noted by many authors in the literature (Jamet et al. Reference Jamet, Lebaigue, Coutris and Delhaye2001), the parameter ![]() $a$ can be used to control the interface thickness, as done in the present work, at a given density ratio, leaving the ratios and Maxwell construction unaffected. In agreement with the equivalent states theory, the right-hand side plot in figure 12 points to the universality of the scaling of the interface width near the critical point regardless of the choice of
$a$ can be used to control the interface thickness, as done in the present work, at a given density ratio, leaving the ratios and Maxwell construction unaffected. In agreement with the equivalent states theory, the right-hand side plot in figure 12 points to the universality of the scaling of the interface width near the critical point regardless of the choice of ![]() $a$. In addition, it is interesting to note that for a fixed grid-size
$a$. In addition, it is interesting to note that for a fixed grid-size ![]() $\delta r$, as
$\delta r$, as ![]() $(1-T_r)\to 1$,
$(1-T_r)\to 1$, ![]() $\delta r/W\to 1$ (equivalent to the scaling parameter
$\delta r/W\to 1$ (equivalent to the scaling parameter ![]() $\varepsilon$ introduced in the multi-scale analysis), indicating deviation from the thermodynamically converged state. This is illustrated by the deviation of the numerical interface thickness, starting at
$\varepsilon$ introduced in the multi-scale analysis), indicating deviation from the thermodynamically converged state. This is illustrated by the deviation of the numerical interface thickness, starting at ![]() $T_r\approx 0.98$ from the theoretical predictions. Lowering the value of
$T_r\approx 0.98$ from the theoretical predictions. Lowering the value of ![]() $a$, i.e. rescaling the interface by a factor
$a$, i.e. rescaling the interface by a factor ![]() $1/\sqrt {a}$ and therefore lowering
$1/\sqrt {a}$ and therefore lowering ![]() $\varepsilon$, it is observed that interface is again well resolved and the scaling in (3.36) is restored. In agreement with previous sections, in the limit of
$\varepsilon$, it is observed that interface is again well resolved and the scaling in (3.36) is restored. In agreement with previous sections, in the limit of ![]() $\varepsilon \to 0$, the model is shown to be thermodynamically converged and recovers the properties of the second-gradient fluid.
$\varepsilon \to 0$, the model is shown to be thermodynamically converged and recovers the properties of the second-gradient fluid.

Figure 12. (a) Interface width as a function of temperature. Blue square, simulation with ![]() $a=0.184$; red circle, simulation with
$a=0.184$; red circle, simulation with ![]() $a=0.02$; grey dashed line, theoretical scaling by (3.36). (b) Effect of the choice of
$a=0.02$; grey dashed line, theoretical scaling by (3.36). (b) Effect of the choice of ![]() $a$ on the interface width. Simulation for
$a$ on the interface width. Simulation for ![]() $T_r= 0.98$ (diamond), 0.99 (square), 0.995 (circle).
$T_r= 0.98$ (diamond), 0.99 (square), 0.995 (circle).
4. Hydrodynamic consistency
4.1. Shear stress: layered Poiseuille flow
The setup consists of a rectangular domain filled with the liquid phase at the bottom and the vapour phase on top. The flow is driven by a body force. Top and bottom are subject to no-slip boundary conditions while the inlet and outlet are fixed by periodicity. The momentum balance at the steady state reduces to a well-posed system of ordinary differential equations,
closed by the following boundary conditions:
Here ![]() $H$ is the height of the channel,
$H$ is the height of the channel, ![]() $h_l$ the height of the section filled with the liquid phase,
$h_l$ the height of the section filled with the liquid phase, ![]() $\mu _l$ and
$\mu _l$ and ![]() $\mu _v$ are the dynamic viscosities of the liquid and vapour, respectively, and
$\mu _v$ are the dynamic viscosities of the liquid and vapour, respectively, and ![]() $g$ is the acceleration due to the body force. An analytical solution is given in Appendix F. This configuration is of particular interest as it probes the ability of a two-phase model to capture jump conditions at the interface which happens only if deviatoric components of the viscous stress tensor in (2.11) are correctly recovered.
$g$ is the acceleration due to the body force. An analytical solution is given in Appendix F. This configuration is of particular interest as it probes the ability of a two-phase model to capture jump conditions at the interface which happens only if deviatoric components of the viscous stress tensor in (2.11) are correctly recovered.
Two sets of parameters were considered: (a) ![]() $\mu _l/\mu _v=10.1$,
$\mu _l/\mu _v=10.1$, ![]() $\rho _l/\rho _v=10.1$ (
$\rho _l/\rho _v=10.1$ (![]() $T_r=0.77$) and (b)
$T_r=0.77$) and (b) ![]() $\mu _l/\mu _v=11.3$,
$\mu _l/\mu _v=11.3$, ![]() $\rho _l/\rho _v=1030$ (
$\rho _l/\rho _v=1030$ (![]() $T_r=0.36$). Simulations were conducted on a grid of size
$T_r=0.36$). Simulations were conducted on a grid of size ![]() $5\times 200$, with a constant acceleration
$5\times 200$, with a constant acceleration ![]() $g=10^{-8}\delta r/\delta t^2$. Furthermore, the same simulations were performed with the conventional second-order equilibrium (Succi Reference Succi2002) instead of the product form in (2.54). The steady-state results are compared to the analytical solution in figure 13. In contrast to the conventional second-order equilibrium, the use of the product form of (2.54) in our model recovers the correct jump conditions and therefore results in continuous velocity profiles, also for a large density ratio, in excellent agreement with analytical solution. A look at the maximum non-dimensional velocities in the domains, respectively
$g=10^{-8}\delta r/\delta t^2$. Furthermore, the same simulations were performed with the conventional second-order equilibrium (Succi Reference Succi2002) instead of the product form in (2.54). The steady-state results are compared to the analytical solution in figure 13. In contrast to the conventional second-order equilibrium, the use of the product form of (2.54) in our model recovers the correct jump conditions and therefore results in continuous velocity profiles, also for a large density ratio, in excellent agreement with analytical solution. A look at the maximum non-dimensional velocities in the domains, respectively ![]() $5\times 10^{-4}$ and
$5\times 10^{-4}$ and ![]() $0.04$ for density ratios 10 and 1000, further shows that in contrast to single-phase flows where deviations become only important for large non-dimensional velocities, here, due to the presence of large density gradients at the interfaces, third-order contributions to the equilibrium must be retained even for small velocities.
$0.04$ for density ratios 10 and 1000, further shows that in contrast to single-phase flows where deviations become only important for large non-dimensional velocities, here, due to the presence of large density gradients at the interfaces, third-order contributions to the equilibrium must be retained even for small velocities.

Figure 13. Steady-state velocity profiles for the layered Poiseuille flow. Configuration (a) is where ![]() $T_r=0.77$,
$T_r=0.77$, ![]() $\rho _l/\rho _v=10.1$,
$\rho _l/\rho _v=10.1$, ![]() $\mu _l/\mu _v=10.1$. Configuration (b) is where
$\mu _l/\mu _v=10.1$. Configuration (b) is where ![]() $T_r=0.36$,
$T_r=0.36$, ![]() $\rho _l/\rho _v=1030$ and
$\rho _l/\rho _v=1030$ and ![]() $\mu _l/\mu _v=11.3$. Grey plain line, analytical solution; black dashed line, LBM with product-form equilibrium; red dashed line, LBM with conventional second-order equilibrium.
$\mu _l/\mu _v=11.3$. Grey plain line, analytical solution; black dashed line, LBM with product-form equilibrium; red dashed line, LBM with conventional second-order equilibrium.
4.2. Normal stress: dissipation of acoustic waves
To assess Galilean invariance of the diagonal components of the viscous stress tensor and the effect of the correction term, the dissipation of acoustic waves was measured numerically. Acoustic waves were initialized as a small perturbation of density with an amplitude ![]() $\delta \rho$ and subject to uniform background velocity
$\delta \rho$ and subject to uniform background velocity ![]() $U_0$ representing a moving reference frame,
$U_0$ representing a moving reference frame,
where ![]() $\rho _0$ is the density of saturated liquid or vapour at a given temperature and
$\rho _0$ is the density of saturated liquid or vapour at a given temperature and ![]() $\lambda$ is the wavelength of the perturbation. The maximum velocity in the domain was monitored over time and fitted to an exponential function of the form
$\lambda$ is the wavelength of the perturbation. The maximum velocity in the domain was monitored over time and fitted to an exponential function of the form ![]() $\max (u) - U_0 = \exp (-\varLambda t)$, where the coefficient
$\max (u) - U_0 = \exp (-\varLambda t)$, where the coefficient ![]() $\varLambda$ is tied to the dissipation rate of the normal modes as
$\varLambda$ is tied to the dissipation rate of the normal modes as
Simulations were performed on a periodic domain of size ![]() $L=128\delta r\times \delta r$ with
$L=128\delta r\times \delta r$ with ![]() $\lambda =64\delta r$ at the temperature
$\lambda =64\delta r$ at the temperature ![]() $T_r=0.36$, corresponding to a density ratio
$T_r=0.36$, corresponding to a density ratio ![]() $\rho _l/\rho _v\approx 10^3$. The perturbation amplitude was set to
$\rho _l/\rho _v\approx 10^3$. The perturbation amplitude was set to ![]() $\delta \rho = 10^{-4}\rho _0$ while the reference frame velocity varied in the range
$\delta \rho = 10^{-4}\rho _0$ while the reference frame velocity varied in the range ![]() $U_0\delta t/\delta r\in [0, 0.3]$. The dissipation rate from (4.4) with and without the correction term are shown in figure 14. It is observed that the correction term for the third-order diagonal moments of the equilibrium populations in (2.58) restores the Galilean invariance (independence from the reference frame velocity) of the dissipation rate of normal modes.
$U_0\delta t/\delta r\in [0, 0.3]$. The dissipation rate from (4.4) with and without the correction term are shown in figure 14. It is observed that the correction term for the third-order diagonal moments of the equilibrium populations in (2.58) restores the Galilean invariance (independence from the reference frame velocity) of the dissipation rate of normal modes.

Figure 14. Dissipation rate of acoustic mode at ![]() $T_r=0.36$. Circle, saturated liquid; triangle, saturated vapour. Blue, simulation of the model with the correction term; red, simulation of the model without the correction term.
$T_r=0.36$. Circle, saturated liquid; triangle, saturated vapour. Blue, simulation of the model with the correction term; red, simulation of the model without the correction term.
4.3. Viscosity-capillarity coupling: oscillating drop
Rayleigh's classical study of a freely oscillating drop of non-viscous liquid under small deformations laid ground for the understanding of capillary waves (Rayleigh Reference Rayleigh1879). Assuming purely axisymmetric oscillation modes, Rayleigh's oscillation frequency of the ![]() $n$th mode,
$n$th mode, ![]() $n=2,3,\dots$, for large density ratios,
$n=2,3,\dots$, for large density ratios, ![]() $\rho _l/\rho _v\gg 1$, is given by
$\rho _l/\rho _v\gg 1$, is given by
 \begin{equation} f_n = \frac{1}{2{\rm \pi}}\sqrt{\frac{\sigma n (n-1)(n+2)}{\rho_l R_0^3}}. \end{equation}
\begin{equation} f_n = \frac{1}{2{\rm \pi}}\sqrt{\frac{\sigma n (n-1)(n+2)}{\rho_l R_0^3}}. \end{equation}
Two-dimensional simulations were performed for a drop of initial radius ![]() $R_0=40\delta r$, for a relatively low kinematic viscosity,
$R_0=40\delta r$, for a relatively low kinematic viscosity, ![]() $\nu _l\delta t/\delta r^2=0.01$. Modes of order
$\nu _l\delta t/\delta r^2=0.01$. Modes of order ![]() $n=2,3,4,5,6$ were initiated with a monochromatic perturbation,
$n=2,3,4,5,6$ were initiated with a monochromatic perturbation, ![]() $R(\theta,0)=R_0(1 + a_n \cos (n\theta ) - \frac {1}{4}na_n^2)$, with the amplitude
$R(\theta,0)=R_0(1 + a_n \cos (n\theta ) - \frac {1}{4}na_n^2)$, with the amplitude ![]() $a_n=0.1$. The reduced temperature of the van der Waals fluid was set to
$a_n=0.1$. The reduced temperature of the van der Waals fluid was set to ![]() $T_r=0.36$, corresponding to a density ratio
$T_r=0.36$, corresponding to a density ratio ![]() $\rho _l/\rho _v\approx 10^3$. The initial and mid-cycle shapes of Rayleigh's modes are shown in figure 15. Simulations were performed over eight oscillation cycles and corresponding oscillation periods were identified. Figure 15 demonstrates an excellent comparison of the oscillation frequencies measured in the simulation with the corresponding theoretical values from (4.5), even for higher-order modes. While Rayleigh's analysis was restricted to non-viscous liquids, a number of analytical solutions for viscous oscillating drops have been obtained over the years. In particular, Aalilija, Gandin & Hachem (Reference Aalilija, Gandin and Hachem2020) derived a time-dependent solution of the following form:
$\rho _l/\rho _v\approx 10^3$. The initial and mid-cycle shapes of Rayleigh's modes are shown in figure 15. Simulations were performed over eight oscillation cycles and corresponding oscillation periods were identified. Figure 15 demonstrates an excellent comparison of the oscillation frequencies measured in the simulation with the corresponding theoretical values from (4.5), even for higher-order modes. While Rayleigh's analysis was restricted to non-viscous liquids, a number of analytical solutions for viscous oscillating drops have been obtained over the years. In particular, Aalilija, Gandin & Hachem (Reference Aalilija, Gandin and Hachem2020) derived a time-dependent solution of the following form:
where ![]() $\epsilon _n = a_n \exp (-\lambda _n t) \cos (2{\rm \pi} f_n t)$, while
$\epsilon _n = a_n \exp (-\lambda _n t) \cos (2{\rm \pi} f_n t)$, while ![]() $\lambda _n$ is the damping rate of the
$\lambda _n$ is the damping rate of the ![]() $n$th mode,
$n$th mode,

Figure 15. (a) Drop oscillation period for modes ![]() $n=2,3,4,5,6$. Red circle, simulation; blue square, Rayleigh's modes from (4.5). (b) Corresponding shapes of the drop at
$n=2,3,4,5,6$. Red circle, simulation; blue square, Rayleigh's modes from (4.5). (b) Corresponding shapes of the drop at ![]() $t=1/2\delta t f_n$ and
$t=1/2\delta t f_n$ and ![]() $t=1/\delta t f_n$.
$t=1/\delta t f_n$.
To validate the damping rate of capillary waves, the previously described two-dimensional drop was simulated in a range of kinematic viscosities, ![]() $\nu _l\delta t/\delta r^2\in [0.01, 0.1]$, subject to a monochromatic perturbation with the lowest mode
$\nu _l\delta t/\delta r^2\in [0.01, 0.1]$, subject to a monochromatic perturbation with the lowest mode ![]() $n=2$ and the initial perturbation amplitude was set to
$n=2$ and the initial perturbation amplitude was set to ![]() $a_2=0.2$. The envelope of oscillations was fitted using the exponential function
$a_2=0.2$. The envelope of oscillations was fitted using the exponential function ![]() $\exp (-\varLambda t)$, see figure 16. The effective damping coefficient
$\exp (-\varLambda t)$, see figure 16. The effective damping coefficient ![]() $\varLambda$ was used along with (4.7) to evaluate the apparent kinematic viscosity. As shown in figure 16, the dissipation rates obtained by simulation agree well with the analytical solution from (4.7).
$\varLambda$ was used along with (4.7) to evaluate the apparent kinematic viscosity. As shown in figure 16, the dissipation rates obtained by simulation agree well with the analytical solution from (4.7).

Figure 16. (a) Time evolution of the drop radius in directions ![]() $\theta =0$ and
$\theta =0$ and ![]() $\theta ={\rm \pi} /2$ for kinematic viscosity
$\theta ={\rm \pi} /2$ for kinematic viscosity ![]() $\nu \delta t/\delta r^2=0.02$. Grey line, analytical solution from (4.6); symbol: simulation; dashed black line, the
$\nu \delta t/\delta r^2=0.02$. Grey line, analytical solution from (4.6); symbol: simulation; dashed black line, the ![]() $\exp (-\varLambda t)$ fit used to compute the dissipation rate in (4.7). (b) Apparent viscosity as computed via (4.7). Grey line, analytical solution from (4.7); symbol, simulation. All results correspond to the oscillation mode
$\exp (-\varLambda t)$ fit used to compute the dissipation rate in (4.7). (b) Apparent viscosity as computed via (4.7). Grey line, analytical solution from (4.7); symbol, simulation. All results correspond to the oscillation mode ![]() $n=2$.
$n=2$.
4.4. Isothermal speed of sound
Finally, we validate the speed of sound at different temperatures in both the liquid and vapour phases. For the van der Waals fluid, the isothermal sound speed is
 \begin{equation} c_s = \sqrt{\frac{\partial P}{\partial \rho}\bigg|_{T}} = \sqrt{\frac{RT}{{(b\rho-1)}^2} - 2a\rho}. \end{equation}
\begin{equation} c_s = \sqrt{\frac{\partial P}{\partial \rho}\bigg|_{T}} = \sqrt{\frac{RT}{{(b\rho-1)}^2} - 2a\rho}. \end{equation}
The sound speed was measured by monitoring the position of a pressure front over time in a quasi-one-dimensional simulation at different temperatures. The obtained results are compared to theory using (4.8) in figure 17. It is observed that the simulations accurately capture the speed of sound in both liquid and vapour phases, for the entire range of density ratios on the coexistence diagram in figure 2, up to at least ![]() $\rho _l/\rho _v\sim 10^{11}$. Results for other equations of state are compared in Appendix G.
$\rho _l/\rho _v\sim 10^{11}$. Results for other equations of state are compared in Appendix G.

Figure 17. Isothermal sound speed for van der Waals fluid at various temperatures. Line, theory using (4.8); symbol, simulation. Upper branch, saturated liquid; lower branch, saturated vapour.
4.5. Interaction with solid boundaries: equilibrium contact angle
A comprehensive review of various implementations of the contact angle on solid boundaries in the lattice Boltzmann setting can be found in Li et al. (Reference Li, Luo, Kang and Chen2014). Here we follow a proposal by Benzi et al. (Reference Benzi, Biferale, Sbragaglia, Succi and Toschi2006) where a virtual density, and therefore a corresponding virtual pseudo-potential, is attributed to the solid nodes. The calculations of the force using (2.69) are then carried at all fluid nodes. The no-slip condition is imposed via the modified bounce-back scheme of Bouzidi, Firdaouss & Lallemand (Reference Bouzidi, Firdaouss and Lallemand2001) for curved boundaries. The virtual density attributed to the solid nodes is the free parameters controlling the contact angle. The ability of this approach to correctly reproduce the dynamics of the contact line in a high-density ratio regime will be validated below.
4.5.1. Young–Laplace equation
As a first validation of the solid/fluid interaction, the case of a two-dimensional channel of height ![]() $H$ and length
$H$ and length ![]() $L$ is considered. Initially a rectangular column of liquid of length
$L$ is considered. Initially a rectangular column of liquid of length ![]() $L/3$ and height
$L/3$ and height ![]() $H$ surrounded by vapour was placed at the centre of the channel. Simulations were performed until the system reaches steady state, and the angle between the liquid/vapour interface and the solid wall at the triple-point was measured. The static contact angle measured at the triple-point should verify the Young–Laplace law for this configuration:
$H$ surrounded by vapour was placed at the centre of the channel. Simulations were performed until the system reaches steady state, and the angle between the liquid/vapour interface and the solid wall at the triple-point was measured. The static contact angle measured at the triple-point should verify the Young–Laplace law for this configuration:
where ![]() $\theta$ is the equilibrium contact angle and
$\theta$ is the equilibrium contact angle and ![]() $\sigma$ the liquid/vapour surface tension.
$\sigma$ the liquid/vapour surface tension.
Here, to validate the static angle, the reduced temperature of van der Waals fluid was set to ![]() $T_r=0.36$, which corresponds to a density ratio
$T_r=0.36$, which corresponds to a density ratio ![]() $\rho _l/\rho _v=10^3$. The height of the channel is set to
$\rho _l/\rho _v=10^3$. The height of the channel is set to ![]() $H=75\delta r$ and the length to
$H=75\delta r$ and the length to ![]() $L=300\delta r$. The pressure difference
$L=300\delta r$. The pressure difference ![]() $\Delta P$ is computed as the difference in pressure between two monitoring points located respectively inside and outside the liquid column. The convergence criterion used to assess steady state is based on the time variations of pressure at these two monitoring points. The contact angles were measured using the low-bond axisymmetric drop shape analysis module (Stalder et al. Reference Stalder, Melchior, Müller, Sage, Blu and Unser2010) in ImageJ. The results obtained for the entire contact angle range are shown in figure 18. The measured contact angles show excellent agreement with the Young–Laplace equation. Furthermore, the results show that for
$\Delta P$ is computed as the difference in pressure between two monitoring points located respectively inside and outside the liquid column. The convergence criterion used to assess steady state is based on the time variations of pressure at these two monitoring points. The contact angles were measured using the low-bond axisymmetric drop shape analysis module (Stalder et al. Reference Stalder, Melchior, Müller, Sage, Blu and Unser2010) in ImageJ. The results obtained for the entire contact angle range are shown in figure 18. The measured contact angles show excellent agreement with the Young–Laplace equation. Furthermore, the results show that for ![]() $\rho _w\to \rho _v$, the contact angle tends to
$\rho _w\to \rho _v$, the contact angle tends to ![]() $\theta \to 180^{\circ }$, while as
$\theta \to 180^{\circ }$, while as ![]() $\rho _w\to \rho _l$, the contact angles tend to
$\rho _w\to \rho _l$, the contact angles tend to ![]() $\theta \to 0^{\circ }$ therefore covering the entire range of contact angles.
$\theta \to 0^{\circ }$ therefore covering the entire range of contact angles.

Figure 18. Static contact angles as (blue squares) obtained from the Young–Laplace equation and (red circles) measured directly from the simulations.
4.5.2. Wettability-driven drop motion in a channel
A difference in contact angle on opposite sides of a liquid drop placed on a surface with a non-uniform wettability may initiate a motion of the drop. As a further validation of the solid/liquid interaction of the proposed model, the case of a liquid column placed in a channel and subjected to a wettability step function is considered. The configuration, illustrated in figure 19, consists of a channel of length ![]() $L$ and width/height of
$L$ and width/height of ![]() $H$. Initially a liquid column of length
$H$. Initially a liquid column of length ![]() $L_l$ is placed at the channel centre. Once the liquid column has reached equilibrium, the wettability on the right-half of the channel is changed, which results in unequal contact angles on the different sides of the liquid column. An approximate analytical solution for the centre-of-mass position
$L_l$ is placed at the channel centre. Once the liquid column has reached equilibrium, the wettability on the right-half of the channel is changed, which results in unequal contact angles on the different sides of the liquid column. An approximate analytical solution for the centre-of-mass position ![]() $X$ and centroid velocity
$X$ and centroid velocity ![]() $U$ was found by Esmaili, Moosavi & Mazloomi (Reference Esmaili, Moosavi and Mazloomi2012),
$U$ was found by Esmaili, Moosavi & Mazloomi (Reference Esmaili, Moosavi and Mazloomi2012),
where the saturated centroid velocity ![]() $U_{\infty }$ and transition time
$U_{\infty }$ and transition time ![]() $\tau _{\infty }$ are computed respectively as
$\tau _{\infty }$ are computed respectively as
Here, ![]() $H=70\delta r$ while
$H=70\delta r$ while ![]() $L=1260\delta r$,
$L=1260\delta r$, ![]() $L_l=420\delta r$,
$L_l=420\delta r$, ![]() $\nu _l=\nu _v=0.075\delta r^2/\delta t$ and the density ratio is set to
$\nu _l=\nu _v=0.075\delta r^2/\delta t$ and the density ratio is set to ![]() $10^3$ as in the previous cases. Initially, the contact angles on both sides of the water column were set to
$10^3$ as in the previous cases. Initially, the contact angles on both sides of the water column were set to ![]() $\theta ^{-}=59.3^{\circ }$. Once a steady state was reached, the contact angle on the right-hand side of the column was changed to
$\theta ^{-}=59.3^{\circ }$. Once a steady state was reached, the contact angle on the right-hand side of the column was changed to ![]() $\theta ^{+}=63.4^{\circ }$, which resulted in a net force acting on the liquid. The liquid column centroid velocity and centre-of-mass position are compared to the analytical solutions in figure 20. Both quantities closely match analytical predictions.
$\theta ^{+}=63.4^{\circ }$, which resulted in a net force acting on the liquid. The liquid column centroid velocity and centre-of-mass position are compared to the analytical solutions in figure 20. Both quantities closely match analytical predictions.

Figure 19. Schematics of the wettability-driven liquid column. Arrow indicates the direction of motion of the liquid column when the contact angle ![]() $\theta _{+}$ (right) exceeds the contact angle
$\theta _{+}$ (right) exceeds the contact angle ![]() $\theta _{-}$ (left).
$\theta _{-}$ (left).

Figure 20. (a) Centroid velocity and (b) centre-of-mass position as obtained from (grey line) analytical solution and (red markers) LB simulations for the wettability-driven motion case.
5. Application to the dynamic cases
5.1. Thermodynamic convergence and resolution requirements
Two-phase lattice Boltzmann models are routinely used to simulate the impact of liquid drops on solids. While experiments are typically conducted with water and other liquids in air, the applicability of the two-phase LBM is justified whenever the dynamic effects are concerned. However, the majority of LB models do not reach the experimentally relevant density ratios of, say, the water/air density. The proposed LBM was demonstrated to be valid and thermodynamically well-posed at high density ratios. However, thermodynamic convergence, especially at higher density ratios comes at a cost in terms of interface resolution requirements. For instance, at ![]() $T_r=0.36$ resulting in a density ratio of
$T_r=0.36$ resulting in a density ratio of ![]() $10^3$, to guarantee deviation below one percent from theory in the vapour phase, one must have
$10^3$, to guarantee deviation below one percent from theory in the vapour phase, one must have ![]() $W>8\delta r$. In large-scale hydrodynamic-dominated cases targeted in the present section, full thermodynamic convergence is not necessary. The only manifestations of deviation from the thermodynamically converged state that must be kept under control are spurious currents. Here, for density ratios
$W>8\delta r$. In large-scale hydrodynamic-dominated cases targeted in the present section, full thermodynamic convergence is not necessary. The only manifestations of deviation from the thermodynamically converged state that must be kept under control are spurious currents. Here, for density ratios ![]() $10^3$, the interface thickness, in (3.35), is fixed at
$10^3$, the interface thickness, in (3.35), is fixed at ![]() $W=5\delta r$ resulting in a seven percent deviation of the vapour phase density from theory and spurious currents below
$W=5\delta r$ resulting in a seven percent deviation of the vapour phase density from theory and spurious currents below ![]() $10^{-3}\delta r/\delta t$. The Tolman length for this choice of parameter is
$10^{-3}\delta r/\delta t$. The Tolman length for this choice of parameter is ![]() $\delta _T/\delta r=2.4$ which, for the resolutions considered below (
$\delta _T/\delta r=2.4$ which, for the resolutions considered below (![]() $R_0=75\delta r$), results in
$R_0=75\delta r$), results in ![]() $\delta _T/R_0=0.032$ therefore minimizing the impact of curvature on effective surface tension. Below, we consider benchmark simulations of dynamic effects at realistic density ratios of increasing complexity to probe the accuracy and numerical stability of our model in the dynamic setting.
$\delta _T/R_0=0.032$ therefore minimizing the impact of curvature on effective surface tension. Below, we consider benchmark simulations of dynamic effects at realistic density ratios of increasing complexity to probe the accuracy and numerical stability of our model in the dynamic setting.
5.2. Contact time on flat non-wetting surfaces
Extensive studies of drop impact dynamics have shown that the contact time on so-called super-hydrophobic surfaces is independent of the Weber number, ![]() $We=\rho _l D_0 U_0^2/\sigma$, and only scales with the inertio-capillary time,
$We=\rho _l D_0 U_0^2/\sigma$, and only scales with the inertio-capillary time, ![]() $\tau _i=\sqrt {\rho _l D_0^3/8\sigma }$, i.e. for a given drop initial diameter
$\tau _i=\sqrt {\rho _l D_0^3/8\sigma }$, i.e. for a given drop initial diameter ![]() $D_0$, the contact time is not affected by the impact velocity (Gauthier et al. Reference Gauthier, Symon, Clanet and Quéré2015). The different stages of the impact process are illustrated in figure 21 through water drops impacting two surfaces with different contact angles. Simulations carried out under the same conditions are shown and already point to very good agreement between simulations and experiments. To quantify the ability of the proposed model to capture the dynamics of drop impact and to investigate the Weber independence of the contact time on non-wetting surfaces, simulations were performed for a wide range of Weber numbers
$D_0$, the contact time is not affected by the impact velocity (Gauthier et al. Reference Gauthier, Symon, Clanet and Quéré2015). The different stages of the impact process are illustrated in figure 21 through water drops impacting two surfaces with different contact angles. Simulations carried out under the same conditions are shown and already point to very good agreement between simulations and experiments. To quantify the ability of the proposed model to capture the dynamics of drop impact and to investigate the Weber independence of the contact time on non-wetting surfaces, simulations were performed for a wide range of Weber numbers ![]() $\textit{We}\ \in [1,40]$, resulting in Reynolds numbers in the range of
$\textit{We}\ \in [1,40]$, resulting in Reynolds numbers in the range of ![]() $\textit{Re}\ \in [400, 1400]$, with
$\textit{Re}\ \in [400, 1400]$, with ![]() $\textit{Re}=U_0 D_0/\nu _l$. Simulations have been performed in boxes of size
$\textit{Re}=U_0 D_0/\nu _l$. Simulations have been performed in boxes of size ![]() $4D_0\times 4D_0\times 4D_0$ with
$4D_0\times 4D_0\times 4D_0$ with ![]() $D_0=150\delta r$. The temperature was set to
$D_0=150\delta r$. The temperature was set to ![]() $T_r=0.36$ resulting in a density ratio of
$T_r=0.36$ resulting in a density ratio of ![]() $10^3$. The obtained data show very good agreement with experimental contact times measured by Gauthier et al. (Reference Gauthier, Symon, Clanet and Quéré2015) and confirm the Weber independence of the contact times. Both numerical and experimental data are shown in figure 22.
$10^3$. The obtained data show very good agreement with experimental contact times measured by Gauthier et al. (Reference Gauthier, Symon, Clanet and Quéré2015) and confirm the Weber independence of the contact times. Both numerical and experimental data are shown in figure 22.

Figure 21. Drop impacting flat solid surface with different contact angles (first and second row) ![]() $\theta =180$ and (third and fourth row)
$\theta =180$ and (third and fourth row) ![]() $\theta =90$. The Weber and Reynolds number are respectively 3.5 and 750. Experimental data from Vadillo et al. (Reference Vadillo, Soucemarianadin, Delattre and Roux2009) are shown in the first and third rows. Density ratios in both experiments and simulations are
$\theta =90$. The Weber and Reynolds number are respectively 3.5 and 750. Experimental data from Vadillo et al. (Reference Vadillo, Soucemarianadin, Delattre and Roux2009) are shown in the first and third rows. Density ratios in both experiments and simulations are ![]() $10^3$ and kinematic viscosity ratios are set to 15.
$10^3$ and kinematic viscosity ratios are set to 15.

Figure 22. Drop contact times on flat non-wetting surface (contact angle ![]() $\theta =165$ for different Weber numbers as obtained from simulations and experiments. Simulations results are shown with red circular markers while experimental data reported by Gauthier et al. (Reference Gauthier, Symon, Clanet and Quéré2015) are illustrated with blue square markers. The dashed grey line represents the average contact time as obtained from simulations,
$\theta =165$ for different Weber numbers as obtained from simulations and experiments. Simulations results are shown with red circular markers while experimental data reported by Gauthier et al. (Reference Gauthier, Symon, Clanet and Quéré2015) are illustrated with blue square markers. The dashed grey line represents the average contact time as obtained from simulations, ![]() ${\bar {t_c}}/\tau _i=2.4$.
${\bar {t_c}}/\tau _i=2.4$.
5.3. Reducing the contact time: pancake bouncing
To further reduce the drop contact times, a number of different strategies have been devised during the past decades. Recently, Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) proposed to use macroscopic structures, in the form of tapered posts, to reduce the contact time. It has been shown that above a certain threshold Weber number, these structures can decrease the contact time by approximately ![]() $75$ %. This mechanism is also known as pancake bouncing, due to the pancake-like shape of the drop at take off. A detailed numerical study of pancake bouncing using LBM has been presented in (Mazloomi Moqaddam, Chikatamarla & Karlin Reference Mazloomi Moqaddam, Chikatamarla and Karlin2017) for a limited range of densities. Here, to further demonstrate the versatility of our model, we consider a realistic density ratio of
$75$ %. This mechanism is also known as pancake bouncing, due to the pancake-like shape of the drop at take off. A detailed numerical study of pancake bouncing using LBM has been presented in (Mazloomi Moqaddam, Chikatamarla & Karlin Reference Mazloomi Moqaddam, Chikatamarla and Karlin2017) for a limited range of densities. Here, to further demonstrate the versatility of our model, we consider a realistic density ratio of ![]() $10^3$. The geometry consists of a flat substrate populated by tapered posts of base and tip radii
$10^3$. The geometry consists of a flat substrate populated by tapered posts of base and tip radii ![]() $R_B$ and
$R_B$ and ![]() $R_b$ and height
$R_b$ and height ![]() $h$ with a centre-to-centre distance
$h$ with a centre-to-centre distance ![]() $w$ in a simple square arrangement. The simulations were run following the geometrical configurations considered in experiments (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014). Curved wall boundaries were implemented via the modified bounce-back scheme introduced by Bouzidi et al. (Reference Bouzidi, Firdaouss and Lallemand2001). The geometry is illustrated in figure 23. As for the flat substrate simulations, the domain size was set to
$w$ in a simple square arrangement. The simulations were run following the geometrical configurations considered in experiments (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014). Curved wall boundaries were implemented via the modified bounce-back scheme introduced by Bouzidi et al. (Reference Bouzidi, Firdaouss and Lallemand2001). The geometry is illustrated in figure 23. As for the flat substrate simulations, the domain size was set to ![]() $4D_0\times 4D_0\times 4D_0$ with
$4D_0\times 4D_0\times 4D_0$ with ![]() $D_0=150\delta r$. Snapshots from the different stages of impact for two different Weber numbers, one below the pancake bouncing threshold and one above, from both simulations and experiments are shown in figure 24. The results show excellent agreement between simulations and experiments. The contact times for different Weber numbers, as obtained from simulations, are compared to the experimental results from Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) in figure 25. It is shown that the numerical simulations not only accurately capture the contact time reduction due to pancake bouncing and the shape of the drop at take off, but they also correctly predict the onset of pancake bouncing. The shape of the drop at take off is assessed via the pancake quality parameter
$D_0=150\delta r$. Snapshots from the different stages of impact for two different Weber numbers, one below the pancake bouncing threshold and one above, from both simulations and experiments are shown in figure 24. The results show excellent agreement between simulations and experiments. The contact times for different Weber numbers, as obtained from simulations, are compared to the experimental results from Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) in figure 25. It is shown that the numerical simulations not only accurately capture the contact time reduction due to pancake bouncing and the shape of the drop at take off, but they also correctly predict the onset of pancake bouncing. The shape of the drop at take off is assessed via the pancake quality parameter ![]() $Q$ defined as the ratio of the drop radius at take off to its radius at maximum spreading (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014).
$Q$ defined as the ratio of the drop radius at take off to its radius at maximum spreading (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014).

Figure 23. Illustration of the geometry of tapered posts. Configuration follows the experiment setup by Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014).

Figure 24. Drop impacting tapered posts at different Weber numbers (first and second rows) ![]() $We=28.2$ with pancake bouncing and (third and fourth rows)
$We=28.2$ with pancake bouncing and (third and fourth rows) ![]() $We=14.2$. The first and third rows are experiments from Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) while the second and fourth rows are from simulations.
$We=14.2$. The first and third rows are experiments from Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) while the second and fourth rows are from simulations.

Figure 25. (a) Drop contact times and (b) pancake quality at rebound on tapered posts for different Weber numbers as obtained from simulations and experiments. Simulations results are shown with red circular markers while experimental data reported by Liu et al. (Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014) are illustrated with blue square markers.
5.4. Extreme density ratios: inertia-dominated coalescence of mercury drops
The sudden and pronounced topological changes involved in the coalescence of drops, especially the formation and subsequent evolution of the neck between them, have been of interest and subject to study for many years. The dynamics of the dimensionless neck radius ![]() $r_{neck}/R_0$ (with
$r_{neck}/R_0$ (with ![]() $R_0$ the drop's initial radius and
$R_0$ the drop's initial radius and ![]() $r_{neck}$ the neck radius) have been shown to belong to one of two regimes (Eggers, Lister & Stone Reference Eggers, Lister and Stone1999) characterized by the Ohnesorge number,
$r_{neck}$ the neck radius) have been shown to belong to one of two regimes (Eggers, Lister & Stone Reference Eggers, Lister and Stone1999) characterized by the Ohnesorge number, ![]() $Oh=\mu /\sqrt {2\rho _l\sigma R_0}$: highly viscous Stokes or inertial. The neck radius evolution over time has been shown to scale either as
$Oh=\mu /\sqrt {2\rho _l\sigma R_0}$: highly viscous Stokes or inertial. The neck radius evolution over time has been shown to scale either as ![]() $r_{neck}/R_0\propto t/\tau _i$ (in the viscous regime) or
$r_{neck}/R_0\propto t/\tau _i$ (in the viscous regime) or ![]() $r_{neck}/R_0\propto \sqrt {t/\tau _i}$ (in the inertial regime). Here, to better illustrate the ability of the proposed scheme to model flows with extreme density ratios, we will focus on the first regime, more specifically, the coalescence of mercury droplets, with Ohnesorge numbers of the order of
$r_{neck}/R_0\propto \sqrt {t/\tau _i}$ (in the inertial regime). Here, to better illustrate the ability of the proposed scheme to model flows with extreme density ratios, we will focus on the first regime, more specifically, the coalescence of mercury droplets, with Ohnesorge numbers of the order of ![]() $10^{-4}$ (for 1 g drops). We consider a case following the experimental configuration of Menchaca-Rocha et al. (Reference Menchaca-Rocha, Martínez-Dávalos, Núñez, Popinet and Zaleski2001) with two 1 g mercury droplets. To match the proper density ratio of a mercury/air system (
$10^{-4}$ (for 1 g drops). We consider a case following the experimental configuration of Menchaca-Rocha et al. (Reference Menchaca-Rocha, Martínez-Dávalos, Núñez, Popinet and Zaleski2001) with two 1 g mercury droplets. To match the proper density ratio of a mercury/air system (![]() $\rho _{Hg}=13\,600\ \text {kg}\ \text {m}^{-3}$), the temperature is set to
$\rho _{Hg}=13\,600\ \text {kg}\ \text {m}^{-3}$), the temperature is set to ![]() $T_r=0.267$, resulting in a density ratio of
$T_r=0.267$, resulting in a density ratio of ![]() $\rho _l/\rho _v\sim 11\,500$. The two drops, resolved with 150 points on their radii are placed in a rectangular domain of size
$\rho _l/\rho _v\sim 11\,500$. The two drops, resolved with 150 points on their radii are placed in a rectangular domain of size ![]() $400\times 400\times 800$ with a centre-to-centre distance of 304 points. The drops are connected initially via a neck of 4-points radius. The evolution of the drops’ shape over time are compared to experiments from Menchaca-Rocha et al. (Reference Menchaca-Rocha, Martínez-Dávalos, Núñez, Popinet and Zaleski2001) in figure 26. To further illustrate the agreement of numerical simulations with experiments, the evolution of the neck radii
$400\times 400\times 800$ with a centre-to-centre distance of 304 points. The drops are connected initially via a neck of 4-points radius. The evolution of the drops’ shape over time are compared to experiments from Menchaca-Rocha et al. (Reference Menchaca-Rocha, Martínez-Dávalos, Núñez, Popinet and Zaleski2001) in figure 26. To further illustrate the agreement of numerical simulations with experiments, the evolution of the neck radii ![]() $r_{neck}$ over time are shown in figure 27. Both qualitative comparison of the drops’ shape and quantitative comparison of the neck radius show that the presented solver is able to correctly model multi-phase flow dynamics with extreme density ratio. To the best of the authors’ knowledge, this is the first lattice Boltzmann simulation at such high density ratios, regardless of the formulation, i.e. pseudo-potential, free energy, phase-field etc.
$r_{neck}$ over time are shown in figure 27. Both qualitative comparison of the drops’ shape and quantitative comparison of the neck radius show that the presented solver is able to correctly model multi-phase flow dynamics with extreme density ratio. To the best of the authors’ knowledge, this is the first lattice Boltzmann simulation at such high density ratios, regardless of the formulation, i.e. pseudo-potential, free energy, phase-field etc.

Figure 26. Sequential images from different stages of the mercury drops coalescence and sub-sequential capillary waves propagation. First and third-row images are from experiments of Menchaca-Rocha et al. (Reference Menchaca-Rocha, Martínez-Dávalos, Núñez, Popinet and Zaleski2001), while second and fourth rows are from LB simulations. Snapshots are taken at ![]() $\Delta t=3.5$ ms intervals.
$\Delta t=3.5$ ms intervals.

Figure 27. Time evolution of the neck radii from both (grey line) simulations and (red circular markers) experiments as reported by Menchaca-Rocha et al. (Reference Menchaca-Rocha, Martínez-Dávalos, Núñez, Popinet and Zaleski2001). The dashed blue line represents the ![]() $\sqrt {t/\tau _i}$ scaling with
$\sqrt {t/\tau _i}$ scaling with ![]() $\tau _i=\sqrt {\rho R_0^3/\sigma }$.
$\tau _i=\sqrt {\rho R_0^3/\sigma }$.
6. Conclusion
Multi-phase flows are a well-established area in kinetic theory and more specifically in the context of the LBM. While dynamic two-dimensional/three-dimensional simulations are routinely carried out with the different LB-based formulations, which are subject to continuous numerical improvements, a clear and concise kinetic framework along with a characterisation of the resulting fluid thermodynamic properties is lacking.
The aim of the present work was to develop a general framework for isothermal single-component multi-phase flow simulations consistent with the capillary fluid thermodynamics. Starting from the first-order BBGKY equation and using a projector operator in phase-space, a flexible model, in terms of pressure contribution partition, is proposed. A specific realization of the partition minimizing deviations from the first-neighbour stencil reference (optimal) state was then discretized using the LBM. The discrete solver was shown to recover the full Navier–Stokes–Korteweg under the proposed scaling. The resulting discrete model was then probed for thermodynamic consistency and shown to abide by all the scaling laws of the corresponding meanfield, i.e. surface tension, interface thickness and Tolman length. Finally, the model was shown to allow for not only static, but dynamic large density ratios simulations with complex geometries, illustrated best by the extreme case of mercury drops coalescence, therefore effectively removing the well-known limitations on maximum density ratio.
The detailed study of the properties of the proposed model and accompanying theoretical analyses lead us to believe that the present framework fills important gaps in the multi-phase literature, more specifically in the context of discrete kinetic models such as the LBM. It provides a consistent framework for the simulation of challenging physics as demonstrated by the curvature dependence of the surface tension. Furthermore, it paves the way for extension to fully compressible non-ideal fluids and development of corresponding lattice Boltzmann solvers following our previously introduced compressible schemes (Saadat et al. Reference Saadat, Hosseini, Dorschner and Karlin2021) which will be the topic of an upcoming publication.
Acknowledgement
S.A.H. thanks M. Lulli for discussions on the Tolman length.
Funding
This work was supported by European Research Council (ERC) Advanced Grant no. 834763-PonD (S.A.H., B.D. and I.K.) and the Swiss National Science Foundation (SNSF) grant No. 200021-172640 (S.A.H.). Computational resources at the Swiss National Super Computing Center CSCS were provided under grant no. s1066.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Short-range interaction
The non-local contributions to particle's interaction in (2.15) consist of short- and long-range interactions, and are classically treated by splitting the integral over physical space into two domains, ![]() $\lvert \boldsymbol {r}_1-\boldsymbol {r}\lvert \,\leq\, d$ and
$\lvert \boldsymbol {r}_1-\boldsymbol {r}\lvert \,\leq\, d$ and ![]() $\lvert \boldsymbol {r}_1-\boldsymbol {r}\lvert\, >\, d$, where
$\lvert \boldsymbol {r}_1-\boldsymbol {r}\lvert\, >\, d$, where ![]() $d$ is the hard-sphere diameter. To derive the pressure form of the short-range interaction, we start with the Enskog hard-sphere collision integral (Enskog Reference Enskog1921; Chapman & Cowling Reference Chapman and Cowling1939),
$d$ is the hard-sphere diameter. To derive the pressure form of the short-range interaction, we start with the Enskog hard-sphere collision integral (Enskog Reference Enskog1921; Chapman & Cowling Reference Chapman and Cowling1939),
 \begin{align} \mathcal{J}_{E} &= d^2\iint \left[\chi\left(\boldsymbol{r}+\frac{d}{2}\boldsymbol{k}\right)f(\boldsymbol{r},\boldsymbol{v}') f(\boldsymbol{r}+{\rm d}\boldsymbol{k},\boldsymbol{v}_1')\right.\nonumber\\ &\quad \left. -\chi\left(\boldsymbol{r}-\frac{d}{2}\boldsymbol{k}\right)f(\boldsymbol{r},\boldsymbol{v}) f(\boldsymbol{r}-{\rm d}\boldsymbol{k},\boldsymbol{v}_1)\right] \boldsymbol{g}\boldsymbol{\cdot}\boldsymbol{k}\,{\rm d}\boldsymbol{k}\,{\rm d}\boldsymbol{v}_1, \end{align}
\begin{align} \mathcal{J}_{E} &= d^2\iint \left[\chi\left(\boldsymbol{r}+\frac{d}{2}\boldsymbol{k}\right)f(\boldsymbol{r},\boldsymbol{v}') f(\boldsymbol{r}+{\rm d}\boldsymbol{k},\boldsymbol{v}_1')\right.\nonumber\\ &\quad \left. -\chi\left(\boldsymbol{r}-\frac{d}{2}\boldsymbol{k}\right)f(\boldsymbol{r},\boldsymbol{v}) f(\boldsymbol{r}-{\rm d}\boldsymbol{k},\boldsymbol{v}_1)\right] \boldsymbol{g}\boldsymbol{\cdot}\boldsymbol{k}\,{\rm d}\boldsymbol{k}\,{\rm d}\boldsymbol{v}_1, \end{align}
where ![]() $\boldsymbol {k} = (\boldsymbol {r}_1-\boldsymbol {r})/\lvert \boldsymbol {r}_1-\boldsymbol {r}\lvert$,
$\boldsymbol {k} = (\boldsymbol {r}_1-\boldsymbol {r})/\lvert \boldsymbol {r}_1-\boldsymbol {r}\lvert$, ![]() $\boldsymbol {g}=\boldsymbol {v}_1-\boldsymbol {v}$,
$\boldsymbol {g}=\boldsymbol {v}_1-\boldsymbol {v}$, ![]() $\boldsymbol {v}'=\boldsymbol {v}+\boldsymbol {k}(\boldsymbol {g}\boldsymbol {\cdot }\boldsymbol {k})$,
$\boldsymbol {v}'=\boldsymbol {v}+\boldsymbol {k}(\boldsymbol {g}\boldsymbol {\cdot }\boldsymbol {k})$, ![]() $\boldsymbol {v}_1'=\boldsymbol {v}_1-\boldsymbol {k}(\boldsymbol {g}\boldsymbol {\cdot }\boldsymbol {k})$ and
$\boldsymbol {v}_1'=\boldsymbol {v}_1-\boldsymbol {k}(\boldsymbol {g}\boldsymbol {\cdot }\boldsymbol {k})$ and ![]() $\chi$ is the equilibrium pair correlation function, evaluated at local density taking into account the effect of volume of particles in the collision probability (Chapman & Cowling Reference Chapman and Cowling1939). Using a Taylor expansion around
$\chi$ is the equilibrium pair correlation function, evaluated at local density taking into account the effect of volume of particles in the collision probability (Chapman & Cowling Reference Chapman and Cowling1939). Using a Taylor expansion around ![]() $\boldsymbol {r}$,
$\boldsymbol {r}$,
and neglecting terms of order ![]() ${O}(d^4)$, the resulting approximation of the Enskog collision integral becomes
${O}(d^4)$, the resulting approximation of the Enskog collision integral becomes
where ![]() $\mathcal {J}$ is the Boltzmann collision integral for hard-spheres,
$\mathcal {J}$ is the Boltzmann collision integral for hard-spheres,
while ![]() $\mathcal {J}_{E}^{(1)}$ is the non-local contribution to the lowest order,
$\mathcal {J}_{E}^{(1)}$ is the non-local contribution to the lowest order,
 \begin{align} \mathcal{J}_{E}^{(1)} &= d^3 \chi(\boldsymbol{r}) \iint \boldsymbol{k}\boldsymbol{\cdot}[f(\boldsymbol{r},\boldsymbol{v}')\boldsymbol{\nabla} f(\boldsymbol{r},\boldsymbol{v}'_1)+ f(\boldsymbol{r},\boldsymbol{v})\boldsymbol{\nabla}f(\boldsymbol{r},\boldsymbol{v}_1) ] \boldsymbol{g}\boldsymbol{\cdot}\boldsymbol{k}\,{\rm d}\boldsymbol{k}\,{\rm d}\boldsymbol{v}_1 \nonumber\\ &\quad + \frac{d^3}{2} \iint \boldsymbol{k}\boldsymbol{\cdot}\boldsymbol{\nabla}\chi(\boldsymbol{r}) [f(\boldsymbol{r},\boldsymbol{v}')f(\boldsymbol{r},\boldsymbol{v}'_1) + f(\boldsymbol{r},\boldsymbol{v})f(\boldsymbol{r},\boldsymbol{v}_1)] \boldsymbol{g}\boldsymbol{\cdot}\boldsymbol{k}\,{\rm d}\boldsymbol{k}\,{\rm d}\boldsymbol{v}_1. \end{align}
\begin{align} \mathcal{J}_{E}^{(1)} &= d^3 \chi(\boldsymbol{r}) \iint \boldsymbol{k}\boldsymbol{\cdot}[f(\boldsymbol{r},\boldsymbol{v}')\boldsymbol{\nabla} f(\boldsymbol{r},\boldsymbol{v}'_1)+ f(\boldsymbol{r},\boldsymbol{v})\boldsymbol{\nabla}f(\boldsymbol{r},\boldsymbol{v}_1) ] \boldsymbol{g}\boldsymbol{\cdot}\boldsymbol{k}\,{\rm d}\boldsymbol{k}\,{\rm d}\boldsymbol{v}_1 \nonumber\\ &\quad + \frac{d^3}{2} \iint \boldsymbol{k}\boldsymbol{\cdot}\boldsymbol{\nabla}\chi(\boldsymbol{r}) [f(\boldsymbol{r},\boldsymbol{v}')f(\boldsymbol{r},\boldsymbol{v}'_1) + f(\boldsymbol{r},\boldsymbol{v})f(\boldsymbol{r},\boldsymbol{v}_1)] \boldsymbol{g}\boldsymbol{\cdot}\boldsymbol{k}\,{\rm d}\boldsymbol{k}\,{\rm d}\boldsymbol{v}_1. \end{align}Since the Boltzmann collision integral conserves the mass and momentum locally, it is annulled by the projector,
Furthermore, ![]() $\mathcal {J}_{SR}^{1}$ is evaluated at the local equilibrium
$\mathcal {J}_{SR}^{1}$ is evaluated at the local equilibrium ![]() $f^{eq}$ in (2.16) to get (Chapman & Cowling Reference Chapman and Cowling1939)
$f^{eq}$ in (2.16) to get (Chapman & Cowling Reference Chapman and Cowling1939)
which, after integration in ![]() $\boldsymbol {v}_1$ and
$\boldsymbol {v}_1$ and ![]() $\boldsymbol {k}$, for the isothermal flow, results in
$\boldsymbol {k}$, for the isothermal flow, results in
 \begin{align} \mathcal{J}_{E}^{(1)} &={-}b\rho\chi f^{eq}[(\boldsymbol{v}-\boldsymbol{u})\boldsymbol{\cdot}\boldsymbol{\nabla}\ln\rho^2\chi T] \nonumber\\ &\quad -b\rho\chi f^{eq}\left[\frac{2}{5RT}(\boldsymbol{v}-\boldsymbol{u})\otimes(\boldsymbol{v}-\boldsymbol{u}):\boldsymbol{\nabla}\boldsymbol{u} +\left(\frac{1}{5RT}{\lvert\boldsymbol{v}-\boldsymbol{u}\lvert}^2-1\right)\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u}\right], \end{align}
\begin{align} \mathcal{J}_{E}^{(1)} &={-}b\rho\chi f^{eq}[(\boldsymbol{v}-\boldsymbol{u})\boldsymbol{\cdot}\boldsymbol{\nabla}\ln\rho^2\chi T] \nonumber\\ &\quad -b\rho\chi f^{eq}\left[\frac{2}{5RT}(\boldsymbol{v}-\boldsymbol{u})\otimes(\boldsymbol{v}-\boldsymbol{u}):\boldsymbol{\nabla}\boldsymbol{u} +\left(\frac{1}{5RT}{\lvert\boldsymbol{v}-\boldsymbol{u}\lvert}^2-1\right)\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u}\right], \end{align}
where ![]() $b=2{\rm \pi} d^3/3m$. Finally, applying the isothermal projector
$b=2{\rm \pi} d^3/3m$. Finally, applying the isothermal projector ![]() $\mathcal {K}$, we obtain
$\mathcal {K}$, we obtain
 \begin{align} \mathcal{K}\mathcal{J}_{E}^{(1)} &=\frac{1}{\rho}\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\int\boldsymbol{v}\mathcal{J}^{(1)}_{E}\,{\rm d}\boldsymbol{v}\nonumber\\ &={-}\frac{1}{\rho}\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\int\boldsymbol{v}(\boldsymbol{v}-\boldsymbol{u}) f^{eq}(\boldsymbol{r},\boldsymbol{v})\,{\rm d}\boldsymbol{v}\boldsymbol{\cdot}\frac{b}{\rho T}\boldsymbol{\nabla}\rho^2\chi T\nonumber\\ &={-}\frac{1}{\rho}\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}b\rho^2\chi RT. \end{align}
\begin{align} \mathcal{K}\mathcal{J}_{E}^{(1)} &=\frac{1}{\rho}\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\int\boldsymbol{v}\mathcal{J}^{(1)}_{E}\,{\rm d}\boldsymbol{v}\nonumber\\ &={-}\frac{1}{\rho}\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\int\boldsymbol{v}(\boldsymbol{v}-\boldsymbol{u}) f^{eq}(\boldsymbol{r},\boldsymbol{v})\,{\rm d}\boldsymbol{v}\boldsymbol{\cdot}\frac{b}{\rho T}\boldsymbol{\nabla}\rho^2\chi T\nonumber\\ &={-}\frac{1}{\rho}\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}b\rho^2\chi RT. \end{align}While the phenomenological Enskog's collision integral (Enskog Reference Enskog1921) was used above, the lowest-order approximation in (A9) is identical in other versions of hard-sphere kinetic equations such as the revised Enskog theory (RET) (Van Beijeren & Ernst Reference Van Beijeren and Ernst1973) or kinetic variational theory (Karkheck & Stell Reference Karkheck and Stell1981).
Appendix B. Long-range interaction
Vlasov's mean-field approximation for a long-range interaction is reviewed next. Assuming the absence of correlations, the two-particle distribution function is approximated as
while the long-range interaction integral can be simplified to
 \begin{equation} \mathcal{J}_{V} = \frac{\partial f(\boldsymbol{r},\boldsymbol{v}) }{\partial\boldsymbol{v}}\boldsymbol{\cdot}\boldsymbol{\nabla}\left[\int_{\lvert\boldsymbol{r}_1-\boldsymbol{r}\lvert > d} \rho(\boldsymbol{r}_1)V(\lvert \boldsymbol{r}_1-\boldsymbol{r}\lvert) \,{\rm d}\boldsymbol{r}_1\right]. \end{equation}
\begin{equation} \mathcal{J}_{V} = \frac{\partial f(\boldsymbol{r},\boldsymbol{v}) }{\partial\boldsymbol{v}}\boldsymbol{\cdot}\boldsymbol{\nabla}\left[\int_{\lvert\boldsymbol{r}_1-\boldsymbol{r}\lvert > d} \rho(\boldsymbol{r}_1)V(\lvert \boldsymbol{r}_1-\boldsymbol{r}\lvert) \,{\rm d}\boldsymbol{r}_1\right]. \end{equation}
With a Taylor expansion around ![]() $\boldsymbol {r}$,
$\boldsymbol {r}$,
and neglecting higher-order terms, (B2) leads to
where parameters ![]() $a$ and
$a$ and ![]() $\kappa$ are, after integration over a unit sphere,
$\kappa$ are, after integration over a unit sphere,
Applying the projector, we obtain
 \begin{align} \mathcal{K}\mathcal{J}_{V} &=\frac{1}{\rho}\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\int\boldsymbol{v}\mathcal{J}_{V}\,{\rm d}\boldsymbol{v}\nonumber\\ &={-}\frac{1}{\rho}\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\int\boldsymbol{v} \frac{\partial}{\partial\boldsymbol{v}}f(\boldsymbol{r},\boldsymbol{v},t)\,{\rm d}\boldsymbol{v}\boldsymbol{\cdot}\boldsymbol{\nabla}[2 a \rho +\kappa \boldsymbol{\nabla}^2 \rho]\nonumber\\ &=\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}[2 a \rho +\kappa \boldsymbol{\nabla}^2 \rho]. \end{align}
\begin{align} \mathcal{K}\mathcal{J}_{V} &=\frac{1}{\rho}\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\int\boldsymbol{v}\mathcal{J}_{V}\,{\rm d}\boldsymbol{v}\nonumber\\ &={-}\frac{1}{\rho}\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\int\boldsymbol{v} \frac{\partial}{\partial\boldsymbol{v}}f(\boldsymbol{r},\boldsymbol{v},t)\,{\rm d}\boldsymbol{v}\boldsymbol{\cdot}\boldsymbol{\nabla}[2 a \rho +\kappa \boldsymbol{\nabla}^2 \rho]\nonumber\\ &=\frac{\partial f^{eq}}{\partial\boldsymbol{u}}\boldsymbol{\cdot}\boldsymbol{\nabla}[2 a \rho +\kappa \boldsymbol{\nabla}^2 \rho]. \end{align}
Finally, we can estimate the relative magnitude of the parameters ![]() $a$ and
$a$ and ![]() $\kappa$ by introducing a range of the attraction potential
$\kappa$ by introducing a range of the attraction potential ![]() $\delta$. Assuming
$\delta$. Assuming ![]() $d\ll \delta$, we have
$d\ll \delta$, we have ![]() $a\sim \bar {V}\delta ^3$ and
$a\sim \bar {V}\delta ^3$ and ![]() $\kappa \sim \bar {V}\delta ^5$, where
$\kappa \sim \bar {V}\delta ^5$, where ![]() $\bar {V}$ is a characteristic value of the potential, and thus
$\bar {V}$ is a characteristic value of the potential, and thus
Appendix C. Hydrodynamic limit of the Enskog–Vlasov–BGK kinetic model
C.1. Rescaled kinetic equation
For the Enskog–Vlasov–BGK kinetic model,
let us introduce the following parameters: characteristic flow velocity ![]() $\mathcal {U}$; characteristic flow scale
$\mathcal {U}$; characteristic flow scale ![]() $\mathcal {L}$; characteristic flow time
$\mathcal {L}$; characteristic flow time ![]() $\mathcal {T}=\mathcal {L}/\mathcal {U}$; characteristic density
$\mathcal {T}=\mathcal {L}/\mathcal {U}$; characteristic density ![]() $\bar {\rho }$; isothermal speed of sound of ideal gas
$\bar {\rho }$; isothermal speed of sound of ideal gas ![]() $c_s=\sqrt {RT}$; kinematic viscosity of the BGK model of ideal gas
$c_s=\sqrt {RT}$; kinematic viscosity of the BGK model of ideal gas ![]() $\nu =\tau c_s^2$. With the above, the variables are reduced as follows (primes denote non-dimensional variables): time
$\nu =\tau c_s^2$. With the above, the variables are reduced as follows (primes denote non-dimensional variables): time ![]() $t=\mathcal {T}t'$; space
$t=\mathcal {T}t'$; space ![]() $\boldsymbol {r}=\mathcal {L}\boldsymbol {r}'$; flow velocity
$\boldsymbol {r}=\mathcal {L}\boldsymbol {r}'$; flow velocity ![]() $\boldsymbol {u}=\mathcal {U}\boldsymbol {u}'$; particle velocity
$\boldsymbol {u}=\mathcal {U}\boldsymbol {u}'$; particle velocity ![]() $\boldsymbol {v}=c_s\boldsymbol {v}'$; density
$\boldsymbol {v}=c_s\boldsymbol {v}'$; density ![]() $\rho =\bar {\rho }\rho '$; distribution function
$\rho =\bar {\rho }\rho '$; distribution function ![]() $f=\bar {\rho }c_s^{-3}f'$. Furthermore, the following non-dimensional groups are introduced: viscosity-based Knudsen number
$f=\bar {\rho }c_s^{-3}f'$. Furthermore, the following non-dimensional groups are introduced: viscosity-based Knudsen number ![]() $Kn={\tau c_s}/{\mathcal {L}}$; Mach number
$Kn={\tau c_s}/{\mathcal {L}}$; Mach number ![]() $Ma={\mathcal {U}}/{c_s}$; Enskog number
$Ma={\mathcal {U}}/{c_s}$; Enskog number ![]() $En= b\bar {\rho }{Kn}/{Ma}$; Vlasov number
$En= b\bar {\rho }{Kn}/{Ma}$; Vlasov number ![]() $Vs={a}/{bRT}$. With this, the Enskog–Vlasov–BGK kinetic model is rescaled as follows:
$Vs={a}/{bRT}$. With this, the Enskog–Vlasov–BGK kinetic model is rescaled as follows:
 \begin{align} &Ma\,Kn\,\partial_{t}' f' + \boldsymbol{v}'\boldsymbol{\cdot} Kn\boldsymbol{\nabla}' f' ={-}(f' - {f^{eq}}')\nonumber\\ &\quad - \frac{1}{\rho'}\frac{\partial {f^{eq}}'}{\partial \boldsymbol{u}'}\boldsymbol{\cdot}{En} \left[\boldsymbol{\nabla}'(\chi (\rho')^2-Vs(\rho')^2){-\left(\frac{\delta}{\mathcal{L}}\right)^2\,Vs (\rho'\boldsymbol{\nabla}'\boldsymbol{\nabla}^{'2}\rho')}\right], \end{align}
\begin{align} &Ma\,Kn\,\partial_{t}' f' + \boldsymbol{v}'\boldsymbol{\cdot} Kn\boldsymbol{\nabla}' f' ={-}(f' - {f^{eq}}')\nonumber\\ &\quad - \frac{1}{\rho'}\frac{\partial {f^{eq}}'}{\partial \boldsymbol{u}'}\boldsymbol{\cdot}{En} \left[\boldsymbol{\nabla}'(\chi (\rho')^2-Vs(\rho')^2){-\left(\frac{\delta}{\mathcal{L}}\right)^2\,Vs (\rho'\boldsymbol{\nabla}'\boldsymbol{\nabla}^{'2}\rho')}\right], \end{align}
where ![]() $\delta$ is the range of the attraction potential, estimated according to (B8). The following scaling assumptions are applied: acoustic scaling,
$\delta$ is the range of the attraction potential, estimated according to (B8). The following scaling assumptions are applied: acoustic scaling, ![]() $Ma\sim 1$; hydrodynamic scaling,
$Ma\sim 1$; hydrodynamic scaling, ![]() $Kn\sim En\sim \delta /\mathcal {L}\sim \epsilon$; Enskog–Vlasov parity,
$Kn\sim En\sim \delta /\mathcal {L}\sim \epsilon$; Enskog–Vlasov parity, ![]() $Vs\sim 1$. In other words, the conventional hydrodynamic limit treats all non-dimensional groups that are inversely proportional to the flow scale
$Vs\sim 1$. In other words, the conventional hydrodynamic limit treats all non-dimensional groups that are inversely proportional to the flow scale ![]() $\mathcal {L}$ (
$\mathcal {L}$ (![]() $Kn$,
$Kn$, ![]() $En$ and
$En$ and ![]() $\delta /\mathcal {L}$) as a small parameter, while the Enskog–Vlasov parity ensures that both the short- and long-range contributions to the pressure are treated on equal footing. Returning to dimensional variables, we may write
$\delta /\mathcal {L}$) as a small parameter, while the Enskog–Vlasov parity ensures that both the short- and long-range contributions to the pressure are treated on equal footing. Returning to dimensional variables, we may write
where
Finally, taking into account the reference equilibrium in (2.34) and the reference pressure ![]() $P_0$, the rescaled kinetic equation in (2.35) takes the form of (C3) with
$P_0$, the rescaled kinetic equation in (2.35) takes the form of (C3) with
Chapman–Enskog analysis of the rescaled kinetic equation in (2.35) is presented in the next section.
C.2. Chapman–Enskog analysis
Expanding the distribution function as
introducing it back into (C3) and separating terms with different orders in ![]() $\epsilon$, at order zero, one recovers
$\epsilon$, at order zero, one recovers
This latter implies the solvability conditions,
At order ![]() $\epsilon$:
$\epsilon$:
which, upon integration in ![]() $\boldsymbol {v}$, leads to
$\boldsymbol {v}$, leads to
At order ![]() $\epsilon ^2$:
$\epsilon ^2$:
which leads to the following equation for mass conservation:
while for momentum:
The last term on the left-hand side can be evaluated using the previous order in ![]() $\epsilon$ as
$\epsilon$ as
 \begin{align} \int \boldsymbol{v}\otimes\boldsymbol{v} f^{(1)}\,{\rm d}\boldsymbol{v} &={-}\tau\left[\partial_t^{(1)}\int \boldsymbol{v}\otimes\boldsymbol{v} f^{(0)}\,{\rm d}\boldsymbol{v} + \boldsymbol{\nabla}\boldsymbol{\cdot}\int \boldsymbol{v}\otimes\boldsymbol{v}\otimes\boldsymbol{v} f^{(0)}\,{\rm d}\boldsymbol{v} \right. \nonumber\\ &\quad \left. +\frac{1}{\rho} \int \boldsymbol{v}\otimes\boldsymbol{v} \frac{\partial f^{eq}}{\partial \boldsymbol{u}}\boldsymbol{\cdot}\boldsymbol{F}^{(1)} d\boldsymbol{v}\right], \end{align}
\begin{align} \int \boldsymbol{v}\otimes\boldsymbol{v} f^{(1)}\,{\rm d}\boldsymbol{v} &={-}\tau\left[\partial_t^{(1)}\int \boldsymbol{v}\otimes\boldsymbol{v} f^{(0)}\,{\rm d}\boldsymbol{v} + \boldsymbol{\nabla}\boldsymbol{\cdot}\int \boldsymbol{v}\otimes\boldsymbol{v}\otimes\boldsymbol{v} f^{(0)}\,{\rm d}\boldsymbol{v} \right. \nonumber\\ &\quad \left. +\frac{1}{\rho} \int \boldsymbol{v}\otimes\boldsymbol{v} \frac{\partial f^{eq}}{\partial \boldsymbol{u}}\boldsymbol{\cdot}\boldsymbol{F}^{(1)} d\boldsymbol{v}\right], \end{align}where
 \begin{align} \partial_t^{(1)}\int \boldsymbol{v}\otimes\boldsymbol{v} f^{(0)}\,{\rm d}\boldsymbol{v} &={-}\boldsymbol{\nabla}\boldsymbol{\cdot} \rho \boldsymbol{u}\otimes\boldsymbol{u}\otimes\boldsymbol{u} - [\boldsymbol{u}\otimes(\boldsymbol{F}^{(1)}+\boldsymbol{\nabla}P_0) + (\boldsymbol{F}^{(1)}\nonumber\\ &\quad +\boldsymbol{\nabla}P_0)\otimes\boldsymbol{u}] + \partial_t^{(1)} P_0\boldsymbol{\mathsf{I}}, \end{align}
\begin{align} \partial_t^{(1)}\int \boldsymbol{v}\otimes\boldsymbol{v} f^{(0)}\,{\rm d}\boldsymbol{v} &={-}\boldsymbol{\nabla}\boldsymbol{\cdot} \rho \boldsymbol{u}\otimes\boldsymbol{u}\otimes\boldsymbol{u} - [\boldsymbol{u}\otimes(\boldsymbol{F}^{(1)}+\boldsymbol{\nabla}P_0) + (\boldsymbol{F}^{(1)}\nonumber\\ &\quad +\boldsymbol{\nabla}P_0)\otimes\boldsymbol{u}] + \partial_t^{(1)} P_0\boldsymbol{\mathsf{I}}, \end{align}and
which leads to
where the last two terms can be re-written as
 \begin{align} \partial_t^{(1)}P_0 + \boldsymbol{\nabla}\boldsymbol{\cdot} P_0 \boldsymbol{u} &= \frac{\partial P_0}{\partial \rho}(\partial_t^{(1)}\rho + \boldsymbol{\nabla}\boldsymbol{\cdot}\rho \boldsymbol{u}) + \left(P_0 -\rho\frac{\partial P_0}{\partial \rho}\right)\boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{u}\nonumber\\ &= P_0\left(1 - \frac{\partial \ln P_0}{\partial \ln \rho}\right)\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u}, \end{align}
\begin{align} \partial_t^{(1)}P_0 + \boldsymbol{\nabla}\boldsymbol{\cdot} P_0 \boldsymbol{u} &= \frac{\partial P_0}{\partial \rho}(\partial_t^{(1)}\rho + \boldsymbol{\nabla}\boldsymbol{\cdot}\rho \boldsymbol{u}) + \left(P_0 -\rho\frac{\partial P_0}{\partial \rho}\right)\boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{u}\nonumber\\ &= P_0\left(1 - \frac{\partial \ln P_0}{\partial \ln \rho}\right)\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u}, \end{align}in turn recovering the Navier–Stokes-level momentum equation:
where
Appendix D. Chapman–Enskog analysis of the lattice Boltzmann model
Using a Taylor expansion around ![]() $(\boldsymbol {r},t)$,
$(\boldsymbol {r},t)$,
the discrete time-evolution equation is re-written as
where we have only retained terms up to order two. Then, introducing characteristic flow size ![]() $\mathcal {L}$ and velocity
$\mathcal {L}$ and velocity ![]() $\mathcal {U}$, the equation is made non-dimensional as
$\mathcal {U}$, the equation is made non-dimensional as
where primed variables denote non-dimensional form and
where ![]() $c=\delta r/\delta t$. Assuming acoustic, i.e.
$c=\delta r/\delta t$. Assuming acoustic, i.e. ![]() ${\mathcal {U}}/{c}\sim 1$, and hydrodynamic, i.e.
${\mathcal {U}}/{c}\sim 1$, and hydrodynamic, i.e. ![]() ${\delta r}/{\mathcal {L}}\sim {\delta u}/{\mathcal {U}}\sim \varepsilon$, scaling and dropping the primes for the sake of readability,
${\delta r}/{\mathcal {L}}\sim {\delta u}/{\mathcal {U}}\sim \varepsilon$, scaling and dropping the primes for the sake of readability,
Then introducing multi-scale expansions,
the following equations are recovered at scales ![]() $\varepsilon$ and
$\varepsilon$ and ![]() $\varepsilon ^2$:
$\varepsilon ^2$:
with ![]() $f_i^{(0)}={f_i^*}^{(0)}=f_i^{eq}$. The moments of the non-local contributions (including both non-ideal contributions to the thermodynamic pressure, surface tension and the correction for the diagonals of the third-order moments tensor) are
$f_i^{(0)}={f_i^*}^{(0)}=f_i^{eq}$. The moments of the non-local contributions (including both non-ideal contributions to the thermodynamic pressure, surface tension and the correction for the diagonals of the third-order moments tensor) are
Taking the moments of the Chapman–Enskog-expanded equation at order ![]() $\varepsilon$,
$\varepsilon$,
while at order ![]() $\varepsilon ^2$, the continuity equation is
$\varepsilon ^2$, the continuity equation is
Summing up (D10) and (D12), we recover the continuity equation as
where ![]() $\boldsymbol {U} = \boldsymbol {u} + ({\delta t}/{2\rho })\boldsymbol {F}$. For the momentum equations, we have
$\boldsymbol {U} = \boldsymbol {u} + ({\delta t}/{2\rho })\boldsymbol {F}$. For the momentum equations, we have
 \begin{align} &\partial_t^{(2)}\rho \boldsymbol{u} + \frac{1}{2} \partial_t^{(1)} \boldsymbol{F} + \frac{1}{2}\boldsymbol{\nabla}\boldsymbol{\cdot}(\boldsymbol{u}\otimes\boldsymbol{F} + {\boldsymbol{F}\otimes\boldsymbol{u}} )+ \boldsymbol{\nabla}\boldsymbol{\cdot}\left(\frac{1}{2}-\frac{1}{\omega}\right) [\partial_t^{(1)}{\boldsymbol{\mathsf{\Phi}}}_{2}^{(0)}+\boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{\mathsf{\Phi}}}_{3}^{(0)}]\nonumber\\ &\quad - \boldsymbol{\nabla}\boldsymbol{\cdot}\left(\frac{1}{2}-\frac{1}{\omega}\right) (\boldsymbol{u}\otimes\boldsymbol{F} + {\boldsymbol{F}\otimes\boldsymbol{u}}) + \boldsymbol{\nabla}\boldsymbol{\cdot}\frac{1}{\omega}{\boldsymbol{\mathsf{\Phi}}} = 0, \end{align}
\begin{align} &\partial_t^{(2)}\rho \boldsymbol{u} + \frac{1}{2} \partial_t^{(1)} \boldsymbol{F} + \frac{1}{2}\boldsymbol{\nabla}\boldsymbol{\cdot}(\boldsymbol{u}\otimes\boldsymbol{F} + {\boldsymbol{F}\otimes\boldsymbol{u}} )+ \boldsymbol{\nabla}\boldsymbol{\cdot}\left(\frac{1}{2}-\frac{1}{\omega}\right) [\partial_t^{(1)}{\boldsymbol{\mathsf{\Phi}}}_{2}^{(0)}+\boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{\mathsf{\Phi}}}_{3}^{(0)}]\nonumber\\ &\quad - \boldsymbol{\nabla}\boldsymbol{\cdot}\left(\frac{1}{2}-\frac{1}{\omega}\right) (\boldsymbol{u}\otimes\boldsymbol{F} + {\boldsymbol{F}\otimes\boldsymbol{u}}) + \boldsymbol{\nabla}\boldsymbol{\cdot}\frac{1}{\omega}{\boldsymbol{\mathsf{\Phi}}} = 0, \end{align}
where ![]() ${\boldsymbol{\mathsf{\Phi}}} _{2}^{(0)}$ and
${\boldsymbol{\mathsf{\Phi}}} _{2}^{(0)}$ and ![]() ${\boldsymbol{\mathsf{\Phi}}} _{3}^{(0)}$ are the second- and third-order moments of
${\boldsymbol{\mathsf{\Phi}}} _{3}^{(0)}$ are the second- and third-order moments of ![]() $f_i^{(0)}$ defined as
$f_i^{(0)}$ defined as
where ![]() ${\boldsymbol{\mathsf{\Phi}}} _{\alpha \beta \gamma }^{MB}=\rho u_\alpha u_\beta u_\gamma + P_0\,{\rm perm}(u_\alpha \delta _{\beta \gamma })$ is the third-order moment of the Maxwell–Boltzmann distribution, and for the sake of simplicity, we have introduced the diagonal rank three tensor
${\boldsymbol{\mathsf{\Phi}}} _{\alpha \beta \gamma }^{MB}=\rho u_\alpha u_\beta u_\gamma + P_0\,{\rm perm}(u_\alpha \delta _{\beta \gamma })$ is the third-order moment of the Maxwell–Boltzmann distribution, and for the sake of simplicity, we have introduced the diagonal rank three tensor ![]() $\boldsymbol {J}$, with
$\boldsymbol {J}$, with ![]() $J_{\alpha \beta \gamma }=\delta _{\alpha \beta }\delta _{\alpha \gamma }\delta _{\beta \gamma }$ and
$J_{\alpha \beta \gamma }=\delta _{\alpha \beta }\delta _{\alpha \gamma }\delta _{\beta \gamma }$ and ![]() $\circ$ is the Hadamard product. The contributions in the fourth term on the left-hand side can be expanded as
$\circ$ is the Hadamard product. The contributions in the fourth term on the left-hand side can be expanded as
 \begin{align} \partial_t^{(1)} {\boldsymbol{\mathsf{\Phi}}}_{2}^{(0)}&= \partial_t^{(1)}\rho \boldsymbol{u}\otimes\boldsymbol{u} + \partial_t^{(1)} P_0\boldsymbol{\mathsf{I}}\nonumber\\ &=\boldsymbol{u}\otimes\partial_t^{(1)}\rho \boldsymbol{u} + {(\partial_t^{(1)}\rho \boldsymbol{u})\otimes\boldsymbol{u}} - \boldsymbol{u}\otimes\boldsymbol{u} \partial_t^{(1)} \rho + \partial_t^{(1)} P_0 \boldsymbol{\mathsf{I}}\nonumber\\ &={-}\boldsymbol{\nabla}\boldsymbol{\cdot}\rho \boldsymbol{u}\otimes\boldsymbol{u}\otimes\boldsymbol{u} -[\boldsymbol{u}\otimes(\boldsymbol{\nabla} P_0 - \boldsymbol{F}) + {(\boldsymbol{\nabla} P_0 - \boldsymbol{F})\otimes\boldsymbol{u}}] + \partial_t^{(1)}P_0 \boldsymbol{\mathsf{I}} \end{align}
\begin{align} \partial_t^{(1)} {\boldsymbol{\mathsf{\Phi}}}_{2}^{(0)}&= \partial_t^{(1)}\rho \boldsymbol{u}\otimes\boldsymbol{u} + \partial_t^{(1)} P_0\boldsymbol{\mathsf{I}}\nonumber\\ &=\boldsymbol{u}\otimes\partial_t^{(1)}\rho \boldsymbol{u} + {(\partial_t^{(1)}\rho \boldsymbol{u})\otimes\boldsymbol{u}} - \boldsymbol{u}\otimes\boldsymbol{u} \partial_t^{(1)} \rho + \partial_t^{(1)} P_0 \boldsymbol{\mathsf{I}}\nonumber\\ &={-}\boldsymbol{\nabla}\boldsymbol{\cdot}\rho \boldsymbol{u}\otimes\boldsymbol{u}\otimes\boldsymbol{u} -[\boldsymbol{u}\otimes(\boldsymbol{\nabla} P_0 - \boldsymbol{F}) + {(\boldsymbol{\nabla} P_0 - \boldsymbol{F})\otimes\boldsymbol{u}}] + \partial_t^{(1)}P_0 \boldsymbol{\mathsf{I}} \end{align}and
 \begin{align} \boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{\mathsf{\Phi}}}_{3}^{(0)} &= \boldsymbol{\nabla}\boldsymbol{\cdot}\rho \boldsymbol{u}\otimes\boldsymbol{u}\otimes\boldsymbol{u} + (\boldsymbol{\nabla} P_0 \boldsymbol{u} + {\boldsymbol{\nabla} P_0 \boldsymbol{u}}^{{{\dagger}}}) + (\boldsymbol{\nabla}\boldsymbol{\cdot}P_0\boldsymbol{u})\boldsymbol{\mathsf{I}}\nonumber\\ &\quad - \boldsymbol{\nabla}\boldsymbol{\cdot}[\rho\boldsymbol{u}\otimes \boldsymbol{u} \otimes\boldsymbol{u}\circ\boldsymbol{J} + 3\left(P_0 - \rho \varsigma^2\right) \boldsymbol{u}\otimes\boldsymbol{\mathsf{I}}\circ\boldsymbol{\mathsf{J}}], \end{align}
\begin{align} \boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{\mathsf{\Phi}}}_{3}^{(0)} &= \boldsymbol{\nabla}\boldsymbol{\cdot}\rho \boldsymbol{u}\otimes\boldsymbol{u}\otimes\boldsymbol{u} + (\boldsymbol{\nabla} P_0 \boldsymbol{u} + {\boldsymbol{\nabla} P_0 \boldsymbol{u}}^{{{\dagger}}}) + (\boldsymbol{\nabla}\boldsymbol{\cdot}P_0\boldsymbol{u})\boldsymbol{\mathsf{I}}\nonumber\\ &\quad - \boldsymbol{\nabla}\boldsymbol{\cdot}[\rho\boldsymbol{u}\otimes \boldsymbol{u} \otimes\boldsymbol{u}\circ\boldsymbol{J} + 3\left(P_0 - \rho \varsigma^2\right) \boldsymbol{u}\otimes\boldsymbol{\mathsf{I}}\circ\boldsymbol{\mathsf{J}}], \end{align}resulting in
 \begin{align} &\partial_t^{(1)} {\boldsymbol{\mathsf{\Phi}}}_{2}^{(0)} + \boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{\mathsf{\Phi}}}_{3}^{(0)} = P_0(\boldsymbol{\nabla}\boldsymbol{u} + {\boldsymbol{\nabla}\boldsymbol{u}}^{{{\dagger}}} ) + (\boldsymbol{u}\otimes\boldsymbol{F} + {\boldsymbol{u}\otimes\boldsymbol{F}}^{{{\dagger}}})\nonumber\\ &\quad + (\boldsymbol{\nabla}\boldsymbol{\cdot} P_0 \boldsymbol{u} + \partial_t^{(1)}P_0)\boldsymbol{\mathsf{I}} - \boldsymbol{\nabla}\boldsymbol{\cdot}[\rho\boldsymbol{u}\otimes \boldsymbol{u} \otimes\boldsymbol{u}\circ\boldsymbol{\mathsf{J}} + 3\left(P_0 - \rho \varsigma^2\right) \boldsymbol{u}\otimes\boldsymbol{\mathsf{I}}\circ\boldsymbol{J}]. \end{align}
\begin{align} &\partial_t^{(1)} {\boldsymbol{\mathsf{\Phi}}}_{2}^{(0)} + \boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{\mathsf{\Phi}}}_{3}^{(0)} = P_0(\boldsymbol{\nabla}\boldsymbol{u} + {\boldsymbol{\nabla}\boldsymbol{u}}^{{{\dagger}}} ) + (\boldsymbol{u}\otimes\boldsymbol{F} + {\boldsymbol{u}\otimes\boldsymbol{F}}^{{{\dagger}}})\nonumber\\ &\quad + (\boldsymbol{\nabla}\boldsymbol{\cdot} P_0 \boldsymbol{u} + \partial_t^{(1)}P_0)\boldsymbol{\mathsf{I}} - \boldsymbol{\nabla}\boldsymbol{\cdot}[\rho\boldsymbol{u}\otimes \boldsymbol{u} \otimes\boldsymbol{u}\circ\boldsymbol{\mathsf{J}} + 3\left(P_0 - \rho \varsigma^2\right) \boldsymbol{u}\otimes\boldsymbol{\mathsf{I}}\circ\boldsymbol{J}]. \end{align}Plugging this last equation back into (D14),
 \begin{align} &\partial_t^{(2)}\rho \boldsymbol{u} + \partial_t^{(1)}\frac{\boldsymbol{F}}{2} + \frac{1}{2}\boldsymbol{\nabla}\boldsymbol{\cdot}(\boldsymbol{u}\otimes\boldsymbol{F} + {\boldsymbol{F}\otimes\boldsymbol{u}}) + \boldsymbol{\nabla}\boldsymbol{\cdot}\left(\frac{1}{2}-\frac{1}{\omega}\right)P_0(\boldsymbol{\nabla}\boldsymbol{u} + {\boldsymbol{\nabla}\boldsymbol{u}}^{{{\dagger}}})\nonumber\\ &\quad + \boldsymbol{\nabla}\left(\frac{1}{2}-\frac{1}{\omega}\right) (\partial_t^{(1)}P_0+\boldsymbol{\nabla}\boldsymbol{\cdot} P_0 \boldsymbol{u}) \nonumber\\ &\quad +\boldsymbol{\nabla}\boldsymbol{\cdot}\left[\left(\frac{1}{2}-\frac{1}{\omega}\right) \boldsymbol{\nabla}\boldsymbol{\cdot}(\rho\boldsymbol{u}\otimes \boldsymbol{u} \otimes\boldsymbol{u}\circ\boldsymbol{\mathsf{J}} + 3\left(P_0 - \rho \varsigma^2\right) \boldsymbol{u}\otimes\boldsymbol{\mathsf{I}}\circ\boldsymbol{\mathsf{J}}) + \frac{1}{\omega}{\boldsymbol{\mathsf{\Phi}}}\right] = 0, \end{align}
\begin{align} &\partial_t^{(2)}\rho \boldsymbol{u} + \partial_t^{(1)}\frac{\boldsymbol{F}}{2} + \frac{1}{2}\boldsymbol{\nabla}\boldsymbol{\cdot}(\boldsymbol{u}\otimes\boldsymbol{F} + {\boldsymbol{F}\otimes\boldsymbol{u}}) + \boldsymbol{\nabla}\boldsymbol{\cdot}\left(\frac{1}{2}-\frac{1}{\omega}\right)P_0(\boldsymbol{\nabla}\boldsymbol{u} + {\boldsymbol{\nabla}\boldsymbol{u}}^{{{\dagger}}})\nonumber\\ &\quad + \boldsymbol{\nabla}\left(\frac{1}{2}-\frac{1}{\omega}\right) (\partial_t^{(1)}P_0+\boldsymbol{\nabla}\boldsymbol{\cdot} P_0 \boldsymbol{u}) \nonumber\\ &\quad +\boldsymbol{\nabla}\boldsymbol{\cdot}\left[\left(\frac{1}{2}-\frac{1}{\omega}\right) \boldsymbol{\nabla}\boldsymbol{\cdot}(\rho\boldsymbol{u}\otimes \boldsymbol{u} \otimes\boldsymbol{u}\circ\boldsymbol{\mathsf{J}} + 3\left(P_0 - \rho \varsigma^2\right) \boldsymbol{u}\otimes\boldsymbol{\mathsf{I}}\circ\boldsymbol{\mathsf{J}}) + \frac{1}{\omega}{\boldsymbol{\mathsf{\Phi}}}\right] = 0, \end{align}where the last term cancels out by setting
and the fourth and fifth terms reduce to the viscous stress tensor by defining ![]() $\mu /P_0 = ({1}/{\omega } - {1}/{2})$ and
$\mu /P_0 = ({1}/{\omega } - {1}/{2})$ and
Furthermore, using ![]() $\boldsymbol {U} = \boldsymbol {u} + ({\delta t}/{2\rho })\boldsymbol {F}$ and
$\boldsymbol {U} = \boldsymbol {u} + ({\delta t}/{2\rho })\boldsymbol {F}$ and
in combination with the Euler-level equation, and keeping in mind that errors of the form ![]() $\boldsymbol {\nabla }\boldsymbol {\cdot }{(\delta t^2\boldsymbol {F}\otimes \boldsymbol {F})}/{4\rho }$ in the convective term and
$\boldsymbol {\nabla }\boldsymbol {\cdot }{(\delta t^2\boldsymbol {F}\otimes \boldsymbol {F})}/{4\rho }$ in the convective term and ![]() $\delta t\boldsymbol {\nabla }\mu (\boldsymbol {\nabla }({\boldsymbol {F}}/{\rho }) +\boldsymbol {\nabla }({\boldsymbol {F}}/{\rho })^{{\dagger} })$ in the viscous stress are of order
$\delta t\boldsymbol {\nabla }\mu (\boldsymbol {\nabla }({\boldsymbol {F}}/{\rho }) +\boldsymbol {\nabla }({\boldsymbol {F}}/{\rho })^{{\dagger} })$ in the viscous stress are of order ![]() $\varepsilon ^3$, one recovers
$\varepsilon ^3$, one recovers
 \begin{align} &\partial_t\rho \boldsymbol{U} + \boldsymbol{\nabla}\boldsymbol{\cdot} \rho \boldsymbol{U}\otimes\boldsymbol{U} - \boldsymbol{\nabla}\boldsymbol{\cdot}\mu\left( \boldsymbol{\nabla}\boldsymbol{U} + {\boldsymbol{\nabla}\boldsymbol{U}}^{{{\dagger}}} - \frac{2}{D}\boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{U} \boldsymbol{\mathsf{I}}\right)\nonumber\\ &\quad - \boldsymbol{\nabla}\boldsymbol{\cdot} (\eta \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{U}) + {O}(\varepsilon^3) = 0. \end{align}
\begin{align} &\partial_t\rho \boldsymbol{U} + \boldsymbol{\nabla}\boldsymbol{\cdot} \rho \boldsymbol{U}\otimes\boldsymbol{U} - \boldsymbol{\nabla}\boldsymbol{\cdot}\mu\left( \boldsymbol{\nabla}\boldsymbol{U} + {\boldsymbol{\nabla}\boldsymbol{U}}^{{{\dagger}}} - \frac{2}{D}\boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{U} \boldsymbol{\mathsf{I}}\right)\nonumber\\ &\quad - \boldsymbol{\nabla}\boldsymbol{\cdot} (\eta \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{U}) + {O}(\varepsilon^3) = 0. \end{align}
The scaling parameter introduced for the perturbation analysis, and consistency at the first two orders in ![]() $\varepsilon$, is further confirmed by simulations. To demonstrate this point, flat interface simulations at
$\varepsilon$, is further confirmed by simulations. To demonstrate this point, flat interface simulations at ![]() $T_r=0.36$ have been conducted for different values of
$T_r=0.36$ have been conducted for different values of ![]() $\varepsilon$. The expansion parameter is controlled by introducing a scaling parameter
$\varepsilon$. The expansion parameter is controlled by introducing a scaling parameter ![]() $k$ into the pressure
$k$ into the pressure ![]() $P$ appearing inside the pseudo-potential,
$P$ appearing inside the pseudo-potential, ![]() $P'=kP$, the reference pressure
$P'=kP$, the reference pressure ![]() $P_0'=k P_0$ and the surface tension term resulting in
$P_0'=k P_0$ and the surface tension term resulting in ![]() $\boldsymbol {F}'=k\boldsymbol {F}$. As introduced here, the scaling parameter directly scales the magnitude of the force term and therefore
$\boldsymbol {F}'=k\boldsymbol {F}$. As introduced here, the scaling parameter directly scales the magnitude of the force term and therefore ![]() $k/\rho \sim \varepsilon$. It must be noted that this scaling is akin to a space grid refinement. The results obtained for different values of
$k/\rho \sim \varepsilon$. It must be noted that this scaling is akin to a space grid refinement. The results obtained for different values of ![]() $k$ are shown in figure 28 and point to a second-order scaling in agreement with the theoretical analysis provided in the manuscript.
$k$ are shown in figure 28 and point to a second-order scaling in agreement with the theoretical analysis provided in the manuscript.

Figure 28. Error in vapour-phase coexistence density, ![]() $E={\lvert \rho _{v,ref} - \rho _{v,sim}\lvert }/{\rho _{v,ref}}$, as obtained from flat interface simulations (red circular markers). The dashed line shows the slope 2.
$E={\lvert \rho _{v,ref} - \rho _{v,sim}\lvert }/{\rho _{v,ref}}$, as obtained from flat interface simulations (red circular markers). The dashed line shows the slope 2.
Appendix E. Discrete non-local contributions to pressure tensor
Following the analysis presented by Shan (Reference Shan2008), we write the force contribution for the present model as
 $$\begin{gather}\boldsymbol{F}^{A} ={\pm}\frac{8}{3} \psi(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_{i} \psi(\boldsymbol{r}+\boldsymbol{c}_i\delta t), \end{gather}$$
$$\begin{gather}\boldsymbol{F}^{A} ={\pm}\frac{8}{3} \psi(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_{i} \psi(\boldsymbol{r}+\boldsymbol{c}_i\delta t), \end{gather}$$ $$\begin{gather}\boldsymbol{F}^{B} ={\mp} \frac{1}{3} \psi(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\psi(\boldsymbol{r}+2\boldsymbol{c}_i\delta t), \end{gather}$$
$$\begin{gather}\boldsymbol{F}^{B} ={\mp} \frac{1}{3} \psi(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\psi(\boldsymbol{r}+2\boldsymbol{c}_i\delta t), \end{gather}$$ $$\begin{gather}\boldsymbol{F}^{C} = 2\tilde{\kappa} \rho(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\rho(\boldsymbol{r}+\boldsymbol{c}_i\delta t), \end{gather}$$
$$\begin{gather}\boldsymbol{F}^{C} = 2\tilde{\kappa} \rho(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\rho(\boldsymbol{r}+\boldsymbol{c}_i\delta t), \end{gather}$$ $$\begin{gather}\boldsymbol{F}^{D} ={-}\tilde{\kappa} \rho(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\rho(\boldsymbol{r}+2\boldsymbol{c}_i\delta t). \end{gather}$$
$$\begin{gather}\boldsymbol{F}^{D} ={-}\tilde{\kappa} \rho(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\rho(\boldsymbol{r}+2\boldsymbol{c}_i\delta t). \end{gather}$$
The pressure tensor contributions from forces ![]() $\boldsymbol {F}^{A}$ and
$\boldsymbol {F}^{A}$ and ![]() $\boldsymbol {F}^{C}$ can be readily written as
$\boldsymbol {F}^{C}$ can be readily written as
 $$\begin{gather} \boldsymbol{P}^{A} ={\mp}\frac{8}{6} \psi(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \psi(\boldsymbol{r}+\boldsymbol{c}_i\delta t), \end{gather}$$
$$\begin{gather} \boldsymbol{P}^{A} ={\mp}\frac{8}{6} \psi(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \psi(\boldsymbol{r}+\boldsymbol{c}_i\delta t), \end{gather}$$ $$\begin{gather}\boldsymbol{P}^{C} ={-}\tilde{\kappa} \rho(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \rho(\boldsymbol{r}+\boldsymbol{c}_i\delta t), \end{gather}$$
$$\begin{gather}\boldsymbol{P}^{C} ={-}\tilde{\kappa} \rho(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \rho(\boldsymbol{r}+\boldsymbol{c}_i\delta t), \end{gather}$$
while ![]() $\boldsymbol {F}^{B}$ and
$\boldsymbol {F}^{B}$ and ![]() $\boldsymbol {F}^{D}$ contribute to the pressure tensor as follows:
$\boldsymbol {F}^{D}$ contribute to the pressure tensor as follows:
 $$\begin{gather} \boldsymbol{P}^{B}={\pm} \frac{1}{6} \left[\psi(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \psi(\boldsymbol{r}+2\boldsymbol{c}_i\delta t) + \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \psi(\boldsymbol{r}-\boldsymbol{c}_i\delta t)\psi(\boldsymbol{r}+\boldsymbol{c}_i\delta t)\right], \end{gather}$$
$$\begin{gather} \boldsymbol{P}^{B}={\pm} \frac{1}{6} \left[\psi(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2} \boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \psi(\boldsymbol{r}+2\boldsymbol{c}_i\delta t) + \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \psi(\boldsymbol{r}-\boldsymbol{c}_i\delta t)\psi(\boldsymbol{r}+\boldsymbol{c}_i\delta t)\right], \end{gather}$$ $$\begin{gather}\boldsymbol{P}^{D} = \frac{\tilde{\kappa}}{2} \left[\rho(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \rho(\boldsymbol{r}+2\boldsymbol{c}_i\delta t) + \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \rho(\boldsymbol{r}-\boldsymbol{c}_i\delta t)\rho(\boldsymbol{r}+\boldsymbol{c}_i\delta t)\right]. \end{gather}$$
$$\begin{gather}\boldsymbol{P}^{D} = \frac{\tilde{\kappa}}{2} \left[\rho(\boldsymbol{r}) \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \rho(\boldsymbol{r}+2\boldsymbol{c}_i\delta t) + \sum_{i=0}^{Q-1} \frac{w_i}{\varsigma^2}\boldsymbol{c}_{i}\otimes\boldsymbol{c}_{i} \rho(\boldsymbol{r}-\boldsymbol{c}_i\delta t)\rho(\boldsymbol{r}+\boldsymbol{c}_i\delta t)\right]. \end{gather}$$
These expressions allow to compute the discrete pressure tensor with high accuracy. Figure 29 shows the distribution of the normal pressure, ![]() $P_{xx}$, in a flat interface simulation as computed from both the discrete and continuous pressure tensors,
$P_{xx}$, in a flat interface simulation as computed from both the discrete and continuous pressure tensors,
While the discrete evaluation method correctly results in a uniform pressure distribution throughout the domain, also across the interface, the continuous approximation evaluated using a finite differences approximation fails to do so, indicating errors due to higher-order terms. This points to the necessity of using the discrete pressure tensor instead of (E10) for evaluation of quantities such as surface tension and Tolman length in §§ 3.3 and 3.5.

Figure 29. Pressure distribution from a simulation at ![]() $T_r=0.36$, corresponding to
$T_r=0.36$, corresponding to ![]() $P_r=0.0022$ and
$P_r=0.0022$ and ![]() $\rho _l/\rho _v=10^3$. Black line, evaluation using the discrete pressure tensor; red line, evaluation using continuous pressure tensor; dashed blue line, density profile.
$\rho _l/\rho _v=10^3$. Black line, evaluation using the discrete pressure tensor; red line, evaluation using continuous pressure tensor; dashed blue line, density profile.
Appendix F. Analytical solution of layered Poiseuille flow
Solving the system presented in (4.1) and (4.2), one gets
with ![]() $a_l=-{\rho _l g}/{2\mu _l}$,
$a_l=-{\rho _l g}/{2\mu _l}$, ![]() $a_v=-{\rho _v g}/{2\mu _v}$, and
$a_v=-{\rho _v g}/{2\mu _v}$, and
Appendix G. Isothermal sound speed for other equations of states
Apart from the van der Waals equation of state in the main text, the present LBM formulation was also used to simulate the speed of sound for the three other cubic equations of state, Peng–Robinson (3.4), Riedlich–Kwong–Soave (3.7) and Carnahan–Starling (3.10), along with two equations of state proposed by Shan & Chen (Reference Shan and Chen1993),
with
while ![]() $P_0=\varsigma ^2\rho$. Corresponding critical densities
$P_0=\varsigma ^2\rho$. Corresponding critical densities ![]() $\rho _c$ and pseudo-temperatures
$\rho _c$ and pseudo-temperatures ![]() $\mathcal {G}_c$ are readily computed by solving the conditions at the critical point,
$\mathcal {G}_c$ are readily computed by solving the conditions at the critical point,
 \begin{equation} \left.\frac{\partial P_{SC}}{\partial \rho}\right|_{\mathcal{G}_c,\rho_c} = 0,\quad \left.\frac{\partial^2 P_{SC}}{\partial \rho^2}\right|_{\mathcal{G}_c,\rho_c} = 0, \end{equation}
\begin{equation} \left.\frac{\partial P_{SC}}{\partial \rho}\right|_{\mathcal{G}_c,\rho_c} = 0,\quad \left.\frac{\partial^2 P_{SC}}{\partial \rho^2}\right|_{\mathcal{G}_c,\rho_c} = 0, \end{equation}
which results in ![]() $(\mathcal {G}_c=-4,\rho _c=0.6931)$ and
$(\mathcal {G}_c=-4,\rho _c=0.6931)$ and ![]() $(\mathcal {G}_c=-7.389,\rho _c=1)$ for the pseudo-potentials (G2) and (G3), respectively. Figure 30 shows excellent agreement between simulations using the present model and theory for all equations of state. It is interesting to note that, in contrast to the conventional equations of state of the van der Waals type, the equations of state in (G1), (G2) and (G3) demonstrate higher speed of sound in the vapour phase than in the liquid. While this, by itself, does not contradict thermodynamics, it remains unclear which substances may feature such an unusual behaviour.
$(\mathcal {G}_c=-7.389,\rho _c=1)$ for the pseudo-potentials (G2) and (G3), respectively. Figure 30 shows excellent agreement between simulations using the present model and theory for all equations of state. It is interesting to note that, in contrast to the conventional equations of state of the van der Waals type, the equations of state in (G1), (G2) and (G3) demonstrate higher speed of sound in the vapour phase than in the liquid. While this, by itself, does not contradict thermodynamics, it remains unclear which substances may feature such an unusual behaviour.
Appendix H. Alternative reference pressure
The general framework introduced in the present publication allows for a wide range of pressure partitions. As mentioned in the main text, one possible choice is to set ![]() $P_0=P$ leaving only the surface tension contribution in (2.69). Another alternative is to follow the Enkog–Vlasov short- and long-range interaction partition leading, for the van der Waals equation of state, to
$P_0=P$ leaving only the surface tension contribution in (2.69). Another alternative is to follow the Enkog–Vlasov short- and long-range interaction partition leading, for the van der Waals equation of state, to
and
To better showcase the flexibility of the framework, flat interface simulations have been conducted using these alternative partitions. The resulting co-existence densities are shown in figure 31. For choices of partition leading to ![]() $P_0/\rho \neq {\rm const.}$, an additional constraint tied to the stability properties of the chosen lattice must be taken into account. For instance, for standard lattices used in the present work, it is well known that
$P_0/\rho \neq {\rm const.}$, an additional constraint tied to the stability properties of the chosen lattice must be taken into account. For instance, for standard lattices used in the present work, it is well known that ![]() ${P_0 \delta t^2}/{\rho \delta r^2}>{1}/{3}$ would lead to instabilities. Simulations shown in figure 31 were run with parameters guaranteeing
${P_0 \delta t^2}/{\rho \delta r^2}>{1}/{3}$ would lead to instabilities. Simulations shown in figure 31 were run with parameters guaranteeing ![]() ${P_0 \delta t^2}/{\rho \delta r^2}<{1}/{3}$.
${P_0 \delta t^2}/{\rho \delta r^2}<{1}/{3}$.