Article contents
Twin forces: similarity between rotation and stratification effects on wall turbulence
Published online by Cambridge University Press: 22 January 2024
Abstract
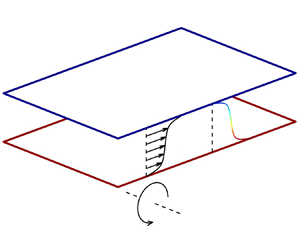
Can the similarity between rotation and stratification provide quantitative predictions for complex turbulence? In this work, we focus on plane Couette turbulence as the background flow, which allows us to eliminate the key differences between Rayleigh–Bénard and Taylor–Couette turbulence, and facilitates a quantitative mapping across many complex turbulent systems involving rotation, stratification and curvature effects. To characterize the separated or coupled effects of rotation and stratification, we introduce an overall Richardson number  ${Ri}_\chi$ which is the sum of the Coriolis Richardson number
${Ri}_\chi$ which is the sum of the Coriolis Richardson number  $Ri_\theta$ and the buoyancy Richardson number
$Ri_\theta$ and the buoyancy Richardson number  $Ri_T$. When the Prandtl number
$Ri_T$. When the Prandtl number  $Pr=1$, the heat and inertial-frame momentum transport almost coincide and mainly depend on
$Pr=1$, the heat and inertial-frame momentum transport almost coincide and mainly depend on  ${Ri}_\chi$ and the Reynolds number, regardless of the specific ratio between
${Ri}_\chi$ and the Reynolds number, regardless of the specific ratio between  $Ri_\theta$ and
$Ri_\theta$ and  $Ri_T$. When
$Ri_T$. When  $Pr$ varies, the weighted average
$Pr$ varies, the weighted average  ${Nu}_\chi$ of the transport coefficients can still remain approximately invariant in most cases. Furthermore, the large-scale structures in purely rotating and purely stratified cases exhibit strikingly similar features. These findings not only indicate a more reasonable analogy for the ultimate Taylor–Couette turbulence but also pave the way for developing new predictive models for natural and industrial processes.
${Nu}_\chi$ of the transport coefficients can still remain approximately invariant in most cases. Furthermore, the large-scale structures in purely rotating and purely stratified cases exhibit strikingly similar features. These findings not only indicate a more reasonable analogy for the ultimate Taylor–Couette turbulence but also pave the way for developing new predictive models for natural and industrial processes.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 3
- Cited by


