Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhao, Fuwang
Zeng, Lingwei
Bai, Honglei
Alam, Md. Mahbub
Wang, Zhaokun
Dong, You
and
Tang, Hui
2024.
Vortex-induced vibration of a sinusoidal wavy cylinder: The effect of wavelength.
Physics of Fluids,
Vol. 36,
Issue. 8,
Ding, Hao
Cheng, Ziyuan
Liu, Mingyue
Xiao, Longfei
and
Zhu, Shenglong
2024.
Effects of synthetic jet control parameters on characteristics of flow around a square cylinder at subcritical Reynolds number.
Ocean Engineering,
Vol. 309,
Issue. ,
p.
118577.
Garg, Ashish
Arif, Md. Reyaz
and
Hasan, Nadeem
2024.
Impact of free-stream orientation and thermal buoyancy on aerodynamic and heat transfer characteristics in mixed convective flow past an elliptical cylinder.
Physics of Fluids,
Vol. 36,
Issue. 7,
Aksoy, Muharrem Hilmi
Yagmur, Sercan
Dogan, Sercan
Goktepeli, Ilker
and
Ispir, Murat
2024.
Experimental study on cylinder wake control using forced rotation.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 246,
Issue. ,
p.
105662.
Shi, Xiaoyu
Alam, Md. Mahbub
Zhu, Hongjun
Ji, Chunning
Bai, Honglei
and
Sharifpur, Mohsen
2024.
Flow three-dimensionality of wavy elliptic cylinder: vortex shedding bifurcation.
Ocean Engineering,
Vol. 301,
Issue. ,
p.
117527.
Zhou, Yu
Hao, Jingcheng
and
Alam, Md. Mahbub
2024.
Wake of two tandem square cylinders.
Journal of Fluid Mechanics,
Vol. 983,
Issue. ,
Yue, Hao
Zhang, Hongfu
Ai, Yifeng
and
Zhou, Lei
2025.
Three-dimensional instability-inspired wake control on flow past a square cylinder via spanwise-distributed suction.
Ocean Engineering,
Vol. 337,
Issue. ,
p.
121910.
Shan, Longxiang
and
Zhang, Yang
2025.
Effects of geometric and wake characteristics on vortex-induced vibrations of a seal-whisker cylinder.
Physics of Fluids,
Vol. 37,
Issue. 1,
Afzal, Kamran
Younis, M. Yamin
Chuddher, Bilal Akbar
Ikram, Faraz
Ijaz, Asad
and
Alam, Md. Mahbub
2025.
Impact of cylinder corner modification on fluid dynamics and heat transfer: Corner cut size and cut angle.
Physics of Fluids,
Vol. 37,
Issue. 1,
Zhao, Hanghao
Zhang, Zhimeng
Ji, Chunning
and
Li, Xianghe
2025.
Hydrodynamics and flow perception mechanism of side-by-side Harbour seal whiskers in wake flow.
Bioinspiration & Biomimetics,
Vol. 20,
Issue. 6,
p.
066023.
Masud, Mahadi Hasan
Faisal, Abu Kaisar Md
Alam, Md. Mahbub
Rafi, Ashraful Islam
Islam, Rafsania
Ankhi, Israt Jahan
Bai, Honglei
and
Wang, Hanfeng
2025.
Corrugated airfoils for enhanced low-speed aerodynamics: A bio-inspired review.
Physics of Fluids,
Vol. 37,
Issue. 8,
Masud, Mahadi Hasan
Ankhi, Israt Jahan
Faisal, Abu Kaisar Md
and
Alam, Md. Mahbub
2025.
Translating marine biology into engineering: A review of biomimicry and its applications.
Ocean Engineering,
Vol. 339,
Issue. ,
p.
122108.
Kim, Minki
Yoon, Hyun Sik
and
Nair, Adarsh R.
2025.
The emergence of spanwise bluffness and transverse protrusion effects in aerodynamics of undulated geometries.
Physics of Fluids,
Vol. 37,
Issue. 5,
Zhang, Wenhui
Wang, Xiaodong
and
Chen, Yanli
2025.
Characteristics of the flow around two tandem cylinders of triangular and circular shapes.
Physics of Fluids,
Vol. 37,
Issue. 7,
Diao, Zhifan
Alam, Md. Mahbub
Wang, Enhao
Zhu, Hongjun
Ji, Chunning
and
Islam, Md
2026.
Effect of ellipsoid aspect ratio on wake.
Aerospace Science and Technology,
Vol. 168,
Issue. ,
p.
110772.
Alam, Md. Mahbub
and
Shi, Xiaoyu
2026.
Intelligent Robotics and Applications.
Vol. 16075,
Issue. ,
p.
581.
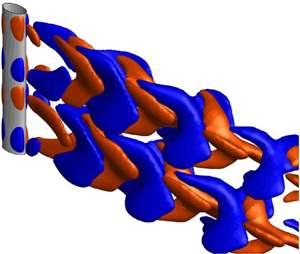
 $0.43 \le \lambda /{D_m} \le 8.59$, is considered with a wave amplitude of a/Dm = 0.048, where Dm is the hydraulic diameter of the wavy cylinder. Based on vortical structures, Strouhal number (St) and wake closure length (Lc), fluid forces, streamline topologies and spatio-temporal evolutions of the near wake, five distinct flow patterns (I–V) are identified depending on λ/Dm. The drag force reaches its minimum in pattern III, the fluctuating lift force is zero in flow patterns III and IV. Distinct from the classical flow where alternate vortex shedding occurs synchronously over the entire cylinder span, flow pattern IV has alternate vortex shedding over a one half-wavelength of the wavy elliptic cylinder, antiphased with that over the other half-wavelength, thus leading to zero fluctuating lift over one complete wavelength. A thorough comparison of the wakes is made between the wavy elliptic cylinder and wavy circular or square cylinder, distinguishing the underlying flow physics behind the salient behaviours observed.
$0.43 \le \lambda /{D_m} \le 8.59$, is considered with a wave amplitude of a/Dm = 0.048, where Dm is the hydraulic diameter of the wavy cylinder. Based on vortical structures, Strouhal number (St) and wake closure length (Lc), fluid forces, streamline topologies and spatio-temporal evolutions of the near wake, five distinct flow patterns (I–V) are identified depending on λ/Dm. The drag force reaches its minimum in pattern III, the fluctuating lift force is zero in flow patterns III and IV. Distinct from the classical flow where alternate vortex shedding occurs synchronously over the entire cylinder span, flow pattern IV has alternate vortex shedding over a one half-wavelength of the wavy elliptic cylinder, antiphased with that over the other half-wavelength, thus leading to zero fluctuating lift over one complete wavelength. A thorough comparison of the wakes is made between the wavy elliptic cylinder and wavy circular or square cylinder, distinguishing the underlying flow physics behind the salient behaviours observed.

