Article contents
Wing sweep effects on laminar separated flows
Published online by Cambridge University Press: 26 October 2022
Abstract
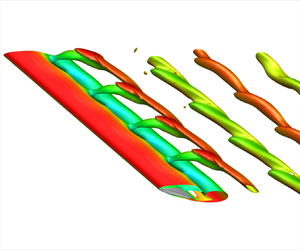
We reveal the effects of sweep on the wake dynamics around NACA 0015 wings at high angles of attack using direct numerical simulations and resolvent analysis. The influence of sweep on the wake dynamics is considered for sweep angles from  $0^\circ$ to
$0^\circ$ to  $45^\circ$ and angles of attack from
$45^\circ$ and angles of attack from  $16^\circ$ to
$16^\circ$ to  $30^\circ$ for a spanwise periodic wing at a chord-based Reynolds number of
$30^\circ$ for a spanwise periodic wing at a chord-based Reynolds number of  $400$ and a Mach number of
$400$ and a Mach number of  $0.1$. Wing sweep affects the wake dynamics, especially in terms of stability and spanwise fluctuations with implications on the development of three-dimensional (3-D) wakes. We observe that wing sweep attenuates spanwise fluctuations. Even as the sweep angle influences the wake, force and pressure coefficients can be collapsed for low angles of attack when examined in wall-normal and wingspan-normal independent flow components. Some small deviations at high sweep and incidence angles are attributed to vortical wake structures that impose secondary aerodynamic loads, revealed through the force element analysis. Furthermore, we conduct global resolvent analysis to uncover oblique modes with high disturbance amplification. The resolvent analysis also reveals the presence of wavemakers in the shear-dominated region associated with the emergence of 3-D wakes at high angles of attack. For flows at high sweep angles, the optimal convection speed of the response modes is shown to be faster than the optimal wavemakers speed suggesting a mechanism for the attenuation of perturbations. The present findings serve as a fundamental stepping stone to understanding separated flows at higher Reynolds numbers.
$0.1$. Wing sweep affects the wake dynamics, especially in terms of stability and spanwise fluctuations with implications on the development of three-dimensional (3-D) wakes. We observe that wing sweep attenuates spanwise fluctuations. Even as the sweep angle influences the wake, force and pressure coefficients can be collapsed for low angles of attack when examined in wall-normal and wingspan-normal independent flow components. Some small deviations at high sweep and incidence angles are attributed to vortical wake structures that impose secondary aerodynamic loads, revealed through the force element analysis. Furthermore, we conduct global resolvent analysis to uncover oblique modes with high disturbance amplification. The resolvent analysis also reveals the presence of wavemakers in the shear-dominated region associated with the emergence of 3-D wakes at high angles of attack. For flows at high sweep angles, the optimal convection speed of the response modes is shown to be faster than the optimal wavemakers speed suggesting a mechanism for the attenuation of perturbations. The present findings serve as a fundamental stepping stone to understanding separated flows at higher Reynolds numbers.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
Footnotes
Current affiliation: School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China.
References
- 11
- Cited by



