1. Introduction

The permanent polar caps on Mars are recognizable from the topography as domes rising above the surrounding layered terrain (Reference ZuberZuber and others, 1998; Reference SmithSmith and others, 1999; Reference Schenk and MooreSchenk and Moore, in press; see also the extensive review by Reference CliffordClifford and others, 2000). One has to distinguish them from the seasonal caps, whose visible extent varies through the Martian year and which are probably surface layers of solid carbon dioxide. There are such seasonal carbon dioxide surface layers in both the north (Reference Haberle and JakoskyHaberle and Jakosky, 1990; Reference KiefferKieffer, 1990) and the south (Reference Herkenhoff and MurrayHerkenhoff and Murray, 1990; Reference Paige, Herkenhoff and MurrayPaige and others, 1990). On the other hand, it is plausible to suppose that the north and south permanent polar caps of Mars are made of water ice, possibly with a substantial admixture of rock particles, but this is not yet firmly established. Water ice is observed in the north (Reference KiefferKieffer, 1990), but an alternative hypothesis that the entire thickness of the south polar cap is solid carbon dioxide seems to fail on mechanical grounds; Reference Nye, Durham, Schenk and MooreNye and others (2000) concluded that such a material is far too weak to support a cap of the observed height of 3000 m for the necessary time of 10⁷ years.

The flow model used in Reference Nye, Durham, Schenk and MooreNye and others (2000) was comparatively crude in its treatment of the effect of temperature on the flow, but the simplification was justified because the solid-carbon-dioxide hypothesis gave lifetimes that were orders of magnitude too small even on the most extreme assumptions. However, to use such a flow model to make a fuller test of the assumption that both caps are made of water ice requires a more careful treatment of the effect of temperature, and that is the purpose of the present paper.

Reference Budd, Jenssen, Leach, Smith and RadokBudd and others (1986) took full account of the complex topography of the north cap by a numerical approach, and related their results to a steady state. In contrast, the present paper uses analytical methods to study an ice cap having circular symmetry and does not assume a steady state. It calculates what flow would occur in a cap of carefully chosen profile in the absence of any accumulation or ablation (it being supposed that there has been none of significance in the relevant period). The central parts will tend to fall, the outer parts will rise, and at the same time the perimeter will move outwards.

A crucial question is what profile to assume, because slight differences in the profile result in totally different distributions of the rate of change of thickness. The profile chosen will, in fact, be close to, but not identical with, that of the Reference VialovVialov (1958) model, as seen in Figure 1. The rather similar Reference NyeNye (1959) model is less appropriate for comparison here because it is based on a sliding law rather than on a flow law. Both the Vialov and the Nye model assumed a steady state and a uniform distribution of accumulation; there was accumulation over the cap but no ablation. The rate of discharge of ice across the outer edge was therefore finite although the thickness was zero; as a result, the velocity at the edge was infinite. For a terrestrial ice cap that is bounded by the sea, perhaps this singularity in the model could be tolerated; it corresponds to concentrating all the ablation into the perimeter and not allowing the cap to expand sideways. For an ice cap that ends on land and spreads laterally under its weight, it is not appropriate.

Fig. 1. Comparison of two profiles, the Reference VialovVialov (1958) model and the present model, both with n = 1.8.

The present model is quite different in conception, in that it calculates for zero accumulation and ablation and derives an evolving profile (a changing shape) from a similarity hypothesis. Most notably, it avoids the edge singularity in the above models and allows the cap to spread laterally.

2. The Model

The required solution of the flow equations, a similarity solution, was introduced into glaciology by Reference HalfarHalfar (1981) for two-dimensional flow and Reference HalfarHalfar (1983) for radial flow, as here. Reference HindmarshHindmarsh (1990) has discussed the two-dimensional solution. Here, prompted by the latter paper, we deduce the radial-flow solution from a similarity hypothesis, rather than simply state it. Our model is then essentially the same as that of Reference HalfarHalfar (1983), but with two additions. First, it is found possible to include isostatic depression of the base with minimal change in the mathematics; second, we take account of the effect on the flow law of the variation of temperature with depth and with time.

At radius r and time t the thickness is h(r, t) (Fig. 2a). The thickness at the centre h(0, t) is denoted by h ₀(t), and the radius of the base is r ₀(t). The base, originally horizontal, is depressed by the weight of the ice by a fraction f of the ice thickness, that is by fh(r, t), so that the elevation of the upper surface is (1 − f)h(r, t). Define a scaled radial co-ordinate ρ = r/r ₀(t) and a scaled thickness η (Fig. 2b)

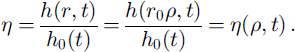
We look for a solution of the flow equations in which η = η(ρ), independent of t; that is, the scaled shape keeps the same analytical form. It does not remain geometrically similar (Fig. 3); the aspect ratio changes.

Fig. 2. Notation for the model cap: (a) dimensional lengths, (b) scaled dimensionless lengths.

Fig. 3. The thickness distrihution for n = 1.8 at three successive instants t = 0, 2t₀, 4t₀. The intersection point of successive curves moves outwards as the profile collapses, because ∂h/∂t = 0 at fixed ρ not fixed r. The value of r for which ∂h/∂t = 0 at t = 0 is indicated.

Let q(r, t) be the radial flux (volume per unit time crossing an area of height h and unit circumferential length). By conservation of volume

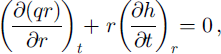
the second term of which is

Because the overall volume is fixed and η = η(ρ), , and hence . Since ρ = r/r ₀,

Thus, from Equation (3)

and Equation (2) becomes, in terms of ρ

The crucial step is in Equation (5), where (∂/∂t) _r is converted to d/dρ. Equation (6) may now be integrated with respect to ρ at constant t; thus

Dividing by ρ, and demanding that q = 0 at ρ = 0 for all t, sets g(t) ≡ 0, so that

We now introduce a flow law of the form

where is the uniaxial compression rate of polycrystalline ice under uniaxial compressive stress σ, A _D and n are constants, Q is the activation energy, R _G is the gas constant (8.3143 J K⁻¹ mol⁻¹) and T is the absolute temperature. The corresponding relation for the simple shear rate under shear stress τ is

It is convenient to assume at first that the temperature is uniform in space and constant with time, but later this restriction will be removed. Taking the flow of the cap to be predominantly by horizontal shearing and assuming the slope α of the top surface to be small, we have at given radius and time (Nye, Reference Nye1952)

where

ρ′ is the density, and the full stop in Equation (11) separates the time-dependent part from the ρ-dependent part. ∂h/∂r and dη/dρ are negative. Note that the flow law of ice at the appropriate temperature is included in the constant C. At the extreme edge the slope becomes infinite, and Relation (10) must break down; it should be replaced by different physics, but because the region affected is very narrow we shall ignore this defect. A similar problem arises in all models of this kind. In view of Equation (8) the equation to be integrated is therefore

After division by the variables may now be separated to give

and

where K is a constant.

The thickness distribution will follow from integrating Equation (14):

First, use for the upper limits η = 0 at ρ = 1, to yield the value of K as

Then, on integration, the scaled thickness distribution is

as found by Reference HalfarHalfar (1983) for the case f = 0. It is fortunate that non-zero f makes no difference to this equation.

Integration of Equation (15) gives the time dependence. It is convenient to think of t = 0 as the present, when the central height is H ₀ = h ₀(0) and the radius of the cap is R ₀ say. Then , and Equation (15) becomes

This integrates to give the decay of the central height as

with, using Equation (16),

t = −t ₀ is the time at which the central height is asymptotically infinite (Fig. 4). Equation (19) will be central in what follows.

Fig. 4. The decay of the central thickness with time.

Since is constant the corresponding equation for the expansion of the outer rim is

and the aspect ratio diminishes according to

In Equation (19) R ₀ and H ₀ are observable quantities, C can be estimated as discussed below, and so, with an estimation of the isostatic fraction f, t ₀ can be calculated. In the model the cap spreads out from an initial delta-function shape at t = −t ₀. In Figure 3, h(r) is computed at successive times t = 0 (the present) and 2t ₀, 4t ₀ (in the future) by using Equations (17), (18) and (20). Reference HalfarHalfar (1983) has shown that the resulting evolving profile is stable against all perturbations that preserve the total volume. That is the justification for using this special profile, and its decay with time, as a model of the real situation. Whatever the real history of the cap may have been, the profile would have settled down quite quickly (in a time much less than t ₀) to the steady mode calculated; an analogous situation occurs when syrup falls from a spoon on to a plate to form a spreading dome. t ₀ is the age of the model cap. Making the assumption that the real caps have evolved to their present shapes by non-Newtonian viscous spreading, we shall interpret t ₀ as the age of the real cap, even though it began in a different way from the model cap.

3. Estimation of C

By taking C, which incorporates the flow law, as a constant, the calculation has assumed that the temperature is both uniform in space and constant with time. We shall continue to assume that the surface temperature remains constant with time (in the absence of reliable evidence to the contrary), thus ignoring the obliquity cycle of 1.25 × 10⁵ years (Reference CliffordClifford and others, 2000), but we wish to take explicit account of the fact that the temperature is non-uniform with depth by using a parallel-sided slab model. Specifically, with z measured downwards from the surface, we assume a non-uniform temperature gradient that conducts the geothermal heat flux ϕ upwards:

The gradient is non-uniform because the thermal conductivity k depends upon temperature. (In terrestrial ice caps an additional non-uniformity is caused by advection due to the downward vertical motion of the ice, but in the present model the slowness of the downward motion makes such an effect negligible.) The flow law now depends on depth.

If u is the outward velocity at depth z we have, at radius r, where the surface slope is α,

Hence, assuming zero velocity on the bed,

A further integration gives the discharge as

It is useful to define an effective temperature T _eff as the uniform temperature that would give the same discharge as the actual non-uniform temperature. If T(z) in the above integrand is replaced by a constant T _eff, the double integral becomes exp(−Q/R _G T _eff). h ⁿ⁺²/(n + 2), as used in Equation (12). Thus T _eff is given by

To apply Equation (19), where C is constant, it is necessary to choose a single value for T _eff that is representative of the whole cap and indeed of its whole history. This means a single representative value of h for the thermal calculation. Therefore, to choose h we first average η over the area of the ice cap — for n = 1.8 (see below) the average is 0.6766 — and hence, using the observed central elevation with an assumed f, we find the average thickness at t = 0 (the present). Then, to take some account of the greater thickness in the past, we scale it up by a factor corresponding to halfway through the period of interest, t = −t ₀ to 0, found from Equation (18) as 2^2/(5n+3); for n = 1.8 this amounts to an increase of 12% (the decay curve in Figure 4 is quite flat).

Having chosen h in Equation (25), the next task is to evaluate the function T(z) using Equation (22). The temperature dependence of the thermal conductivity of pure ice is well represented by the relation (Hobbs, Reference Hobbs1974, p. 358)

By integration of Equation (22) downwards from the surface, where T = T _s,

To invert this to find T(z) we select a desired value z ₀ and solve the equation z ₀ − z(T) = 0 numerically for T, by Newton’s method, given the gradient z′(T) = k(T)/ϕ, from Equation (22). This gives T(z) for a chosen value of ϕ. The double integral in Equation (25) is evaluated by Simpson’s rule, and hence T _eff, is found.

The numerical consequences of applying these results, especially Equation (19), to the Martian caps will be discussed in section 5. The next section will trace some formal consequences of the model.

4. Remarks about the Flow Solution

5. Numerical Results for the Mars Caps

The central elevation is 2950 m for both caps (Reference ZuberZuber and others, 1998; Reference Schenk and MooreSchenk and Moore, in press); for the north cap T _s = 175 K; for the south cap, T _s = 155 K. For the radius of the north cap, whose outline is rather irregular and uncertain, we adopt the ice volume reported by Reference ZuberZuber and others (1998) (1.5 × l0⁶ km³ for a mean value of the isostatic fraction f) and place it in a cap of central elevation 2950 m with the profile of Equation (17) (with n = 1.8, as justified below). This gives R ₀ = 430 km. For the south cap we take R ₀ = 225 km (Reference Schenk and MooreSchenk and Moore, in press). For the north cap Reference ZuberZuber and others (1998) suggest that f lies between 0.15 and 0.29. For the south cap we assume the same range. Other values adopted are: ρ′ = 920 kg m⁻³, g = 3.72 m s⁻².

The Martian heat flux has not been measured. A nominal value often assumed, by analogy with the Earth, is ϕ ₀ = 30 mW m⁻² and we express the flux used in the computation as a multiple λ of this; thus ϕ = λϕ _0. With λ = 1 and f = 0.15, T _eff = 196 K for the north cap and 174 K for the south cap. With λ = 1 and f = 0.29 the corresponding temperatures are 201 and 179 K (giving an overall mean of 188 K).

The physical mechanism of the deformation changes with the applied stress. The flow law of Reference Durham, Kirby and SternDurham and others (1997), namely, A _D = 1.26 × 10⁵ Mpa⁻ⁿ s⁻¹, n = 4, Q = 61000 J mol⁻¹, is applicable for higher stresses, where dislocation creep mechanisms dominate, while that of Reference Goldsby and KohlstedtGoldsby and Kohlstedt (1997), with n = 1.8, is appropriate at lower stresses where mechanisms such as grain-boundary sliding become favoured. The latter authors find that creep rate depends on grain-size d with an exponent extrapolating their results to a grain-size of 1.0 mm (see below) gives A _D = 62 MPa⁻ⁿ s⁻¹, Q = 49 000 J mol⁻¹. We shall assume that both laws operate for all stresses, and that the total deformation rate is the sum of the rates from the two different processes. However, at low stresses the Goldsby and Kohlstedt mechanism will be more effective and the law will appear to have n = 1.8. Thus, looking first at the curve in Figure 6 for d = 1 mm, we see the result of taking the total shear strain rate as the sum of the rates given by the two laws with n = 1.8 and 4, respectively. Explicitly, if subscript “i” refers to the two laws,

The factor is 4.7 for n = 1.8 and 15.6 for n = 4.)

Fig. 6. The result of combining two flow laws for n = 1.8 and n = 4. The basal shear stresses estimated for the two caps are indicated.

The change in slope from 1.8 to 4 in this log-log plot occurs at the shear stress where the two rates are equal. For T = 199 K (north cap) the crossover is at 0.49 MPa, while for T = 177 K (south cap) it is at 0.74 MPa. These values must be compared with the actual stresses in the caps. The shear stress near the base of the cap at a radius where the thickness is may be estimated as

Both values are well below the crossover stresses, and are therefore in the region where the flow law with n = 1.8 should apply. The curve in Figure 6 for d = 10 mm shows that this conclusion still holds for a larger grain-size. We also note that Reference Durham, Kirby and SternDurham and others (1992) found that up to 10% of added quartz sand has little effect on the flow properties of ice. We shall therefore use the n = 1.8 law, but recognizing that there are still uncertainties, which we shall refer to later; these arise primarily from the unknown preferred orientation of the crystals in relation to the stress configuration. The flow law recommended by Reference PatersonPaterson (1994) with n = 3 is intermediate between the above two laws.

Figure 7 shows a semi-log plot of t ₀ against λ using Equation (19). A high value of λ means greater heat flux, higher temperature at depth, weaker ice, and so a shorter lifetime t ₀. Lines are shown for the two extreme values of f. The lines for the two caps are not very different, and the effect of changing f is not great.

Fig. 7. The age to of the caps as a function of the thermal flux, expressed as a multiple λ of 30 mW m⁻². Full lines: north cap; thin lines: south cap.

In quoting observational evidence for the age of the caps one must distinguish them from the so-called layered deposits which appear to underlie them. The layered deposits are more extensive than the caps, especially in the south, and consist of horizontal layers of varying relative abundance of dust and water ice, which are thought to reflect climatic variations. The polar caps, on the other hand, are recognizable from their dome-shaped topography and high albedo. Although there are extensive observations, reviewed by Reference CliffordClifford and others (2000), the precise relation between these two geologic units remains far from clear. Crater densities on the layered deposits indicate their ages. Reference CliffordClifford and others (2000) quote observational evidence for an age of the exposed surface of the deposits in the north of less than about 10⁵ years, and in the south of 7–15 × 10⁶ years. But for the caps themselves we must distinguish between the age of their surfaces and how long the bulk of their material has been there. They are very sparsely cratered and we shall tentatively assume they are 10⁶ to 10⁸ years old.

It is striking that, if we select the mean value t ₀ = 10⁷ years in Figure 7, the A values for both caps fall into a fairly narrow band about λ = 1.1, although it would not have been surprising if A had been somewhat different from this. With t ₀ = 10⁸ years the values centre on λ = 0.6.

It is as well to end on a note of caution. Strain rates in glaciology have always been notoriously difficult to calculate ab initio, because of uncertainties in extrapolating laboratory measurements to low strain rates, and in the effect of factors like grain shape, grain-size, preferred crystallographic orientation, recrystallization and bubbles. In the present problem, where grain-boundary effects are dominant, grain-size is perhaps the most troublesome unknown. Observations of the surface of the north cap (Reference KiefferKieffer, 1990) suggest a grain-size of 0.1 mm or more, and we have assumed 1 mm as a reasonable value at depth. A larger grain-size would lead to a smaller strain rate , and the value of t ₀ would be correspondingly increased; for example, d = 10 mm instead of 1 mm would raise all the curves in Figure 7 by a factor 10^1.4 = 25.1. The λ values for t ₀ = 10 and 10 years would then fall in bands about λ = 2.0 and 1.4 (instead of 1.1 and 0.6).

In Figure 7 the north cap is rather younger than the south cap. The reason is revealed by using Equations (19) and (12) to find the ratio of their ages, taking n, f and H ₀ to be the same for both caps:

where the subscripts “N” and “S” refer to the two caps, and T _N and T _S are the effective temperatures for λ = 1 and a mean value of f. The first factor on the right is 6.13: larger R ₀ (north cap) means lower slopes and therefore smaller stresses and strain rates and longer times. The second factor on the right is 1/40.5: higher temperature (north cap) means higher strain rates and shorter times. The temperature effect is the greater of the two opposing influences, so the calculated lifetime of the north cap is shorter by a factor 40.5/6.13 = 6.6. Reference CliffordClifford and others (2000) quote observations implying that the layered terrains in the north are two orders of magnitude younger that those in the south. If this difference for the layered terrains also applies to the polar ice caps, the flow model has predicted an age ratio with the same sign as that observed, but rather smaller in magnitude.

Looked at differently, Figure 7 places a constraint on the heat flux; it cannot be greater than λ ≈ 2.5, because that would imply that the ice caps were younger than about 10⁵ years old. As regards the possibility of basal melting (Reference CliffordClifford, 1987), the present model finds that this would be achieved with the present thicknesses at the centres if the heat-flux factor were λ = 2.1–2.5 (north cap) and 2.7–3.2 (south cap).

In summary, Figure 7 shows that the dimensions and surface temperature of both caps are consistent with a heat flux not far removed from that of the Earth (λ =1), which is what is usually assumed for Mars. This supports the hypothesis that the material of both caps is flowing water ice, with an unknown amount of rock debris added.