Introduction

It has become quite common to accumulate data on temperature distributions in glaciers. There is occasional interest in analyzing such data to obtain a portrayal of a heat flux distribution. This latter information may be of particular interest near discontinuities, either natural such as crevasses or man-made such as slits, trenches, or excavations.

The experimentally observed temperature data near a glacier crevasse in the ice sheet of northern Greenland have been reported in a previous paper (Reference PingsPings, 1961). General glacioIogical characteristics of the area were discussed by M. F. Meier and co-workers (Reference MeierMeier and others, 1957; Reference MeierMeier, 1958). The isotherms previously reported were obtained by repeated smoothing of experimental data to obtain temperature distributions that were continuous with respect to both time and spatial variation. As a final exercise with those previous data we reported a net of heat flux lines constructed orthogonal to one of the sets of isotherms. Although this latter technique is elegant mathematically, it is subject to substantial error as a graphical tool. The drawing of a given heat flux line is subject to cumulative error and, at best, is no better than visual judgment of orthogonality.

Such constructions are also limited by assumptions of constant, isotropic values of the thermal conductivity. It is not apparent how one might easily modify the method to account for anisotropie behavior of the thermal conductivity or the variation of thermal conductivity with either temperature or position. We suggest in this paper a technique which is quite general and which is reasonably easily applied to the analysis of experimental temperature data.

Components of the Heat Flux Vector

In the present discussion only two independent spatial variables are included. The data were all collected in a plane normal to the length of the crevasse, and our entire analysis is idealized to temperature distribution and heat flow in a plane. The generalization to three dimensions should be obvious. In the following, y is the vertical coordinate measured downward from the surface, and x is the horizontal coordinate with positive direction pointing away from the crevasse.

In a single crystal the components of the heat flux vector are related to the temperature gradient (Reference NyeNye, 1957, ch. 11) by the following:

where repeated suffixes indicate summation. The k _ij ’s are the coefficients of thermal conductivity, constituting a second-rank tensor. It may be shown (Reference NyeNye, 1957; Reference MillerMiller, 1960) that the k _ij tensor is not only symmetric, but that the off-diagonal terms are all identically zero if the (x, y, z) coordinate system is chosen to coincide with the principal axes of the crystal. If there exists systematic variation in the orientation of the crystals in a gross body such as a glacier, it would obviously be impossible to select a fixed coordinate system such that its axes were everywhere parallel to the principal axes of the crystals. Nevertheless, if all the terms in the conductivity tensor were known at each point, it would be possible to compute the components of the heat flux vector from a knowledge of the temperature gradient using equation (1)

If a macroscopic body is comprised of randomly orientated crystals, the averaged conductivity tensor contains off-diagonal terms of zero and identical diagonal terms comprised of appropriately weighted averages of the components of the single crystal tensor. For the ice body which we consider here, Hoerni (Reference MeierMeier and others, 1957) found some indications of regions of preferred crystal orientation. However, he regarded the evidence as inconclusive. In subsequent discussion we therefore treat the glacier as isotropic. For the two-dimensional problem it will be convenient to represent the heat flux vector in terms of its components.

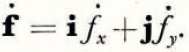
With the stated assumption of isotropy, each of these components can be idengified with a single temperature gradient:

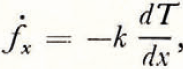
The above expressions may be combined to yield the following description for the heat flux vector, its magnitude, and its orientation in space:

Our present computational scheme involves simply the evaluation of the two derivatives, dT/dx and dT/dy in the two-dimensional region of interest. We report these results for only one of the sets of temperature measurements reported in the previous publication, namely the temperature data collected on 16 August 1955 (Reference PingsPings, 1961). Those two-dimensional temperature data were replotted in a series of graphs, one set giving T versus x along lines of constant y, and a second set giving T versus y along lines of constant x. Incidentally, these graphs, or their substantial equivalents were actually by-products of the smoothing operations that went into the original preparation of the two-dimensional isotherm maps. Since those smoothing operations would usually be a necessary step in the treatment of temperature data obtained experimentally in the field, it should not normally be necessary to prepare them separately for purposes of heat flux computations suggested in this paper.

Once the above graphs had been prepared, it was a simple matter to obtain the derivatives required at all points in space by graphical techniques. We made these computations by establishing the slope of the line tangent to the temperature curves at each point of interest. Since the data used for this computation were already smoothed with respect to spatial variations, the values obtained for the derivatives were reasonably smooth and consistent. Results of the differentiation are shown in Figures 1 and 2. Dashed lines indicate regions where we felt the original temperature data were either in doubt or rather sparsely distributed.

Fig. 1. Complied values of dT/dx

Fig. 2. Computed values of dT/dy

It might be recalled that the vertical and horizontal components of the heat flux vector are proportional to dT/dx and dT/dy. It is interesting to note several qualitative characteristics of the heat flux distribution apparent from inspection of these two graphs: (1) the horizontal component of a heat flux vector becomes smaller and presumably approaches zero at distances progressively farther from the crevasse; (2) there exists a line of zero value for the vertical component of the heat flux, with that component being directed downward above that locus and upward below it; (3) there is a substantial component of the heat flux vector directed into the ice body from the crevasse wall, whereas the vertical component of the heat flux vector appears to be relatively small immediately adjacent to the crevasse; (4) although the original temperature data within the crevasse were somewhat less reliable than those obtained from the ice body, the information available seems to indicate a smooth continuation of the dT/dx values from the ice mass into the crevasse air space.

Synthesis of Heat Flux Vectors

Figure 3 shows the heat flux vectors which were synthesized from the computed components using equations (5), (6) and (7). Actually, the values reported are

, and it was, therefore, not necessary to make any assumption as to the numerical magnitude of the thermal conductivity. As an example of actual flux magnitude, using the value of thermal conductivity reported by Reference Van DusenVan Dusen (1929) of k = 50×10⁻⁴ cal. cm.⁻¹ ° C.⁻¹ sec.⁻¹, then, at the point (x = 2 m., y = 4.4 m.), the magnitude of the heat flux vector is 3.15 cal. m.⁻² sec.⁻¹.

Fig. 3. Computed values of the heat flux vectors,

We are certainly not suggesting that the above detailed conclusions are generally indicative of heat transfer adjacent to the crevasse. Rather the comments are offered as examples of the type of information that can be obtained from analysis of the computed components of the heat flux vector.

Acknowledgements

The author acknowledges the assistance and interest of the U.S. Army Cold Regions Research and Engineering Laboratory. Kenneth Larson assisted in the computation.