Introduction
The shape, extent and internal structures of polar ice sheets are influenced by climate, and evolve in response to climate change. Glacial ice also contains impurities and isotopic signatures that are determined by environmental factors. Analysis of the geochemical content of polar ice recovered in ice cores is a well-established way to provide highly resolved temporal information about climate history (e.g. Reference Dansgaard, Johnsen, Clausen and GundestrupDansgaard and others, 1973; Reference AlleyAlley and others, 1997; Reference MayewskiMayewski and others, 1997; Reference TaylorTaylor and others, 2004). Ice-flow calculations combined with detailed geophysical measurements made in the vicinity of an ice-core site are fundamental glaciological contributions to ice-core paleoclimate programs. For example, before drilling begins, modelled depth–age relationships allow identification of sites with acceptable maximum age or satisfactory temporal resolution in a particular age range. The accuracy of such determinations is limited by factors that include inadequate knowledge of the flow field and the accumulation rate history. Once various core properties have been sampled, ice-flow models are important tools for interpretation of the ice-core record. For example, Reference Cuffey, Clow, Alley, Stuiver, Waddington and SaltusCuffey and others (1995) used borehole temperature measurements and an ice-flow model to calibrate the stable-isotope ‘thermometer’ and to infer the magnitude of surface temperature change that occurred with the Wisconsin– Holocene transition in central Greenland. To the extent that the model accurately describes the controlling physics, mismatches between measured and modelled depth–age scales can reveal differences between the assumed and actual accumulation history. Ice-flow models can calculate the cumulative vertical strain experienced by layers during burial and subsequent flow. The calculated fractional thickness of any layer in the ice core relative to its initial thickness (in ice equivalent units) is often called the ‘thinning function’. Reference Cutler, Raymond, Waddington, Meese and AlleyCutler and others (1995) and Reference Cuffey and ClowCuffey and Clow (1997) used modelled thinning functions to infer accumulation rate histories from the measured spacing of annual layers in the Greenland Ice Sheet Project 2 (GISP2) ice core.
An ice-core paleoclimate project was carried out at Taylor Dome, East Antarctica, (Fig. 1) during the 1990s. In 1993/94, a 554 m ice core to bedrock was recovered from a site approximately 3 km from the ice divide. The resulting paleoclimate record (Reference MayewskiMayewski and others, 1996; Reference SteigSteig and others, 1998, Reference Steig2000; Reference Grootes, Steig, Stuiver, Waddington, Morse and NadeauGrootes and others, 2001) spans a complete ice-age cycle with good resolution, and extends (though highly compressed) through two or more glacial cycles. Prior to core recovery, geophysical and geochemical surveys were performed to select an ice-core site (Reference Grootes, Steig and MasseyGrootes and others, 1991, Reference Grootes, Steig and Stuiver1994; Reference Waddington, Morse, Balise and FirestoneWaddington and others, 1991, Reference Waddington, Morse and Clow1994; Reference Grootes, Steig and MasseyGrootes and Steig, 1992; Reference Morse and WaddingtonMorse and Waddington, 1992, 1993). These studies concluded that ice in the Taylor Dome core probably fell as snow within 3 km of the core site and the site has conditions that are conducive to good preservation of geochemical records on decadal timescales or longer. The mean annual surface temperature is below –40°C (Reference Waddington and MorseWaddington and Morse, 1994), and the snow accumulation rate ranges from ~0.02 to 0.2 m a–1 ice equivalent across the dome (Reference MorseMorse and others, 1999). In addition to these observations, ice thickness, surface topography and ice temperature measurements were presented by Reference MorseMorse (1997). In this paper, we report on ice motion measurements at Taylor Dome and ice-flow models used to augment the climatic interpretation of the ice-core measurements.
Fig. 1. Map showing Antarctica (inset) and the location of Taylor Dome in relation to the Ross Ice Shelf and McMurdo Dry Valleys. The dot marking the primary Taylor Dome drill site is enclosed in a box that shows the region of Figure 2.
Ice Motion Measurements
Ice motion measurements provide strain-rate data needed to constrain ice-flow models. We established a strain network consisting of 253 marker poles (most of which are shown in Fig. 2), to measure the surface pattern of ice deformation. We first established a reconnaissance network that covered a large area at coarse (nominally 2.5 km) spacing. We then halved and quartered the grid spacing to improve the spatial resolution in the vicinity of the selected ice-coring site and along its flowline. Due to longitudinal stress coupling, flow conditions as far as ten ice thicknesses upstream and downstream can affect ice flow near the core site (e.g. Reference RaymondRaymond, 1983);our survey spanned this range. Each marker was surveyed at least twice over six successive field seasons. In 1990–94, the markers were surveyed by traditional optical techniques, using a Wild T1000 theodolite and DI5S electronic distance meter (EDM). In 1994/95 and 1995/96, we used Trimble 4000SST GPS (global positioning system) receivers and Trimble GPSurvey (WAVE 2.00b) post-processing software to measure the position and motion of one central marker relative to two nearby stationary (bedrock) benchmarks and another distant GPS base station, and to measure positions of other markers relative to that central marker.
Fig. 2. Ice surface elevation contours at 20m intervals from airborne surveys conducted during 1991/92 (Reference MorseMorse, 1997). Ice motion marker poles are shown as dots. Fixed bedrock markers are near (x, y) = (20,0) and (48,10). The primary ice-core site is near (15,19) in the region of densely spaced markers. The dashed box around the core-site region defines the region shown in Figure 3. An additional dense network of markers was emplaced and surveyed in the vicinity of a secondary core site at ‘Taylor Mouth’, (43,11). Velocities of these markers are analyzed by Waddington and others (in press).
Normally, even with modern GPS software, velocities are found using the reduction-to-epoch approach, in which all observations are interpolated or extrapolated to two or more distinct times or epochs at which the marker positions are calculated. The calculated positions are then differenced to give velocities averaged over the time interval. Because of the large scale of the Taylor Dome network, the limited time for surveys in each field season and the evolving focus of the motion survey, only portions of the entire net were surveyed in any one field season. In addition, the surveyed portions could not always be tied to control points until subsequent years, and the exact combination of observations was not repeated. Therefore, we could not use the reduction-to-epoch approach. Instead, we developed a procedure that uses all the survey observations to solve simultaneously for the positions and velocities of all the markers. This approach was pioneered by Reference Steffensen and JohnsenDahl-Jensen and others (1986). Using a large set of redundant observations, they directly solved for a set of parameters describing the trajectory of a single marker. Our method, described in the Appendix, extends the method by simultaneously finding parameters describing the trajectories of many markers. Discrepancies among redundant observations are balanced among the observations in a least-squares sense. Reference ChadwellChadwell (1999) also described a procedure that could find trajectory parameters using a standard least-squares formulation. In a standard least-squares formulation, the so-called normal equations (e.g. Reference Press, Flannery, Teukolsky and VetterlingPress and others, 1986, p. 23) are solved by finding the inverse of a square matrix; however, this matrix can be singular or near-singular, subjecting the solution to serious error, or causing the solution to fail. Our approach is more robust, because we solve for marker-trajectory parameters using singular value decomposition (SVD) (e.g. Reference Press, Flannery, Teukolsky and VetterlingPress and others, 1986, p. 59) which consistently gives the best solution in a least-squares minimization sense, while avoiding singularities and round-off issues (see Equation (A6) in the Appendix).
Reference MorseMorse (1997) gives a detailed discussion of the survey data reduction. First we solved for the relative marker positions in each of the seasons, to remove erroneous optical observations identified as outliers of the statistical distribution of discrepancies. The remaining observations from all seasons were then combined to simultaneously determine the marker trajectories. Refraction due to temperature gradients in the near-surface atmosphere causes optically surveyed targets to have an apparent vertical offset (e.g. Reference PatersonPaterson, 1955; Reference Moffitt and BouchardMoffitt and Bouchard, 1982). We applied small distance-dependent corrections to the observed vertical angles (e.g. Reference RasmussenRasmussen, 1986) to remove this effect (see Equation (A13)). We used a value of –1.5 × 10–8 m–1 for the factor f, found by minimizing the vertical angle discrepancies in the 1990/91 dataset. Combining optical and GPS observations is not straightforward. Vertical and horizontal angles measured by a theodolite are naturally referenced to a local curvilinear coordinate system that is tied to the local geoid, whereas GPS positions are more naturally referenced to a geocentric Cartesian coordinate system that is independent of the Earth’s gravitational field. In order to simultaneously analyze data of both types, we first transformed all optical data into the GPS geocentric Cartesian coordinate system, approximating the direction of gravity by the normal to the World Geodetic System 1984 (WGS84) ellipsoid. Further details can be found in the Appendix.
The simultaneous reduction of survey observations involves minimizing the observation discrepancies weighted by their standard errors (see Equation (A2)). The standard errors determine the relative importance of each observation in forming the combined solution. Using a standard error that was too small on a particular (possibly erroneous) observation would yield a solution overly influenced by that observation. In practice, we used observation standard error values that were larger than typical bench-measured instrument precisions, since, in addition to instrumental imprecision, the standard errors must accommodate errors associated with markers that wobble and settle in compacting firn, as well as undetected observer errors. A single standard error was assigned to each of the optical observation types: 7 arcsec for horizontal angles, 20 arcsec for vertical angles and 25 mm for EDM ranges. GPSurvey software reports standard deviations for individual baseline solutions as part of its output. To balance the GPS observation discrepancies with those of the optical observations in the simultaneous solution, we uniformly scaled the reported standard deviations so their horizontal and vertical components had medians of 13 and 133 mm, respectively.
The resulting velocities and expected errors (see Equation (A17)) for markers in the core-site subregion of the Taylor Dome network are shown in Figure 3a. These were obtained by combining all GPS and optical observations collected over six successive field seasons. The errors are very small relative to the velocities; the error ellipses are barely visible over most of the grid. Those markers with trajectories constrained by GPS observations (this includes most markers except those with × > 22 km) have comparatively smaller parameter error estimates for two reasons. First, the GPS data show higher precision over long baselines than the optical survey data. Second, these markers were observed over a longer time-span, thus reducing the signal-to-noise ratio for their trajectory parameters. To a good approximation, the flow direction follows the surface slope. Ice velocities in the surveyed region are generally <1 m a–1, except on the south slope where accumulation rate is high and the ice flows into a deep subglacial channel. The strainrate pattern in Figure 3b shows, predominantly, extension in the direction of flow, and relatively minor strain rates transverse to the flow. This means we can assume plane strain when modelling the flow, particularly between the divide and the core site.
Fig. 3. Surface ice motion in the region of the core (see box in Fig. 2) with 10m surface elevation contours. The star marks the core site and the heavy solid line is the path of the ground-based radar profile used to define the domain for the ice-flow model. Surface and bed topography closely resemble those along the flowline shown by the dashed transect. (a) Ice velocity from a combination of GPS and optical survey data. Velocity uncertainties are indicated by ellipses at the downstream end of the velocity vectors. A 1 m a–1 scale bar with a 10% error ellipse is shown. (b) The strain rates calculated from the velocity field shown in (a). A scale bar for a strain rate of 3 × 10–4 a–1 is shown. Outward arrows indicate extension.
Ice-Flow Modelling
The measured surface velocity field can be used both to identify flowlines for plane-strain modelling and to constrain the calculated velocity. The ice-core site at Taylor Dome is 3 km south of the flow divide. Ice in the top of the core was deposited at the core site;ice deeper in the core originated closer to the divide. Since the cross-flow divergence along the flowline between the flow divide and the core site is small (see Fig. 3b), the flow can be treated as approximately two dimensional. Reference Waddington, Morse, Grootes, Steig and PeltierWaddington and others (1993) used the two-dimensional, plane-strain, flow model developed by Reference RaymondRaymond (1983) to predict the ice-core depth–age scale at Taylor Dome prior to drilling the core. Here we improve on this earlier ice-flow model by using higher-resolution profiles of surface and bed topography (Reference MorseMorse, 1997), measured accumulation rates (Reference MorseMorse and others, 1999) and finer grid resolution. The modelling presented here was also used to support the analyses of Reference Morse, Waddington and SteigMorse and others (1998) and Reference SteigSteig and others (2000), although few details were presented in those papers.
The surface and bed topography measured along the path of the (approximately) flow-parallel radar profile shown by the solid curve in Figure 3 define the model domain. The radar transect was diverted by several hundred meters to avoid radar interference from the core site (star in Fig. 3). As a result, the profile does not closely follow the ice-flow direction 2 km downstream from the core site. However, because lateral gradients in surface and bedrock slope are small near the core site, that offset section closely approximates the geometry along the dotted transect. The radar dataset can also represent the flowline through that dotted section, which also passes close to the core site. We discretize the cross-section using increased vertical node density with depth to accommodate strain-rate gradients near the bed, and increased horizontal node density, where necessary, to resolve steep bed topography and associated velocity gradients (Fig. 4a). The bed profile was smoothed to avoid node-to-node roughness in the velocity fields, and the overall ice thickness from radar measurements was reduced by 22m to account for the firn column density being less than that of ice (i.e. the model is in ‘ice equivalent’ thickness units). The model puts the surface topographic crest and the flow divide at ψ = 19km (Fig. 4), consistent with the ice motion measurements. The modelled cross-section extends more than 15 km in each direction from the divide, to reduce the influence that inexact boundary conditions at the ends of the model domain might exert on the flow solution near the core site.
Fig. 4. (a) Finite-element mesh used to model ice flow in vertical section through the core site at ξ = 21 km. Measured along the path in Figure 3, this section extends from ξ = 3 km (coinciding with the right margin of Fig. 3) to ξ = 32 km (corresponding to the left margin of Fig. 3). The upper boundary is the best match to the measured surface topography in the vicinity of the ice core, following the adjustment procedure described in the text. (b) Ice equivalent accumulation rate used for model calculations, derived from the depth to a shallow, continuous radar reflector calibrated by gross β-radioactivity measurements. (c) Comparison of measured (+) and calculated (solid curve) horizontal component of surface flow along the profile. (d) Calculated particle trajectories that intersect the ice core (indicated by the vertical line) at 50 m depth intervals.
The model uses a Glen-type, isotropic, non-linear flow law of the form
where 
ij
is strain rate, τij
is deviatoric stress, and its second tensor invariant, τ, is the effective stress. We adopt the value 3 for the exponent n, and 4.9 × 10–25 s–1 Pa–3 (at–10°C) for the softness parameter A which has an Arrhenius temperature dependence and an activation energy of 60 kJ mol–1(Reference PatersonPaterson, 1994). E is a scalar enhancement constant that can be adjusted to account for other factors influencing the stiffness of the ice. We treat E as uniform over the model domain, although it should depend on spatially varying ice properties.
The temperature field at Taylor Dome is only weakly coupled to ice flow because of the low accumulation rate and associated slow rate of ice flow. This is evident in the measured borehole temperature profile that varies nearly linearly with depth (Reference Clow and WaddingtonClow and Waddington, 1996; Reference MorseMorse, 1997). We estimate the temperature field along the modelled profile by extrapolating the measured surface temperature downward with the same depth gradient as that observed in the borehole. This simple assumption gives temperatures that fall within 2°C of the three-dimensional finite-difference temperature modelling results of Reference MorseMorse (1997).
We apply a combination of velocity and stress boundary conditions. The ice base is frozen to the bed and its velocity is assumed to be zero. The upper surface has zero traction. On the lateral boundaries, following Reference ReehReeh (1998), we specify the horizontal component of velocity by a profile obtained from an integration of the surface-parallel strain rate over depth, applying a temperature-dependent softness parameter A. This approach is sometimes termed the ‘shallow-ice approximation’. The horizontal velocity at these boundaries is scaled so the outward flux balances the integrated upstream accumulation rate. The spatial pattern of accumulation rate shown in Figure 4b was derived from the depth of a continuous, shallow radar layer calibrated to β-radioactivity accumulation rate measurements (Reference MorseMorse and others, 1999). The finite-element model calculates an internal velocity field and the upper, free surface is allowed to evolve until the surface topography and flow reach a steady state in balance with the prescribed accumulation rate.
We use the flow-law rate enhancement parameter E as a convenient, non-dimensional model ‘tuning’ parameter. Our lateral boundary conditions prevent a change in average ice thickness in the computational domain. Therefore, for a given accumulation rate, softer ice produces an ice sheet with lower surface slopes, since less stress is needed to drive the required mass flux. Using a value of 5 for E made the modelled steady-state surface geometry match the measured surface elevation profile as closely as possible in the region between the flow divide and the core site, while also matching the measured surface velocity field (Fig. 4c). Although values of E >1 are typical to account for dustladen, hence soft, glacial ice in Greenland (e.g. Reference Hvidberg, Dahl-Jensen and WaddingtonHvidberg and others, 1997), the value E = 5 for Taylor Dome ice probably accounts for an enhanced rate of surface-parallel shear deformation due to the moderately developed, vertically aligned c-axis ice fabric observed in the ice core by L. Wilen (personal communication, 1998). A scalar E cannot also represent the increased stiffness for vertical thinning and longitudinal extension associated with a vertically aligned anisotropic c-axis fabric. However, at more than one ice thickness from the divide, the shear deformation is dominant.
We expect that the modelled velocity and strain-rate patterns are good representations of the flow leading to the ice-core site. Since the surface fit was biased toward matching the topography in the divide region, including the core site, the solution represents flow conditions farther from the divide less accurately. For example, north of the divide (to the right in Fig. 3a) the radar transect diverges from the flowline, and near ξ = 27 km (x = 10, y = 19 km in Fig. 3), ice flows over a sharp bedrock pinnacle. The model requires a more pronounced surface undulation over this feature than is observed. This discrepancy arises from the plane-strain restriction of the model;the actual flow probably goes around as well as over the pinnacle. However, these limitations have little impact on the calculated flow to the core site.
Modelling Results
We can now use the modelled flow field to augment paleoclimate interpretations of the ice-core data. Using a thinning function, as described below, measured thicknesses of layer packets of known temporal duration can provide estimates of past accumulation rates after the expected thinning due to ice flow has been taken into account. However, spatial gradients in accumulation rate can complicate this analysis. Therefore, an ultimate goal is to separate known spatial patterns of accumulation from temporal accumulation rate changes that represent changing climate. Our goal here is to infer the accumulation rate history at the locus of origin points of particle paths that end in the ice core today, because this history relates geochemical tracer concentrations in the core to fluxes from the atmosphere.
Spatial gradient in accumulation rate
Field measurements (e.g. Fig. 4b; see also Reference MorseMorse and others, 1999) show that the modern accumulation rate is approximately 20% greater at the core site (ξ = 21 km) than at the divide (ξ = 19 km). This pattern is controlled by the surface topography;the core site is on the upslope side of the dome for modern moisture-bearing storm trajectories (Reference MorseMorse and others, 1999). From the southward dip of internal layers, Reference Morse, Waddington and SteigMorse and others (1998) concluded that this pattern (of higher accumulation to the south) persisted over most of the Holocene, but was reversed during the Last Glacial Maximum (LGM).
If the flow divide has been stable, then ice recovered in the core travelled along the paths shown in Figure 4d. Ice at progressively greater depths in the core originated from surface sites progressively closer to the divide, where today the accumulation rate is less than at the core site. Figure 5a shows the scaling factor that relates the accumulation rate at the deposition site to the contemporaneous accumulation rate at the ice-core site. The scaling is derived by mapping the relative accumulation rate at the surface onto the ice core, following the particle paths in Figure 4d. This relationship becomes uncertain below approximately 330 m, i.e. prior to establishment of the modern (Holocene) gradient. At earlier times when the accumulation rate gradient was reversed, the scaling factor could exceed unity. Future work to infer regional Holocene climate change from Taylor Dome core properties must take into account this 10–15% spatial variation in accumulation rate associated with ice-source location. For analysis of the record prior to the LGM, the ice-source location is very close to the divide and rescaling to account for the spatial gradient is unnecessary.
Fig. 5. (a) Accumulation rate at site of deposition, relative to contemporaneous accumulation rate at the core site, for ice recovered at depth in the core. The gray region indicates uncertainty in relationship over the 325–450m depth interval corresponding to the period of reversed accumulation rate gradient (Reference Morse, Waddington and SteigMorse and others, 1998). (b) Thinning function, Λ(z), gives layer thickness relative to thickness at time of deposition, as a function of depth in the Taylor Dome ice core.
Thinning due to ice flow
Since ice is incompressible, horizontal extensional flow at divides is accommodated by vertical thinning of layers. With increasing depth, the ice has undergone successively greater total vertical compressive strain, and any climatic record that may be recorded in the ice column becomes vertically compressed. Using the modelled velocity field, we calculate the depth profile of total vertical strain experienced by ice within the core by tracking the total vertical shortening of small ice volumes as they move along the particle trajectories that lead to the core site. This gives the relative layer thickness curve, or thinning function, Λ(ξc, z), shown in Figure 5b for the ice-core site at ξ = ξc . In steady state, the thickness of an annual layer at depth z at a core site ξc is the product of Λ(ξc, z) and the accumulation rate at the origin point ξ0(ξc, z) of the particle trajectory that intersects the core at ξ c and depth z:
An ice-core depth–age relation can then be calculated by integrating annual-layer thicknesses from the surface to depth z in the core,
The dashed curve in Figure 6 gives the ice-core depth–age relation resulting from temporally constant accumulation rate, spatially distributed as shown in Figure 4b, and steady ice flow that follows the trajectories in Figure 4d.
Fig. 6. Depth–age scales for the Taylor Dome ice core. Age control points were established from: (1) correlation of the δ 18O profile with the Vostok (East Antarctica) δD profile (Reference Grootes, Steig, Stuiver, Waddington, Morse and NadeauGrootes and others, 2001); (2) correlation of bubble gas profiles with the GISP2 ice core (Reference SteigSteig and others, 1998; Reference Brook, Harder, Severinghaus, Steig and SucherBrook and others, 2000); and (3) the depth of two prominent 10Be concentration peaks recognized in the GISP2 and Vostok cores (Reference SteigSteig, 1996). If we assume that the modern spatial patterns of ice flow and accumulation rate have been steady through time, we calculate a depth–age scale (dashed curve) that diverges from the observed ages below 350 m. When those steady spatial patterns of flow and accumulation rate are scaled through time by the accumulation rate history shown in Figure 7b, we calculate a depth–age profile (solid curve) that fits the observed ages.
An improved Taylor Dome accumulation rate history
An accumulation rate history can be inferred from the depth-age relation of an ice core, when corrections can be made for the amount of thinning experienced by layers at each depth due to ice flow. Accumulation histories have been previously derived for Taylor Dome (Reference Morse, Waddington and SteigMorse and others, 1998; Reference SteigSteig and others, 2000) using this approach. Here we update those results using the improved ice-core depth–age scale of Reference Grootes, Steig, Stuiver, Waddington, Morse and NadeauGrootes and others (2001) that was obtained by correlating the stable-isotope record with that of the Vostok (East Antarctica) ice core. This depth–age scale is consistent with earlier Taylor Dome depth–age scales of Reference Brook, Harder, Severinghaus, Steig and SucherBrook and others (2000) from occluded gas concentrations correlated with the annual-layer-counted GISP2 ice core, and of Steig and others (1998, 2000) from combined stable-isotope, gas-concentration and 10Be measurements. However, the Reference Grootes, Steig, Stuiver, Waddington, Morse and NadeauGrootes and others (2001) depth–age scale provides greater temporal resolution. Control points for each of these determinations are compared with the steady-state model prediction in Figure 6.
The discrepancy between the modelled and observed depth–age scales (Fig. 6) below 350 m leads us to reconsider the assumptions of the model. Several factors not included in the physics of the flow model, such as evolving ice c-axis fabric, and time-varying basal or lateral boundary conditions, could have influenced the flow at the core site. However, temporal variations of the accumulation rate have the most direct bearing on the vertical velocity at or near an ice divide. Reference MorseMorse (1997) showed that the spatial pattern of ice flow at Taylor Dome has been stable for at least the last 104 years. Reference MorseMorse (1997) also concluded that the thickness and slope of Taylor Dome during the last glaciation were similar to today because the tendency for the ice sheet to thin in response to the lower accumulation rate was counteracted by its tendency to thicken due to colder, and therefore more viscous, ice. Characteristic response times are τ d = H/ḃ for dynamic thickness changes and τ th = H 2/κ for thermal changes, where H ≈ 550 m is a characteristic ice thickness, ḃ ≈ 0.05 m a–1 is a characteristic accumulation rate and κ ≈ 10–6m2s–1 is a characteristic thermal diffusivity. Because these times are both of the same order as the time required for major climate changes (10 kyr), ice-sheet response should not lag climate change significantly. In addition, the underlying high topography has a stabilizing influence on the divide position. It is therefore reasonable to assume that Taylor Dome was always close to steady state, in balance with its changing climate conditions (accumulation rate and temperature). Furthermore, because the topography did not change, the spatial pattern of flow did not change and ice continued to move along the modern streamlines at speeds that varied with the temporal changes in accumulation rate and ice temperature. The thinning profile, Λ(ξ, z), is determined by the spatial pattern of ice flow; in the following analysis we assume that Λ(ξ, z) is independent of the magnitude of the ice-velocity field. If the accumulation rate varied through time, but in such a way that the ice-sheet surface and the particle paths were unaffected, then the annual-layer thicknesses today are given by
where the accumulation rate at the deposition site, ξ 0, can vary with time. This expression and Equation (3) can be used to calculate an accumulation rate history consistent with an independently determined depth–age scale (e.g. using dates derived by correlating geochemical signatures with those in a well-dated ice core). We constructed a trial function of accumulation rate as a function of depth, converted it to a function of age using the known depth–age scale, then evaluated the depth–age scale it implied through Equation (3), and compared that depth–age scale to the known ages. Iterating, we adjusted the accumulation history until an acceptable fit was obtained with the known ages. Earlier versions of accumulation rate histories inferred by this procedure were given in Reference Morse, Waddington and SteigMorse and others (1998) and Reference SteigSteig and others (2000) based on the depth–age estimates available at the time. We now use the updated depth–age determinations of Reference Grootes, Steig, Stuiver, Waddington, Morse and NadeauGrootes and others (2001) to improve on the earlier accumulation history estimates. Choosing a piecewise-constant form to be compatible with the Reference Grootes, Steig, Stuiver, Waddington, Morse and NadeauGrootes and others (2001) method of identifying age correlation points at climate transitions, we compute the accumulation rate history (shown as the bold line in Fig. 7b) that produces the depth–age scale shown by the solid curve in Figure 6. This history has not been re-scaled with the spatial gradient of accumulation presented in the earlier section. It represents conditions at the time-varying site of snow deposition, rather than at a fixed point in space, so it is directly comparable with geochemical records from the core.
Fig. 7. (a) Oxygen isotope profile from the Taylor Dome ice core indicating major climatic events over the past 150 kyr, adapted from Reference Grootes, Steig, Stuiver, Waddington, Morse and NadeauGrootes and others (2001). The thick solid curve in (b) is the piecewise-constant accumulation rate history that is consistent with a combination of the Reference Grootes, Steig, Stuiver, Waddington, Morse and NadeauGrootes and others (2001) age determinations and the modelled ice dynamics at the site. We compare our accumulation rates with histories derived from the concentrations of 10Be (crosses) and SO4 (thin solid line) following the methodology of Reference SteigSteig and others (2000). We used dry-deposition fluxes of 1.2 × 109atoms m–2 a–1 and 2.9 × 10–6 kgm–2a–1, respectively. Wet deposition is negligible at this site. Differences between the two methods at 15–30 kyr BP and around 50 kyr BP may reflect postdepositional loss of snow by wind scouring.
The accumulation rate history shows a strong correlation with the climate inferred from the δ 18O profile (Fig. 7a); warmer periods are generally associated with higher accumulation. The departure from this trend before approximately 100 kyr BP may result from decreasing applicability of the thinning function modelled for a steady-state ice-sheet geometry in the lowest 10% of the ice column, although age determination errors may also contribute. Notable are the very low modelled accumulation rate values for the LGM period (approximately 15–30 kyr BP) and around 50 kyr BP, which corresponds with a ‘warm’ interval inferred from the δ 18O record.
When a geochemical tracer is deposited onto the ice sheet at a uniform rate (i.e. constant flux) it is diluted by snowfall, so its measured concentration in the ice yields an estimate of snow accumulation rate. Figure 7b includes two additional estimates of snow accumulation, each based on tracer dilution and thus each independent of the modelled accumulation rate history. (However, they follow similar deposition pathways, so they may not be independent of each other.) First, Reference SteigSteig and others (2000) inferred an accumulation rate history from the concentration of 10Be in the ice core;we reproduce that record in Figure 7b. Second, we derived an accumulation rate history from the concentration of non-sea-salt sulfate. The latter is justified by measurements on the Vostok ice core by Reference Legrand and DelmasLegrand (1995), which suggest that variations in atmospheric loading (and hence deposition rate) of non-sea-salt sulfate are small over the glacial-interglacial transition, while Reference SteigSteig and others (2000) showed that concentrations of 10Be and non-sea-salt sulfate tracked each other closely at Taylor Dome. The general agreement of these three accumulation rate histories gives support for the modelled history. Notably, both the 10Be- and SO4-derived profiles show higher snow accumulation values than the modelled result during the LGM and 50 kyr BP periods. The species concentration is comparatively low, considering such low snow-deposition rates and assuming constant deposition flux for these species. We suggest that this signature is indicative of post-depositional wind scouring, which removed the trace species along with a fraction of the surface snow. In effect, the geochemical tracers record the total precipitation from the atmosphere, while the ice-dynamics method infers the net accumulation, after wind has blown away some of the deposited snow. The ratio of the two independent estimates allows the fraction lost to be estimated. Figure 7b suggests that wind scouring may still be active, but the fraction of snow removed has been much smaller in the Holocene than at the LGM.
Conclusions
Measurements of surface topography and ice motion are essential for constraining ice-flow model calculations which, in turn, provide information about ice flow at depth. Inferring the ice motion at the surface from a suite of observations is not always straightforward. When various parts of the network must be surveyed over extended and possibly nonoverlapping time periods, reduction-to-epoch methods cannot always be applied. Here we use a least-squares minimization procedure to simultaneously determine marker positions and velocities from an overdetermined set of survey observations. Using a geocentric coordinate system permits assimilation of both optical and GPS observations. Robust solution of the minimization is obtained by singular value decomposition of the matrix relating observations to marker positions and velocities.
Ice-flow modelling at Taylor Dome is simplified by its near-planar configuration in the vicinity of the core site, and by its relatively weak thermomechanical coupling. Using our numerical ice-flow model, we identify streamlines and the associated source locations for ice at depth in the core. Based on other considerations (see Reference MorseMorse, 1997) we treat these streamlines as invariant. By accounting for the total strain experienced by ice at depth in the ice core, we calculate an accumulation rate history from the thickness of datable layer packets in the ice core whose time-span is known from geochemical analyses. This is the accumulation history at the point of origin on the surface for ice at each depth. Although these origin points change through time, the accumulation record we obtain is directly comparable to geochemical climate proxies in the ice core, which originated along the same path over the ice-sheet surface through time. Because this accumulation rate history is independent of geochemical tracer concentrations, it can be used to evaluate tracer deposition-rate assumptions and/or post-depositional snowerosion effects.
Acknowledgements
We thank H. Conway, T. Gades, R. Hawley and all those who helped us to acquire the field data. We are grateful to R. Frolich for sharing ideas and experience with ice-motion surveys at the British Antarctic Survey and to M. Truffer and an anonymous referee for careful reviews of the manuscript. Antarctic Support Associates provided field logistical support and the University Navstar Consortium (UNAVCO) provided GPS support. This research was supported by grants OPP-8619265, 8915924, 9221261, 9421644 and 0636997 from the US National Science Foundation.
Appendix Survey Analysis with Moving Markers
Problem description
A geodetic survey measures geometric relationships between selected markers in three-dimensional space. In practice, these measurements usually involve the relative positions of reference markers (e.g. optical survey targets and reflecting prisms) and instruments (e.g. theodolites and GPS antennas), each positioned at a known height above a site. The measurements may be: the horizontal angle formed by two markers and an instrument;the difference in zenith angle between a marker and an instrument, or the distance between them;any of the three coordinates of an instrument, or differences in any of the coordinates between two instruments. The first three are typical of optical surveying, and the last two are typical of satellite surveying (GPS). We use poles as markers for our survey sites so they are observable from a distance. It is specifically the locations of intersection of the poles with the snow surface that are the site coordinates that we seek. In the analysis there is no distinction between markers and instruments;in the following we refer to them collectively as markers.
A well-constrained survey includes redundancy (i.e. multiple measurements of markers) to reduce the uncertainty in the overall result. Often ice velocity determination is the objective, so surveys of identifiable markers are performed over time. The essence of our method to simultaneously analyze such datasets is the estimation of trajectories of the markers such that calculated geometric quantities (distances, angles, etc.) derived from positions along those trajectories agree as closely as possible in a weighted least-squares sense with field measurements of those quantities.
We assume that each marker moves at constant speed along a straight path according to six trajectory parameters 
= (X, Y, Z) and 
= (U, V, W), in which (X, Y, Z) are its initial position coordinates and (U, V, W) are its velocity components. The position of a marker at time t is
where T is the time when it is at . In general, the reference time can differ from marker to marker, but to simplify the formulation we assign the same T to each of them. The method could easily be extended to nine trajectory parameters by incorporating accelerations in each of the three directions, but Equation (A1) is adequate for small t – T in typical ice-sheet settings.
Solution procedure
For N pts markers (‘pts’ to indicate surveyed ‘points’), some of the 6 × N pts trajectory parameters might be specified, such as a known position for a stationary marker. The remaining N adj free parameters are determined as the solution of a nonlinear least-squares minimization problem, having as its data N obs > N adj measurements of the geometric quantities relating the markers. The quantity to be minimized is the root-mean-square discrepancy R given by
in which 
is the measured quantity, and σ
1 is the estimated standard error in . The corresponding quantity QI
is calculated from the trajectory parameters Pm
of the markers involved in the measurement. The problem is linearized by first writing the measurement discrepancy in the form
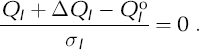
The increment ΔQI is the amount QI would change if the N adj parameters Pm were changed by ΔPm . A first-order Taylor series expansion yields
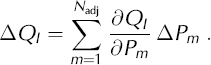
Here Pm is any of the parameters X, Y, ...,W for any location, and ΔPm is any of ΔX,ΔY,...,ΔW. When Equation (A4) is substituted into Equation (A3), it can be rearranged as
which expresses how discrepancies can be reduced or eliminated by suitable changes ΔPm in the parameters. There are N obs equations of the form of Equation (A5), for l = 1,..., N obs. These equations make up an overdetermined system of linear equations
in which: (1) row I of the N
obs × N
adj matrix A contains the derivatives ∂QI
/∂Pm
scaled by σ
l; (2) the N
adj elements of vector 
are adjustments ΔPI
to the adjustable parameters ; and (3) the weighted measurement discrepancy ( – QI
)/¤I
is element I of the vector 
which has N
obs elements. The type of the measurement (angle, distance, etc.) determines how QI
is expressed in terms of the trajectory parameters.
To form the traditional normal equations for a least-squares solution, the lefthand side of Equation (A5) would be substituted into the righthand side of Equation (A2), then the partial derivative of R 2 with respect to changes ΔPm in each parameter Pm would be set to zero. A standard least-squares solution X can be found by solving the N adj normal equations in N adj unknowns. However, the solution of the normal equations requires finding the inverse of matrix ATA, which can be singular or near-singular. Instead of forming the normal equations, we solve the overdetermined system of equations (A6) directly, using the SVD method (e.g. Reference Press, Flannery, Teukolsky and VetterlingPress and others, 1986, p. 59) to find a pseudo-inverse for matrix A. (In our case, we used the SQRLSS routine, which is part of the US National Institute of Standards and Technology Core Math Library (CMLIB).) When a stable solution to the normal equations exists, the SVD approach yields the same least-squares solution. When the normal equations yield a near-singular matrix ATA, SVD can still produce the best solution in a strict least-squares minimization sense.
Using SVD, the non-square matrix A can be written as a product of three other matrices,
where the columns of the N obs × N obs matrix U are orthonormal vectors spanning the data space, and the columns of the N adj × N adj matrix V are orthonormal vectors spanning the parameter space. The N obs × N adj matrix W is zero everywhere except along the diagonal of the upper N adj rows. These non-negative elements wnn arranged in decreasing magnitude along the diagonal, are called the singular values, which are also the square roots of the eigenvalues of ATA. The pseudo-inverse of A, which we will call B, is given by
The N adj × N obs matrix Ŵ is also non-zero only on the diagonal of its first N adj columns. The nth diagonal element is 1/wnn where wnn is the corresponding singular value in matrix W. When the ratio of the smallest to largest singular values approaches machine precision, the smallest singular values wnn produce large and meaningless values for 1/wnn in Ŵ. SVD algorithms such as SQRLSS routinely replace large values of 1/wnn by zero to eliminate problems caused by near-singularity and machine round-off.
In general, the N obs standard errors σI differ from observation to observation, and they remain as irreducible factors in the normal equations formed from Equation (A2). While σI appears only as a weighting factor on the Ith equation in the system of equations (A6), nevertheless the relative weights on those N obs equations do matter in over-determined systems. If σI is increased, the weight given to the I th equation (and therefore to the I th observation) in Equation (A6) is diminished in the SVD least-squares solution.
Because the elements of matrix A and vector depend on , as will be detailed below, the system of equations (A6) cannot be solved in a single pass. The adjustable parameters that minimize R
2 are found by iteration.
Formulation of measurement types
Although the minimization is found in terms of adjustable parameters, , the QI
are more easily expressed in terms of the coordinates (xi
, yi
, zi
) of the markers at the time of their measurement. Application of the chain rule gives the partial derivatives of the QI
with respect to the trajectory parameters to form the ∂QI/∂Pm
term in Equation (A6).
Coordinate and coordinate-difference measurements
The calculated coordinates of an instrument at site i are 
where 
relates the instrument location to the marker location, (xi
, yi
, zi
), and is assumed to be known exactly. Differentiation with respect to the site coordinates gives 
which, in terms of the underlying trajectory parameters, becomes
The row of matrix A corresponding to this measurement contains six non-zero elements 1/σI for the three components of 
and (t – T)/σI
for the three components of 
.
Similarly, a coordinate difference between markers at sites i and j at time t, for example the difference in the y coordinate δyji = yi – yi, becomes
Distance measurements
The distance between a marker at site j and another at site i is the length of the coordinate-difference vector 
between them:
When differentiated this gives, in terms of site coordinates,
In terms of trajectory parameters we apply Equation (A9) to ∆xi and other coordinate adjustments.
Vertical angle measurements
A vertical angle ϕji
is measured from the local zenith at site i to the marker at site j. Rearranging the expression for the scalar product of the unit zenith vector 
and the coordinate-difference vector gives the cosine of the angle between them
The f term corrects for the Earth’s curvature and for atmospheric refraction (e.g. Moffitt and Bouchard, 1982). A straightforward chain rule application gives the differential of ϕji with respect to the underlying site i and j trajectory parameters.
Horizontal angle measurements
For markers at sites i and k observed from site j, projections of the coordinate-difference vectors
and
onto the local horizontal plane are given by
and
The horizontal angle θjki observed by a theodolite is the angle between these two vectors. Their scalar and vector products yield two expressions for θjki
and
which are readily differentiated to express ∆θjki in terms of the underlying trajectory parameters. Details can be found in Morse (1997).
Error estimates
An advantage of our formulation for simultaneously determining all trajectory parameters is that it minimizes the aggregate of all the discrepancies;in so doing, the solution also explicitly takes into account the estimated error in each measurement. An estimate of trajectory parameter errors can be obtained directly from the measurement uncertainties σI. Equation (A6) can be rewritten as
where matrix B is the pseudo-inverse of A. With B so constructed, its elements approximate the derivatives ∂PI/∂dm of trajectory parameter PI with respect to measurement m. The covariance between trajectory parameters Pi and Pj is given by
Here, the i, j element of the N
adj × N
adj matrix C is the covariance cov(Pi
, Pi
) of trajectory parameters Pi
and Pi, and the K, L element of the N
obs × N
obs matrix D is the covariance cov(dK
, dL
) of the discrepancies associated with measurements K and L. Because the discrepancies are scaled by the uncertainties of the measurements, the elements of are dimensionless samples from distributions with zero mean and unit variance, i.e. 
. As a consequence, cov(dK
, dL
) will be normalized also;that is, it will be numerically equal to the correlation (–1 to 1) between discrepancies dK
and dL. If the measurement errors are uncorrelated, D becomes the identity matrix, and Equation (A16) reduces to
In this case, the diagonal elements of C are the squares of the expected parameter errors.
It is worth checking whether the discrepancies (defined by the righthand side of Equation (A5)) that are produced by a solution are consistent with the a priori standard deviations σl
. For example, when the expected errors for each observation are normally distributed, and if the observations are uncorrelated, then each normalized discrepancy is a sample drawn from a distribution with zero mean and unit variance. For sample sizes larger than 101 to 102, the expected value of a sum of squares of random samples approaches the number of samples (Parker, 1994, p. 124). Equivalently, R
2 in Equation (A2) should approach unity. If R
2 > 1, the a priori measurement uncertainties σI
have been underestimated. If R
2 is smaller than unity, either σI
have been overestimated, or the solution overfits the data, i.e. significant errors exist in the solution .
If the measurement uncertainties σI
have been checked and found to be appropriate, SVD provides a way to select a solution that produces the most reasonable match to the data. Each singular value (diagonal element wnn
) is associated with the nth column of V, which is an orthonormal basis vector in the model space. When the singular value wnn
is small, that particular linear combination of parameters has little influence on predictions of the data. As a result, 
is not well constrained; a wide range of parameter solutions, including a wide range of large multiples of , is possible without significantly worsening the fit to the data as expressed through R
2 in Equation (A2). By setting 1/wnn
= 0 in Ŵ, that particular poorly constrained linear combination of parameters represented by is eliminated from the parameter solution. This can produce a parameter solution with reduced variances C (Equation (A16) or (A17)), while increasing R
2 by only a small amount. By successively eliminating the smallest singular value until R
2 = O(1), the best least-squares solution that is consistent with the data uncertainties can be obtained. Our solutions for the Taylor Dome dataset produced R
2 of order unity using the default number of retained singular values from SQRLSS. This indicates that the original measurement uncertainties were estimated well, and that the parameter solution is reasonable.
Coordinate systems
A coordinate system must be chosen in which to form the trajectory solutions. A complication arises for theodolite measurements, since they measure the angles projected onto horizontal and vertical planes as determined by local gravity, thus requiring knowledge of the gravity vector in the chosen coordinate system. For surveys that utilize theodolite measurements and are less than ~10km in spatial extent, it is common to construct a locally defined Cartesian space in which the vertical coordinate axis is parallel to the gravity vector at every point. An Earth-curvature correction that increases quadratically with horizontal distance must then be applied to vertical angles (e.g. Moffitt and Bouchard, 1982). Such a coordinate system is in a sense conformal, in that great circle paths map to straight lines with constant ‘z’ coordinate. Errors introduced from distortion of the coordinate system are spread over the network.
We use a geocentric Cartesian coordinate system for the Taylor Dome survey. Incorporation of the GPS-derived observations in this system is straightforward: GPS-measured positions are explicitly coordinate-type observations, and baselines from differential surveys are triplets of coordinate-difference measurements. Since the geoid is poorly known in Antarctica, particularly adjacent to the Transantarctic Mountains, we approximate the direction of gravity by the normal to the WGS84 ellipsoid. This approximation is justified since errors introduced from uncertainties in the gravity vector primarily affect the vertical angle measurements which themselves are of poor reliability due to varying atmospheric refraction effects.
