Introduction
The physical properties of snow are extremely variable and snow strength shows this variability to a marked degree. The strength of snow is a function of many parameters, among which are density, texture, and thermodynamic history. These parameters are variable across both space and time. It appears not to be possible to quantify the variables adequately enough to permit the prediction of strengths of specific bodies of snow in Nature. Thus, the variability of snow strength becomes an inherent property which must be dealt with.
Statistical strength theories
Statistical analyses are methods of dealing with variability. There are two major classes of statistical strength theories: series-element theories and parallel-element theories. The series-element theories are also called weakest-link theories by analogy with the failure of a chain.
Series-element theories
The formulation of this class of theories involves two basic assumptions:
(1) There is a distribution of strengths within the material, and
(2) Failure of one element of the material precipitates failure of the entire body, as the failure of a weak link causes the failure of a chain.
The most widely quoted series-element theory is that of Weibull (1939[a],[b]) where he also proposed a unique cumulative distribution function:
where V is the volume, σ is the failure stress, σu, σo, and m are distribution constants. The Weibull distribution given above is the three-parameter distribution which includes the truncation stress σu below which the probability of failure is zero. Some sort of truncated distribution is undoubtedly more realistic than one which would have a finite probability of zero strength.
Weibull’s formulation of the series-element theory is incomplete for real materials. The median failure stress given by Equation (1) increases without limit as the volume decreases to zero. As an example, Reference SommerfeldSommerfeld (1974) presents Weibull constants derived from centrifugal tensile tests on snow. Using his layer 5, with a density of 230 kg m₋3, a volume of 10₋5 m3 would give a median failure stress of about 30 - 105 N m₋2or about twice the mean strength of pure ice. This physically absurd result indicates that Weibull’s distribution is not realistic below a certain volume range. Weibull comments on this problem (1939[b]). He points out that distribution functions for real materials should probably be truncated at both upper and lower stresses. For the types of material which he considers, he justifies the assumption that the upper limit can be approximated by infinity and concludes that this is an adequate approximation for all but extremely small volumes. As shown above, such an approximation is unrealistic even for appreciable volumes of snow.
It is generally recognized that the physical basis behind Weibull’s and other statistical strength theories is the existence of flaws which weaken the material (Reference EpsteinEpstein, 1948). Weibull’s assumption that there is no upper limit on the strength is essentially the assumption that an unflawed element of the material has infinite strength. Thus, elements which are so small they do not include a flaw would, under Weibull’s theory, contribute unrealistically high strengths to a body. One method of handling this problem would be to limit the minimum volume for which the Weibull distribution can be used, and Weibull’s discussion implies such a limit. While a limit does not truncate the strength distribution at the high end, it would limit the mean strength which would be calculated. Conceptually, such a limit would be equivalent to limiting the volumes of the elements to volumes which would include at least one flaw per element. The difficulty of detecting and evaluating flaws in snow limits the usefulness of this concept, but we will see later that there is some experimental evidence on the size of flaws in snow. Reference ColemanColeman (1958) argues that the requirement that the elements are statistically independent implies a lower bound on the volume for which this type of analysis is valid.
Other formulations of weakest-link theories have been made. These are concisely reviewed by Reference EpsteinEpstein (1948). As he points out, however, material strength data are usually not accurate enough to make a rational decision among various distributions used for these different formulations from the data alone. This comment is especially true of the measurements of snow strength.
Parallel-element theories
Parallel-element theories are well represented by Daniels’ (1945) classic work. The formulation of parallel-element theories involves two basic assumptions: (1) There is a distribution of strengths within the material, and (2) Elements act independently without failure propagation between elements, A consequence of the latter assumption is that there is no catastrophic failure mechanism. Failure of one element does not ensure failure of the entire body; the failure simply transfers that element’s share of the load to the remaining elements. The Daniels strength, the failure stress of an entire collection of elements (a bundle), is found from the relationship,

where στ is the stress at failure. Reference DanielsDaniels (1945) does not build his theory around any particular distribution function: the theory is general enough to use any density function f(σ) including Reference WeibullWeibull’s (1939).
Application to snow
The two types of strength theory represent two extreme ideas of the failure mechanisms of materials with variable strength. Both types predict that the mean strength of a number of samples should decrease as the number of elements in each sample increases. For very large specimens each theory predicts very small variability in measured strengths. However, the large-volume strength predicted by Reference WeibullWeibull’s (1939) theory is, in general, significantly lower than that predicted by Daniels’ (1945) theory. As pointed out by Reference EpsteinEpstein (1948), real materials can be expected to exhibit behavior which is some combination of the two types of theory.
Reference Kinosita [i.e. Kinoshita] and OuraKinosita (1967) showed that snow exhibits different properties in compression tests depending on the rate at which the stress is applied. Below a certain stress rate, depending on the temperature, snow compresses without fracture. Above that rate snow normally fractures in a short period of time. The stress which snow can sustain in compression at low stress rates is greater than it can sustain at high stress rates. Reference PerlaPerla (1977) also presented some data indicating that shear-frame tests performed at slower rates give higher strengths than those performed at higher rates.
For high stress rates Weibull’s model should be more realistic than Daniels’ model. At high stress rates, the stress concentrations would not have time to relax and could lead to catastrophic failure. At lower stress rates, such relaxation should be possible, and Daniels’ model should be more realistic. Furthermore, Weibull’s model should apply better to tension experiments, where the sides of the cracks which form do not remain in contact and cannot re-sinter. In shear expdriments the crack sides do remain in contact and Daniels’ model should be better.
Using a Weibull distribution in the Daniels relationship results in a model of a material with combined properties as discussed above. Different Weibull distribution shapes are obtained by using different volumes in Equation (1). Thus a family of Daniels strengths can be obtained from a particular set of Weibull parameters by choosing different volumes for the individual elements. For example, if we are trying to predict the strength of a large volume, say 1 m3, we would calculate a wide range of values depending on the volume chosen for the Daniels elements. If we chose 1 m3 as the element volume we would have a one-element Daniels body with a strength equal to the weakest flaw. This is a degenerate case where the Daniels body is identical to the Weibull body and would give the lowest strength of the family of strengths mentioned above. On the other extreme is a body made of elements of such a volume that each contains one flaw, as discussed previously. I hypothesize that this volume is the lower limit on the Weibull distribution as applied to real materials. Using this volume would result in the highest in the family of strengths one would obtain from the Daniels relationship, given a particular set of Weibull parameters and the hypothesized volume limitation. I would further hypothesize that snow would exhabit this strength at very low stress rates.
At very low stress rates the failure of one flaw should not propagate throughout the sample or through a portion of the sample. It would merely cause a transfer of its share of the load to all the surviving flaws. However, if each volume element of the model contained more than one flaw, the failure of one flaw would remove the other flaws in that model volume element from supporting the load. This concept may be clarified somewhat by considering a mechanical model to simulate the material. A combination Weibull—Daniels body could be a number of chains of equal length, connected in parallel, perpendicularly between two stiff parallel bars. Suppose each chain contained six links, which would he analogous to six flaws per element. When a link failed, six links would no longer bear the load: the link which failed and the five other links in the chain. However, a basic assumption for a pure Daniels material is that the failure of one link transfers the load to all the remaining links. Thus the basic assumption would only be fulfilled if each element contained only one link, or by analogy, one flaw per volume element. This type of problem has also been discussed in Reference GublerGubler (1978) from a different viewpoint.
Analyses of experimental data
Accurate data on snow strength are still scarce. Strength tests on snow are difficult to perform. The difficulty of working with snow as a material, and the rigorous conditions under which tests are performed limit accuracy. While available data are insufficient to test the above speculations definitively, they do provide some support. Furthermore, an analysis of available data will show where further experiments are needed.
Reference SommerfeldSommerfeld and King (1979) presented shear-frame data on avalanche sliding layers. Stress rates leading to avalanches are very low. Reference SommerfeldSommerfeld and King (1979) showed that the Daniels strength calculated from shear-frame measurements predicted the failure stress at low stress rates very well (Table I).
TABLE I. A comparison of Daniels strengths and failure Stresses of Seven Avalanches.

If Daniels’ second assumption, that the elements act independently, holds for snow shear- frame tests, the data of Reference SommerfeldSommerfeld and King (1979) can be analyzed in a simple way to predict the size effect. For example, 0.03 m2 samples could be created by combining the original 0.01 m2 samples, three at a time. Daniels gives the method of calculating the strengths of such combinations in his section on small bundles (see also Reference EpsteinEpstein, 1948).
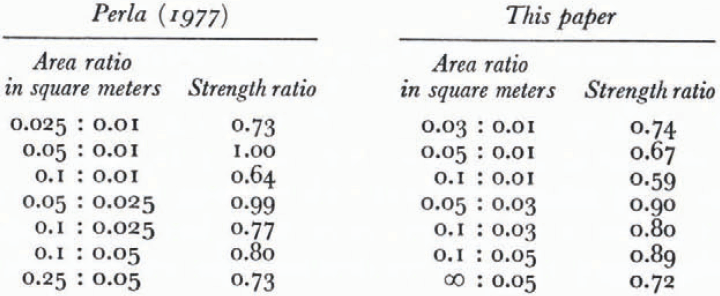
The results for such combined samples are compared with Reference PerlaPerla’s (1977) data on the size effect in shear-frame tests in Table II. It is seen that, except for the comparison between 0.01 and 0.05 m2 the agreement is satisfactory. Of particular interest are the larger size comparaisons. Daniels’ theory predicts a decrease in variability with increasing size, which Perla found. This also means that Perla’s data for the larger sizes should be more accurate. The discrepancy at 0.01-0.05 m2 can probably be explained by the large variability in Perla’s measurements with the smaller frames. More data are necessary for a definitive test of the applicability of Daniels’ statistics to snow shear-frame tests. However the data which are available support such an application and indicate that Daniels’ second assumption is realistic for snow in shear at least within the accuracy of the data.
TABLE II. COMPARISON OF EXPERIMENTAL DATA ON THE SIZE EFFECT IN SHEAR-FRAME TESTS WITH CALCULATIONS PROPOSED IN THIS PAPER
McClung (unpublished) presented some data on larger-volume tensile tests. His results for dry, equi-temperature, metamorphosed snow are shown in Figure 1 Also shown is the line fitted to the minimum Weibull strengths σu, calculated for similar types of snow (Reference SommerfeldSommerfeld, 1974). It is clear that σu forms a lower envelope to McClung’s data. Also shown in Fig. 1 is a line for the Weibull failure stress of McClung’s volumes calculated with Reference SommerfeldSommerfeld’s (1974) Weibull constants. Again the Weibull strengths are too low to explain McClung’s data.

Fig. 1 Reference McClungMcClung’s (1974) data compared with different statistical strength analyses using Sommerfeld’s (1974) Weibull constants.
McClung’s tests were at low stress rates. He proved he was working in the “ductile range” by introducing serious stress concentrators in some of his specimens without much effect. It would be expected that at low stress rates, snow would exhibit some measure of Daniels behavior.
The average Daniels strengths shown in Figure 1 were calculated using Reference SommerfeldSommerfeld (1974) Weibull constants, assuming V = 5 - 10 ₋4 m3. It fits McClung’s (unpublished) data as well as can be expected considering the scatter. There is some experimental evidence that 5 - 10 ₋4 m3 is about the right size for a lower limit on V in Equation (1). Reference Keeler and WeeksKeeler and Weeks (1967), Reference KeelerKeeler (1969), and Reference MartinelliMartinelli (1971) all reported zero strengths in some of their measurements using volumes of 5-10₋4 m3, indicating that their samplers were interfering with flaws. Reference SommerfeldSommerfeld (1974) obtained no zero strengths with samples of 2.3-10₋3m3.
Conclusions
Applying statistical strength theories to snow results in quantitative explanations of many of the features of snow strength testing. Failure of snow in large volumes at low stress rates can be predicted from tests on small volumes at high stress rates. In the case of shear-frame tests, the elements act independently and thus exhibit almost pure Daniels behavior, with very little Weibull behavior. Tensile tests appear to exhibit a mixture of the two types of behavior. A problem with the tensile tests is that the appropriate volume for use in the Weibull distribution is uncertain. A comparison between Reference SommerfeldSommerfeld’s (1974) and McClung’s (unpublished) results indicates that it should be about 5 - 10₋4 m3. This agrees with the results of Reference Keeler and WeeksKeeler and Weeks (1967), Reference KeelerKeeler (1969), and Reference MartinelliMartinelli (1971) as discussed above.
It is possible to propose a model of snow-slab failure, based on these conclusions. At the slow loading rates which occur on the usual avalanche slope, the snow should behave in a manner modeled better by Daniels. However, if ductile cracks begin to form, they become stress concentrators, and more importantly, stress-rate concentrators. If the stress-rate concentrators increase the stress rate into the more brittle range, the snow flips over into Weibull behavior and exhibits a lower strength. Since the stress on the snow is at the Daniels strength, the change to Weibull behavior, with its lower strength, precipitates catastrophic failure.
A small amount of evidence exists in favor of this model. McClung (unpublished) proved he was in the “ductile” range by introducing serious stress concentrators in his samples with little effect. However, his samples fractured, indicating that at some point in the test the stress rate became high enough to cause brittle fracture. Another piece of data which bears on this point comes from strain measurements which I made during a natural avalanche release (Reference SommerfeldSommerfeld, 1979). The strain-rate measured across a three meter distance was 1.08 - 10₋7 s₋1. This strain-rate is more than an order of magnitude too low to cause tensile fracture (personal communication from R. L. Brown; unpublished data of H. Singh). Therefore, the strain-rate must have been concentrated at some point in the snow-pack.
A final point is unrelated to the above speculations. Reference PerlaPerla (1969) states that the high ratios of mean tensile strength to mean shear strength obtained by previous workers could not be “reconciled with the standard theory of strength of materials which predicts σ⁄τ ≤ 2”. McClung’s large-volume tensile strengths average about 1.5 - 10₋3 N m₋2 and the largevolume shear strengths of Reference SommerfeldSommerfeld and King (1979) averaged about the same. Largervolume tensile tests would average somewhat lower, easily satisfying the above inequality. Perhaps the high ratios previously found were an artifact of the small sample size and the statistics of snow strength.




