1. Introduction
In the European Alps, the retreat of glaciers is now a familiar picture. It is also a clear signature of climate change (Reference ChurchChurch and others, 2001). While glacier fronts in various Alpine regions fluctuated in the course of the 20th century, they mostly retreated while temperature mostly rose (Reference Böhm, Auer, Brunetti, Maugeri and NanniBöhm and others, 2001). Glacier shrinkage has been particularly strong in the last 20 years as global and alpine temperatures have peaked to levels unprecedented in the past century. Glacier fluctuations and current glacier retreat affect the local as well as global, natural as well as societal environment: changing water and tourist resources, glacier-related risks, etc. Understanding the recent changes, in order to evaluate whether they are likely to amplify and by how much in the future, requires that the sensitivity of glacier mass balance to climate is well understood and quantified.
Glacier surface mass balance (SMB) has often been modeled only using the most accessible meteorological data: air temperature and precipitation (e.g. degree-day models). More sophisticated models exist (Reference Klok and OerlemansKlok and Oerlemans, 2002), but few of them have been used to simulate glaciers over decades or more while resolving small-scale spatial features. Rather, over long periods of time, glaciers are generally modeled as bulk, and distributed mass balance is ignored. Accurate testing of the sensitivity of glacier mass balance requires the development and use of physically based and spatially distributed models. A physically based model is desirable to limit ad hoc adjustments based on present-day measurements and to capture processes that determine sensitivity. Spatial distribution at glacier subscales is needed to separately and adequately resolve accumulation and ablation and account for different contributions to sensitivity to climate change.
In the present paper, a distributed physically based snow/ice mass- and energy-balance model is applied to two test glaciers in the French Alps, calibrated and validated. Our model is developed based on the snow model Crocus (Reference Brun, Martin, Simon, Gendre and Coléou.Brun and others, 1989, Reference Brun, David, Sudul and Brunot1992) and responds to a full range of surface meteorological parameters (2 m air temperature, 10m wind speed, 2 m air relative moisture, precipitation quantity and phase, incoming direct and diffuse solar radiation, incoming longwave radiation, and cloudiness). Test glaciers are glaciers for which SMB monitoring has been comparatively intensive for both spatial and seasonal aspects and over a number of years. No meteorological observations are available on or next to the glaciers, so instead we use synthetic data that combine disaggregated large-scale meteorological analysis and nearby observations. These are provided by the SAFRAN model (Reference Durand, Brun, Mérindol, Guyomarc’h, Lesaffre and MartinDurand and others, 1993) for the period 1981–2004. Once validated, the mass-balance model can be used to test SMB sensitivity to the various input meteorological parameters. Sensitivity results are further extended using a generic demonstration glacier, the physical characteristics of which are simplified to be free of local influence (mountain shadow, avalanche accumulation or snow redeposition).
2. Test Glaciers (Saint-Sorlin and Argentière), Glaciological and Meteorological Data
2.1. The test glaciers
The longest and densest existing observational dataset of glacier SMB in the French Alps pertains to Glacier de Saint- Sorlin, located in the Grandes Rousses range (45°10′N, 6°10′E) (Reference VincentVincent, 2002; Fig. 1). This is a relatively small glacier (3 km2), with a north- to northeast-facing slope and an altitude range of 2650–3400 m. Direct observations of the SMB on Glacier de Saint-Sorlin have been performed since 1957 (Reference Vincent, Vallon, Reynaud and Le Meur.Vincent and others, 2000; Fig. 2). Since 1994, accumulation and ablation have been separately measured on a seasonal basis: measurements are made on all parts of the glacier at least twice a year, in spring (at the end of the accumulation season) and in fall (at the time of the first persistent snowfall). Additional (~monthly) measurements are usually performed during the ablation season.

Fig. 1. Maps of Glacier de Saint-Sorlin and Glacier d’Argentière, with their locations in the French Alps (triangles). For each glacier map, the space between two coordinates (Lambert) is 1 km.

Fig. 2. Cumulative specific net balance for Glacier de Saint-Sorlin and Glacier d’Argentière (adapted from Reference VincentVincent, 2002). Solid line is a degree-day model reconstruction. Small triangles are spatially averaged field measurements; large triangles are from old maps and photogrammetry.
Glacier d’Argentière, located in the Mont Blanc area (45°55′N, 6°57′E) (Reference VincentVincent, 2002; Fig. 1), is another relatively well-monitored glacier in the French Alps, with a surface area of 13 km2 and an altitude range of 1600–3600 m. It is a valley glacier mainly oriented northeast, but with emissary glaciers oriented south (Améthystes) to north (Rognons). Its mass balance has been monitored since 1975 (Fig. 2) with the same method as for Glacier de Saint-Sorlin, but the density of observations is smaller because of its greater extent.
Maps of the the two glaciers and other additional data can be found at http://www-lgge.ujf-grenoble.fr/ServiceObs/index.htm. The characteristics of the two glaciers differ, offering complementary validation potential for mass- balance models.
2.2. Glaciological measurements and errors
In spring, winter accumulation is evaluated by coring (about 20 drill sites for Glacier de Saint-Sorlin) from the surface down to the previous summer snow, which can be identified as transformed, dirty and ice-layered, or to the ice in the net ablation zone. A density profile is performed along the core to convert snow depth into water equivalent. Stakes are inserted in the boreholes to monitor the summer ablation of snow. In addition, in the net ablation zone, stakes are inserted in the ice using a steam probe in order to monitor the summer ice ablation. For Glacier de Saint-Sorlin, there are currently about 30 measurement sites distributed on the whole glacier, and the ablation zone (where the largest changes have been observed in the past) is more extensively monitored. The combination of these two types of measurements gives the annual mass balance at the end of the ablation season.
Detailed evaluation of the errors in these field measurements is needed, and is provided here since it seldom appears in the literature. Our evaluation of measurement errors is based on extensive field experience gained on Saint-Sorlin, Argentière and other glaciers monitored by Laboratoire de Glaciologie et Géophysique de l’Environnement, Grenoble. Similar errors may be expected in work done by others elsewhere who use similar methods. The main errors are summarized in Table 1. Although seldom explicitly referred to in the following, the data in Table 1 have been used throughout the full model adjustment and validation process. An example is provided in Figure 3 which shows how model and observations generally agree within the estimated error bars on observations. The sources of errors used to evaluate the content of Table 1 are synthetically presented below for others to use and adapt as necessary and appropriate:

Fig. 3. Yearly winter accumulation and annual mass balance as measured and modeled on Glacier de Saint-Sorlin at 2780 m. Large patterned bars are field measurements with their error bars (Table 1); thin white bars are corresponding Crocus simulations for the same period (winter or year).
Table 1. Uncertainties in field measurements of SMB, in cm w.e. See text for details

-
1. An uneven surface induces uncertainty in stake readings and drilling depth;
-
2. An uneven borehole bottom also results in inaccurate drilling depth evaluation;
-
3. For winter mass-balance measurement, some of the bottom part of a core can remain in the borehole and falsify drill depth measurements;
-
4. In the accumulation area, determining the transition between two years in a core on the basis of snow color and structure can be somewhat approximate when fall frost crusts are present in snow. On the other hand, such transition in the ablation zone is accurately identified as an ice/snow interface;
-
5. Measuring the size and weight of snow core samples in the field to evaluate density and thus water equivalent involves errors;
-
6. Because drilling is labor-intensive, the depth of snow accumulated since the previous summer is sometimes, in the ablation zone, simply evaluated using a snow probe. This is clearly less accurate than drilling a core;
-
7. Summer ablation can reach several meters, so stakes longer than 2m are both impractical to use and susceptible to breakage when emerging too high above the surface. Instead, 10m stake trains composed of 2 m stakes attached to each other by either a metal chain (stronger;in the ablation region) or string (in the accumulation region) are used. When one of the 2m elements fully emerges from the surface, it simply falls aside. However, the link between two stakes cannot be made perfectly tight, and this induces reading errors that accumulate with the number of fallen stakes;
-
8. The ice horizon that marks the end of the summer season in the ablation zone can be unequivocally used to measure winter accumulation. On the other hand, since the start of the accumulation season cannot be predicted, underestimation of the annual mass balance is possible in the accumulation zone if significant melting occurs after the last reading of summer ablation stakes and before the first persistent winter snowfall;
-
9. Internal accumulation in the accumulation area (Reference Lliboutry and EchevinLliboutry and Echevin, 1975), i.e. refreezing in the snowpack of surface melted snow, affects stake readings but is not in principle a source of errors here because this is also taken into account in our model.
Altogether, errors in SMB determinations from fieldwork are significantly higher in the accumulation area (up to 0.40 mw.e. in annual balance) than in the ablation zone (up to 0.15 mw.e. in annual balance) (Table 1). However, these are local errors for each single measurement. They can be sign-biased but are otherwise random and thus decrease when spatially and/or temporally averaged. In addition to field measurement uncertainties, when adjusting or validating the model using a constant digital elevation model, variations of the real surface altitude of the glacier throughout the simulation period (up to 20 m over 1981–2004) affect comparison with observations. When converted to mass-balance errors using an altitudinal mass-balance gradient of 0.008 m w.e. m–1, they can reach 0.16 m w.e.
Geodetic measurements of the glaciers using photogrammetry are occasionally performed at the end of the summer and provide alternate and independent quantitative information on glacier SMB (section 3.3). The rms error is estimated to be 0.5–1 mw.e. on average over the glacier, depending on photographic resolution. Geodetic measurements are used to monitor overall volumetric changes over several years and verify that they are consistent with the continuously monitored or model SMB variations. Also, using ancient maps and aerial photographs, it is possible to reconstruct the mass balance of the glaciers before the SMB was monitored in the field (Reference Vincent, Vallon, Reynaud and Le Meur.Vincent and others, 2000). Figure 2 shows the observed cumulative mass balance of the two glaciers since the early 20th century using field data, photogrammetry and maps, along with the degree-day model results of Reference VincentVincent (2002). This figure shows that the last 20 years of the 20th century, the main validation period in the present paper, are a period of particularly fast shrinkage of the two glaciers.
In addition to the mass balance, ice flow on the two glaciers is monitored. This information is not used, because we are concerned here with the SMB, but the flow can affect the temporal significance of SMB measurements since the stakes move in the course of a year and from year to year. However, the lifetime of stakes is such that, with ice velocities of a few tens of meters per year at most (Reference Vincent, Vallon, Reynaud and Le Meur.Vincent and others, 2000), they need to be replaced before they move across distances larger than the horizontal resolution of our model (200 m).
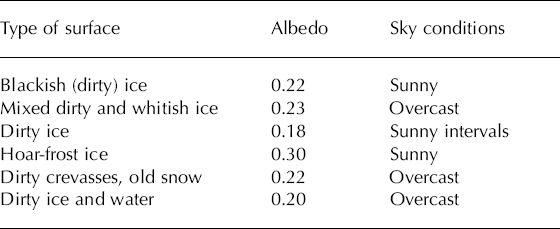
The albedo of various ice surface types (flat ice, rough ice, crevasses, ice with variable amounts of rock remains and dust deposits) in the ablation zone was measured in July 2003. The results are reported in Table 2 and range from <0.20 up to 0.30. Such low values are not exceptional, and Reference Strasser, Corripio, Pellicciotti, Burlando, Brock and FunkStrasser and others (2004) report albedos of 0.1–0.2 on Haut Glacier d’Arolla, Switzerland, depending on the morainic charge of ice surface. The relevant surface characteristics are complex and variable, as reported by Reference Brock, Willis and SharpBrock and others (2000), and our model cannot objectively account for these. Rather, the observations in Table 2 are averaged to prescribe a uniform albedo of ice in the model as described in section 3.1.
Table 2. Mean albedo measurement over ice at Glacier de Saint- Sorlin, depending on type of surface, in July 2003. Each type of surface was measured on several spots; for each spot, the albedo is averaged over 5 min of measurement
2.3. Meteorological data
The SMB model we used is based on the snow model Crocus (section 3.1) which runs with the following hourly meteorological parameters in input: 2 m air temperature, 10m wind speed, 2m air relative moisture, precipitation quantity and phase, incoming surface direct and diffuse solar radiation, incoming surface longwave radiation, and cloudiness. None of these parameters is presently observed on or in the vicinity of glaciers in the French Alps, although such observations are planned in the future on Glacier de Saint- Sorlin and Glacier d’Argentière. However, the SAFRAN analysis tool, a meteorological disaggregator of the larger- scale meteorological information (Reference Durand, Brun, Mérindol, Guyomarc’h, Lesaffre and MartinDurand and others, 1993), provides all the meteorological parameters needed for Crocus, separately for the various mountain ranges in France (each range is <1000 km2), depending on slope exposure (north, east, southeast, south, southwest, west, flat) and altitude (in 300m steps). SAFRAN assimilates large- scale fields from meteorological analysis and local information from automatic weather stations and manual measurements at ski resorts. The SAFRAN/Crocus system was initially developed by Météo-France for operational avalanche risk evaluation and forecasting.
For the present work, the SAFRAN analysis is available for the full 1981–2004 period (1981–2003 on Glacier d’Argentière). With this meteorological dataset, it is possible to evaluate an SMB model over >20 years through a period during which glacier evolution in the Alps has been particularly marked (Fig. 2). Operational snow modeling and avalanche forecasting in the last decade have demonstrated that the SAFRAN/Crocus system reproduces well both the intra-seasonal and interannual variability of the seasonal snowpack in the Alps (Reference Brun, David, Sudul and BrunotBrun and others, 1992). However, in such an application, the snowpack is periodically reinitialized, once a year before the first autumn snowfall, and neither the performance of Crocus nor that of SAFRAN is well verified in summer when seasonal snow has melted. For glacier modeling, reinitialization is neither possible nor required, and summer is a critical time during which most of the ablation occurs. Moreover, SAFRAN may have some limitations for our application: there are fewer field observations in the mountains during summer, and there is no observation at the glacier altitude, especially for a parameter such as precipitation. At the high elevation of glaciers, local valley effects are less important and the large- scale analysis in input to SAFRAN should exert more control on SAFRAN output than for the lower elevation. On the other hand, glaciers tend to create their own atmospheric conditions close to the surface (section 3.1) and this is not explicitly taken into account. Thus, in spite of a strong operational snow modeling heritage, careful validation of the SAFRAN/Crocus system for glacier modeling is necessary before it is used for sensitivity analysis.
3. Surface Mass-Balance Modeling
3.1. Crocus: from snow to glacier modeling
The Crocus model (Reference Brun, Martin, Simon, Gendre and Coléou.Brun and others, 1989, Reference Brun, David, Sudul and Brunot1992) was initially developed to simulate Alpine seasonal snow and assist in avalanche risk evaluation. It is currently in operational use at Météo-France to issue avalanche risk bulletins in the Alps and other mountain regions. Crocus has also been applied to various uses outside its originally planned domain of application, for example to simulate Antarctic (Reference Dang, Genthon and MartinDang and others, 1997) and Greenland snow (Reference Genthon, Fily and MartinGenthon and others, 2001). It is a one-dimensional multi-layer physical model of the snow cover, which explicitly evaluates at hourly steps the surface mass and energy budgets, including turbulent heat and moisture surface exchange with the atmosphere and outgoing radiation, and the internal disposal of mass and energy. There are 50 subsurface layers taken parallel to the slope surface, through which mass and energy are exchanged to account for physical processes such as heat diffusion, radiation transfer or liquid-water percolation. Phase changes are taken into account and snow densification and metamorphism are parameterized, affecting mass and energy transfer and changing the surface albedo.
Although Crocus is initially a snow model, it can be adapted to account for glaciers by considering ice in the model as a particular kind of snow with density, heat and liquid-water capacity and conductivity, radiative properties, and surface roughness of ice. A major difference between snow and glacier ice at the surface is albedo and thus the absorption of radiation. While snow albedo can be very high (>0.9) when fresh, the albedo of an ice surface is much lower (as low as 0.20 or even less;section 2.2), not only because the ice is intrinsically darker, but also because the surface is generally rougher and dirtier (e.g. rock remains, dust deposits) when ice is exposed. In Crocus, the surface albedo is separately defined in three spectral bands. For snow, it is calculated according to grain-size and shape and age (Reference Brun, David, Sudul and BrunotBrun and others, 1992). No modification has been done here. For ice, it is prescribed as 0.23 in the 0.3–0.8mm band, 0.15 in the 0.8–1.5mm band and 0.06 in the 1.5–2.8 mm band, based on observations reported in section 2.2. No dependence on solar angle is presently taken into account, nor on cloudiness as suggested by Reference Jonsell, Hock and HolmgrenJonsell and others (2003).
When ice is exposed at the surface, the turbulent fluxes calculated by Crocus are increased due to the higher roughness of ice and the exposure of rocks and crevasses to correctly model the melt. The roughness length is then prescribed as z0 = 2 mm, which is within the wide range of values found in the literature (Reference Greuell and SmeetsGreuell and Smeets, 2001; Reference Greuell, Genthon, Bamber and PayneGreuell and Genthon, 2003), instead of the original z 0 = 0.3 mm for snow. Ablation is thus well reproduced.
Finally, the basal energy flux has been modified. When Crocus runs for seasonal snow, i.e. not for a glacier, the heat accumulated in the soil during the summer snow-free season must be released at the snowpack base during winter. This is not the case for glaciers, where the bedrock is not exposed. The geothermal heat flux at the bed–ice interface is weak and does not affect the surface: the bulk of the ice is not a significant source or sink of heat since the glaciers we study are temperate, i.e. much of the ice remains close to 0°C. Thus, a no-flux condition is applied at the base of our simulated snow/ice slab, which is simply initialized at 0°C with sufficient thickness (200 m) to insure that only a fraction can be melted over the length of the simulations.
During summer, because its surface temperature cannot exceed 0°C, a glacier creates its ‘own’ surface atmospheric layer that differs from the meteorological conditions external to the glacier: surface temperature inversion, depressed diurnal temperature variations, katabatic winds, etc. (Reference Greuell and Böhm.Greuell and Bohm, 1998; Reference Strasser, Corripio, Pellicciotti, Burlando, Brock and FunkStrasser and others, 2004). Tentatively adapting Crocus so that turbulent fluxes account for this effect, using Reference Greuell and Böhm.Greuell and Bohm’s (1998) glacier wind parameterization on Glacier de Saint-Sorlin with parameters originally derived from Pasterzenkees, Austrian Alps, leads to a relative warming of the air above the glacier compared to SAFRAN temperature, instead of the expected cooling. Indeed, Reference Strasser, Corripio, Pellicciotti, Burlando, Brock and FunkStrasser and others (2004) show that the adjustment parameters of such a transfer function vary with glacier characteristics, but no observation is available to carry out such an adjustment on glaciers in the French Alps. The glacier impact on summer surface meteorology is thus ignored here, a possible source of error. However, the fact that summer ablation appears to be reasonably reproduced without any direct adjustment suggests that this is not a major model shortcoming.
3.2. Spatially distributed mass-balance modeling
Here, the Crocus model is run on a 200 m resolution grid extending over the full surface of the glaciers. It was verified that finer grids do not bring significant improvement because only aspects that are not taken into account by the model (e.g. avalanche accumulation, crevasses) could significantly benefit from higher resolution. At each grid- point, topographical parameters (altitude, slope, orientation) are determined from a digital elevation model. This is used to linearly interpolate the SAFRAN meteorological input (available for different altitude and exposition each hour) in elevation and orientation and to prescribe snow accumulation and adequate solar angles and exposure throughout the day. Impacts of surrounding rises are taken into account for solar radiation (topographic shading) but not for longwave radiation (radiation emitted by surrounding snow or rock faces is not taken into account).
All simulations start on 1 August 1981, the start date of the available SAFRAN data. A glacier is initialized as bare ice at all gridpoints. Once the winter season is reached, snow accumulates and a realistic snowpack quickly builds up. Observations and degree-day modeling (Reference Vincent, Vallon, Reynaud and Le Meur.Vincent and others, 2000) indicate that the glaciers are still in approximate equilibrium in 1981, before a period of rapid shrinking later on. Therefore, the influence of partly unrealistic initial conditions is likely to vanish soon after simulations start, although the first few months may be significantly affected. All simulations are carried out over the full period for which the SAFRAN data are available, here August 1981 to July 2004 (2003 for Glacier d’Argentière). There is no observation-based reinitialization of the snow/ice profiles in the course of a simulation.
It is found that using SAFRAN data without adaptation yields an underestimated winter accumulation. This is because SAFRAN provides precipitation for a range of orientation and elevation but does not account well for the precipitation enhancement effects which are due to topography (valley channeling of the atmospheric flow, gravity- driven accumulation, etc.). In addition, because the variability of precipitation is observed to be large, even at the scale of a mountain range, the fact that SAFRAN precipitation needs to be corrected at the scales and subscales of a glacier is not unexpected. However, precipitation is the only adjusted parameter in the meteorological input to Crocus. All other data from SAFRAN are used without correction. The precipitation adjustment is made to reproduce the observed spatial distribution of winter accumulation using ad hoc distributed multiplication factors. Multiplication factors are determined independently at 31 (Glacier de Saint-Sorlin) and 20 (Glacier d’Argentière) control sites where winter mass-balance observations provide sufficient control over several years. The multiplication factor is about 1.5 in most places, resulting in a reasonable reconstruction by Crocus of both summer and winter mass balance (Fig. 3). It is somewhat larger at the foot of steep slopes and lower in areas much exposed to wind. Although an altitude dependence of precipitation is already parameterized in SAFRAN (Reference Durand, Brun, Mérindol, Guyomarc’h, Lesaffre and MartinDurand and others, 1993), it appears to be insufficient for glaciers. This may be because SAFRAN precipitation is poorly constrained at these altitudes (section 3.3), or possibly because topography is more marked in the vicinity of glaciers than on average. Avalanches and wind transport can also contribute to higher accumulation on glaciers than elsewhere at similar elevation. After adjustment on control sites, the precipitation factor distribution is interpolated over the whole model grid, and full-scale simulations are carried out. Snapshot and long-term mean spatial distributions of the calculated SMB can then be obtained (Figs 4 and 5).

Fig. 4. Cumulative specific net balance on Glacier de Saint-Sorlin and Glacier d’Argentière for the period 1981 to 2004 (2003 for Argentière). The solid line is the model mass balance for Glacier de Saint-Sorlin; the dashed line is the model mass balance for Glacier d’Argentière. The large triangles are the geodetic reconstructions. For Glacier de Saint-Sorlin, small triangles are measured specific mass balance (averaged with Reference LliboutryLliboutry’s (1974) linear model), and small crosses are mass-balance reconstruction using a degree-day model (Reference VincentVincent, 2002; winter accumulations are calculated on 1 June, and summer ablations on 1 October).

Fig. 5. Model mean annual mass balance for Glacier de Saint-Sorlin and Glacier d’Argentière, 1981–2003. The thick line is the equilibrium line. Mass balance is expressed in mw.e.
3.3. Validation and comparison with other SMB reconstructions
One way to validate the simulated SMB is to use only part of the available field observations to adjust the precipitation factor distribution, then use the other part to check the model results. However, even on Glacier de Saint-Sorlin and Glacier d’Argentière, the available winter SMB observations provide a barely sufficient control against which precipitation can be adjusted. This is because, although observations are frequent compared to other glaciers, we use many control points to adequately capture the spatial distribution of precipitation at model grid resolution. Moreover, the mass balance is intensively measured only since 1994. On the other hand, field measurements of summer and annual mass balance are available for independent validation, once winter accumulation is adjusted by the precipitation factors. The result of such a validation is shown in Figure 3 for one altitude on Glacier de Saint-Sorlin. The model mass balance is in reasonable, though not systematic, agreement with the measurements within the error bars of observations (section 2.2;Table 1), and there is no systematic bias.
There are other independent indicators of the variability of the SMB that may be used to verify model results. In particular, because spatially distributed simulations are produced, it is possible to determine the position of the snowline at any time and to compare with observation. In summer, the snowline delineates the region where the winter snow has not (yet) melted. At the end of the ablation season, the snowline is the equilibrium line that separates the accumulation and ablation zones. It can be identified from ground or aerial photographs, or from satellite imagery. Such data are not used to run or adjust the model, and thus provide an independent method of model validation. For the model, the snowline is calculated as the zero-balance line, with mass balance calculated since the first persistent snowfall of the previous winter. This has been compared with satellite images (Système Probatoire pour l’Observation de la Terre (SPOT); Landsat;Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER)) over the period 1984–2002 (Reference Gerbaux, Dedieu, Etchevers and VincentGerbaux and others, 2004). Satellite images were selected for dates when annual snowlines can be seen (no freshly deposited snow). An example is displayed in Figure 6 which shows that the broad position of the snowline is realistic in the model. Figure 7 shows that the interannual variations of the model and satellite-derived mean altitude of the snowline correlate quite well (r2 = 0.94). Thus, years with particularly high or low ablation are well reproduced, with only one exception, 1992, for which the modeled accumulation appears to be underestimated. We have no explanation yet for this deficiency.

Fig. 6. Comparison of the snowline position between satellite imagery (© Spot-Image) (left) and Crocus model (right) for 30 September 1997 on Glacier de Saint-Sorlin. The mass balance is expressed in m w.e. and is calculated since the beginning of the previous winter in the model.

Fig. 7. Mean model vs satellite-derived altitude of the snowline on Glacier de Saint-Sorlin for various dates in the period 1985–2002.
Another way to check the model mass balance is to use geodetic reconstructions of the glacier topography which provide volumetric changes of the glacier. This can be done using stereo photographs and, for the more remote past, old topographic maps which, if integrated over the full glacier to be free of the influence of ice flow, provide an integrated SMB change from the previous topographic reconstruction (Reference Vincent, Vallon, Reynaud and Le Meur.Vincent and others, 2000). To minimize uncertainties associated with the variable density of snow, photographs are generally taken when the snow cover is minimal, i.e. at the end of the summer ablation period. On Glacier de Saint- Sorlin, there are five, and on Glacier d’Argentière three, geodetic reconstructions available for the 1981–2004 period. Figure 4 shows that the model results coincide well with the geodetic reconstructions.
The SAFRAN/Crocus results, degree-days results and measured specific mass balance (using Reference LliboutryLliboutry’s (1974) linear model) agree with each other as to the general trend in the evolution of Glacier de Saint-Sorlin SMB through 1981–2004 (Fig. 4), but some discrepancies can be identified. SAFRAN/Crocus appears to overestimate the SMB, but it is in better agreement with geodetic reconstructions than degree- day results or spatially averaged mass balance, particularly before 1993, possibly because there were fewer field observations then. It should be kept in mind that because cumulative SMBs are shown here, any error for one particular year will propagate through time until errors of opposite sign compensate. All sources of information appear to be in fairly good agreement in the latest part of the record. Strong melt is well reproduced during the extremely hot summer of 2003.
In summary, Crocus with SAFRAN data as meteorological input successfully reproduces most aspects of the mass balance of the test glaciers as known from observations. Ignoring the possible glacier control on surface meteorology, and having relatively limited information to set albedo or roughness characteristics of ice (section 3.1) thus appear to have relatively minor consequences for model capabilities.
3.4. Discussion of model results
Although largely determined by elevation, the spatial distribution of the SMB on the glaciers (Fig. 5) is also affected by slope exposure. For instance, an ablation area on the slope facing east between Col des Quirlies and Pic de l’Etendard on Glacier de Saint-Sorlin is reproduced, although accumulation dominates at similar and higher elevations elsewhere, with more northern surface orientation. Obviously, a model that only takes into account the altitudinal component of the mass balance cannot reproduce such patterns. For Glacier de Saint-Sorlin, the mean SMB ranges from ~–2.5 m w.e. a–1 (ablation) at the snout to ~1 m w.e. a–1 (accumulation) in the higher parts, in good agreement with the observations where available. On Glacier d’Argentière, a mean net ablation of ~11 mw.e. a–1 at the glacier snout is probably an overestimation since the model does not account for the glacier being partly rock-covered there. The mean accumulation reaches 2 mw.e. a–1 on the highest part of the emissaries, a result which is probably reasonable but cannot be accurately verified with available field data. For the period 1981–2004, the mean ELA is 3005 m on Glacier de Saint-Sorlin. According to Reference Vincent, Kappenberger, Valla, Bauder, Funk and Le Meur.Vincent and others (2004), the mean ELA was ~100m lower on average in the 1957–97 period. This is consistent with the last 23 years being a period of accelerated glacier shrinking (Fig. 2).
In fact, model results indicate that Glacier de Saint-Sorlin has lost ~19m of water (averaged over the full glacier) between 1981 and 2004, i.e. ~0.83ma–1 on average (Fig. 4), while over 1957–97 the mean mass loss was only 0.31 mw.e.a–1 (Reference Vincent, Vallon, Reynaud and Le Meur.Vincent and others, 2000). According to SAFRAN data, this melting increase in the last 22 years can primarily be associated with a mean temperature increase of 1.3°C over the period 1981–2003 at 2600–3100 m altitude. For the same period, snowfall increased by 7% at 3000 m and decreased by 2% at 2700 m. The role of precipitation in the mass-balance trend is thus negligible.
Glacier d’Argentière has lost on average 12 mw.e. from 1981 to 2003, or about 40% less than Saint-Sorlin. There are seven years of positive mass balance in the period, compared to four for Saint-Sorlin. One reason for the weaker SMB change on Glacier d’Argentière is that the temperature increase through 1981–2003 is weaker for this glacier (0.7°C). Another probable reason is that the surface of the accumulation area, relative to the ablation area, is wider on Glacier d’Argentière. Because of the albedo feedback when the surface changes from snow to ice in the melting season, the SMB is less sensitive to climate change in the accumulation than in the ablation part of the glaciers (see also section 4.2; Fig. 10). However, the general climate information is essentially the same for the evolution of both glaciers, since the two series are very similar when detrended (Fig. 8). Likewise, Reference Vincent, Kappenberger, Valla, Bauder, Funk and Le Meur.Vincent and others (2004) have shown from observations that four Alpine glaciers (including Glacier de Saint-Sorlin) have similar evolution in time when the long-term trends are adjusted.

Fig. 8. Cumulative centered mass balance for Glacier de Saint- Sorlin and Glacier d’Argentière after the 1981–2003 linear trend for each glacier has been subtracted.
One may discern four distinct periods in the glaciers’ evolution through 1981–2003 (Figs 4 and 8): a first, relatively regular and moderate, ablation period from 1981 to 1988 is interrupted by a sharp increase in melt for 3 years (second period) followed by a near-equilibrium plateau (third period). Finally (fourth period), after 1997 the glaciers lose mass again, at a more sustained rate than in the first period.
4. Climate Sensitivity of the Glaciers’ SMB
4.1. Modeling approach
The surface and internal physical processes of snow and ice energy and mass exchange and transformation are explicitly represented in our modeling approach. Also, the snow/ice model is explicitly and separately driven by the various meteorological terms that determine the SMB. The model is therefore particularly suited to evaluating climate-change impact on glaciers beyond periods for which the glaciers have been monitored, either in the past or in the future. Climate models provide climate-change scenarios which may be regionally meaningful, particularly if mesoscale regional models (Reference SchärSchär and others, 2004) or stretched-grid global models (Reference Deque, Marquet and JonesDeque and others, 1998) are used. At present, however, no such model can provide meteorological information at the fine spatial and temporal resolution necessary for physically based modeling of glacier SMB. Downscaling climate change from large-scale models to the glacier scale is a major issue when considering modeling glacier change in response to climate change.
We avoid this issue here by addressing glacier sensitivity rather than glacier change, which will be the topic of future papers. Sensitivity is evaluated with respect to variations in the various surface meteorology parameters that may occur due to climate change. In the real world, all parameters vary concurrently, so comparing past records for climate and glacier variability has provided estimates of combined sensitivity (Reference VincentVincent, 2002), but limited understanding of the relative contribution of the various meteorological parameters. Degree-day models can tentatively separate contributions of precipitation and of an integrated energy- balance term (Reference Braithwaite and ZhangBraithwaite and Zhang, 2000). In our approach, the relative influence of temperature, wind, moisture, precipitation or radiation can be evaluated separately by applying anomalies one by one on the original SAFRAN input parameters to Crocus.
To provide a synthetic picture of the sensitivity of glaciers at different altitudes and with various exposures, a demonstration glacier is defined on an idealized mountain slope. The mountain is a cone culminating at 3600ma.s.l. (maximum altitude of SAFRAN meteorological data), with a constant 20° slope in all directions. We present our results for glaciers located in the Mont Blanc area, Haute Savoie, France. We use the SAFRAN-disaggregated meteorological data for this area over the 1981–2003 period. The reference (unaltered SAFRAN meteorology) and sensitivity simulations all last 23 years to fully preserve interannual variability as sampled in the SAFRAN data. We have performed two simulations: one where no precipitation adjustment has been done on SAFRAN data, and the second where SAFRAN precipitation has been multiplied by 1.5, which is the mean multiplying factor on Glacier de Saint-Sorlin and Glacier d’Argentière with little dependence on altitude.
At the beginning of a simulation, the whole cone is covered with glacier ice of sufficient initial thickness to prevent full melting. The topography and surface elevation are unaffected by changes in the ice thickness during the simulations. As expected, the SMB increases with elevation everywhere on the demonstration glacier, and is higher on the north face and lower on the south face, at a given elevation. The altitudinal distribution of the SMB is shown for the north face in Figure 9. Two aspects of the simulated SMB sensitivity to climate change are presented and discussed below. The first is the mass balance of the north face because north is the most common exposure for Alpine glaciers. Then, the ELA averaged over all exposures provides a practical single number to synthesize overall changes of the glacier SMB in response to altering the input meteorology.

Fig. 9. Mass-balance profile for a synthetic glacier in Mont Blanc area. Orientation of the profile is north; slope is 20°. Solid line is for unaltered SAFRAN precipitation; dashed line is for precipitation multiplied by 1.5.
4.2. Surface mass-balance sensitivity
The simulated north surface mass-balance (NSMB) profile is shown in Figure 9 for unaltered meteorological data input into the model, except precipitation for which two cases are presented: unaltered, and multiplied by a 1.5 correction factor. In the latter case, the simulated NSMB curve is similar to the unaltered-precipitation case, but shifted 200m down in altitude. The mean mass-balance gradient is 9mmw.e. m–1 in the ablation area (2000–2920 m), 2.5mmw.e. m–1 in the accumulation area (2920–3600 m) and 5.8mmw.e. m–1 near the equilibrium line (2920 m), with a rapid change at the ELA. The NSMB sensitivity to the various meteorological parameters is shown in Figure 10 in the case where reference precipitation is uncorrected, and results for corrected (×1.5) precipitation are also discussed. The range through which sensitivity to each meteorological parameter is tested is typical of the amplitude of 21st-century climate change simulated by global climate models for the Alpine region with A2 scenarios from the Intergovernmental Panel on Climate Change. The cloudiness parameter in input to the Crocus model only affects the spectral characteristics of radiation, not the downward radiation intensity which is a separated meteorological input. Sensitivity to the cloudiness parameter is thus hard to interpret and not evaluated here.

Fig. 10. Mass-balance sensitivity to various meteorological parameters as function of altitude for surface temperature (a), wind (b), relative air moisture (c), precipitation (d), downward longwave radiation (e) and solar radiation (direct+diffuse) (f). Dashed line in (a) describes mass- balance variation due to temperature variation and corresponding longwave radiation variation. SAFRAN precipitation here is uncorrected.
Changing surface temperature alone is numerically acceptable but may be meteorologically inconsistent. For instance, precipitation may be prescribed as solid in the original SAFRAN meteorology, consistent with the original temperature but possibly inconsistent if temperatures are increased in a sensitivity experiment. To prevent such inconsistency, the precipitation phase is adjusted when the temperature is altered so that no solid precipitation occurs when the air surface temperature is above 1.5°C. One also expects the atmospheric longwave radiation to increase at warmer temperature. However, longwave radiation is not uniquely defined by surface air temperature. It also varies with atmospheric moisture or cloud cover. Thus, the sensitivity to altered temperature is separately evaluated with and without concurrent alteration of the downward longwave radiation (Fig. 10a). A Stefan–Boltzmann temperature dependence of the downward infrared radiation with surface temperature (Reference Greuell, Genthon, Bamber and PayneGreuell and Genthon, 2003) is used in the former case.
The sensitivity of the NSMB is larger in the ablation than in the accumulation area for all meteorological parameters except for precipitation at low elevations. This is due to the albedo feedback when the surface changes from high- albedo snow to low-albedo ice, a phenomenon that can only occur in the ablation area. In addition, all the sensitivity profiles with altitude are asymmetric with respect to the sign of the meteorological alteration, reflecting the fact that the equilibrium line, and thus the transition between a more sensitive ablation region and a less sensitive accumulation region, descends as the SMB increases. This asymmetry is particularly visible for temperature (Fig. 10a) since this is the meteorological variable for which the larger SMB changes are obtained.
Near the equilibrium line, the NSMB sensitivity to precipitation is also higher in the ablation than in the accumulation regions. However, further below, the sensitivity decreases with altitude (Fig. 10d) because it is assumed, in line with all meteorological parameters except temperature, that any change in precipitation is proportionally the same at all elevations. Because precipitation increases with altitude, so does the absolute change in precipitation for the same prescribed relative change. Air moisture, on the other hand, generally decreases with altitude, so the sensitivity with altitude of a proportional moisture change is amplified compared to other meteorological parameters (except wind), as indicated by the steep vertical slopes in Figure 10c. The fact that more moisture induces less SMB may appear surprising. However, when air moisture increases, the vertical gradient of moisture in the surface atmosphere is generally decreased, as is the turbulent latent- heat flux. As the surface cools and evaporates less through latent-heat transfer to the atmosphere, more heat is available at the surface to melt more snow or ice.
A wind increase decreases the mass balance by augmenting the sensible-heat flux, since this flux is positive from air to snow/ice and brings energy to the surface for most of the year. Because air temperature is closer to glacier surface temperature at higher elevation, the wind effect also decreases (by decreasing of the turbulent flux). Thus, here again, the vertical gradient of NSBM sensitivity is larger than for other meteorological variables (Fig. 10b). Note that wind is a parameter likely to affect a glacier-controlled surface air layer, so ignoring such layers (section 3.1) might bias the estimated sensitivity. As expected, any increase in long- and shortwave radiation decreases the mass balance (Fig. 10e and f). However, this process is much more efficient for the long waves since the surface albedo is much higher in the solar than the thermal wavelength.
The results listed above are essentially preserved if reference precipitation is corrected with a 1.5 multiplication factor. All the curves plotted in Figure 10 are shifted down in altitude (not shown) to reflect a larger mean SMB (Fig. 9) and thus a lower snowline. For temperature, however, a slightly larger sensitivity is found in the ablation region. This difference can be explained by a combination of the amount of snow accumulated during winter (depending on precipitation multiplying factor and temperature change for snow/rain transition) and the fact that turbulent fluxes are larger over ice than snow due to greater roughness length.
An important result of the present study, already suggested by Reference Oerlemans and HoogendoornOerlemans and Hoogendoorn (1989), is that because the SMB sensitivity to any meteorological alteration is altitude-dependent, the vertical gradient of mass balance is not conserved in a climate change. Thus, prescribing fixed vertical SMB gradients when studying the impact of climate change on glaciers can result in significant errors.
4.3. Equilibrium-line altitude sensitivity
The mean ELA is a pertinent and practical synthetic indicator of glacier response to climate change. In particular, a glacier can survive climate warming only if its ELA does not exceed the glacier upper boundary. On our synthetic glacier with unaltered meteorology, the ELA is at 2920 m on the northern face and 3080 m on the southern face. The ELA averaged over all exposures is at 2988 m. Sensitivity of the mean ELA to the various meteorological parameters is presented in Figure 11. Here, the range of variation for temperature is limited to [–3°C;3°C] because a temperature warming above 3°C places the ELA outside the glacier limits. ELA sensitivity to temperature, either alone or combined with downward radiation, is linear in this range (Fig. 11a). So are sensitivities to wind, moisture and radiation (Fig. 11b, c, e and f), while sensitivity to precipitation is almost linear (Fig. 11d).

Fig. 11. Model sensitivity of ELA to surface meteorology. The printed mean sensitivity is the equation of linear fit. (a) Sensitivity to temperature variation. (b–f) Sensitivities to wind (b), air moisture (c), precipitation (d), downward longwave radiation (e) and solar radiation (f), with variations expressed as fractions. Dashed line in (a) describes mass-balance variation due to temperature variation and corresponding longwave radiation variation. SAFRAN precipitation here is uncorrected.
According to the model, the ELA sensitivity to temperature is 125 m °C–1. Here, sensitivity to temperature, and other sensitivities henceforth, are evaluated with respect to the annual mean SMB, not just the summer ablation as is often done in other studies (Reference VincentVincent, 2002). As a result, the sensitivity accounts for the impact of temperature on, not only the summer ablation, but also the length of the ablation season which increases in a warmer climate. When taking into account an increase in longwave incoming radiation as temperature increases, the sensitivity of the ELA to temperature is substantially increased and reaches 160 m °C–1. These values are much larger that those recently reported by Reference VincentVincent (2002), in the range 60–70m °C–1. Other authors (Reference Oerlemans and HoogendoornOerlemans and Hoogendoorn, 1989; Reference Wallinga and van de WalWallinga and Van de Wal, 1998; Reference Greene, Broecker and RindGreene and others, 1999) suggest ELA sensitivity (~Ί20–140 m °C–1) in closer agreement with ours, but Reference VincentVincent (2002) raises questions about the methods used. There are also differences between our approach and Reference VincentVincent’s (2002), which can explain different sensitivities. Reference VincentVincent (2002) relates the cumulated summer positive degree-days estimated from valley meteorology to the measured summer SMB at various altitudes on various glaciers in the French Alps. However, the variations in duration of the summer season are not taken into account. This underestimates the sensitivity since a warmer climate is likely to expand the ablation season. In addition, regressing degree-days to ablation integrates the effect on ablation of not only the actual temperature above the glacier, but also all other meteorological variables that affect ablation and may change along with temperature. For instance, if summer precipitation increases with temperature, it is likely to be liquid, and then to run off on ice on the bottom part of the glacier (very little influence on ablation), but on the snow-covered parts of the glacier this precipitation could be stored in the snowpack and contribute to accumulation. This induces lower sensitivities than when temperature alone, or along with induced longwave radiation, is considered. Also, winter precipitation, if increasing with warmer temperature, can delay melting away in summer and, through albedo feedback, significantly reduce summer ablation. Sensitivity is again decreased. Cloud cover is also likely to change with temperature. Furthermore, Reference VincentVincent (2002), in his calculation of ELA change with climate, assumed a vertical gradient of SMB of 7–8 mm w.e. m–1. This is estimated from Reference Haeberli and HoelzleHaeberli and Hoezle (1995), who used a fixed altitudinal SMB gradient. This is questionable, as mentioned in section 4.2 (Fig. 9). In the present study, the present-day vertical gradient at the ELA is only 5.8 mm w.e. m–1. Because of this difference, the same SMB change results in a larger ELA change here than in Reference VincentVincent (2002). However, because the sensitivity to climate change varies with altitude (Fig. 10), the vertical gradient of SMB is expected to change in a changing climate. Finally, various estimates of glacier sensitivity to climate found in the literature (Reference Oerlemans and FortuinOerlemans and Fortuin, 1992; Reference Wallinga and van de WalWallinga and Van de Wal, 1998; Reference Greene, Broecker and RindGreene and others, 1999; Reference VincentVincent, 2002) are generally not directly comparable because temperature, precipitation and other climate variables are not always similarly separated.
Our modeling approach makes this separation possible (Figs 10 and 11) and the comparative influence of each meteorological variable on ELA is summarized in Table 3. This table lists, for each variable, the amplitude of change necessary for a 160 m rise in ELA, i.e. the equivalent of a 1 °C warming taking into account the associated downward longwave radiation increase. For surface relative air moisture and wind, a large (44% and 81% respectively) increase is required. It takes a 28% decrease in precipitation to have the same impact as a 1 °C increase in surface temperature. This is halfway between Reference OerlemansOerlemans' (1981) and Reference Raper, Brown and BraithwaiteRaper and others' (2000) estimates (20% and 35% respectively). The global-average annual mean precipitation is expected to increase by only a few per cent for each degree of warming (Reference ChurchChurch and others, 2001). Although regional effects may be important, the future evolution of Alpine glaciers is unlikely to be dominated by precipitation changes. Radiation, which may in particular be affected by cloudiness in a changing climate, also has significant impact on the SMB.
Table 3. Influence of each meteorological variable on the mean SMB on the demonstration glacier, equivalent to a 160 m rise in ELA

5. Conclusions
Because the SMB of glaciers is determined not only by temperature and precipitation but also by wind, moisture and radiation which affect the surface energy budget, glacier response to climate change may be more complex than overly simplified models can account for. Here, a SMB model that explicitly resolves the various meteorological parameters of importance, the associated processes of mass and energy exchange and disposal, the geometrical aspects (altitude, surface exposure) of the glaciers, and the evolution in time of meteorology and climate at sub-diurnal scales, is described and validated, then applied to evaluate the sensitivity of glacier SMB to changes in climate. The glacier SMB model is based on the Crocus snow model that was previously developed for seasonal snow analyses and avalanche forecasting. Meteorological input to the model is provided by SAFRAN, an analysis and disaggregating tool also developed in the framework of avalanche forecasting. The model is found to perform well on two glaciers in the French Alps, and in particular to reproduce the observed interannual variability of the integrated and local SMB and of the ELA. This is obtained without explicit tuning of the model itself, although the spatial distribution of precipitation from SAFRAN at the sub-glacier scales had to be adjusted, and the albedo of ice surfaces had to be prescribed from observations in the field. Alpine glaciers have been retreating in the last century. The test period here, 1981–2004, is found to be a period of accelerated melt, in spite of a temporary recess in the early 1990s.
Because all components of the mass and energy budget are separated, the SAFRAN/Crocus modeling tool offers a unique means of evaluating the separate influence of various meteorological parameters on glacier SMB changes. In the range of variation suggested by global models of 21st- century climate, temperature is confirmed as a main actor. The ELA sensitivity is estimated at 125 m °C–1, or even 160 m °C–1 if a concurrent change in the downward longwave radiation is taken into account. Everything else on hold, a 5°C warming is thus expected to raise the ELA by 800 m, which would be enough to doom many glaciers to extinction. Although precipitation may increase with climate warming, it is unlikely to fully compensate for the temperature effect. As the quality of climate-model predictions on regional scales is unverified, the actual contributions of wind, atmospheric moisture and radiation to the evolution of glacier SMB in the future will be hard to establish, but our results are a quantitative demonstration that they should not be neglected.
The results presented here (Figs 10 and 11; Table 3) may be used as a toolbox for a preliminary estimation of the impact on glacier SMB of any combined change of meteorological parameters associated with climate change. However, this necessarily remains a crude estimation, as combined effects between responses to the various meteorological parameters are not taken into account. Running the full model for a range of scenarios detailing the evolution of the various pertinent meteorological parameters will be the only way to fully predict the response of glaciers to climate change. Downscaling from global or even regional models to glacier scales will then be a crucial issue.
Acknowledgements
This research is part of the Climate Change and Cryosphere project funded by the French Ministry of Research/National Institute for Cosmic Sciences (INSU) (Action Concertée Incitative Changement Climatique). Satellite images were provided by Centre National d’Etudes Spatiales, France, and Spot-Image (ISIS0412-725). We thank Y. Durand for help with SAFRAN data. We thank the many people who contributed field measurements on Glacier de Saint-Sorlin and Glacier d’Argentière, and those who created and developed free softwares (GNU General Public License) used in our research, in particular the Generic Mapping Tools (GMT) and xmgrace. We thank the scientific editor H. Rott and the reviewers R. Hock and B. Brock, who significantly helped us to improve the quality of the paper.
















