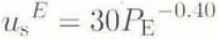Introduction
The first worker to show scientifically that velocity variations on glaciers were correlated with variations in temperature and rainfall was Reference Forbes,Forbes (1842). His study on Mer de Glace indicated that accelerated motion occurred when temperatures were high and when precipitation occurred. The reason for this correlation, variations in basal water pressures induced by variations in water input to the glacier, remained unclear until studies by Reference Meier,Meier (1960) and Reference Müller, and Iken,Müller and Iken (1973). Since then many similar studies have been undertaken (e.g. Reference Hodge,Hodge, 1974; Reference Iken,Iken, 1978; Reference Iken,Iken and others, 1978; Reference Iken, and Bindschadler,Iken and Bindschadler, 1986; Reference Kamb, and Engelhart,Kamb and Engelhart 1987; Reference Fahnestock,Fahnestock 1991).
Water pressure appears to influence sliding in three ways: (1) sustained high pressures increase separation of ice from the bed, thereby increasing the shear stress on parts of the bed still in contact with the ice, (2) both transient and sustained high pressures exert a force in the down-glacier direction in cavities formed in the lee of irregularities on the bed (hydraulic jacking), and (3) by weakening subglacial sediments. The second idea was proposed by Reference Iken,Iken and others (1978) and has been modelled by Reference Iken,Iken (1981). Reference Iken, and Bindschadler,Iken and Bindschadler (1986) concluded that variations in surface velocity observed on Findelengletscher were a result of hydraulic-jacking effects at the bed.
This study focuses on velocity records similar to those used by Iken and Bindschadler in order to investigate variations in velocity observed on Storglaciären, Sweden.
Previous Work on Storglaciaren
Storglaciären (67°55’N, 18°35’E) is a small, temperate glacier located on the eastern side of the Kebnekaise massif in Lappland, northern Sweden. The top 30–40m of the ice in the ablation area is below freezing temperature throughout the season (Reference Hooke,, Gould, and Brzozowski,Hooke and others, 1983a; Reference Holmlund, and Eriksson,Holmlund and Eriksson, 1989), whereas the rest of the glacier, including the ice below the layer in which temperatures fluctuate annually in the accumulation area, remains at the melting point. Reference Brzozowski, and Hooke,Brzozowski and Hooke (1981) and Reference Hooke,, Brzozowski, and Bronge,(Hooke and others 1983b, Reference Hooke,, P,, Holmlund,, Nilsson, and Stroeven,1989) studied the variations in surface velocity during the period 1979–85. Their studies revealed a seasonal pattern with high velocity peaks occurring in early summer and, in some years, gradually decreasing velocities as the melt season progresses. The glacier also reacts to sudden inputs of water from rainstorms. The internal drainage system of the glacier has been studied extensively (Reference Stenborg,Stenborg, 1965, Reference Stenborg,1969; Reference Nilsson, and Sundblad,Nilsson and Sundblad, 1975; Reference Holmlund, and Hooke,Holmlund and Hooke, 1983; Reference Holmlund,Holmlund, 1988a, Reference Holmlund,b; Reference Hooke,, Miller, and Kohler,Hooke and others, 1988; Reference Seaberg,, Seaberg,, J,, Hooke, and Wiberg,Seaberg and others, 1988; Reference Hooke,Hooke, 1991; Reference Kohler,Kohler, 1992; Reference Hock, and Hooke,Hock and Hooke, 1993; Reference Hooke, and Pohjola,Hooke and Pohjola, 1994). From these studies it is clear that there is a difference in the drainage systems of the lower and upper parts of the ablation area. The overdeepened upper part seems to drain largely The lower part drains faster and largely subglacially, and the characteristics of its subglacial drainage change during the melt season. In the early summer it probably consists of many smaller conduits; as the season progresses, this system develops into one consisting of fewer, larger conduits which transport the water more efficiently.
Experimental Procedure
In March 1985 two stake nets, net 45 and net 23, each consisting of five stakes, were established on the glacier. This configuration of stakes was used during the 1985–87 field seasons. Only the 1987 data are discussed here, as that is the only time period for which there is a corresponding water-pressure record.
The stakes were made of 6 m long, 50 mm diameter, steel pipes. The diagonals of the nets were scaled to reflect the average local thickness of the glacier. The nets were located slightly down-glacier (45) and up-glacier (23) from a transverse bedrock ridge, or riegel, in the bed (Fig 1). These locations were chosen to provide information on changes in flow as the glacier crossed the riegel. The stakes were originally set so that the top projected ~0.5m above the snow surface. As melting progressed the stakes were cut in increments of 1 000 ± 0.002 m, thus maintaining a minimum height of ~0.5 m above the ice surface. The length of each stake remaining in the ice was monitored carefully throughout the season and stakes were replaced well before they melted out. On days when stakes were cut or replaced, they were normally surveyed both before and after cutting, usually with only 1–2 h between the surveys.
Horizontal and vertical angles and horizontal distances to the individual stakes were measured from a fixed point on the northern side of the glacier (A72 in Figure 1) by means of a Geodimeter 140 total station. The internal distances in the strain nets were measured with a Geodimeter 12A distance meter in order to permit a least-squares estimate of the location of the stakes in the local coordinate system.
Surveys were usually made between 1000 and 1300 h daily, weather permitting. The distances measured by the Geodimeter 140 were adjusted for temperature and barometric-pressure effects.
The standard error in the distances measured by the Geodimeter 140 is, according to the manufacturer, ± (5mm + 3ppm.). Based on the reproducibility of measurements, the standard error in the horizontal angles is estimated to be ±3’. The average errors in the measured distances, based on average distances to stake nets 45 and 23, are ±6.2 and ±6.8 mm, respectively, and the errors in the directions perpendicular to the vector from the instrument to the net are ±6.0 and ±8.7 nun. respectively.

Fig. 1. Map of the ablation area of Storglaciären showing generalized surface and bed topography, fixed points, and locations of velocity stakes. Insert shows details of the strain stake nets.
The standard error in the distances measured by the Geodimeter 12A is ±(5 mm + 10 ppm.), which implies that the maximum error in these distances is ±6 mm.
The uncertainty in the vertical angle measurements made with the Geodimeter 140, as estimated from reproducibility of repeated measurements, is ±2’, producing vertical uncertainties of 4.0 and 5.8mm to net 45 and net 23, respectively. The uncertainty in the vertical position of a given point is a combination of this uncertainty and that due to changes in atmospheric refraction or incorrect adjustment for refraction. The resulting uncertainty of the vertical positions is estimated to be 5–6 mm.
The least-squares adjustment that was made in order to establish the locations of the stakes in the horizontal plane provided an additional estimate of the standard error of these coordinates. In general the error is ±(6–8 mm). Some surveys yielded larger errors; these were either discarded or incorporated with the knowledge of their limitations, depending on the severity of the errors. Based on the uncertainties in the stake positions given above, typical errors in the horizontal velocities are generally < ± 10 mm d−1 for surveys 1 d apart. The error decreases for longer surveying periods.
A large number of boreholes was drilled on Storglaciären during this study for a variety of reasons, including water-pressure measurements, borehole-deformation studies and tracer experiments. The drilling was done with a hot-water drill The boreholes in the lower part of the ablation area were inferred to he connected to the main sub- or englacial drainage network if the water level in a borehole suddenly dropped and then remained low during the rest of the drilling and, more importantly, if the level fluctuated after drilling was complete. Sensors, originally designed for measuring oil pressure in automobile engines, were placed in the holes and connected either to a chart recorder or to data loggers. The changes in resistance of the sensors were converted to a measurable signal through a standard Wheatstone bridge. The sensors were calibrated at the time of installation by lowering and raising the sensor in the borehole while recording its depth below the ice surface, the depth to the water surface from the ice surface, and the resistance of the sensor. The accuracy of the water-pressure measurements is ±3–4 kPa, corresponding to a change in water level of ˜3–4m. The largest uncertainty is due to hysteresis of the sensor and different electronic factors, such as unknown cable resistance, temperature dependence of the bridge, and so forth.
Most of the climatic data used in this paper were gathered with standard meteorological equipment at the Tarfala Research Station. The database consists of hourly and daily averages of air temperature and hourly and daily totals of precipitation. Records of hourly totals of precipitation were also gathered on the glacier.
Overview of Glacier Hydrology
As noted earlier, there is a perennial layer of cold ice at the glacier surface which forms an impermeable barrier through which the meltwater cannot percolate. Thus, the principal places where meltwater enters the glacier, outside the accumulation area, are crevassed areas at the equilibrium line and in the region around the riegel. Because the snow cover is much thinner, on average, in the ablation area than in the accumulation area (Reference Schytt,, Jonsson, and Cederstrand,Schytt and others, 1963; Reference Schytt,Schytt, 1965, Reference Schytt,1966, Reference Schytt,1968; unpublished information from Tarfala Research Station, 1985–87), and because of higher temperatures at lower elevations, the snowpack on the lower part of the ablation area becomes saturated earlier than that higher on the glacier. This means that water can enter the glacier earlier at the lower water-input area than at the upper one.
Basal water pressures in the large, overdeepened upper part of the ablation area are generally close to, or sometimes, briefly and locally, slightly in excess of the overburden pressure (Reference Hooke,Hooke, 1991; Reference Hooke, and Pohjola,Hooke and Pohjola, 1994). The amplitude of the variations during most of the season is only ~10% of the overburden pressure. The lower part of the ablation area is better drained and exhibits a much lower average water pressure. The amplitude of variations in this part of the glacier frequently exceeds 75% of the overburden pressure (Reference Hooke,, P,, Holmlund,, Nilsson, and Stroeven,Hooke and others 1989; Reference Hooke,Hooke, 1991).
Velocity Data
During the summer there is a rather rapid acceleration of the glacier in early to mid-June (Fig. 2). The timing of this event depends on when the air temperature rises above 0°6 for a prolonged period. Because the winter discharge is small (Reference Stenborg,Stenborg, 1965) the drainage network is not dimensioned for the sudden increase in water flux.

Fig. 2. Horizontal and vertical surface velocity and azimuth of the horizontal velocity component. Vertical bars show the estimated error in the velocity for a 1 d survey interval. Precipitation and temperature from Tarfala Research Station.
In 1987, the acceleration event in stake net 45, is a well-defined, broad peak correlated with the seasonal increase in temperature in June (Fig. 2). Maximum velocities during this event are up to ~60 mm d−1. The pattern of velocities in net 23 during the same period differs in that the peak is less well-pronounced. The onset of accelerated motion occurs simultaneously with that in net 45; however, net 23 exhibits multiple peaks during the acceleration event in contrast to the broad single peak in net 45.
The acceleration is probably initiated at the riegel when the snowpack in the crevassed region is at the melting point throughout. It is unlikely that water mput at the equilibrium line contributes much, because the snowpack there is generally thicker than at the riegel and thus requires more time to reach the melting point. Hence, significant water input at the equilibrium line starts later than in the riegel area
When daily water inputs are comparatively constant, the surface velocity, uS , decreases as the melt season progresses, reaching relatively stable values by the end of August. Such was the case in 1982 and 1983 (Reference Hooke,, Brzozowski, and Bronge,Hooke and others, 1983b), but the trend is less obvious in the present data because of large peaks late in the season associated with major precipitation events or periods of unusually high temperature. Such peaks are discussed in more detail below.
Unlike in previous years (Reference Hooke,, Brzozowski, and Bronge,Hooke and others, 1983b, Reference Hooke,, P,, Holmlund,, Nilsson, and Stroeven,1989) the vertical velocity does not undergo any seasonal change in 1987. However, there is a response to the June acceleration event in net 45 (Fig. 2). At the time of the onset of the event the vertical-velocity peaks attain a positive value close to the maximum for the season. As the horizontal velocity increases, the vertical velocity drops to a low.
The azimuth, ω, of υ s, does not undergo any seasonal change.
On shorter time-scales, variations in u s can be correlated with variations in both air temperature and precipitation. The importance of temperature peaks in producing velocity highs decreases during a season. The relative importance of precipitation thus increases. This results from the development of a more efficient drainage system as the season progresses. The drainage system adapts to an effective input rate, determined by average meteorological conditions. Thus, peaks in melt provide only a modest increase in input rate over the mean daily rate, whereas precipitation may produce a much larger increase, depending on the rainfall intensity. When precipitation occurs over longer periods, the average input rate will he higher, consequently enlarging the conduit system. Larger excursions from the mean input rates arc thus needed late in the season to produce a velocity peak of a given magnitude. An example of a temperature-influenced, and thereby melt-rate-influenced, peak can be found on Julian day 201 (marked by Tl in Figure 2). Good examples of precipitation-induced velocity peaks (marked by P1 and P2 in Figure 2) are found on Julian days 188 and 214.
The major differences between stake nets 45 and 23 are in the magnitudes of the major velocity peaks and in the amplitudes of the variations in the two nets. Net 45 shows several peaks reaching and even exceeding 60 mm d−1, ~200% of the average winter velocity, with an amplitude of ~40 mm d −1. The velocities in net 23 are almost never this high; the maximum in 1987 was 54 mm d, ~170% of the average winter velocity, with an amplitude of ~24 mm d−1.
Variations in the direction of the surface-velocity vector in net 45, w, seem to he weakly correlated with changes in velocity. However, the uncertainty in w is much larger (~7°) than the variations. Hence, such a correlation is speculative at best.
Results from a force-balance calculation by Reference Hooke,, P,, Holmlund,, Nilsson, and Stroeven,Hooke and others (1989) indicate that the basal shear stress changes significantly in the lower part of the ablation area, with increases reaching 84% relative to winter values. The upper part of the ablation area shows a negative change relative to winter values of ~20–40%. Since water pressures remain high in the upper part of the ablation area throughout the summer season, the basal drag probably remains low. The lower part of the ablation area, on the other hand, experiencing water-pressure variations of high amplitude, is expected to accelerate and decelerate in response to these variations. The variations in basal drag indicated by Reference Hooke,, P,, Holmlund,, Nilsson, and Stroeven,Hooke and others (1989) calculations support this notion. The velocity record of net 23 shows smaller variations than that of net 45 The former may thus he partly caused by longitudinal coupling to the lower part of the ablation area.
The Water-Pressure Record
Figure 3 shows part of the 1987 velocity record together detailed water-pressure measurements from two boreholes, B875 and B876 (Fig. 1), hourly average discharges from the two proglacial streams, Nordjokk and Sydjokk (Fig. 1), hourly average temperature and hourly precipitation. The two records of water pressure are similar except for two periods. During the first period, days 200–203, the water pressure in B876 rises close to the expected overburden pressure and fluctuates slightly while that in borehole B875 exhibits a diurnal signal. The most likely explanation for this discrepancy is that B876 lost its connection to the subglacial drainage system during this period. The hole seems to regain its connection to the main drainage system again as water pressures in B875 rise during day 203. The second period of ambiguity starts on day 209 and continues through the rest of the record. This time, Β876 seems to lose all connection with the main drainage system. On day 215, water levels in this hole drop dramatically. The significance of this drop and the subsequent slow increase, also seen in the last part of the B875, record, is not understood. Large temperature fluctuations during days 221–224 seem not to affect either water-pressure record. These fluctuations may be compared with the temperature and water-pressure peaks of days 207 and 209, which show a good correlation. One hypothesis might be that the water input during the period of rain, days 212–219, was able to so enlarge the subglacial drainage network that increases in meltwater flux due to temperature fluctuations were too small to affect the pressure in the system. It is possible too that B875 lost connection with the main drainage system. It is also possible that the slow rise in water pressure reflects the closure of conduits. However, it is not clear why there are no diurnal variations in this signal in response to temperature variations and hence melt-rate variations.

Fig. 3. Horizontal and vertical velocities in slake nets 45 and 23, discharge from Nordjokk and Sydjokk proglacial streams, the ratio of Nordjokk over Sydjokk discharge, and water-pressure measurements in boreholes 875 and 876. Hourly average temperature was recorded at Tarfala Research Station and hourly precipitation totals were recorded on the glacier.
The water-pressure peaks occurring on days 207 and 209 seem to be correlated with pronounced temperature peaks on the same days. The lag between the temperature and water-pressure peaks on these two occasions, 4–5 h, is consistent with the lags between similar peaks elsewhere in the record (as on days 199–201). However, more pronounced temperature peaks earlier in the record did not yield responses of similar magnitude. This may be due to the higher average water-pressure conditions during the early part of the record. The water-pressure peak on day 207 occurs after a period of low temperatures and thus low water input to the glacier. Hence, significant closure of the conduits may have occurred during the period leading up to day 207. It is also possible that the peak resulted from some local event related to the subglacial drainage network, but the consistent time lag between the different temperature peaks and associated water-pressure peaks suggests that the peaks are a direct response to meltwater input changes.
The discharge curves in Figure 3 provide further on the importance of the water-pressure curves. The two streams, Nordjokk and Sydjokk (Fig. 1), drain different parts of the glacier (see, fur example, Reference Stenborg,Stenborg, 1969; Reference Kohler,Kohler, 1992). Sydjokk water originates mainly in the moulin area above the riegel. High sediment concentrations in the water suggest that the drainage is mainly subglacial. Nordjokk water originates in the accumulation area and passes through the overdeepened area upglacier from the riegel. The transit time for the Sydjokk water, measured from the input point at the moulins to the Sydjokk weir located 200 m downstream from the glacier terminus, is between 45 min and 2 h (Reference Kohler,Kohler, 1992). The transit time is a function of discharge (Seaberg and others, 1988) but also decreases as the drainage network develops through the season.
The water pressure recorded in boreholes B875 and B876 should be compared with the Sydjokk discharge. A major peak in discharge on days 216–217 coincides with a large drop in water pressure from high values. This implies that water pressures rise because of an increase in water input. The increased water pressure is needed to drive the water through an under-dimensioned drainage system.
The Effect of Water-Pressure Variations on Surface Velocity
The water-pressure record (Fig. 3) indicates that the basal water pressure must be more than ±0.5 M Pa, corresponding to approximately half the overburden pressure, to cause a major acceleration. The first period of such water pressures, days 199–204, corresponds with a velocity peak in net 45. The velocity low in the middle of this broad peak corresponds to the period of lower water pressures. Velocities were again high during another period in which water pressures exceeded 0.5 M Pa, days 211–218. It is also interesting that the velocity low during days 205–206 corresponds to low water pressures during the same period. The effects of water pressure on the dynamics of the glacier are described in more detail below.
The two short-term pressure peaks during days 207 and 209 are also of interest since they do not correlate directly with any significant change in velocity. The small peak in velocity between days 208 and 209 docs not overlap with the second of these water-pressure peaks. As borehole B875 froze shut only 3 d after the pressure transducer was installed, water inputs from the surface directly to the hole did not cause the peaks. This discrepancy may be explained in one of three ways:
-
1. The velocity peak is induced elsewhere, by either a push from up-glacier or a pull from down-glacier.
-
2. The velocity peak may be caused by measurement error. Although there is no reason to believe that this is the case, it cannot be ruled out as a possible explanation.
-
3. The narrow water-pressure peaks are local and do not affect a large enough area of the bed to produce an increase in velocity. This does not provide an explanation for the velocity peak
The water-pressure record seems to indicate that the drainage system was well connected to the hole during the period in question. It is therefore difficult to explain the velocity peak in terms of water-pressure variations unless these were very local and not affecting the site where water pressures were being recorded. Longitudinal-coupling effects by means of a pull from down-glacier are therefore unlikely. This also applies to a possible push from up-glacier, since there is no reason to believe that this part of the glacier should accelerate without any observable cause. Furthermore, discharge measurements do not show any peaks during this period. This shows that no major water fluxes went through the drainage system that could have raised water pressures. It is thus concluded that the velocity peak may be the result of measurement errors and that the water-pressure peaks were not sufficiently large in duration or magnitude or both to produce an increase in velocity.
With the possible exception of the peaks on days 207 and 209, the water pressure recorded in borehole B875 is assumed to provide an accurate picture of global pressure variations under the lower part of the ablation area, or at least to reflect the conditions over a region incorporating stake net 45. This is supported by the similarity between the B875 record and earlier recordings of water pressure made in the lower part of the ablation area of Storglaciäaren (unpublished information from R. Hooke, 1985–94; Reference Hooke,Hooke, 1991).
Because the velocity record has a temporal resolution of 1–2d, and hence comprises averages over these periods. compared to 10 min for the water-pressure record, the latter was averaged over periods corresponding to the intervals of the velocity measurements. Velocity measurements during days 198–199 and 220–227 were omitted from the analysis. The first interval has an incomplete pressure record and the second was initially considered to reflect a problem with the pressure transducer. The data from these intervals will he discussed below in light of the analysis of the remaining data.
The water-pressure record can be converted to effective pressure, P E, by subtracting the water pressure, P w, from the ice overburden pressure, P 1.P E is of more interest since it figures directly in several proposed sliding laws. The overburden pressure was calculated from the depth of the borehole as given by the drilling logs. The daily average velocity was then plotted as a function of the average effective water pressure (Fig. 4). This approach is similar to one used by Reference Iken, and Bindschadler,Iken and Bindschadler (1986) except that they did not convert their water-pressure measurements to P E. As can be seen in the plot, considerable scatter is present. Neglecting the high velocity “outliers” (marked by circles in the figure), velocities seem to he more variable at higher values of P E (lower P W). This can also be observed in the Findelen-gletcher data (Reference Iken, and Bindschadler,Iken and Bindschadler, 1986, Fig. 6, p.105). One reason for this may be that the velocity fluctuations are more strongly influenced by longitudinal stress gradients at high P E, whereas lower P E tends to mask these gradients as the glacier responds more directly to high-water-pressure events. Alternatively, the water-pressure record may be more representative of global conditions when pressures are high and high pressures have persisted for several days. A power-law least-squares curve was fit to the data (dashed line in Figure 4). The choice of equation facilitates comparison between the data and several proposed sliding laws.

Fig. 4. Average surface velocity as a function of average effective pressure.
The anomalously high velocities (circles in Figure 4) can he an effect of the large fluctuations in water pressure during the periods in question. These data were removed and a second curve (solid line in Figure 4) was fit using the remaining points. The data removed will be discussed below. The curve is given by
where us E is the surface velocity (us E is used rather than to distinguish between surface velocity calculated from P E and measured surface velocity). The regression has an r2 of 0.90. If all data points are included, the value for r2 = 0.61 and the coefficient and exponent in Equataion (1) are 35 and −0.32, respectively. Assuming a constant driving stress and using Reference Nye,Nye’s (1965) flow theory, the internal-deformation component of the surface-flow vector is estimated to be ~4–5 mm d−1. This means that the sliding component would be ~80–90% of the surface velocity, consistent with studies of borehole deformation on Storglaciären (Reference Hooke,, Pohjola,, Jansson, and Kohler,Hooke and others, 1992). Subtracting the internal-deformation component from the velocity-data points in Figure 4, and fitting a similar equation, now describing the basal velocity, ub E, yield a coefficient of 24 and an exponent of −0.49 (r2 = 0.88)

Fig. 5. Velocity and effective-pressure data from Findelengletscher (Reference Iken, and Bindschadler,Iken and Bindschadler, 1986, table III, p.117) and Storglaciären. Solid line indicates power-law best fit of Storglaciären data described by Equation (1). Long-dashed line indicates power-law best fit of Findelengletscher data described by Equation (2).
Equation (1) can be used to calculate expected velocities from the original effective-pressure data. This provides a further test of the reliability of the regression.
Figure 6 shows the original velocity data (solid line) and the velocity calculated from Equation (1) (long-dashed line). Equation (1) models the observed velocity record well. However, it is to be noted that water pressures were linearly averaged even though the water pressure was inferred to be non-linearly coupled to the surface velocity. In order to estimate the magnitude of the errors thus introduced, a similar analysis was made on weighted averages. Since Equation (1) is a power law, average effective pressures were calculated using logarithmic values of the effective-pressure signal. The averages were then converted back to effective pressures and a regression made on these values. The results are a coefficient of 31 and an exponent of 0.42, r2 = 0.89. This indicates that the error introduced by the linear averaging was not significant for this data set. Comparisons between this data set and other studies are therefore justified, independent of the averaging scheme used in the individual study. Such a comparison is made below.

Fig. 6. Measured velocity from stake net 45 and velocity record calculated from power-law relationship between surface velocity and effective pressure.
Equation (1) can also be used to calculate a continuous velocity record from the water pressures (Figure 6, short-dashed line). However, because of the negative exponent in the power law, us E→∞ as P E→0. In reality the velocity is limited by drag on the sides of the glacier and, perhaps more importantly, by increased stress concentrations on local topographic highs on the glacier bed, as pointed out by Reference Lliboutry,Lliboutry (1987). The absolute magnitude of the largest peaks in the continuous calculated velocity curve (short-dashed line) must be viewed with this in mind.
Reference Pohjola,Pohjola (1993) and Iverson (personal communication, 1991) have measured sliding speeds on Storglaciären of > 100 mm d−1 with the use of borehole video cameras. The measurements indicate velocity fluctuations much larger than those recorded by daily averages, so the calculated velocity curve in Figure 6 is not unreasonable. It must also be remembered that the shorter-term variations seen in the calculated continuous curve would probably not be visible, at least not with the same amplitude, at the surface of the glacier. This is because basal velocity variations are likely to be attenuated by the ice as they are transmitted to the surface (Reference Balise, and Raymond,Balise and Raymond, 1985).
Pressure data from days 198–199 are incomplete and were not used in the power-law fits described above. However, assuming that the period missing from the water-pressure record during this interval does not significantly alter the average, the existing record can be used to cross-validate the reliability of Equation (1). The resulting velocity (shown as a square in Figure 4) agrees remarkably well with that measured (Fig. 6).
Days 220–226 were not included in the regression analysis because the water-pressure record for this period was initially interpreted as indicating a failure either of the recording sensor or of the connection of the borehole to the main drainage network. In view of the curve calculated from Equation (1) in Figure 6, however, it seems that the water pressure recorded may actually have reflected global pressures in the lower part of the ablation area, at least to the extent that it appears to determine the velocity in stake net 45. The smaller increase in measured velocity during days 222–223 is well within the standard error of the measurements. The three additional data points obtained for this period are shown as triangles in Figure 4.
If the four data points discussed above are included in the regression analysis, an exponent of −0.37 and a coefficient of 32 (r2 = 0.88) are obtained, not significantly different from the initial analysis yielding Equation (1).
If the velocity on days 208–209 is assumed to be a result of measurement errors, at least in part, there remain three aberrant periods: days 204–205,212–213, and 215–217, all of which correspond to large variations in water pressure. Interestingly, Equation (1) underestimates the velocity in all three periods. The reason for this is not clear, but it could be due to longitudinal-coupling effects or the effect of rising water pressure on velocity discussed by Reference Iken,Iken (1981) and Reference Iken, and Bindschadler,Iken and Bindschadler (1986). Reference Iken,Iken (1981) concluded, based on a finite-element model, that the highest velocities should occur during periods of rising pressure and not during peak pressure. Cavity growth is promoted by increased water pressures. The water-pressure changes associated with the peaks in Figure 6 are very large, corresponding to ~0.5P 1. Growth and decline of cavities in response to water-pressure fluctuations is not a linear process. If, for example, water pressures suddenly drop, cavities will decrease in size by plastic flow to a new equilibrium with the lower pressure. This means that velocities may remain high, and slowly declining, for several days after large pressure peaks. Initially, however, the velocity will decrease in response to the reduction in hydraulic jacking. This may help to explain anomalous velocities such as those of days 204–205 and 215–217. However, the natural glacier system is dynamic and probably never reaches a steady state. The intervals listed above all represent periods when the system is probably very far from a steady state and extreme velocities can be expected, especially at the rising limb of the water-pressure peaks. This indicates that the system is more strongly non-linear than Equation (1) would suggest. It is also evident that a sliding law should depend not only on P E but also on dP E/dt, especially when the changes in P E are large.
Comparisons Between Storglaciären and Findelengletscher
Reference Iken, and Bindschadler,Iken and Bindschadler (1986) published a record of water pressure and surface velocity from Findelengletscher similar to that discussed above for Storglaciären. Analyzing their data yields a relation
r2 = 0.77. This regression was done using all data considered reliable by Iken and Bindschadler. The exponents from the two regression Equations (1), and Equations (2), are nearly identical, suggesting a fundamental relationship (Fig. 6). Subtracting the inferred component of internal deformation, estimated by a similar calculation to that made for Storglaciären above, from the surface velocity and refitting the data yield a constant of 263 and an exponent of −0.61 (shown by the lower dashed line in Figure 6).
There are two high-velocity data points in Figure 5 of Reference Iken, and Bindschadler,Iken and Bindschadler (1986, p.105) that are not included in their table III. The values of P E (P E 1≈0.157 MPa and P E 2≈0.059 MPa) and us for these were read from their figure instead. They were not included in the regression, though, because their extreme character would influence the regression strongly while their values were not known as precisely as those of the rest of the data set. Inserting the approximate values of P E 1 and P E 2 into Equation (2) provides a test of the reliability of this relation:
Conclusions
Velocities in the ablation area of Storglaciären vary spatially and temporally. The bedrock ridge in the subglacial topography induces some of these variations because of its effect on the subglacial hydrology.
The lower part of the ablation area, down-glacier from the riegel, is influenced by daily variations in subglacial water pressure induced by precipitation and variations in melt rate. There is a good correlation between low effective pressure under this part of the glacier and surface velocity peaks. This has also been described from other glaciers: Findelengletscher (Reference Iken, and Bindschadler,Iken and Bindschadler, 1986) and Variegated Glacier (Reference Kamb, and Engelhart,Kamb and Engelhart, 1987). In the case of Findelengletscher, the close relationship between the two parameters was attributed to hydraulic jacking in cavities at the bed. The empirical relationships obtained from the velocity and water-pressure data from Findelengletscher and Storglaciären are similar in form, although the surface velocities on Findelengletscher are an order of magnitude higher. This implies that the processes governing the flow of the two glaciers must also he similar. Subglacial till is found to be deforming continuously underneath Storglaciären (Reference Iverson,, Hanson,, Hooke, and Jansson,Iverson and others, in press) and so cannot explain the variations in surface speed. It is thus inferred that the velocity variations here too are caused by hydraulic jacking.
Acknowledgements
I am deeply indebted to R. Hooke for all his encouragement, support, and comments regarding this work. Critical comments were provided by Dr Ν. Humphrey and one anonymous reviewer. Dr A. Iken read an early version of the manuscript and made many useful points. Numerous people at the Tarfala Research Station have helped in collecting the data through the years, sincere thanks are due for their combined efforts without which this project would not have been possible. Financial support has been graciously given by The Swedish Society for Anthropology and Geography, The Ahlmann Fund, The Swedish Touring Club Fund for Scientific Research, the Helge Ax:son Johnson Foundation, The Gertrude and Ivar Philipson Foundation, The Royal Swedish Academy of Sciences, The Lagrelius Fund the Ograduerades Fund, and the U.S. National Science Foundation (grants DPP-8414190 and DPP-8619086).