Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gazaki, Evangelia
2016.
The local symbol complex of a reciprocity functor.
Annals of K-Theory,
Vol. 1,
Issue. 3,
p.
317.
Rülling, Kay
Sugiyama, Rin
and
Yamazaki, Takao
2022.
Tensor structures in the theory of modulus presheaves with transfers.
Mathematische Zeitschrift,
Vol. 300,
Issue. 1,
p.
929.

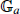 and abelian varieties
and abelian varieties