Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mondal, Arkapal
Parikh, Sarthak
Pradhan, Pulak
and
Sengar, Ritu
2025.
Toward holography on biregular trees.
Physical Review D,
Vol. 112,
Issue. 8,

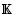 ), where
), where 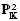 ,ℤ)
,ℤ)