Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T07:42:24.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of local grain boundary strengthening utilizing the extrinsic indentation size effect

Published online by Cambridge University Press:  14 May 2019

Prasad Pramod Soman ,
Erik G. Herbert ,
Katerina E. Aifantis  and
Stephen A. Hackney
Prasad Pramod Soman
Affiliation:
Department of Materials Science and Engineering, Michigan Technological University, Houghton, Michigan 49931, USA
Erik G. Herbert
Affiliation:
Department of Materials Science and Engineering, Michigan Technological University, Houghton, Michigan 49931, USA
Katerina E. Aifantis*
Affiliation:
Mechanical and Aerospace Engineering, University of Florida, Gainesville, Florida 32612, USA
Stephen A. Hackney*
Affiliation:
Department of Materials Science and Engineering, Michigan Technological University, Houghton, Michigan 49931, USA
*
a)Address all correspondence to these authors. e-mail: kaifantis@ufl.edu
b)e-mail: hackney@mtu.edu
Get access

Abstract

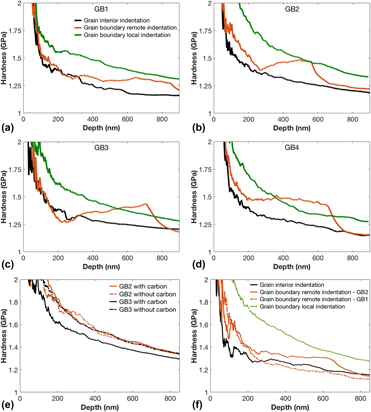
The extrinsic indentation size effect (ISE) is utilized to analyze the depth-dependent hardness for Berkovich indentation of non-uniform dislocation distributions with one and two dimensional deformation gradients and is then extended to indentation results at grain boundaries. The role of the Berkovich pyramid orientation and placement relative to the grain boundary on extrinsic ISE is considered in terms of slip transmission at yield and plastic incompatibility during post-yield deformation. The results are interpreted using a local dislocation hardening mechanism originally proposed by Ashby, combined with the Hall–Petch equation. The Hall–Petch coefficient determined from the extrinsic ISE of the grain boundary is found to be consistent with the published values for pure Fe and mild steel. A simple, linear continuum strain gradient plasticity model is used to further analyze the results to include contributions from a non-uniform distribution in plastic strain and dislocation density.

Keywords

nano-indentationhardnessgrain boundaries
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 13: Focus Issue: Intrinsic and Extrinsic Size Effects in Materials , 15 July 2019 , pp. 2347 - 2369
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

c)

This author was an editor of this journal during the review and decision stage. For the JMR policy on review and publication of manuscripts authored by editors, please refer to http://www.mrs.org/editor-manuscripts/.

References

Nix, W.D. and Gao, H.: Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 46, 411 (1998).CrossRefGoogle Scholar
Ngan, A.H.W. and Ng, H.P.: Indentation-induced damage of thin-films supported on substrates. In Advances in Fracture Research—10th International Congress on Fracture (Pergamon, Oxford, 2001).Google Scholar
Ashby, M.F.: The deformation of plastically non-homogeneous materials. Philos. Mag. 21, 399 (1970).CrossRefGoogle Scholar
Durst, F.K., Backes, B., and Goken, M.: Indentation size effect in metallic materials: Correcting for the size of the plastic zone. Scr. Mater. 52, 1093 (2005).CrossRefGoogle Scholar
Hou, X.D., Bushby, A.J., and Jennett, N.M.: Study of the interaction between the indentation size effect and Hall–Petch effect with spherical indenters on annealed polycrystalline copper. J. Phys. D: Appl. Phys. 41 (2008).CrossRefGoogle Scholar
Voyiadjis, G.Z. and Yaghoobi, M.: Review of nanoindentation size effect: Experiments and atomistic simulation. Crystals 7, 321 (2017).CrossRefGoogle Scholar
Wang, Z.: Influences of sample preparation on the indentation size effect and nanoindentation pop-in on nickel. Ph.D. dissertation, University of Tennessee, Knoxville, 2012. Available at: https://trace.tennessee.edu/utk_graddiss/1371.Google Scholar
Pharr, G.M., Herbert, E.G., and Gao, Y.: The indentation size effect: A critical examination of experimental observations and mechanistic interpretations. Annu. Rev. Mater. Res. 40, 271 (2010).CrossRefGoogle Scholar
McElhaney, K.W., Vlassak, J.J., and Nix, W.D.: Determination of indenter tip geometry and indentation contact area for depth-sensing indentation experiments. J. Mater. Res. 13, 1300 (1998).CrossRefGoogle Scholar
Liu, Y. and Ngan, A.H.W.: Depth dependence of hardness in copper single crystals measured by nanoindentation. Scr. Mater. 44, 237 (2001).CrossRefGoogle Scholar
Poole, W., Ashby, M.F., and Fleck, N.A.: Micro-hardness of annealed and work hardened Cu polycrystals. Scr. Mater. 4, 559–564 (1996).CrossRefGoogle Scholar
Backes, B., Huang, Y., Goken, M., and Durst, K.: The correlation between the internal material length scale and the microstructure in nanoindentation experiments and simulations using the conventional mechanism-based strain gradient plasticity theory. J. Mater. Res. 24, 1197 (2009).CrossRefGoogle Scholar
Soman, P.P., Herbert, E.G., Aifantis, K.E., and Hackney, S.A.: Effect of processing on Nix–Gao bilinear indentation results obtained for high purity iron. MRS Adv. 3, 477 (2018).CrossRefGoogle Scholar
Rester, M., Motz, C., and Pippan, R.: Microstructural investigation of the volume beneath nanoindentations in copper. Acta Mater. 55, 6427 (2007).CrossRefGoogle Scholar
Jung, B-b., Lee, H-k., and Park, H-c.: Effect of grain size on the indentation hardness for polycrystalline materials by the modified strain gradient theory. Int. J. Solids Struct. 50, 2719 (2013).CrossRefGoogle Scholar
Aifantis, K.E. and Ngan, A.H.W.: Modeling dislocation-grain boundary interactions through gradient plasticity and nanoindentation. Mater. Sci. Eng., A 459, 251 (2007).CrossRefGoogle Scholar
Soer, W.A., Aifantis, K.E., and Hosson, J.T.M.D.: Incipient plasticity during nanoindentation at grain boundaries in body-centered cubic metals. Acta Mater. 53, 4665 (2005).CrossRefGoogle Scholar
Aifantis, K.E., Deng, H., Shibata, H., Tsurekawa, H., Lejcek, S., and Hackney, S.A.: Interpreting slip transmission through mechanically induced interface energies: A Fe–3% Si case study. J. Mater. Sci. 54, 1831 (2019).Google Scholar
Taylor, G.: Plastic strain in metals. J. Inst. Met. 62, 307 (1938).Google Scholar
Vachhani, S.J., Doherty, R.D., and Kalidindi, S.R.: Studies of grain boundary regions in deformed polycrystalline aluminum using spherical nanoindentation. Int. J. Plast. 81, 87 (2016).CrossRefGoogle Scholar
Yang, B. and Vehoff, H.: Dependence of nanohardness upon indentation size and grain size—A local examination of the interaction between dislocations and grain boundaries. Acta Mater. 55, 849 (2007).CrossRefGoogle Scholar
Xiao, X., Terentyev, D., Chen, Q., Yua, L., Chen, L., Bakaev, A., and Duan, H.: The depth dependent hardness of bicrystals with dislocation transmission through grain boundaries: A theoretical model. Int. J. Plast. 90, 212 (2017).CrossRefGoogle Scholar
Pathak, S., Michler, J., and Wasmer, K.: Studying grain boundary regions in polycrystalline materials using spherical nano-indentation and orientation imaging microscopy. J. Mater. Sci. 47, 815 (2012).CrossRefGoogle Scholar
Aifantis, E.C.: On the microstructural origin of certain inelastic models. J. Eng. Mater. Technol. 106, 326 (1984).CrossRefGoogle Scholar
Fleck, N.A., Muller, G.M., Ashby, M.F., and Hutchinson, J.W.: Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 42, 475 (1994).CrossRefGoogle Scholar
Aifantis, E.C.: Exploring the applicability of gradient elasticity to certain micro/nano reliability problems. Microsyst. Technol. 15, 109 (2009).CrossRefGoogle Scholar
Aifantis, K.E. and Willis, J.R.: Interfacial jump conditions in strain-gradient plasticity and relations of Hall–Petch type. In Proceedings of the Seventh U. S. National Congress of Applied Mechanics (June 24–26 Chania/Greece) (2004); p. 372.Google Scholar
Aifantis, K.E. and Willis, J.R.: The role of interfaces in enhancing the yield strength of composites and polycrystals. J. Mech. Phys. Solids 53, 1047 (2005).CrossRefGoogle Scholar
Rogers, H.C.: The influence of hydrogen on the yield point in Fe. Acta Metall. 4, 114–117 (1956).CrossRefGoogle Scholar
Song, E.J., Suh, D-W., and Bhadeshia, H.K.D.H.: Theory for hydrogen desorption in ferritic steel. Comput. Mater. Sci. 39, 36–44 (2013).CrossRefGoogle Scholar
Lucas, B.N.: An Experimental Investigation of Creep and Viscoelastic Properties Using Depth Sensing Indentation Techniques, Materials Science and Engineering (University of Tennessee, Knoxville, 1997).Google Scholar
Pharr, G.M., Strader, J.H., and Oliver, W.C.: Critical issues in making small-depth mechanical property measurements by nanoindentation with continuous stiffness measurement. J. Mater. Res. 24, 653–666 (2009).CrossRefGoogle Scholar
Merle, B., Maier-Kiener, V., and Pharr, G.M.: Influence of modulus-to-hardness ratio and harmonic parameters on continuous stiffness measurement during nanoindentation. Acta Mater. 134, 167–176 (2017).CrossRefGoogle Scholar
Herbert, E.G., Hackney, S.A., Dudney, N.J., and Phani, P.S.: Nanoindentation of high purity vapor deposited lithium films: The elastic modulus. J. Mater. Res. 33, 1335–1346 (2018).CrossRefGoogle Scholar
Herbert, E.G., Sudharshan, P., and Johanns, K.E.: Nanoindentation of viscoelastic solids: A critical assessment of experimental methods. Curr. Opin. Solid State Mater. Sci. 19, 334–339 (2015).CrossRefGoogle Scholar
Oliver, W.C. and Pharr, G.M.: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564–1583 (1992).CrossRefGoogle Scholar
Herbert, E.G., Hackney, S.A., Dudney, N.J., Thole, V., and Phani, P.S.: Nanoindentation of high purity vapor deposited lithium films: A mechanistic rationalization of diffusion-mediated flow. J. Mater. Res. 33, 1347–1360 (2018).CrossRefGoogle Scholar
Samuels, L.E.: The nature of mechanically polished metal surfaces: The surface deformation produced by the abrasion and polishing of 70: 30 brass. J. Inst. Met. 85, 51 (1956).Google Scholar
Wilkinson, A.J. and Randman, D.: Determination of elastic strain fields and geometrically necessary dislocation distributions near nanoindents using electron back scatter diffraction. Philos. Mag. 90, 1159–1177 (2010).CrossRefGoogle Scholar
Ruggles, T.: Characterization of geometrically necessary dislocation content with EBSD-based continuum dislocation microscopy. ProQuest Dissertation and Theses, Brigham Young University, Provo, Utah, 4392, 2015.Google Scholar
Remington, T.P., Ruestes, C.J., Bringa, E.M., Remington, B.A., Lu, C.H., Kad, B., and Meyers, M.A.: Plastic deformation in nanoindentation of tantalum: A new mechanism for prismatic loop formation. Acta Mater. 78, 378–393 (2014).CrossRefGoogle Scholar
Nes, E.: Recovery revisited. Acta Metall. Mater. 43, 2189 (1995).CrossRefGoogle Scholar
Britton, T., Randman, D., and Wilkinson, A.: Nanoindentation study of slip transfer phenomenon at grain boundaries. J. Mater. Res. 24, 607 (2009).CrossRefGoogle Scholar
Armstrong, R.W., Codd, I., Douthwaite, R.M., and Petch, N.J.: The plastic deformation of polycrystalline aggregates. Philos. Mag. 7, 4558 (1962).CrossRefGoogle Scholar
Hall, E.O.: The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. B 64, 747 (1951).CrossRefGoogle Scholar
Petch, N.: The cleavage strength of polycrystals. J. Iron Steel Inst. 174, 25 (1953).Google Scholar
Hansen, N.: The effect of grain size and strain on the tensile flow stress of aluminium at room temperature. Acta Metall. 25, 863 (1977).CrossRefGoogle Scholar
Evers, L.P., Parks, D.M., Brekelmans, W.A.M., and Geers, M.G.D.: Crystal plasticity model with enhanced hardening by geometrically necessary dislocation accumulation. J. Mech. Phys. Solids 50, 2403 (2002).CrossRefGoogle Scholar
Wierzbanowski, K., Baczmanski, A., Lipinski, P., and Lodini, A.: Arch. Metall. Mater. 52, 77 (2007).Google Scholar
Ma, A. and Hartmaier, A.: On the influence of isotropic and kinematic hardening caused by strain gradients on the deformation behaviour of polycrystals. Philos. Mag. 94, 125 (2014).CrossRefGoogle Scholar
Li, J.C.M.: Petch relation and grain boundary sources. Trans. Metall. Soc. AIME 227, 239 (1963).Google Scholar
Meakin, J. and Petch, N.J.: Report ASD-TDR-63-324, Symposium on the Role of Substructure in the Mechanical Behavior of Metals (ASD-7DR-63-324, Orlando, 1963); pp. 234–251.Google Scholar
Kato, M.: Hall–Petch relationship and dislocation model for deformation of ultrafine-Grained and nanocrystalline metals. Mater. Trans. 55, 19–24 (2014).CrossRefGoogle Scholar
Conrad, H., Feuerstein, S., and Rice, L.: Effects of grain size on the dislocation density and flow stress of niobium. Mater. Sci. Eng. 2, 157–168 (1967).CrossRefGoogle Scholar
Conrad, H.: Effect of grain size on the lower yield and flow stress of iron and steel. Acta Metall. 11, 75 (1963).CrossRefGoogle Scholar
Kocks, U.F.: Metall. Trans. 1, 1123 (1970).Google Scholar
Takeda, K., Nakada, N., Tsuchiyama, T., and Takaki, S.: Effect of interstitial elements on Hall–Petch coefficient of ferritic iron. ISIJ Int. 48, 1122 (2008).CrossRefGoogle Scholar
Wei, X., Konstantinidis, A., Qi, C., and Aifantis, E.: Gradient plasticity used for modeling extrinsic and intrinsic size effects in the torsion of Au microwires. J. Mech. Behav. Mater. 25, 53 (2016).CrossRefGoogle Scholar
Evans, A.G. and Hutchinson, J.W.: A critical assessment of theories of strain gradient plasticity. Acta Mater. 57, 1675 (2009).CrossRefGoogle Scholar
Zhang, X. and Aifantis, K.E.: Examining the evolution of the internal length as a function of plastic strain. Mater. Sci. Eng., A 631, 27 (2015).CrossRefGoogle Scholar
Feng, G. and Nix, W.D.: Indentation size effect in MgO. Scr. Mater. 51, 599 (2004).CrossRefGoogle Scholar
Aifantis, K.E. and Willis, J.R.: Scale effects induced by strain-gradient plasticity and interfacial resistance in periodic and randomly heterogeneous media. Mech. Mater. 38, 702 (2006).CrossRefGoogle Scholar
Sachs, G.: Zur Ableitung einer Fließbedingung. Z. Ver. Deutscher Ing. 72, 734 (1928).Google Scholar
Mokios, G. and Aifantis, E.C.: Gradient effects in micro-/nanoindentation. Mater. Sci. Technol. 28, 1072 (2012).CrossRefGoogle Scholar
Stoelken, J.S. and Evans, A.G.: A microbend test method for measuring the plasticity length scale. Acta Mater. 46, 5109 (1998).CrossRefGoogle Scholar
Niordson, C.F. and Hutchinson, J.W.: Basic strain gradient plasticity theories with application to constrained film deformation. J. Mech. Mater. Struct. 6, 395 (2011).CrossRefGoogle Scholar
Engelen, R.A.B.: Plasticity-induced Damage in Metals: Nonlocal Modelling at Finite Strains (Technische Universiteit Eindhoven, Eindhoven, 2005).Google Scholar