Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T13:34:35.189Z Has data issue: false hasContentIssue false
  • English
  • Français

A mechanical reduced order model for elastomeric 3D printed architectures

Published online by Cambridge University Press:  21 January 2018

Todd H. Weisgraber ,
Thomas Metz ,
Christopher M. Spadaccini ,
Eric B. Duoss ,
Ward Small ,
Jeremy M. Lenhardt ,
Robert S. Maxwell  and
Thomas S. Wilson
Todd H. Weisgraber*
Affiliation:
Materials Engineering Division, Lawrence Livermore National Laboratory, Livermore, California 94550, USA
Thomas Metz
Affiliation:
Materials Engineering Division, Lawrence Livermore National Laboratory, Livermore, California 94550, USA
Christopher M. Spadaccini
Affiliation:
Materials Engineering Division, Lawrence Livermore National Laboratory, Livermore, California 94550, USA
Eric B. Duoss
Affiliation:
Materials Engineering Division, Lawrence Livermore National Laboratory, Livermore, California 94550, USA
Ward Small
Affiliation:
Materials Science Division, Lawrence Livermore National Laboratory, Livermore, California 94550, USA
Jeremy M. Lenhardt
Affiliation:
Materials Science Division, Lawrence Livermore National Laboratory, Livermore, California 94550, USA
Robert S. Maxwell
Affiliation:
Materials Science Division, Lawrence Livermore National Laboratory, Livermore, California 94550, USA
Thomas S. Wilson
Affiliation:
Materials Science Division, Lawrence Livermore National Laboratory, Livermore, California 94550, USA
*
a)Address all correspondence to this author. e-mail: weisgraber2@llnl.gov
Get access

Abstract

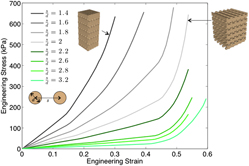
Direct ink writing of silicone elastomers enables printing with precise control of porosity and mechanical properties of ordered cellular solids, suitable for shock absorption and stress mitigation applications. With the ability to manipulate structure and feedstock stiffness, the design space becomes challenging to parse to obtain a solution producing a desired mechanical response. Here, we derive an analytical design approach for a specific architecture. Results from finite element simulations and quasi-static mechanical tests of two different parallel strand architectures were analyzed to understand the structure-property relationships under uniaxial compression. Combining effective stiffness-density scaling with least squares optimization of the stress responses yielded general response curves parameterized by resin modulus and strand spacing. An analytical expression of these curves serves as a reduced order model, which, when optimized, provides a rapid design capability for filament-based 3D printed structures. As a demonstration, the optimal design of a face-centered tetragonal architecture is computed that satisfies prescribed minimum and maximum load constraints.

Keywords

cellular (material form)stress/strain relationshipelastic properties
Type
Invited Articles
Information
Journal of Materials Research , Volume 33 , Issue 3: Focus Issue: Architected Materials , 14 February 2018 , pp. 309 - 316
Check for updates
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

b)

This author was an editor of this journal during the review and decision stage. For the JMR policy on review and publication of manuscripts authored by editors, please refer to http://www.mrs.org/editor-manuscripts/.

Contributing Editor: Katia Bertoldi

References

REFERENCES

Truby, R.L. and Lewis, J.A.: Printing soft matter in three dimensions. Nature 540, 371 (2016).Google Scholar
King, W.E., Anderson, A.T., Ferencz, R.M., Hodge, N.E., Kamath, C., Khairallah, S.A., and Rubenchik, A.M.: Laser powder bed fusion additive manufacturing of metals; physics, computational, and materials challenges. Appl. Phys. Rev. 2, 041304 (2015).Google Scholar
Lewis, J.A.: Direct ink writing of 3D functional materials. Adv. Funct. Mater. 16, 2193 (2006).Google Scholar
Duoss, E.B., Weisgraber, T.H., Hearon, K., Zhu, C., Small, W., Metz, T.R., Vericella, J.J., Barth, H.D., Kuntz, J.D., Maxwell, R.S., Spadaccini, C.M., and Wilson, T.S.: Three-dimensional printing of elastomeric, cellular architectures with negative stiffness. Adv. Funct. Mater. 24, 4905 (2014).CrossRefGoogle Scholar
Maiti, A., Small, W., Lewicki, J.P., Weisgraber, T.H., Duoss, E.B., Chinn, S.C., Pearson, M.A., Spadaccini, C.M., Maxwell, R.S., and Wilson, T.S.: 3D printed cellular solid outperforms traditional stochastic foam in long-term mechanical response. Sci. Rep. 6, 24871 (2016).Google Scholar
Zheng, X., Lee, H., Weisgraber, T.H., Shusteff, M., DeOtte, J., Duoss, E.B., Kuntz, J.D., Biener, M.M., Ge, Q., Jackson, J.A., Kucheyev, S.O., Fang, N.X., and Spadaccini, C.M.: Ultralight, ultrastiff mechanical metamaterials. Science 344, 1373 (2014).CrossRefGoogle ScholarPubMed
Meza, L.R., Zelhofer, A.J., Clarke, N., Mateos, A.J., Kochmann, D.M., and Greer, J.R.: Resilient 3D hierarchical architected metamaterials. Proc. Natl. Acad. Sci. U. S. A. 112, 11502 (2015).Google Scholar
Wang, Q., Jackson, J.A., Ge, Q., Hopkins, J.B., Spadaccini, C.M., and Fang, N.X.: Lightweight mechanical metamaterials with tunable negative thermal expansion. Phys. Rev. Lett. 117, 175901 (2016).Google Scholar
Liu, J., Gu, T., Shan, S., Kang, S.H., Weaver, J.C., and Bertoldi, K.: Harnessing buckling to design architected materials that exhibit effective negative swelling. Adv. Mater. 28, 6619 (2016).Google Scholar
Gladman, A.S., Matsumoto, E.A., Nuzzo, R.G., Mahadevan, L., and Lewis, J.A.: Biomimetic 4D printing. Nat. Mater. 15, 413 (2016).CrossRefGoogle Scholar
Wu, A.S., Small, W. IV, Bryson, T.M., Cheng, E., Metz, T.R., Schulze, S.E., Duoss, E.B., and Wilson, T.S.: 3D printed silicones with shape memory. Sci. Rep. 7, 4664 (2017).Google Scholar
Lode, A., Meyer, M., Brüggemeier, S., Paul, B., Baltzer, H., Schropfer, M., Winkelmann, C., Sonntag, F., and Gelinsky, M.: Additive manufacturing of collagen scaffolds by three-dimensional plotting of highly viscous dispersions. Biofabrication 8, 015015 (2016).CrossRefGoogle ScholarPubMed
Mrozek, R.A., Gold, C.S., Leighliter, B., Sietins, J.M., and Lenhart, J.L.: Open pore, elastomeric scaffolds through frustrated particle collapse. J. Mater. Sci. 51, 10761 (2016).CrossRefGoogle Scholar
Mac Murray, B.C., An, X., Robinson, S.S., van Meerbeek, I.M., O’Brien, K.W., Zhao, H., and Shepherd, R.F.: Poroelastic foams for simple fabrication of complex soft robots. Adv. Mater. 27, 6334 (2015).Google Scholar
Bendsoe, M.P. and Sigmund, O.: Topology Optimization (Springer Science & Business Media, Berlin, Heidelberg, 2013).Google Scholar
Valdevit, L., Godfrey, S.W., Schaedler, T.A., Jacobsen, A.J., and Carter, W.B.: Compressive strength of hollow microlattices: Experimental characterization, modeling, and optimal design. J. Mater. Res. 28, 2461 (2013).CrossRefGoogle Scholar
Messner, M.C.: Optimal lattice-structured materials. J. Mech. Phys. Solids 96, 162 (2016).CrossRefGoogle Scholar
Watts, S. and Tortorelli, D.A.: A geometric projection method for designing three-dimensional open lattices with inverse homogenization. Int. J. Numer. Meth. Eng. 60, 351 (2017).Google Scholar
Zheng, Q., Jiang, D., Huang, C., Shang, X., and Ju, S.: Analysis of failure loads and optimal design of composite lattice cylinder under axial compression. Compos. Struct. 131, 885 (2015).CrossRefGoogle Scholar
Weickum, G., Eldred, M.S., and Maute, K.: A multi-point reduced-order modeling approach of transient structural dynamics with application to robust design optimization. Struct. Multidiscipl. Optim. 38, 599 (2008).Google Scholar
Puso, M.A.: NIKE3D: A nonlinear, implicit, three-dimensional finite element code for solid and structural mechanics - User's Manual (Lawrence Livermore National Laboratory, Livermore, California, 2012).Google Scholar
Gibson, L.J. and Ashby, M.F.: Cellular Solids, Structure and Properties (Cambridge University Press, Cambridge, U. K., 1999).Google Scholar
Worsley, M.A., Kucheyev, S.O., Satcher, J.H. Jr., Hamza, A.V., and Baumann, T.F.: Mechanically robust and electrically conductive carbon nanotube foams. Appl. Phys. Lett. 94, 073115 (2009).Google Scholar
Ogden, R.W.: Recent advances in the phenomenological theory of rubber elasticity. Rubber Chem. Technol. 59, 361 (1986).CrossRefGoogle Scholar
Hill, R.: Advances in Applied Mechanics, Vol. 18 (Elsevier, Cambridge, Massachusetts, 1979); pp. 1–75.Google Scholar
Finkel, D.E. and Kelley, C.: Convergence analysis of the direct algorithm. Optim. Online 14, 1 (2004).Google Scholar