A number of errors in typesetting have been discovered in Tseng (Reference Tseng2014), for which the Editor-in-Chief of The Journal of Navigation and Cambridge University Press apologise.
The following corrections to Tseng (Reference Tseng2014) are made for Volume 67 Issue 5, Pages 825–844:
Page 827, in the line following Equation (5) replace ![]() $\tan \beta _V = \sqrt {1 - c^2 /c}\, $ with
$\tan \beta _V = \sqrt {1 - c^2 /c}\, $ with ![]() $\tan \beta _V = \sqrt {1 - c^2} /c$.
$\tan \beta _V = \sqrt {1 - c^2} /c$.
Page 828, in the line following Equation (7) replace symbol “u” with symbol “μ” in two expressions (![]() $u = \sqrt {1 - c^2 - x^2} $ and σ=arctan(x/u)).
$u = \sqrt {1 - c^2 - x^2} $ and σ=arctan(x/u)).
Page 832, Figure 6: units should be added (degree ° for β V and minute ′ for A.R.).
Page 832, in the line following Equation (20) replace symbol “u” with symbol “μ” in two expressions and replace expression (having wrong signs) β V⩽β⩽−β V with correction − β V⩽β i⩽β V, i=1,2.
Page 835, in Equation (29) replace “0 ⩽ β 12 ⩽π” with “0 ⩽ λ 12 ⩽ π”.
Page 835, in the paragraph following Equation (29) replace the sign (<=) in expression λ 12 <=(1− f)π with the sign (⩽), the expression becomes a appropriate expression (λ 12⩽(1− f)π).
Page 836, in Equation (32):
replace expression ![]() $NS = \left\{\!{\matrix{1,\cr 0,\cr}}\right.\matrix{{(\lambda_{12} - \Delta \lambda _{NS} ) \gt 0} \cr {(\lambda _{12} - \Delta \lambda _{NS} ) \lt 0} \cr} $ with
$NS = \left\{\!{\matrix{1,\cr 0,\cr}}\right.\matrix{{(\lambda_{12} - \Delta \lambda _{NS} ) \gt 0} \cr {(\lambda _{12} - \Delta \lambda _{NS} ) \lt 0} \cr} $ with ![]() $NS = \left\{\!{\matrix{1, \cr 0, \cr}} \right.\matrix{ {(\lambda _{12} - \lambda _{NS} ) \gt 0} \cr {(\lambda _{12} - \lambda _{NS} ) \lt 0} \cr} $.
$NS = \left\{\!{\matrix{1, \cr 0, \cr}} \right.\matrix{ {(\lambda _{12} - \lambda _{NS} ) \gt 0} \cr {(\lambda _{12} - \lambda _{NS} ) \lt 0} \cr} $.
Page 837, in Equation (41) replace the equation
![]() $\tan \beta _V = \sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12} /\sin \lambda _{12}} $ with
$\tan \beta _V = \sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12} /\sin \lambda _{12}} $ with ![]() $\tan \beta _V = \sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12}} /\hskip-1pt\sin \lambda _{12} $
$\tan \beta _V = \sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12}} /\hskip-1pt\sin \lambda _{12} $
Page 837, in Equation (42) replace the equation
![]() $c = \cos \beta _V = \sin \lambda _{12} /\sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12} + \sin \lambda _{12}} $ with
$c = \cos \beta _V = \sin \lambda _{12} /\sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12} + \sin \lambda _{12}} $ with ![]() $c = \cos \beta _V = \sin \lambda _{12} /\sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12} + \sin ^2 \lambda _{12}} $
$c = \cos \beta _V = \sin \lambda _{12} /\sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12} + \sin ^2 \lambda _{12}} $
Page 837, in Equation (43) replace the equation ![]() $\pi \sqrt {1 - e^2 \lt \lambda _{12} \leqslant \pi} $ with
$\pi \sqrt {1 - e^2 \lt \lambda _{12} \leqslant \pi} $ with ![]() $\pi \sqrt {1 - e^2} \lt \lambda _{12} \leqslant \pi $.
$\pi \sqrt {1 - e^2} \lt \lambda _{12} \leqslant \pi $.
Page 838, in second paragraph after Equation (47) replace “asteroid” with “astroid”.
Page 839, in third box from top in Figure 7 replace illogical expression |β 1 + β 2|< eps with |β 1|+|β 2|<eps.
Page 839, in fourth box from top in Figure 7 replace the expression
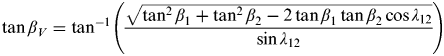 $\tan \beta _V = \tan ^{ - 1} \left(\displaystyle{{\sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12}}} \over {\sin \lambda _{12}}}\right)$ with
$\tan \beta _V = \tan ^{ - 1} \left(\displaystyle{{\sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12}}} \over {\sin \lambda _{12}}}\right)$ with
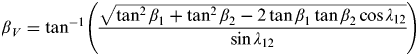 $\beta _V = \tan ^{ - 1} \left(\displaystyle{{\sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12}}} \over {\sin \lambda _{12}}}\right)$ and
$\beta _V = \tan ^{ - 1} \left(\displaystyle{{\sqrt {\tan ^2 \beta _1 + \tan ^2 \beta _2 - 2\tan \beta _1 \tan \beta _2 \cos \lambda _{12}}} \over {\sin \lambda _{12}}}\right)$ and
replace NS = IIF (λ NS > 0,1,0) with NS = IIF (λ 12−λ NS > 0,1,0).
Page 840, in bottom paragraph replace the statement “The geodesic is slightly more curved than the great ellipse (see Figure 9).” with: “In the Mercator projection, the geodesic appears to be slightly more curved than the great ellipse (see Figure 9).”
Page 841, in Tables 1 and 2, column 1 replace typos “Karny” with “Karney”.
Page 843, in Reference Clairaut (1735) replace “perpendiculaireà” by “perpendiculaire à”.
Page 844, Reference Karney (2013) replace “43–42” with “43–55”.
Page 844, Reference Thomas and Featherstone (2005) replace typo “formual” with “formula”.

