1. INTRODUCTION
When a maritime navigator takes a sight of a celestial body it results in a Line of Position (LoP) on the surface of the Earth on which the ship's true position could lie. A second sight then fixes the position at the intersection of the two LoPs. In practice, due to limitations on the accuracy with which altitudes can be measured, the actual position lies within a band of uncertainty on either side of the LoPs with a probability that decreases as the perpendicular distance from the LoP increases. For this reason and to serve as an indication of the quality of the sights, it is common practice when possible to take at least one more. Ideally the three LoPs should meet at a single point but in practice they will form a triangle that in navigational parlance is referred to as the cocked hat.
The question of the likelihood that the cocked hat encloses the observer's true position has been examined by Williams (Reference Williams1991) who gave the answer as 25%. For three LoPs the derivation requires no complex mathematics but hinges solely on there being an equal chance that the true position falls on either side of any given LoP. The result had actually been known for a long time (Admiralty Navigation Manual, 1938, Vol. III, P.166). It is a special case of a more general result given by Daniels (Reference Daniels1951) that for n LoPs the probability of the observer's true position being inside the largest closed polygon that they form is 
$\overline {\Pr } \lpar {\hbox{in}} \rpar =1-n/2^{n-1}$. Williams’ article generated considerable follow up discussion (Lee, Reference Lee1991; Gething, Reference Gething1992; Swift, Reference Swift1992; Cook, Reference Cook1993). More recently Kaplan (Reference Kaplan2019) has investigated this topic using Monte Carlo methods.
The importance of understanding the exact question to which an answer has been found has been emphasised elsewhere (Adams, Reference Adams1979). As Cook (Reference Cook1993) pointed out:
‘The probabilities that we seek should be thought of as the probability that, for example, a random cocked hat will enclose the (fixed) true position, which may be unknown to the observer, but may, of course, be known to some outside agency. It should not be thought of as the probability that, having obtained a particular cocked hat, the true position is inside.’
to which Williams responded:
‘but the probabilities associated with the particular cocked hat which we happen to have is precisely the question I addressed.’
In the case where the three LoPs of the particular cocked hat meet at a point the probability of being inside is zero and not 25% and he is therefore mistaken. By giving simple counter-examples using binary probability distributions, Cook further demonstrated that the fixed probabilities given by Williams for regions external to the triangle are erroneous and that they depend on the actual error distribution. Unfortunately, the topic was closed at that point.
In this paper the problem of the probabilities associated with the cocked hat is revisited with the aim of obtaining closed form analytic expressions when the errors in the observed altitudes are assumed to be normally distributed. Azimuths are taken to be fixed. The question as to the probability that the observer's true position falls inside the cocked hat, or in regions bounded by the LoPs outside, can be asked before any sights are made and the size and shape of the cocked hat is yet to be determined. This will be referred to as the a priori problem and is what Cook is describing in the quotation above. The question can also be asked once a round of sights has actually been taken and the realised geometry of the cocked hat is known. This will be referred as the a posteriori problem. In this case, the probability of the position falling inside this particular cocked hat, or regions outside, depends on the distribution of the observational errors. However, if an ensemble of observers, each subject to the same random errors, took simultaneous sights from the same location of the same three bodies, the average of the a posteriori probabilities for the true position to be inside the cocked hat would approach 25%. In this paper the a posteriori probabilities are integrated analytically to obtain expressions for the corresponding a priori averages.
There is a natural tendency to regard a small cocked hat as indicating a round of high quality sights. That it does, but it does not indicate a correspondingly high probability that the cocked hat encloses the observer's true position. Indeed, the smaller the area of the cocked hat the lower the probability of falling inside. It is natural to focus on the visible triangle drawn on the chart or plotting sheet but what the LoPs are doing is defining an elliptical probability distribution of where the observer's true position might lie as is shown in Figure 2. The maximum of the distribution lies at a point inside the cocked hat. For a given set of standard deviations and azimuths, a smaller cocked hat means a tighter more concentrated probability distribution. This, in turn implies smaller uncertainties on the observer's location but not a higher probability of being inside the cocked hat. This may initially seem counterintuitive to some. Having obtained a set of three sights the results in this paper allow the navigator to calculate the probability that their true position falls within that cocked hat or in any of the exterior regions bounded by the LoPs. The assumption is made that the errors in altitude, or their equivalents, follow a normal or Gaussian distribution as is widely done in literature (Daniels, Reference Daniels1951; DiDonato et al., Reference DiDonato, Jarnagin and Hageman1980; DiDonato and Hageman, Reference DiDonato and Hageman1982; Kaplan, Reference Kaplan2019; Stansfield, Reference Stansfield1947). If the true error distribution differs from a Gaussian, the results given here will be less than exact but provided it is centrally peaked and symmetrical about its mean, the values obtained should still provide meaningful estimates.
Section 2 lays out the notation and conventions used and Section 3 derives some geometric properties of the cocked hat that are relevant to the problem at hand. Expressions for the a posteriori and a priori average probabilities are derived in Section 4. Appendix A gives the definition and properties of the Bivariate Cumulative Normal function along with some of its integrals that are necessary for finding a priori averages. Appendix B generalises the expressions for the a posteriori probabilities to an arbitrary number of LoPs. Appendix C gives expressions for the properties of confidence ellipses in the presence of an arbitrary number of LoPs.
2. NOTATION AND CONVENTIONS
For the purposes of this analysis the standard Cartesian coordinate system will be adopted. Positive values on the x and y axes will be identified as lying to the observer's east and north respectively. Azimuthal angles, Z, will be measured clockwise from the y axis or equivalently from north in an easterly direction.
Each celestial sight, if free from error, results in a Line of Position (LoP) along which the observer's position must lie. Each LoP is specified by an intercept, r, and azimuth, Z, measured from an arbitrary, but generally conveniently chosen reference point referred to as the Assumed Position (AP). If 
$\vec{p}$ is the point on the LoP nearest to the AP then the intercept, r, and azimuth, Z, are its distance and bearing from the AP respectively. In other words, r is the perpendicular distance of the LoP from the AP and the direction Z is at right angles to the direction of the LoP itself. The standard Cartesian coordinates x and y representing the horizontal and vertical directions, respectively, will be used throughout. In a navigational context these are the Departure (Dep.) and Latitude Difference (D.Lat.) from the AP.
The intercept, r, is determined by measuring the altitude of a celestial body by means of a sextant or similar device and is subject to a random error that will be assumed to be drawn from a normal distribution with zero mean and standard deviation, σ. This induces an uncertainty in the observer's position that is normally distributed at right angles to the LoP. The LoP is thus surrounded by a band of uncertainty. If the standard deviation in the altitude measurement is σ minutes of arc then standard deviation of this error band is σ Nautical Miles (NM).
Figure 1 shows a contour plot of the probability density function for the observer's true position as determined from a single LoP indicated by the black line. Darker shades indicate lower probability. Figure 2 shows the probability density function for the observer's true position as determined from the three LoPs that form the cocked hat. Its peak is indicated and is known as the Maximum Probability Point or Most Probable Position (MPP). At the MPP the sum of the squares of the perpendicular distances to the LoPs is minimum and it always lies inside the cocked hat. It is known as the symmedian point of the triangle. The contours shown in Figure 2 are ellipses of constant probability density known as Confidence Ellipses. The contours remain ellipses for more than three LoPs. Compact general expressions for the position of the centre, directions of the principal axes and dimensions of the elliptical contours for an arbitrary number of LoPs are given in Appendix C.
Figure 1. Probability density function for the observer's true position generated by a single LoP.
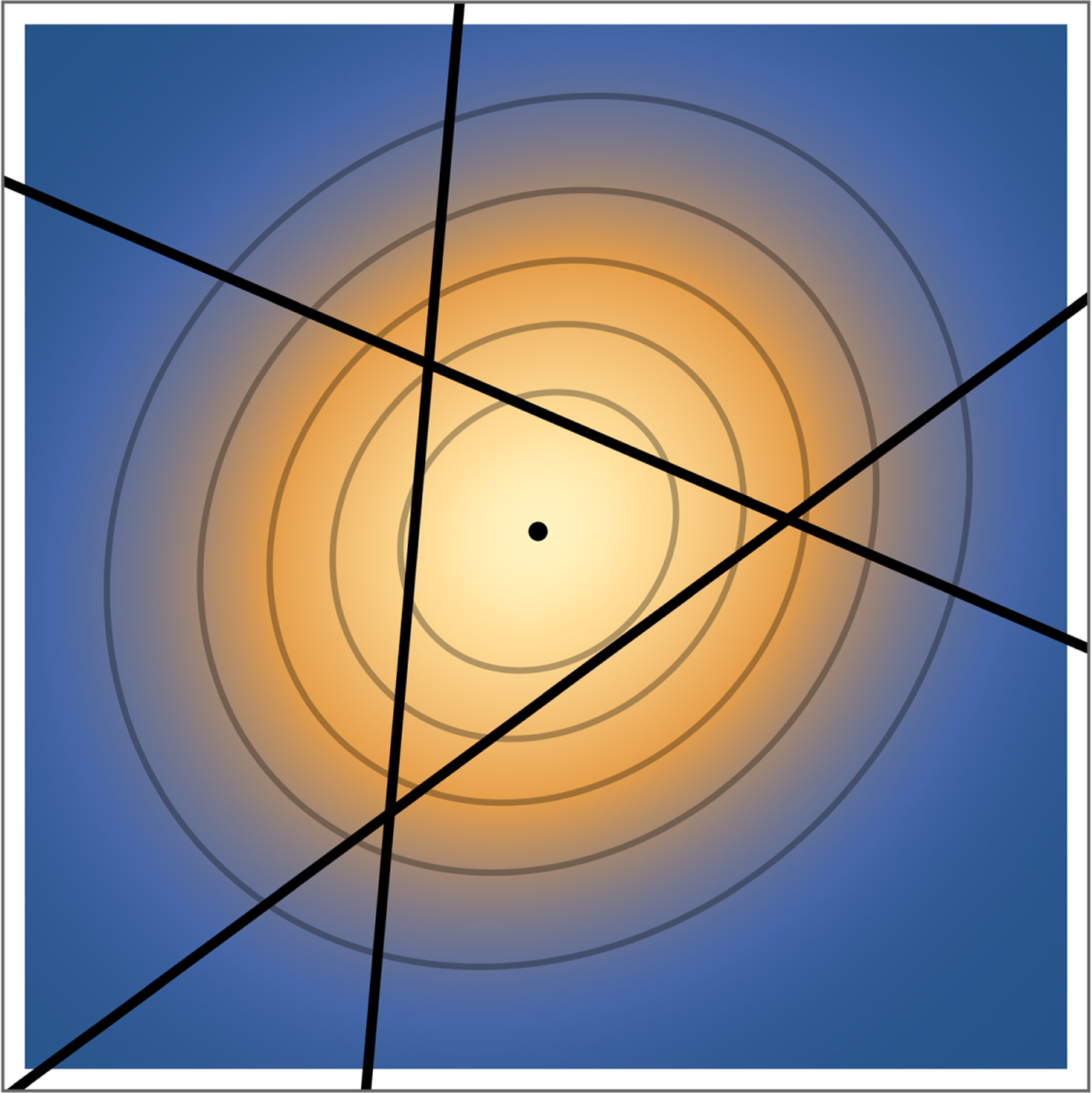
Figure 2. Probability density function for the observer's true position generated by three LoPs that form a cocked hat. The point marked at the centre is the symmedian point of the triangle or MPP. The plotted contours define confidence ellipses for the observer's true position.
In the real world, an LoP is a local approximation of a circle of position on a roughly spherical Earth. The results presented in this work are valid within the accuracy of this approximation.
Suppose three sets of sights have been taken yielding intercepts and azimuths, r i, Z i, for i=1, 2, 3. For convenience but not necessity, the index, i, will be assigned to the observations according to their azimuths consecutively in an anti-clockwise direction around the AP. As a consequence, each of the differences Z 1−Z 2, Z 2−Z 3 and Z 3−Z 1, can be taken to be positive. The LoPs will correspondingly be denoted LoPi, for i=1, 2, 3.
In most situations it would be expected that the standard deviations, σ i, associated with the error for each of the LoPs would be the same but for generality, here they will be maintained as distinct.
It is convenient to define the following quantities:
$$s_1 =\sigma _1^2 \sin^2 \lpar Z_2 -Z_3 \rpar ; \quad s_2 = \sigma_2^2 \sin^2 \lpar Z_3 -Z_1 \rpar ;\quad s_3 = \sigma_3^2 \sin \lpar {Z_1 -Z_2 } \rpar $$
$$A = s_1 + s_2 +s_3$$
$$B=r_1 \sin \lpar Z_2 -Z_3 \rpar + r_2 \sin \lpar Z_3 -Z_1 \rpar + r_3 \sin \lpar Z_1 -Z_2 \rpar $$3. GEOMETRY OF THE COCKED HAT
It is an exercise in simple coordinate geometry to show that the perpendicular distance of a point 
$\vec{p} = \lpar x,y \rpar $ from LoPi is:
$$d_i \lpar {x,y} \rpar =\vert {x\sin Z_i +y\cos Z_i -r_i } \vert $$and the LoPs themselves satisfy the equations:
$$x\sin Z_i + y \cos Z_i - r_i =0$$
The intersections of the LoPs form the vertices of the cocked hat. By solving pairs of simultaneous equations from Equation (5), the vertex, 
$\vec {v}_{ij}$, at intersection of LoPi and LoPj is found to be:
$$\vec {v}_{ij} =\hbox{csc} \lpar {Z_i -Z_j } \rpar \lpar {r_i \cos Z_j -r_j \cos Z_i ,r_j \sin Z_i -r_i \sin Z_j } \rpar $$
The area of the cocked hat may then be found by computing 
$\displaystyle{1 \over 2}\vert {\lpar {\vec {v}_{13} -\vec {v}_{12} } \rpar \times \lpar {\vec {v}_{23} -\vec {v}_{12} } \rpar } \vert $ which gives:
$$\hbox{Area}=\displaystyle{1 \over 2}\vert {\hbox{ csc } \lpar {Z_2 -Z_3 } \rpar \hbox{ csc } \lpar {Z_3 -Z_1 } \rpar \hbox{ csc } \lpar {Z_1 -Z_2 } \rpar } \vert B^2$$Equation (7) indicates that the quantity, B, is a property of the size and shape of the cocked hat alone and is independent of the choice of AP. This can be explicitly demonstrated as follows. Perform a translation to a new coordinate system x→x−x 0, y→y−y 0. In this coordinate system the LoP Equation (5) becomes:
$$x \sin Z_i +y\cos Z_i -\lpar {r_i +x_0 \sin Z_i +y_0 \cos Z_i } \rpar =0$$which is equivalent to the substitution:
$$r_i \to r_i +x_0 \sin Z_i +y_0 \cos Z_i.$$When this substitution is made in Equation (3) the result is found to be independent of x 0 and y 0.
By appealing to the properties of trilinear coordinates (Whitworth, Reference Whitworth1866. Ch. II) it can be shown that B = Area/R where R is the radius of the triangle's circumcircle.
4. COCKED HAT PROBABILITIES
In this section a proof is given for the 25% average probability along the lines of Williams’ (Reference Williams1991) argument but couched in terms of intercepts and azimuths rather than sides of the LoPs. Closed form expressions for the probabilities associated with a specific a posteriori or realised cocked hat are derived in terms of the Standard Bivariate Cumulative Normal function. It is shown by explicit calculation that when these expressions are weighted by the probability of a particular cocked hat actually occurring and integrated over all possible configurations, the 25% a priori average probability is recovered. Expressions for the corresponding probabilities in exterior regions are also obtained.
In the development given here, averages are taken over the intercepts, r i, only. The azimuth angles Z i are taken as being fixed. This is reflective of a reality in which the azimuths are dictated by the celestial bodies available for the sights.
4.1. Average a priori probability
Assume the observer's true position is at the origin, 
$\vec{0}=\lpar {0,0} \rpar $. Observations yield a cocked hat with vertices at the points 
$\vec {v}_{ij} $as given in Equation (6). A point 
$\vec{p}$ is interior to the triangle if when expressed as the linear combination of the vertex points:
$$\lambda \vec {v}_{23} +\mu \vec {v}_{13} +\lpar {1-\lambda -\mu} \rpar \vec {v}_{12} =\vec {p}$$
the coefficients satisfy the conditions 0<λ, μ, (1 − λ − μ) < 1. Applying Equation (10) to the origin, 
$\vec{0}$, and solving for λ and μ these conditions become:
$$0 \lt \displaystyle{r_1 \sin \lpar {Z_2 -Z_3 } \rpar \over B},\displaystyle{r_2 \sin \lpar {Z_3 -Z_1 } \rpar \over B},\displaystyle{r_3 \sin \lpar {Z_1 -Z_2 } \rpar \over B} \lt 1$$As the azimuths, Z i, are labelled sequentially in an anti-clockwise direction, at most one of the Z 2−Z 3, Z 3−Z 1, Z 1−Z 2 is greater than 180° and hence at most one of their sines is negative. To determine the probability that the origin lies inside the triangle two cases need to be considered.
1. All sines are positive: Conditions for the origin to lie inside the triangle will be satisfied if all the r i are either positive or negative. If the probability distribution for the r i has a median of zero then the probability for this is 1/4 in agreement with Williams (Reference Williams1991).
2. One of the sines is negative: For definiteness take sin(Z 2−Z 3)< 0. Conditions for the origin to lie inside the triangle will be satisfied if r 1< 0 and r 2, r 3>0 or if r 1> 0 and r 2, r 3< 0. Again, if the probability distribution for the r i has a median of zero then the probability for this happening is 1/4.
4.2. A posteriori probability
In this section an expression is derived for the probability that the observer's true position falls inside the cocked hat formed from a specific set of sights. By its very definition the result cannot depend on the probability of the specific sights being realised and it will be seen in the final analysis that this requirement is in fact satisfied.
For a given set of three celestial sights the probability that the observer's true location lies in an infinitesimal area, dxdy, located at the point (x, y) is:
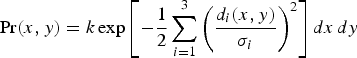$$\Pr \lpar {x,y} \rpar = k \exp \left[ -\displaystyle{1 \over 2}\sum\limits_{i=1}^3 \left(\displaystyle{d_i \lpar {x,y} \rpar \over \sigma_i} \right)^2 \right]dx\,dy$$where k is a normalisation factor found by requiring that the integral of Pr(x,y) over the entire plane is 1. The required probability of interest here is obtained by integrating the probability density function over the triangular region bounded by the three LoPs. However, instead of calculating this directly, the probability of being outside the triangle will be calculated by dividing the area into three sectors. The sum will then be subtracted from 1 to obtain the desired result. A similar approach was adopted for numerical evaluations over arbitrary polygons (DiDonato et al., Reference DiDonato, Jarnagin and Hageman1980; DiDonato and Hageman, Reference DiDonato and Hageman1982).
Figure 3 shows the cocked hat generated by the observations in Table 1.
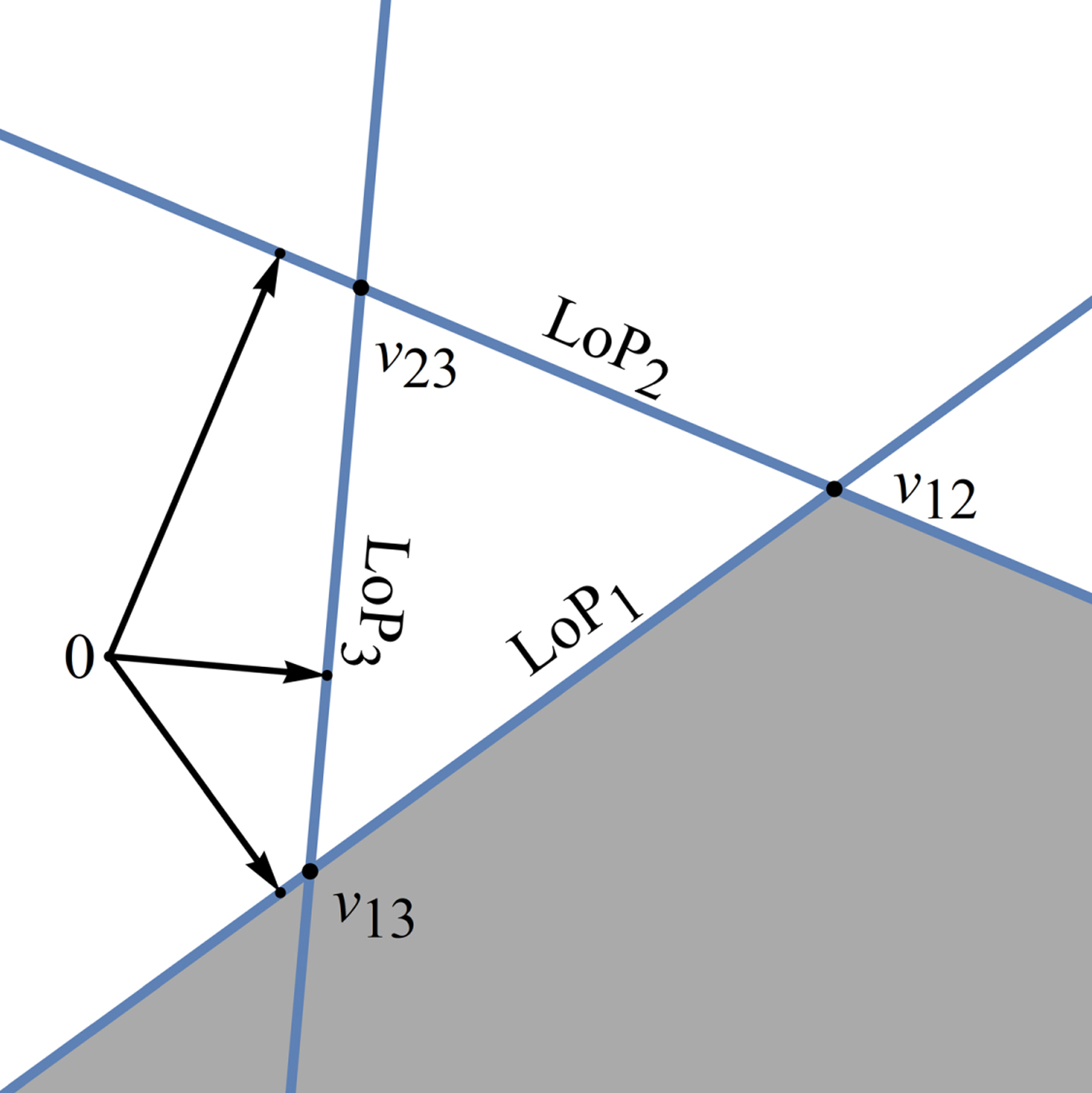
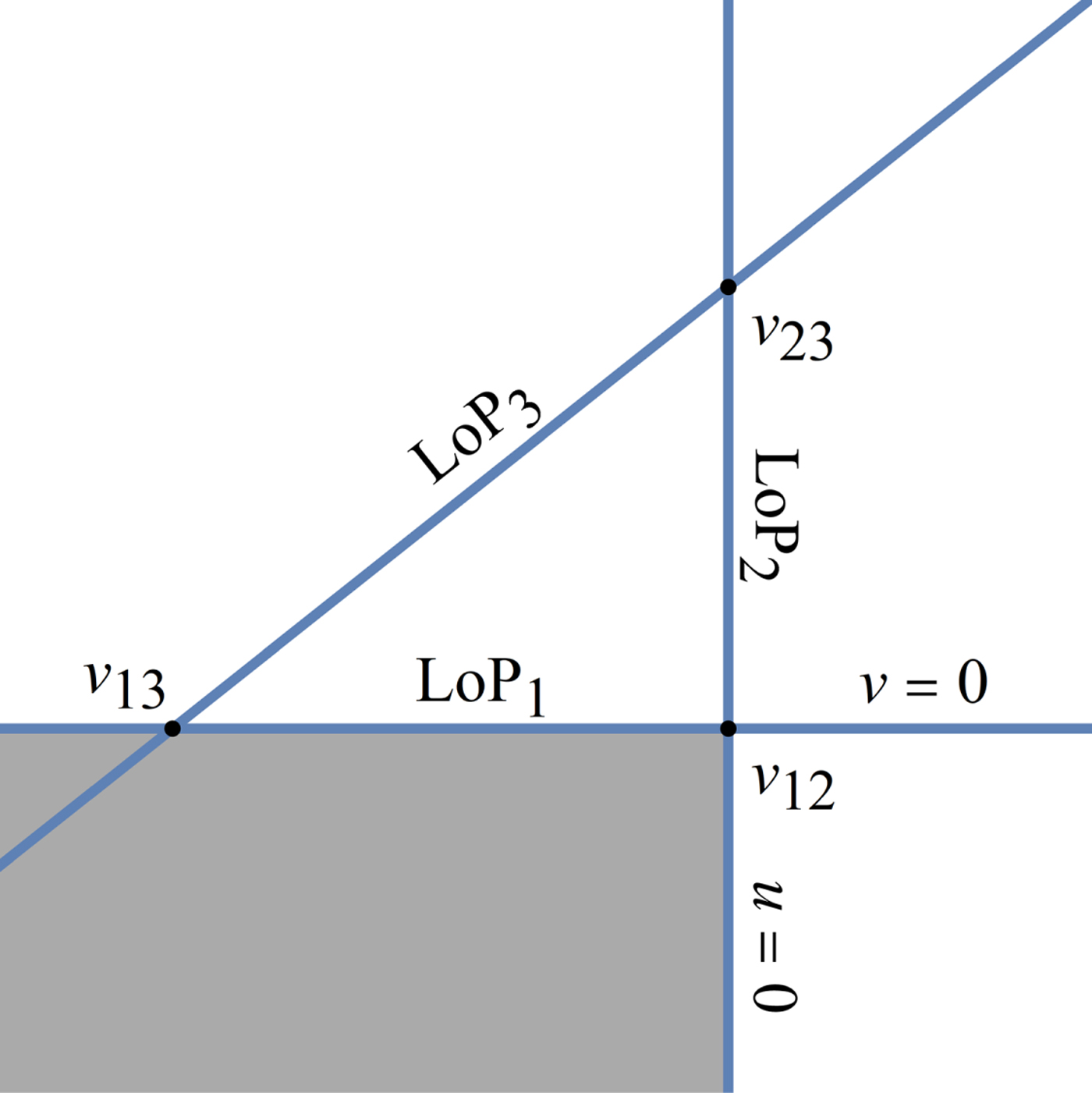
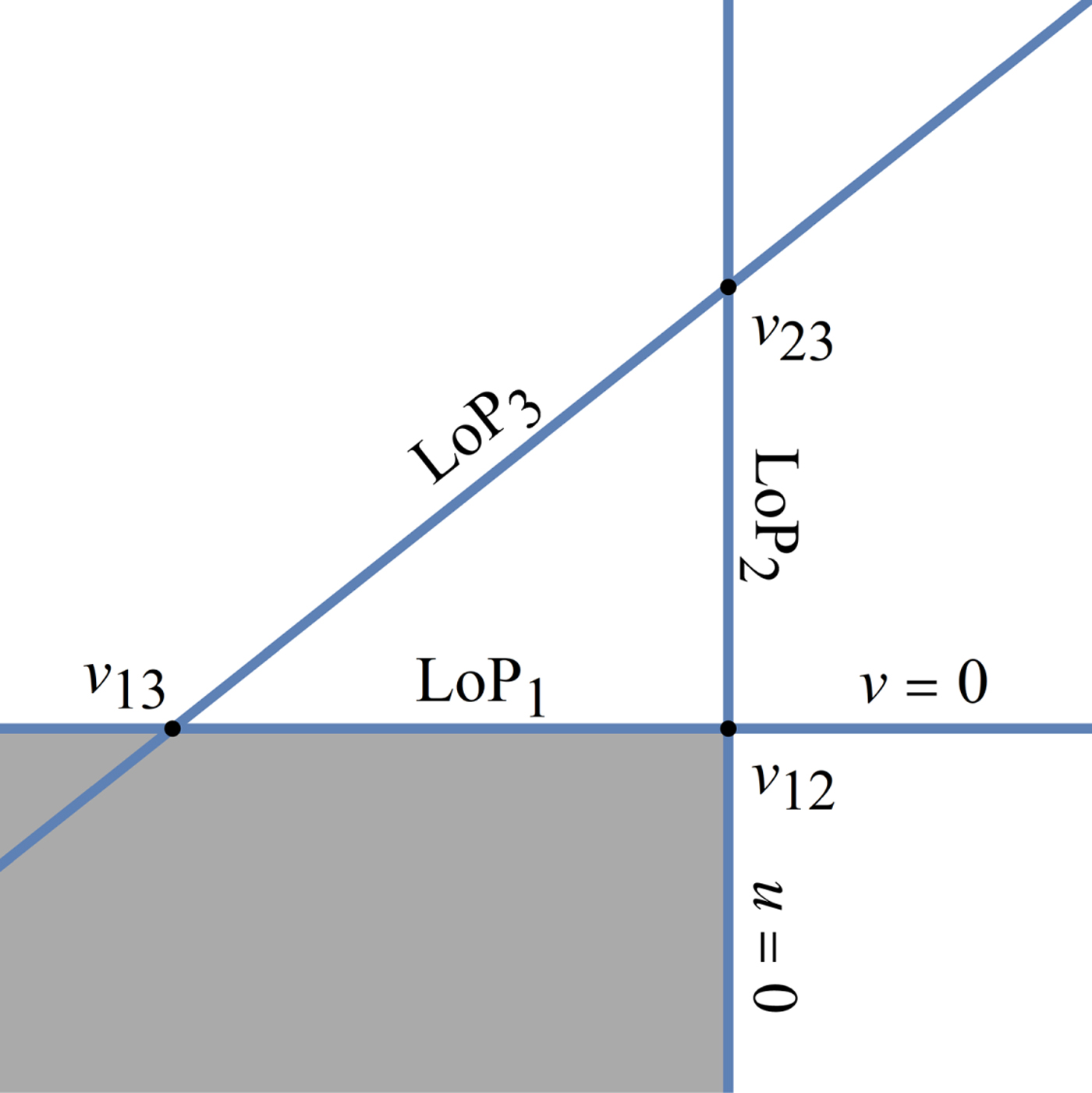
Figure 3. Cocked hat on the x-y plane produced by three LoPs. The grey region borders LoP1 on the opposite side of the line from the triangle and LoP2 on the same side of the triangle.
Table 1. Observations for example calculation.
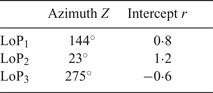
The area shaded in grey is specified by being bounded by LoP1 on the opposite side from the triangle and by LoP2 on same side as the triangle. Together with areas constructed in the same way for LoP2, LoP3 and LoP3, LoP1 these three disjoint sectors cover the entire plane outside of the triangle.
The integral over the shaded area can be expressed in terms of the Standard Bivariate Cumulative Normal function, Φ2(x, y; ρ), whose properties are summarised in Appendix A. In order to achieve this, a linear transform that maps the shaded region into the third quadrant is applied as shown in Figure 4. Since the LoPs satisfy Equation (5), the transformations:
$$\eqalign{u&=\eta \lpar x \sin Z_2 + y \cos Z_2 -r_2 \rpar \cr v &= \xi \lpar x \sin Z_1 + y \cos Z_1 -r_1 \rpar }$$map LoP1 to the u axis and LoP2 to the v axis. The multipliers η and ξ will be used to track the overall sign of the transformation and it is assumed that η2 = ξ2 = 1. Under this transformation the triangle vertices map to the following images on the u−v plane:
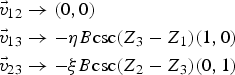$$\eqalign{&\vec{v}_{12} \to \lpar {0,0} \rpar \cr &\vec {v}_{13} \to -\eta B\hbox{csc} \lpar {Z_3 -Z_1} \rpar \lpar {1,0} \rpar \cr &\vec{v}_{23} \to -\xi B \hbox{csc} \lpar {Z_2 -Z_3} \rpar \lpar {0,1} \rpar }$$ In order ensure that the shaded region falls on the specified sides of LoP1 and LoP2 relative to the triangle, the image of the vertex point 
$\vec {v}_{13} $ must lie on the negative horizontal u-axis and the image of 
$\vec {v}_{23}$ must lie on the positive vertical v-axis. These requirements can be imposed by the appropriate choices of ξ and η, or explicitly:
$$\eta = \hbox{sgn}\lpar {B\hbox{ csc } \lpar {Z_3 -Z_1 } \rpar } \rpar ;\quad \xi =-\hbox{sgn}\lpar {B\hbox{ csc } \lpar {Z_2 -Z_3 } \rpar } \rpar $$Using Equation (A9) to perform the integral over the third quadrant of the u-v plane gives:
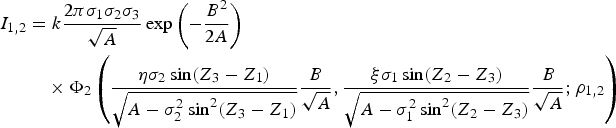$$\eqalign{I_{1,2} &= k\displaystyle{2\pi \sigma _1 \sigma _2 \sigma_3 \over \sqrt A} \exp \left( {-\displaystyle{B^2 \over 2A}} \right) \cr &\quad \times \Phi _2\left( {\displaystyle{\eta \sigma_2 \sin \lpar {Z_3 -Z_1 } \rpar \over \sqrt {A-\sigma_2^2 \sin^2\lpar {Z_3 -Z_1 } \rpar } }\displaystyle{B \over \sqrt A },\displaystyle{\xi \sigma_1 \sin \lpar {Z_2 -Z_3 } \rpar \over \sqrt {A-\sigma_1^2 \sin^2\lpar {Z_2 -Z_3 } \rpar } }\displaystyle{B \over \sqrt A };\rho_{1,2} } \right)}$$where:
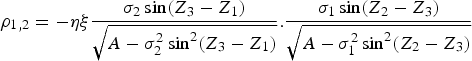$$\rho _{1,2} = -\eta \xi \displaystyle{\sigma _2 \sin \lpar {Z_3 -Z_1 } \rpar \over \sqrt {A-\sigma _2^2 \sin ^2\lpar {Z_3 -Z_1 } \rpar }}. \displaystyle{\sigma _1 \sin \lpar {Z_2 -Z_3 } \rpar \over \sqrt {A-\sigma _1^2 \sin ^2\lpar {Z_2 -Z_3 } \rpar }}$$Equation (A8) can also be used to obtain the integral over the entire u-v plane which yields the normalisation factor:
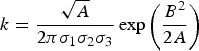$$k = \displaystyle{\sqrt A \over 2\pi \sigma _1 \sigma _2 \sigma _3 }\exp \left( {\displaystyle{B^2 \over 2A}} \right)$$ Define the quantities 
$f_{i} =\sqrt{s_{i}/(A-s_{i})}$. Then by inspecting the interactions among ξ, η and the quantities they multiply, and appealing to the symmetry of Φ2(x, y; ρ) in its arguments x, y yields the simple expression:
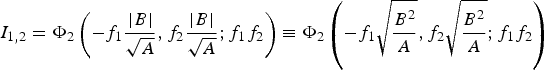$$I_{1,2} =\Phi _2 \left({-f_1 \displaystyle{\vert B \vert \over \sqrt{A}}, f_2 \displaystyle{\vert B \vert \over \sqrt{A}}; f_1 f_2} \right) \equiv \Phi _2 \left(-f_1 \sqrt{\displaystyle{B^2 \over A}}, f_2 \sqrt{\displaystyle{B^2 \over A}}; f_1 f_2 \right)$$For a given set of three sights, the probability that the observer's actual position falls within the cocked hat is:
$$\Pr (\hbox{in})=1-I_{1,2} -I_{2,3} -I_{3,1}$$As anticipated and because the intercepts, r i, enter only through the combination B, it follows as shown in Section 3 that the result depends on the geometric properties of the cocked hat but not its location relative to the AP.
It should be expected that the probability that the observer's true position is enclosed by the cocked hat decreases as its area gets smaller, tending to zero in the limit that the LoPs cross at a point or, equivalently from Equation (7), when B=0. This provides a useful check on the limiting behaviour of the result. From Equation (A8):
$$ {\Pr \lpar {\hbox{in}} \rpar } \vert _{B = 0} = \displaystyle{1 \over 4} - \displaystyle{1 \over 2\pi} \lpar \sin^{-1} f_1 f_2 + \sin^{-1} f_2 f_3 + \sin^{-1} f_1 f_3 \rpar .$$ Writing f if j = sinθij then the right-hand side of Equation (19) will vanish if 
$\theta_{12} + \theta_{23} + \theta _{13} =\displaystyle{\pi \over 2}$ or equivalently:
$$\sin \theta_{12} = \sin \left(\displaystyle{\pi \over 2} - \theta_{23} -\theta_{13} \right) = \cos \lpar \theta_{23} + \theta_{13} \rpar = \cos \theta_{23} \cos \theta_{13} -\sin \theta_{23} \sin \theta_{13}$$
This condition translates to 
$f_{1} f_{2} =\sqrt {1-f_{2}^{2} f_{3}^{2} } \sqrt {1-f_{1}^{2} f_{3}^{2} } -f_{1} f_{2} f_{3}^{2} $ which after some algebra can be shown to be satisfied.
4.3. Probabilities in other regions of the plane
Equation (17) gives the integral of the probability density function over the third (lower left) quadrant of the u-v plane shown in Figure 4. The integral over the fourth (lower right) quadrant can be obtained by changing the sign of η in the transformations Equation (13) which produces a reflection of Figure 4 in the vertical v axis. Similarly changing the sign of ξ produces a reflection about the u axis. Using Equation (15) as a guide, it follows that the probabilities for the four quadrants are related by changes in sign in the arguments of Φ2.
Define:
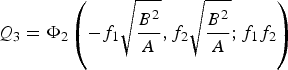$$Q_3 =\Phi _2 \left(-f_1 \sqrt{\displaystyle{B^2 \over A}}, f_2 \sqrt{\displaystyle{B^2 \over A}}; f_1 f_2 \right)$$and then by the symmetry properties Equations (A5) and (A6), the integrals in each of the four quadrants in Figure 4 are:
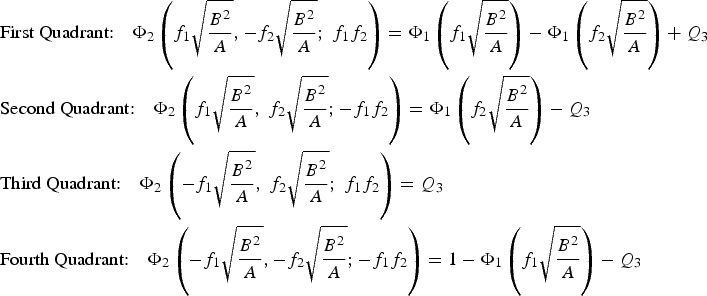$$\eqalign{&\hbox{First Quadrant:}\quad \Phi _2 \left( {f_1 \sqrt {\displaystyle{B^2 \over A}} ,-f_2 \sqrt {\displaystyle{B^2 \over A}} ;\ f_1 f_2 } \right)=\Phi _1 \left( {f_1 \sqrt {\displaystyle{B^2 \over A}} } \right)-\Phi _1 \left( {f_2 \sqrt {\displaystyle{B^2 \over A}} } \right)+Q_3 \cr &\hbox{Second Quadrant:}\quad \Phi _2 \left( {f_1 \sqrt {\displaystyle{B^2 \over A}} ,\ f_2 \sqrt {\displaystyle{B^2 \over A}} ; -f_1 f_2 } \right)=\Phi _1 \left( {f_2 \sqrt {\displaystyle{B^2 \over A}} } \right)-Q_3 \cr &\hbox{Third Quadrant:} \quad \Phi _2 \left( {-f_1 \sqrt {\displaystyle{B^2 \over A}} ,\ f_2 \sqrt {\displaystyle{B^2 \over A}} ;\ f_1 f_2 } \right)=Q_3 \cr &\hbox{Fourth Quadrant:} \quad \Phi _2 \left( {-f_1 \sqrt {\displaystyle{B^2 \over A}} ,-f_2 \sqrt {\displaystyle{B^2 \over A}} ;-f_1 f_2 } \right)=1-\Phi _1 \left( {f_1 \sqrt {\displaystyle{B^2 \over A}} } \right)-Q_3}$$Summing the expressions on the right-hand sides above gives 1 as expected. The results may be combined to deduce, for example, that the probability that the observer's position falling in the lower half plane is:
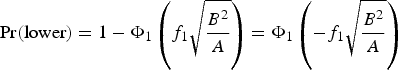$$\Pr \lpar {\hbox{lower}} \rpar = 1 - \Phi_1 \left(f_1 \sqrt{\displaystyle{B^2 \over A}} \right) = \Phi_1 \left(-f_1 \sqrt {\displaystyle{B^2 \over A}} \right)$$4.4. Relationship between the a priori and a posteriori probabilities
Summing together the probabilities that the observer's position is inside a particular cocked hat weighted by the probability of that cocked hat occurring gives the a priori average probability of falling inside. That is:
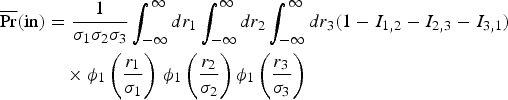$$\eqalign{\overline{\Pr} \lpar \hbox{in} \rpar & =\displaystyle{1 \over \sigma _1 \sigma _2 \sigma _3} \int_{-\infty }^{\infty} {dr_1 } \int_{-\infty }^\infty {dr_2 } \int_{-\infty }^\infty dr_3 \lpar {1-I_{1,2} -I_{2,3} -I_{3,1} } \rpar \cr &\quad \times \phi_1 \left(\displaystyle{r_1 \over \sigma_1} \right)\,\phi_1 \left(\displaystyle{r_2 \over \sigma_2} \right) \phi_1 \left(\displaystyle{r_3 \over \sigma_3} \right)}$$Since the intercepts, r i, only enter the functions I i, j through the combination B, it is convenient to eliminate r 3 in favour of B as a variable of integration and carry out the integrations in r 1 and r 2. Equation (23) then becomes:
$$\overline{\Pr} \lpar \hbox{in} \rpar = 1 - \int_{-\infty}^{\infty} \displaystyle{dB \over \sqrt A} \lpar I_{1,2} + I_{2,3} + I_{3,1} \rpar \,\phi_1 \left(\displaystyle{B\over \sqrt{A}} \right)$$ Note in passing that the technique used in going from Equation (23) to Equation (24) can be applied to obtain an expression for the average area of the cocked hat. Since: 
$\int_{-\infty }^{\infty} {dB\left( {{B^{2}} /{\sqrt A }} \right)\phi _{1} \left( {B /{\sqrt A }} \right)} =A$, it follows from Equation (7) that the average area is:
$$\overline{\hbox{Area}} = \displaystyle{1 \over 2}\vert {\hbox{csc} \lpar {Z_2 -Z_3 } \rpar \hbox{csc} \lpar {Z_3 -Z_1 } \rpar \hbox{csc} \lpar {Z_1 -Z_2 } \rpar } \vert A$$in agreement with Daniels (Reference Daniels1951). The quantity B 2/A that has appeared frequently in the foregoing can then be interpreted as the ratio of area of the cocked hat to the average area.
The integrals over B in Equation (24) can be found from Equation (A16). For the combinations of the arguments of Φ2 that occur here the last term on the right and side vanishes. Hence:
$$\int_{-\infty}^{\infty} \displaystyle{dB \over \sqrt{A}} I_{i,j} \,\phi _1 \left(\displaystyle{B \over \sqrt{A}} \right) = \displaystyle{1 \over 4} - \displaystyle{1 \over 2\pi} \tan^{-1} f_i + \displaystyle{1 \over 2\pi} \tan^{-1} f_j$$
and when substituted in Equation (24) the known result, 
$\overline {\Pr } \lpar {\hbox{in}} \rpar = \displaystyle{1 \over 4}$, is immediately recovered. Equation (A16) can also be applied to find the probabilities for the other quadrants in Figure 4. For example, in the case of the fourth quadrant in Figure 4 it is:
$$\Pr \lpar {Q_4} \rpar = \displaystyle{1 \over 4} - \displaystyle{1 \over 2\pi} \tan ^{-1}f_1 -\displaystyle{1 \over 2\pi} \tan^{-1} f_2$$Using standard trigonometric identities, the arctangents on the right-hand side of Equations (26) and (27) can be written in several equivalent ways:
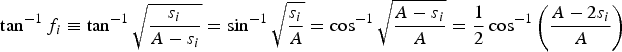$$\tan^{-1} f_i \equiv \tan^{-1} \sqrt{\displaystyle{s_i \over A-s_i}} = \sin^{-1} \sqrt{\displaystyle{s_i \over A}} =\cos^{-1} \sqrt{\displaystyle{A-s_i \over A}} =\displaystyle{1 \over 2} \cos^{-1} \left({\displaystyle{A-2s_i \over A}} \right)$$5. CONCLUSIONS
Compact closed form expressions for the probability of an observer's position falling inside and around a specific cocked hat have been derived assuming normally distributed measurement errors. Expressions have been given for integrals that involve the Standard Bivariate Cumulative Normal function and are used to explicitly demonstrate that for this case the average a priori probability of falling inside is indeed 25%. The results have been checked by generating cocked hats by Monte Carlo simulation and comparing the output of the analytic expressions to that of numerical integration using Mathematica.
Since the 25% average does not depend on the detailed statistical distribution of the errors, an analogous form to Equation (23) which evaluates to 1/4 must exist for any distribution having zero median. Understanding the mechanism by which this very general conclusion comes about might be a fruitful topic for future research.
ACKNOWLEDGEMENTS
The author wishes to thank George Kaplan for revisiting the problem of the cocked hat and for his encouragement to push this investigation to its conclusion.
APPENDIX A
A.1. STANDARD NORMAL AND STANDARD BIVARIATE NORMAL FUNCTION DEFINITIONS AND PROPERTIES
The Standard Normal function is defined as:
$$\phi_1 \lpar x \rpar = \displaystyle{1 \over \sqrt {2\pi}} \exp \left[-\displaystyle{x^2 \over 2} \right]$$and its integral is the Standard Cumulative Normal function:
$$\Phi_1 \lpar x \rpar = \displaystyle{1 \over \sqrt {2\pi}} \int_{-\infty}^x {du} \exp \left[-\displaystyle{u^2 \over 2} \right].$$The Standard Bivariate Normal function is:
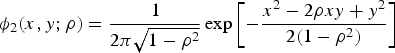$$\phi_2 \lpar x,y;\rho \rpar = \displaystyle{1 \over 2\pi \sqrt {1-\rho^2}} \exp \left[-\displaystyle{x^2-2\rho xy + y^2 \over 2\lpar 1-\rho^2 \rpar } \right]$$and the Standard Bivariate Cumulative Normal function is defined as:
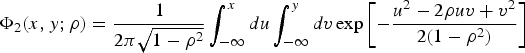$$\Phi_2 \lpar {x,y; \rho} \rpar = \displaystyle{1 \over 2\pi \sqrt{1-\rho ^2}} \int_{-\infty }^x {du} \int_{-\infty }^y {dv} \exp \left[ {-\displaystyle{u^2-2\rho uv+v^2 \over 2\lpar {1-\rho^2} \rpar }} \right]$$and is symmetric in its arguments x, y. A summary of its properties can be found in Abramowitz and Stegun (Reference Abramowitz and Stegun1964). A variety of methods have been devised for the numerical evaluation of this function, see Meyer (Reference Meyer2013) and references therein. It is also available as standard in a number of mathematical software packages.
The functions are normalised such that Φ1(∞) = Φ2(∞, ∞;ρ) = 1.
In this paper the following properties of Φ2 are used:
$$\Phi_2 \lpar {x,y;\rho } \rpar +\Phi _2 \lpar {-x,y;-\rho } \rpar =\Phi _1 \lpar y \rpar $$
$$\Phi_2 \lpar {x,y;\rho } \rpar -\Phi _2 \lpar {-x,-y;\rho } \rpar =\Phi _1 \lpar x \rpar +\Phi _1 \lpar y \rpar -1$$
$$\Phi _2 \lpar {\infty ,y;\rho } \rpar =\Phi _1 \lpar y \rpar $$
$$\Phi_2 \lpar {0,0;\rho } \rpar =\displaystyle{1 \over 4} + \displaystyle{\sin ^{-1}\rho \over 2\pi}$$ The general integral 
$\int_{-\infty}^{x} {du} \int_{-\infty}^{y} {dv} \exp [ -(au^{2} + buv + cv^{2} + du + ev + f)]$ can be expressed in terms of Φ2 by writing:
$$au^2+buv+cv^2+du+ev+f=a\lpar {u-m} \rpar ^2+b\lpar {u-m} \rpar \lpar {v-n} \rpar +c\lpar {v-n} \rpar ^2+p$$where:
$$m=\displaystyle{be-2cd \over 4ac-b^2};\quad n=\displaystyle{bd-2ae \over 4ac-b^2};\quad p = f - \displaystyle{ae^2-bde+cd^2 \over 4ac-b^2},$$and making the substitution u=x−m, v=y−n with the result:
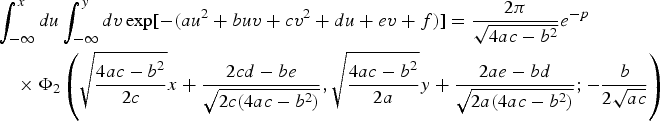$$\eqalign{&\int_{-\infty }^x {du} \int_{-\infty }^y {dv} \exp \lsqb {-\lpar {au^2+buv+cv^2+du+ev+f} \rpar } \rsqb = \displaystyle{2\pi \over \sqrt {4ac-b^2} }e^{-p} \cr &\quad\times \Phi _2\left( {\sqrt {\displaystyle{4ac-b^2 \over 2c}} x+\displaystyle{2cd-be \over \sqrt {2c\lpar {4ac-b^2} \rpar } },\sqrt {\displaystyle{4ac-b^2 \over 2a}} y+\displaystyle{2ae-bd \over \sqrt {2a\lpar {4ac-b^2} \rpar } };-\displaystyle{b \over 2\sqrt {ac} }} \right)}$$A.2. INTEGRALS OF THE STANDARD CUMULATIVE NORMAL AND STANDARD BIVARIATE CUMULATIVE NORMAL FUNCTIONS
As a preliminary, note that by transforming from Cartesian to polar coordinates it can be shown that (Gradshteyn and Rhyzhik, Reference Gradshteyn and Rhyzhik1965. 6.285):
$$\int_{-\infty }^\infty {\Phi _1 \lpar {\alpha \vert x \vert } \rpar \,} \phi _1 \left( {\displaystyle{x \over \sigma }} \right)\displaystyle{dx \over \sigma} = \displaystyle{1 \over \pi} \tan^{-1}\lpar {\alpha \sigma } \rpar +\displaystyle{1 \over 2}$$From Equations (A6) and (A10):
$$\int_0^\infty {\lsqb {\Phi_2 \lpar {\alpha \vert x \vert ,\beta \vert x \vert ;\rho } \rpar -\Phi_2 \lpar {-\alpha \vert x \vert ,-\beta \vert x \vert ;\rho } \rpar } \rsqb \,} \phi _1 \left( {\displaystyle{x \over \sigma}} \right)\displaystyle{dx \over \sigma} = \displaystyle{1 \over 2\pi }\tan ^{-1}\lpar {\alpha \sigma } \rpar +\displaystyle{1 \over 2\pi} \tan ^{-1}\lpar {\beta \sigma } \rpar $$To obtain expressions for the individual terms in the integrand separately note that:
$$\int_0^{\infty} {\lsqb {\Phi_2 \lpar {\alpha \vert x \vert ,\beta \vert x \vert ; \rho } \rpar +\Phi_2 \lpar {-\alpha \vert x \vert , - \beta \vert x \vert ; \rho } \rpar } \rsqb \,} \phi _1 \left( {\displaystyle{x \over \sigma}} \right)\displaystyle{dx \over \sigma} = \int_{-\infty }^\infty {\Phi _2 \lpar {\alpha x,\beta x;\rho } \rpar \,} \phi _1 \left( {\displaystyle{x \over \sigma}} \right)\displaystyle{dx \over \sigma }$$The integral on the right-hand side of Equation (A12) may be found by writing:
$$\int_{-\infty }^{\infty} {\Phi _2 \lpar {\alpha x,\beta x;\rho } \rpar \,} \phi _1 \left( {\displaystyle{x \over \sigma}} \right) \displaystyle{dx \over \sigma} = \int_{-\infty }^{\infty} {\displaystyle{dx \over \sigma}} \int_{-\infty }^0 {du} \int_{-\infty }^0 {dv} \,\phi _2 \lpar {u+\alpha x,v+\beta x;\rho } \rpar \phi _1 \left( {\displaystyle{x \over \sigma}} \right)$$The integrand is an exponential function of a quadratic in x which is easily integrated. Then the integral over u and v can be found using Equation (A9) which gives:
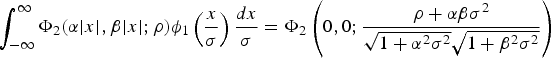$$\int_{-\infty }^{\infty} {\Phi _2 \lpar {\alpha \vert x \vert , \beta \vert x \vert ; \rho} \rpar } \phi _1 \left( {\displaystyle{x \over \sigma }} \right)\displaystyle{dx \over \sigma }=\Phi _2 \left( {0,0;\displaystyle{\rho +\alpha \beta \sigma^2 \over \sqrt {1+\alpha^2\sigma^2} \sqrt {1+\beta^2\sigma^2} }} \right)$$From Equation (A8) this is:
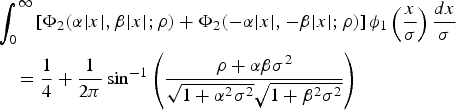$$\eqalign{&\int_0^{\infty} {\lsqb {\Phi_2 \lpar {\alpha \vert x \vert , \beta \vert x \vert ; \rho} \rpar + \Phi_2 \lpar {-\alpha \vert x \vert , - \beta \vert x \vert ; \rho } \rpar } \rsqb \,} \phi _1 \left( {\displaystyle{x \over \sigma }} \right)\displaystyle{dx \over \sigma } \cr &\quad =\displaystyle{1 \over 4}+\displaystyle{1 \over 2\pi}\sin ^{-1}\left( {\displaystyle{\rho +\alpha \beta \sigma^2 \over \sqrt {1+\alpha^2\sigma^2} \sqrt {1+\beta^2\sigma^2} }} \right)}$$which when combined with Equation (A11) gives the result:
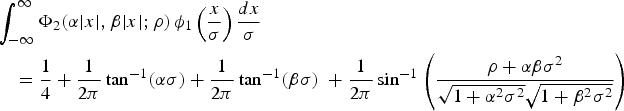$$\eqalign{&\int_{-\infty }^{\infty} {\Phi _2 \lpar {\alpha \vert x \vert , \beta \vert x \vert ; \rho} \rpar \,} \phi _1 \left( {\displaystyle{x \over \sigma }} \right) \displaystyle{dx \over \sigma} \cr &\quad = \displaystyle{1 \over 4} + \displaystyle{1 \over 2\pi} \tan^{-1} \lpar {\alpha \sigma} \rpar + \displaystyle{1 \over 2\pi} \tan^{-1} \lpar {\beta \sigma} \rpar \; + \displaystyle{1 \over 2\pi} \sin^{-1} \left(\displaystyle{\rho +\alpha \beta \sigma^2 \over \sqrt {1+\alpha^2\sigma^2} \sqrt {1+\beta^2\sigma^2} }\right)}$$APPENDIX B GENERALISATION TO MORE THAN THREE LINES OF POSITION
This paper considered the case of three LoPs which when plotted form a triangle. Greater numbers of LoPs form more complex polygons and calculating the probability that the observer's true position falls inside is correspondingly more complicated. With some extra effort the results obtained here can be generalised to treat this situation. DiDonato et al. (Reference DiDonato, Jarnagin and Hageman1980) and DiDonato and Hageman (Reference DiDonato and Hageman1982) describe procedures for numerically obtaining the integral of a bivariate normal probability density function over the interior of a polygon of arbitrary shape by dividing the exterior region into sectors in the same manner as used here for the cocked hat. Their procedure consists of two main steps. First, the appropriate exterior regions are identified and then the integral of the bivariate cumulative normal probability density function is performed numerically over those regions on a case by case basis. The generalisation of Equation (15) given in this appendix allows the numerical integration to be replaced by the convenient and efficient evaluation of a single standard function, Φ2. In Equation (15) LoP1 and LoP2 are bounding lines that define the region of integration and LoP3 just contributes to the integrand. When n LoPs are present LoP3 is replaced by a sum over n−2 LoPs and Equation (12) is integrated for a sum that runs from 1 to n. It is found that after the judicious application of trigonometric identities all required summations can be written using summands that involve a single term and are relatively simple in form.
Define:
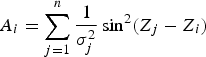$$A_i = \sum\limits_{j=1}^n {\displaystyle{1 \over \sigma _j^2 }} \sin ^2\lpar {Z_j -Z_i }\rpar $$
$$B_i = r_1 \sin \lpar {Z_2 -Z_i } \rpar +r_2 \sin \lpar {Z_i -Z_1 } \rpar +r_i \sin \lpar {Z_1 -Z_2 } \rpar .$$Note that B 1=B 2=0. After applying the transformations given in Equation (13) the quadratic coefficients in Equation (A9) are:
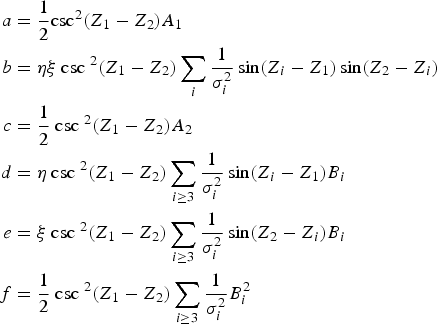$$\eqalign{a&=\displaystyle{1 \over 2}\hbox{csc}^2 \lpar {Z_1 -Z_2 } \rpar A_1 \cr b & =\eta \xi \hbox{ csc } ^2\lpar {Z_1 -Z_2 } \rpar \sum\limits_i {\displaystyle{1 \over \sigma _i^2 }\sin \lpar {Z_i -Z_1 } \rpar } \sin \lpar {Z_2 -Z_i } \rpar \cr c &=\displaystyle{1 \over 2}\hbox{ csc } ^2\lpar {Z_1 -Z_2 } \rpar A_2 \cr d&=\eta \hbox{ csc } ^2\lpar {Z_1 -Z_2 } \rpar \sum\limits_{i\ge 3} {\displaystyle{1 \over \sigma _i^2 }\sin \lpar {Z_i -Z_1 } \rpar } B_i \cr e&=\xi \hbox{ csc } ^2\lpar {Z_1 -Z_2 } \rpar \sum\limits_{i\ge 3} {\displaystyle{1 \over \sigma _i^2 }\sin \lpar {Z_2 -Z_i } \rpar } B_i \cr f&=\displaystyle{1 \over 2}\hbox{ csc } ^2\lpar {Z_1 -Z_2 } \rpar \sum\limits_{i\ge 3} {\displaystyle{1 \over \sigma _i^2 }} B_i^2}$$From these are obtained:
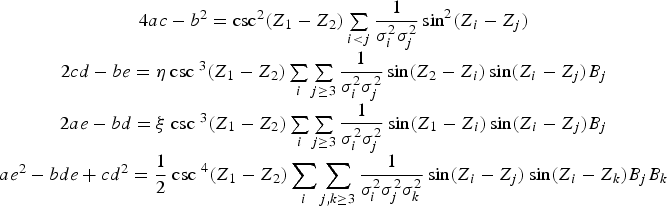$$\matrix{4ac-b^2=\hbox{csc}^2\lpar {Z_1 -Z_2 } \rpar \sum\limits_{i \lt j} {\displaystyle{1 \over \sigma _i^2 \sigma _j^2}} \sin ^2\lpar {Z_i -Z_j } \rpar \cr 2cd-be=\eta \hbox{ csc } ^3\lpar {Z_1 -Z_2 } \rpar \sum\limits_i {\sum\limits_{j\ge 3} {\displaystyle{1 \over \sigma _i^2 \sigma _j^2 }\sin \lpar {Z_2 -Z_i } \rpar } } \sin \lpar {Z_i -Z_j } \rpar B_j \cr 2ae-bd=\xi \hbox{ csc } ^3\lpar {Z_1 -Z_2 } \rpar \sum\limits_i {\sum\limits_{j\ge 3} {\displaystyle{1 \over \sigma _i^2 \sigma _j^2 }\sin \lpar {Z_1 -Z_i } \rpar } } \sin \lpar {Z_i -Z_j } \rpar B_j \cr ae^2-bde+cd^2=\displaystyle{1 \over 2}\hbox{ csc } ^4\lpar {Z_1 -Z_2 } \rpar \sum\limits_i {\sum\limits_{j,k\ge 3} {\displaystyle{1 \over \sigma _i^2 \sigma _j^2 \sigma _k^2 }\sin \lpar {Z_i -Z_j } \rpar \sin \lpar {Z_i -Z_k } \rpar } } B_j B_k}$$For n LoPs Equation (15) then becomes I 1,2 = Φ(x n, y n ;ρn) with:
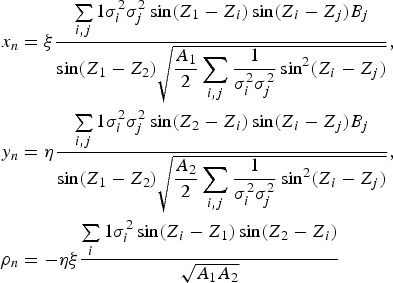$$\eqalign{x_n &=\xi \displaystyle{\sum\limits_{i,j} {\displaystyle{1}{\sigma _i^2 \sigma _j^2 }} \sin \lpar {Z_1 -Z_i } \rpar \sin \lpar {Z_i -Z_j } \rpar B_j \over \sin \lpar {Z_1 -Z_2 } \rpar \sqrt {\displaystyle{A_1 \over 2}\sum\limits_{i,j} {\displaystyle{1 \over \sigma _i^2 \sigma _j^2 }} \sin ^2\lpar {Z_i -Z_j } \rpar } },\cr y_n &=\eta \displaystyle{\sum\limits_{i,j} {\displaystyle{1}{\sigma _i^2 \sigma _j^2 }} \sin \lpar {Z_2 -Z_i } \rpar \sin \lpar {Z_i -Z_j } \rpar B_j \over \sin \lpar {Z_1 -Z_2 } \rpar \sqrt {\displaystyle{A_2 \over 2}\sum\limits_{i,j} {\displaystyle{1 \over \sigma _i^2 \sigma _j^2 }} \sin ^2\lpar {Z_i -Z_j } \rpar } }, \cr \rho _n &=-\eta \xi \displaystyle{\sum\limits_i {\displaystyle{1}{\sigma _i^2 }\sin \lpar {Z_i -Z_1 } \rpar } \sin \lpar {Z_2 -Z_i } \rpar \over \sqrt {A_1 A_2 } }}$$where the summations have been extended over all i and j. As shown in Section 4.3, choosing η and ξ appropriately allows any of the four regions bounded by LoP1 and LoP2 to be selected. For the case of three LoPs these expressions reduce to those given in Equation (15). Since the intercepts, r i, enter through the combinations, B j, the result is independent of the choice of AP as demonstrated in Section 3.
APPENDIX C PROPERTIES OF CONFIDENCE ELLIPSES
The probability density function for the observer's position given in Equation (12) is written in its properly normalised form as:
$${\rm pr}(x,y)= \displaystyle{\sqrt {4ac-b^2} \over 2\pi} \exp \lcub {-\lpar {ax^2+bxy+cy^2+dx+ey+f-p} \rpar } \rcub $$where
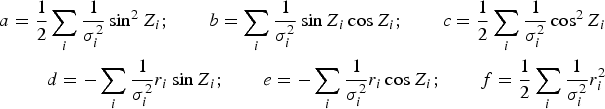$$\eqalign{a=\displaystyle{1 \over 2}\sum\limits_i {\displaystyle{1 \over \sigma _i^2 }\sin ^2Z_i } ;\quad \quad b=\sum\limits_i {\displaystyle{1 \over \sigma _i^2 }\sin Z_i \cos Z_i } ;\quad \quad c=\displaystyle{1 \over 2}\sum\limits_i {\displaystyle{1 \over \sigma _i^2 }\cos ^2Z_i } \cr d=-\sum\limits_i {\displaystyle{1 \over \sigma _i^2 }r_i \sin Z_i } ;\quad \quad e=-\sum\limits_i {\displaystyle{1 \over \sigma _i^2 }r_i \cos Z_i } ;\quad \quad f=\displaystyle{1 \over 2}\sum\limits_i {\displaystyle{1 \over \sigma _i^2 }r_i^2 }}$$and p is defined in Appendix A.
The quadratic argument of the exponential function defines a set of confidence ellipses for the observer's position like those shown in Figure 2. The properties of these confidence ellipses can provide a quantitative measure as to the relative quality of a round of sights. For example, the area of the ellipse at a specified confidence level or the root-mean-square deviations of possible positions from the centre might serve as suitable measures.
Methods for determining the centre, orientation and lengths of the semi-major and semi-minor axis lengths of an ellipse from a quadratic form are well established and described elsewhere (Pettofrezzo, Reference Pettofrezzo1978). Applying these methods and performing the appropriate algebraic reduction yields relatively simple and efficient expressions for these properties in terms of the intercepts, r i, and azimuths, Z i, of an arbitrary number of LoPs.
If the probability of the observer's position falling inside a given confidence ellipse is P then it is known (Abramowitz and Stegun, Reference Abramowitz and Stegun1964. 26.3.21; Daniels, Reference Daniels1951) that the ellipse satisfies the condition:
$$ax^2+bxy+cy^2+dx+ey+f-p=L$$where L = −ln(1 − P). To determine the characteristics of the ellipse it is convenient to start by writing Equation (C2) in the form:
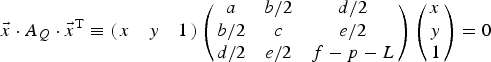$$\vec {x}\cdot A_Q \cdot \vec {x}^{\rm T}\equiv \left(\matrix{x & y & 1} \right) \left(\matrix{a & {b/2} & {d/2} \cr {b/2} & c & {e/2} \cr {d/2} & {e/2} & {f-p-L}} \right) \left(\matrix{x \cr y \cr 1} \right)=0$$ The matrix 
$A_{33} =\left(\matrix{a & {b/2} \cr {b/2} & c} \right)$, whose determinant is the minor or cofactor of the bottom right hand element in matrix A Q, is also needed. Its trace and determinant are:
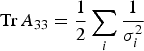$$\hbox{Tr}\,A_{33} =\displaystyle{1 \over 2}\sum\limits_i \displaystyle{1 \over \sigma _i^2}$$
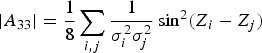$$\vert A_{33} \vert = \displaystyle{1 \over 8} \sum\limits_{i,j} \displaystyle{1 \over \sigma _i^2 \sigma_j^2} \sin^2 \lpar Z_i -Z_j \rpar $$For the particular matrix elements encountered here |A Q| = −L|A 33| which leads to significant simplifications in the results that follow.
The centre of the ellipse is the MPP which lies at:
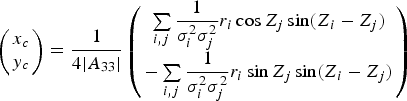$$\left(\matrix{x_c \cr y_c} \right)=\displaystyle{1 \over 4\vert {A_{33} } \vert }\left(\matrix{\sum\limits_{i,j} \displaystyle{1 \over \sigma_i^2 \sigma_j^2} r_i \cos Z_j \sin \lpar Z_i -Z_j \rpar \cr -\sum\limits_{i,j} \displaystyle{1 \over \sigma_i^2 \sigma_j^2} r_i \sin Z_j \sin \lpar Z_i -Z_j \rpar } \right)$$The principal axes of the ellipse are the eigenvectors of A 33 and are found to be:
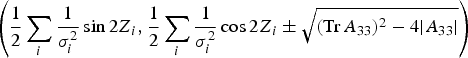$$\left(\displaystyle{1 \over 2} \sum\limits_i \displaystyle{1 \over \sigma_i^2} \sin 2Z_i, \displaystyle{1 \over 2} \sum\limits_i \displaystyle{1 \over \sigma_i^2} \cos 2Z_i \pm \sqrt{\lpar \hbox{Tr}\,A_{33} \rpar^2 - 4 \vert A_{33} \vert } \right)$$or equivalently:
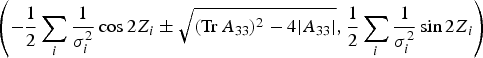$$\left(-\displaystyle{1 \over 2}\sum\limits_i {\displaystyle{1 \over \sigma_i^2 }} \cos 2Z_i \pm \sqrt {\lpar {\hbox{Tr}\,A_{33} } \rpar^2-4\vert {A_{33} } \vert } ,\displaystyle{1 \over 2}\sum\limits_i \displaystyle{1 \over \sigma_i^2} \sin 2Z_i \right)$$which have associated eigenvalues:
$$\lambda_{\pm} = \displaystyle{1 \over 2} \hbox{Tr}\,A_{33} \pm \displaystyle{1 \over 2} \sqrt{\lpar {\hbox{Tr}\,A_{33}} \rpar ^2 - 4\vert A_{33} \vert }.$$
From this it follows that the semi-major axis, 
$a=\sqrt {L/\lambda _- } $, and semi-minor axes, 
$b=\sqrt{L/\lambda _+}$. The area of this ellipse is then 
$\pi ab={\pi L} / \sqrt{\vert A_{33} \vert }$.
The root-mean-square distance of possible positions from the MPP is 
$\sqrt{\displaystyle{1 \over 2}\hbox{Tr}\,A_{33} / \vert A_{33} \vert } $.
Stansfield (Reference Stansfield1947) treats the problem of the probability distribution for a fix generated by an arbitrary number of radio direction finding stations. The problem is transformed into one that is analytically equivalent to the one treated in this appendix. Expressions for the properties of the confidence ellipses are given that are equivalent to those above but without the additional trigonometric reduction that has been performed here.
