1. INTRODUCTION
Over the last twenty years, Global Navigation Satellite Systems (GNSS) have grown to dominate the world for Positioning, Navigation and Timing (PNT) solutions. NATO armed forces have adapted their systems and doctrine with the constant performance and availability of Global Positioning System (GPS) in mind.
The vulnerability and the ease with which this can be exploited has been brought to attention by numerous studies (Last, Reference Last2010; PNT Board, 2010; Volpe, Reference Volpe2001). Despite the awareness of GNSS vulnerability, proficiency in traditional methods used before the GNSS era fade away within the defence organisations and system reliability cannot always be guaranteed. Occurrences of GNSS jamming have been scarce in the past, so there is little desire to change this modus operandi. Moreover, anti-jamming technology and more robust military codes are developing rapidly.
Since GNSS signals are of low power and remain vulnerable, back-up PNT systems are needed in a military environment for different purposes, e.g., for communication systems/data links, infantry, reconnaissance units, surveying, military engineering and artillery. The latter is the topic of research in this paper.
For artillery deployment, GNSS is used in the first place for positioning of the gun. The Gun Location Error (GLE) will always be a parameter in the final accuracy of delivery. This accuracy is called the Mean Point of Impact (MPI) error. Positioning accuracy can also influence the Target Location Error (TLE). Together with the (mean) MPI error and round-to-round error, the aim point is shifted to the point of impact, see Figure 1. When using GPS, the value of MPI is typically around 50 metres for a firing range of 20 kilometres.

Figure 1. Diagram artillery error budget.
As a second navigation system, artillery uses a strap-down Inertial Navigation System (INS). If the GPS position solution differs 150 m radially from the stand alone INS position solution, mostly in the case that GPS is unavailable, the operator has to choose to use INS instead of GPS. As a characteristic of INS, the accuracy will now degrade with time and travelled distance (Titterton and Weston, Reference Titterton and Weston2004). To make sure the GLE stays within limits, the artillery platform must return to a known position after it has driven 5 km; for example, this can be a surveyed landmark or a road intersection. At this known position, INS can be calibrated and starts with a position error equal to the known position's accuracy. This significantly limits the freedom of the artillery's movement. Moreover, when there are no surveyed positions nearby, the GLE will increase even more.
In this paper we study the use of eLORAN (enhanced LOng RAnge Navigation) as a backup artillery position system. After the introduction of eLORAN in Section 2, we study propagation and correction errors for eLORAN that contribute most to its positioning error in Section 3. So called ‘dASF maps’ (differential Additional Secondary Factor maps) are introduced to correct for these propagation errors. Constructing such maps using survey points is the main topic of Section 4. The maps are applied to dynamic measurements to study the eLORAN error reduction for arbitrary tracks in the investigated area. Section 5 discusses the results of the experiment with dynamic measurements.
2. LOW-FREQUENCY NAVIGATION
For artillery positioning in a GNSS-denied environment we studied the use of low-frequency navigation by means of eLORAN. For this purpose a low-cost ‘LORADD’ receiver was used. eLORAN receivers calculate their positions by measuring pseudo ranges, calculated by the difference between Time Of Arrival (TOA) and Time Of Transmission (TOT) of eLORAN pulses coherently modulated on the 100 kHz ground-wave. In this research, position computations have been carried out by means of post-processing the TOAs with a software receiver without using the LORADD receiver. In this manner we have more control and analysing capabilities than by simply using the eLORAN position log from the receiver.
The results in this paper are obtained using post-processing of the classical LORAN signals. Considering the nature of our approach, results would have been the same regardless of the type of LORAN signals that were considered. GPS information sent with the more sophisticated eLORAN system is used to compare the obtained results with ‘ground truth’ information.
For eLORAN, the pseudo-range between receiver r and transmitter a in microseconds can be defined by Equations (1) and (2) below:
where:
r represents the receiver time frame.
τ is the transmitter's time frame.
d ra is the length of the geodesic between the transmitter and the receiver.
c is the speed of light through a vacuum.
P r is internal processing delays of the receiver.
B r is the clock bias of the receiver.
ε represents a random residual error.
ΔUTCa is the unknown clock bias of the transmitter with regard to UTC in the control centre, where eLORAN stations are monitored.
PF, SF and ASF are propagation correction factors that will be discussed in the next section.
Weighted least squares are used to calculate a position from the measured pseudo-ranges (Teunissen, Reference Teunissen2003), using the observation equation as given by:
where:
φ,φ 0,λ and λ 0 are in appropriate dimensions.
t → r is the direction from transmitter to receiver in the receiver's position.
PR calculated is the calculated range between transmitter and an estimated position (φ 0,λ 0). Internal processing delays will merge in the systematic receiver clock bias B.
Consider the initial pseudo range Equation (1), where the receiver has no knowledge of TOT(τ) because it operates in a different timeframe. Because of TOT-control, all received transmitters are assumed to be in the same timeframe (τ) and they transmit with known Ground Repetition Intervals (GRI) and emission delays within a chain. For this reason, if TOT is set to be zero, and the pseudo-range is equal to the TOA in the arbitrary receiver timescale, the unknown true TOT will cancel out as a systematic error together with the receiver clock bias in the least squares solution. The systematic error is now a combination of B r(t),P r and TOT(τ).
All positions in our experiment that were calculated by the software receiver using TOAs with the four strongest eLORAN transmitters available (Figure 2). These transmitters were, in ascending order of signal strength, Sylt (6731Z, 7499M), Lessay (6731M, 7499X), Anthorn (6731Y) and Soustons (6731X). To use ‘all in view’ positioning, transmitters of different chains have to be coupled. The software receiver couples the 6731 chain with 7499M and 7499X through the double rated station Sylt. The transmitter uses two synchronized clocks (well within 10μs) to transmit each signal. The signals are part of two different GRIs that can be coupled by using modulo 10 operations. This is done in the following manner, as at Equation (4):

Figure 2. eLORAN transmitters for North Western Europe.
3. PROPAGATION AND CORRECTION FACTORS
eLORAN receivers assume, in the first instance, that incoming signals have travelled over sea-water paths. The so-called ‘USCG Salt-Water Model’ is then used to compute their positions. This model breaks the velocity of a signal travelling over sea-water down into two components: the Primary Factor (PF) which is the velocity in the Earth's atmosphere, and the sea-water Secondary Factor (SF). The SF, based on the additional delay due to the signal travelling over the sea, is assumed to vary with range (Williams and Last, Reference Williams and Last2000). The software receiver used for this research combines the PF and the SF according to Brunavs’ model (Brunavs, Reference Brunavs1977) at Equation (5):
At this level, the receiver did not take into account that transmitted signals are received after travelling over land. Since the conductivity over land differs from sea paths, it is necessary to determine the additional delays due to the presence of land along the transmission paths. Not taking the additional delays into account will result in a substantial difference in pseudo range computations. These ‘land’ delays are known as ASFs. Since the ASF depends on the fraction of land versus sea in the propagation path, every combination of transmitter and receiver position has its own ASF.
For modelling ASFs in a certain area (A), it is convenient to split the total ASF for each transmitter (ASF tot) into a mean, spatial, and temporal component, as at Equation (6):
where:
x user is the receiver's position.
ASF average(A) is the average ASF value in area A.
The spatial component is an additional value depending on the path the ground wave has to travel to reach the receiver. The mean and spatial component of the ASFs in a certain area can be surveyed or modelled in order to make so called ‘ASF-maps’ (Williams and Last, Reference Williams and Last2000).
The temporal component is more complicated. Due to the time dependency of this component, a map cannot be produced. Factors affecting the bias in this include changes in surface impedance of the ground due to climate and weather, by influences of weather, climate, and ground elevation on the index of refraction of air at the surface of the ground, see (Doherty et al., Reference Doherty, Johler and Campbell1979).
It might be possible to estimate some periodic trends, but measuring them gives better results. By using a ‘differential eLORAN’ station (dLORAN), temporal variation can be determined by analysing the difference between a known position and a measured position.
One of the main objectives of this paper is to map mean and spatial ASF variation in an area typically used for artillery deployment. To obtain true ASFs in a certain area, differences between true and measured pseudo-ranges have to be computed. However, due to the arbitrary timescale in a low-cost receiver, this seems impossible as knowledge of the transmitter and receiver clock error and internal delays is necessary. For this reason we use the concept of differential ASFs. First we take:
with variables as in Equation (2).
Next, the transmitter closest to the receiver is assumed to have the smallest ASF, which is Sylt (7499M) in our experiment. Its corresponding pseudo-ASF is subtracted from the pseudo-ASFs from all other pseudo-ASFs, computed from other transmitters in the receiver, i.e., at Equation (8):
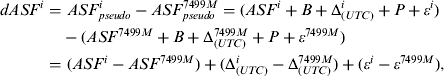 $$\eqalign{dASF^i = &\ ASF_{\,pseudo}^i - ASF_{\,pseudo}^{7499M} = (ASF^i + B + \Delta _{(UTC)}^i + P + \varepsilon ^i ) \cr & - (ASF^{7499M} + B + \Delta _{(UTC)}^{7499M} + P + \varepsilon ^{7499M} ) \cr = &\ (ASF^i - ASF^{7499M} ) + (\Delta _{(UTC)}^i - \Delta _{(UTC)}^{7499M} ) + (\varepsilon ^i - \varepsilon ^{7499M} ),} $$
$$\eqalign{dASF^i = &\ ASF_{\,pseudo}^i - ASF_{\,pseudo}^{7499M} = (ASF^i + B + \Delta _{(UTC)}^i + P + \varepsilon ^i ) \cr & - (ASF^{7499M} + B + \Delta _{(UTC)}^{7499M} + P + \varepsilon ^{7499M} ) \cr = &\ (ASF^i - ASF^{7499M} ) + (\Delta _{(UTC)}^i - \Delta _{(UTC)}^{7499M} ) + (\varepsilon ^i - \varepsilon ^{7499M} ),} $$where i is an index number to indicate the transmitter.
By using dASFs, the common receiver clock error and internal delays cancel out and only a combined transmitter clock error and residual remains. This makes the dASFs useful for other receivers. The dASFs can be used in the same manner as stated in Equation (6), where they represent the spatial component, when the average dASF of the area is subtracted and the temporal component is set to zero during the time of the survey. We observed that the dASFs represented an ASF value with respect to a reference ASF. This makes it hard to see the delay effects of land or sea masses, scenery and construction. Of course, by construction, the dASF value of transmitter Sylt 7499M itself is zero, but this signal can still be used for positioning.
4. STATIC MEASUREMENTS FOR dASF MAPS
In our study, the performance of eLORAN is examined in a typical environment for artillery deployment. The Oldebroekse Hei is a heath land area in the mid-Eastern part of the Netherlands; it was chosen because of its soil and scenery (sand and forest) and relatively long transition distance from sea-to-land and from urban areas. Here, static measurements were made using an E-field antenna setup to generate dASF maps that were used for correcting dynamic measurements in a second experiment. To study temporal variations in eLORAN positions, the experiments were conducted for 24 hours on two occasions during a 17 day period. For both static and dynamic experiments an antenna pole was fixed to the back of a Mercedes-Benz 290 GD (MB) modified for Netherlands’ army purposes.
As part of our research we examined temporal fluctuations of the total ASF on the Oldebroekse Hei. The ASFtemporal has a diurnal component, but also varies over longer periods of time. The electrical conductivity of the surface is the prime factor for this bias. Furthermore, seasonal effects are periodic, while short term effects can be capricious, depending on the atmosphere. The diurnal component is examined by a 24 hour measurement. During 24 hours eLORAN positions were logged at one static position. This bias does not necessarily degrade eLORAN's performance in the area of operations, because it can be partly solved for if a differential eLORAN beacon (dLORAN) is used.
In this paper we concentrated on non-temporal ASF corrections using dASF maps. Therefore, we did not elaborate results for temporal measurements here, but refer to (Griffioen, Reference Griffioen2011) for the interested reader.
Static eLORAN measurements took place at seven different surveyed points on the Oldebroekse Hei within an area of approximately 4 km2 with mean mutual distances (to nearest neighbouring points) of approximately 1 km. The area with its survey points has been depicted in Figure 3. These positions have been surveyed by dedicated authorities using triangulation techniques. However, since these points were surveyed several years ago without using the most accurate techniques presently available, all seven positions were surveyed using Real-Time Kinematic (RTK) GPS. For each survey point 200 eLORAN positions were measured and compared to the corresponding RTK GPS positions.

Figure 3. The Oldebroekse Hei with survey points.
In Figure 4, the results of the 24 hour survey have been plotted. Notable are a few positions in the North-West and South-East corner that seem to have an exceptionally large error, and a small cloud of positions North-East of the mean position. Studying the results in more detail, it turns out that the South-East outliers were measured just before a heavy rain shower at the measurement site. Apparently, this phenomenon changed the electrical conductivity of the surface in such a way that a position shift occurred. The other North-West outliers appear to be related to a battery switch. The overall 24 hour R95 precision with the LORADD-SP receiver using PF and SF corrections is 12·2 metres, which is comparable with results in former studies (Pelgrum, Reference Pelgrum2006; Oonincx and Scheele, Reference Oonincx and Scheele2010). We observe that although the Oldebroekse Hei is not close to the sea and is surrounded by urban areas, this is not noticeable in the level of position achieved. Furthermore, from Figure 4 it seems that temporal issues in this 24 hour survey are not of significant influence.

Figure 4. E-field static position errors from mean position.
Mean values of the static measurements have been used to computed dASFs, as given in Equation (7) for the seven survey points. Next, the derived dASF values are used for interpolation as grid values. Several interpolation schemes were tested in our experiments and all performed similarly.
As mentioned before, at all survey points 200 eLORAN positions were computed using raw data (arrival times). Figure 5 provides a visual impression of these measurements with respect to the RTK GPS positions of the points. Taking the mean of the measurements 42 dASF values have been computed in post-processing. These 42 (6 transmitters, 7 survey points) dASF values are used for linear interpolation, yielding 6 dASF maps to be used for correcting eLORAN positions in dynamic measurements.
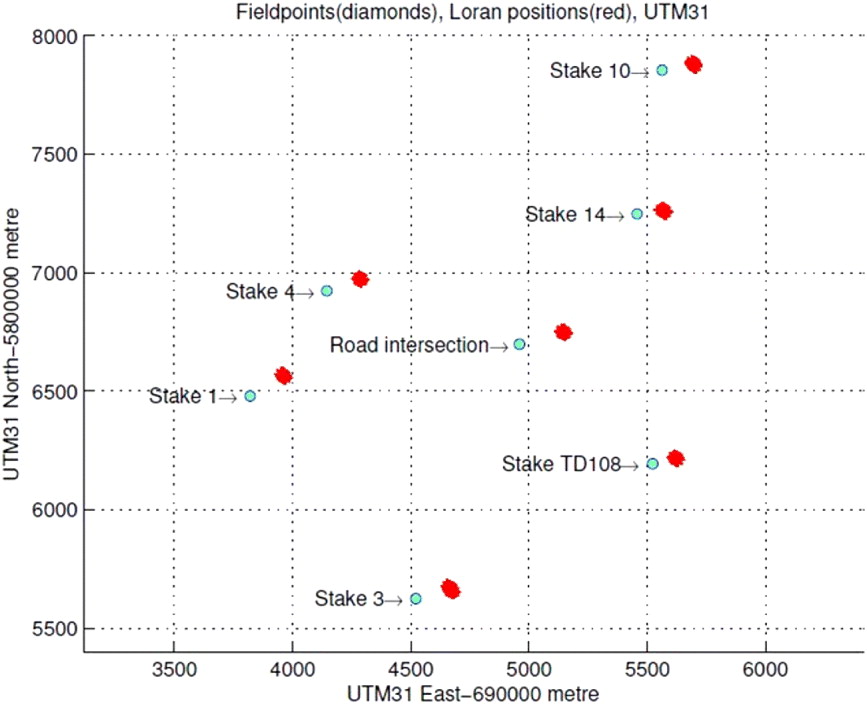
Figure 5. Survey points and corresponding 200 LORAN position clouds.
An example of a created dASF map using linear interpolation for the transmitter Lessay 6731M has been depicted in Figure 6. The mapping contains dASF values in microseconds for an area spanned by the survey points. As stated before, the dASFs represent an ASF value with respect to a reference ASF. This makes it hard to see the delay effects of land or sea masses, scenery and construction in the dASF maps.

Figure 6. dASF map of the Lessay transmitter with ‘linear’ interpolation method.
Studying all created dASF maps, a peak appears in the proximity of the road intersection, see Figure 3. Apparently, spatial dASF values were higher at that spot compared to surveyed positions closer to the area's edge. Spatial dASF values in the whole area increase towards this central point because of interpolation. This could be a good representation of the course of the spatial dASFs, but only if the road intersection's higher values are not associated with a rather local anomaly.
To find out how the road intersection's surveyed point influences the total accuracy, it is left out in a new set of dASF maps. Obviously, by not taking the road intersection survey point into account the resolution decreases and a lower accuracy can be expected. Experiments (Griffioen, Reference Griffioen2011) showed that the accuracy did not degrade, which means that grid resolution is so low that it does not cover the spatial dASF irregularity sufficiently. In other words, with a higher resolution rate of survey points, the road intersection value would be surrounded by a number of surveyed points that would smooth the transition from the outer points to the more central road intersection.
5. DYNAMIC MEASUREMENTS
Dynamic measurements with the antenna placed on top of the Military Platform (MB) have taken place twice in a 17 day period. During the first survey, the MB was towed by another MB to reduce interference with the MB's electronics (Figure 7). For the second survey a different laptop and no additional MB was used. This reduced the interference substantially. As a result the signal's strength was much better in terms of Signal to Noise Ratio (SNR) during the second survey. In the analysis of our results this phenomenon turned out to yield higher position precision. Therefore, we will focus in this paper on the results of the second survey (Dynamic 2) and only mention similar results from the first survey.

Figure 7. MB with E-field measurement set-up pulled by second MB in the first survey.
During the dynamic measurements we kept a log of TOAs, received signal strengths, signal to noise ratios and unassisted eLORAN and DGPS positions. With the software receiver eLORAN positions have been calculated by post-processing. These positions have been corrected with the dASF maps for every transmitter, observed after linear interpolation at the seven survey points.
The post-processed eLORAN positions for the track have been compared with dGPS positions from the Eurofix signal in the LORADD receiver. Figure 8 shows the results of the second dynamic survey. As can be observed, the dASF corrected eLORAN position give good results in most parts of the survey. In the proximity of the road intersection position, average errors are the highest. Theoretically, this larger error is not expected, since the track crosses a surveyed point and true spatial dASF values are assumed to be quite similar to the measured values. As we discussed before, larger errors in the road intersection surroundings are due to the numerical interpolation scheme and its corresponding geometry.

Figure 8. LORAN and GPS positions of dynamic 2 with linear dASF maps.
For this dynamic survey, an analysis of the results showed the following errors in metres in Table 1, after using the interpolated dASF maps:
Table 1. Errors in metres, after using the interpolated dASF map.

Figure 9 shows the various errors as a function of the time during the survey. The platform started at zero seconds at position (3500,6700) North West of Stake (point) 1 in Figure 8. The very large maximum error of 180 metres corresponds to an area just after passing Stake (point) 1. There, eLORAN positions show large errors along the direction of the path, coinciding with a low SNR. Signal strength is significantly lower at this spot along the track, which can be explained by a local distortion source of the nearby railway's high voltage power transformers; see also (Pelgrum, Reference Pelgrum2006). The second peak in the dynamic error around epoch 100 is related to the road intersection point that leads to large interpolation errors in the dASF maps as observed before.

Figure 9. dASF Radial error for the second dynamic survey with mean and R95 value.
Although the survey yielded interesting results on eLORAN-based navigation using dASF maps, the initial goal of our research was to investigate how eLORAN can be used for artillery deployment in a GNSS denied environment. In particular, we concentrated on the question of how a GLE with eLORAN positioning would influence the MPI error, see Figure 1. As mentioned in Section 1, the value of MPI with GPS positioning is typically around 50 metres for a firing range of 20 kilometres. Based on our survey, Table 2 summarises the results.
Table 2. GLE with eLORAN positioning would influence the MPI error.

The ‘first round, fire for effect’ performance (60·2 metres) has decreased by 20·4% compared to the original 50 metres. Furthermore, the mean MPI error is now reached 5·2 kilometres earlier. We observe that a larger GLE plays a more dominant role at short distance than at firing distances that approach the platform's maximum firing range of 40 kilometres. Also in the analysis so far, the TLE is left out. This bias can be treated the same way as the GLE.
6. CONCLUSIONS
In this paper we showed that the static performance of eLORAN (enhanced LOng RAnge Navigation) in a land environment is not different from former studies in other areas closer or at sea. By using dASF maps (differential Additional Secondary Factor maps) based on a relatively small number of interpolation points (grid resolution of ±1 km) we achieved a measured dynamic performance is 33·6 metres mean radial, with 65·9 metres R95. We expect a substantial increase in performance if more interpolation points in a mathematically optimised geometry are surveyed. However, for military operations an ‘ideal’ set of survey points may not be available due to limited accessibility of the area.
For firing accuracy, measured eLORAN performance creates a much larger gun location error than by using GPS. With an increase by 20·4% of the 50 metre error constraint at 20 kilometres firing range eLORAN's performance reduction may still be acceptable as backup. Moreover, increasing the number of survey points may even yield better results for the firing range errors in case eLORAN is used as a GPS backup. Whether the reduction in performance is acceptable for artillery purposes was not a topic addressed in this paper.
ACKNOWLEDGEMENT
We would like to thank C. A. Scheele for helpful discussions and the military personal of the Royal Netherlands Army for their help with carrying out the experiments.












