Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Medvedev, S. Yu.
Ivanov, A. A.
Martynov, A. A.
Poshekhonov, Yu. Yu.
Konovalov, S. V.
and
Polevoi, A. R.
2016.
Influence of plasma pedestal profiles on access to ELM-free regimes in ITER.
Plasma Physics Reports,
Vol. 42,
Issue. 5,
p.
472.
Cooper, W A
Graves, J P
Duval, B P
Sauter, O
Faustin, J M
Kleiner, A
Lanthaler, S
Patten, H
Raghunathan, M
Tran, T-M
Chapman, I T
and
Ham, C J
2016.
Three-dimensional magnetohydrodynamic equilibrium of quiescent H-modes in tokamak systems.
Plasma Physics and Controlled Fusion,
Vol. 58,
Issue. 6,
p.
064002.
Brunetti, D.
Graves, J.P.
Lazzaro, E.
Mariani, A.
Nowak, S.
Cooper, W.A.
and
Wahlberg, C.
2018.
Analytic stability criteria for edge MHD oscillations in high performance ELM free tokamak regimes.
Nuclear Fusion,
Vol. 58,
Issue. 1,
p.
014002.
Kleiner, A.
Graves, J.P.
Cooper, W.A.
Nicolas, T.
and
Wahlberg, C.
2018.
Free boundary 3D ideal MHD equilibrium calculations for non-linearly saturated current driven external kink modes in tokamaks.
Nuclear Fusion,
Vol. 58,
Issue. 7,
p.
074001.
Brunetti, Daniele
Graves, J. P.
Lazzaro, E.
Mariani, A.
Nowak, S.
Cooper, W. A.
and
Wahlberg, C.
2018.
Analytic study on low- external ideal infernal modes in tokamaks with large edge pressure gradients.
Journal of Plasma Physics,
Vol. 84,
Issue. 2,
Brunetti, D.
Graves, J. P.
Lazzaro, E.
Mariani, A.
Nowak, S.
Cooper, W. A.
and
Wahlberg, C.
2019.
Excitation Mechanism of Low-
n
Edge Harmonic Oscillations in Edge Localized Mode-Free, High Performance, Tokamak Plasmas.
Physical Review Letters,
Vol. 122,
Issue. 15,
Fenstermacher, M.E.
Baylor, L.R.
de la Luna, E.
Dunne, M.G.
Huijsmans, G.T.A.
Kirk, A.
Laggner, F.M.
Osborne, T.H.
Paz-Soldan, C.
Saarelma, S.
Snyder, P.B.
Viezzer, E.
Becoulet, M.
Burrell, K.H.
Cathey, A.
Chen, X.
Hoelzl, M.
Hughes, J.W.
Maingi, R.
Nelson, A.O.
Urano, H.
Wolfrum, E.
Xu, X.Q.
Diallo, A.
Frassinetti, L.
Futatani, S.
Gil, L.
Groebner, R.
Happel, T.
Kim, S.H.
King, J.
Labit, B.
Lang, P.T.
Liu, Y.Q.
Liu, Z.X.
Lunsford, R.
Park, G.Y.
Sheikh, U.
Suttrop, W.
Vanovac, B.
Wilcox, R.S.
Wingen, A.
and
Zhang, T.
2025.
Progress in pedestal and edge physics: Chapter 3 of the special issue: on the path to tokamak burning plasma operation.
Nuclear Fusion,
Vol. 65,
Issue. 5,
p.
053001.
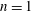 $n=1$ distortions when the edge bootstrap current is large and higher
$n=1$ distortions when the edge bootstrap current is large and higher  $n$ corrugations when this current is small. Linear ideal MHD stability analyses confirm the nonlinear saturated ideal kink equilibrium states produced and we can identify the Pfirsch–Schlüter current as the main linear instability driving mechanism when the edge pressure gradient is large. The dominant non-axisymmetric component of this Pfirsch–Schlüter current drives a near resonant helical parallel current density ribbon that aligns with the near vanishing magnetic shear region caused by the edge bootstrap current. This current ribbon is a manifestation of the outer mode previously found on JET (Solano 2010). We claim that the equilibrium corrugations describe structures that are commonly observed in quiescent H-mode tokamak discharges.
$n$ corrugations when this current is small. Linear ideal MHD stability analyses confirm the nonlinear saturated ideal kink equilibrium states produced and we can identify the Pfirsch–Schlüter current as the main linear instability driving mechanism when the edge pressure gradient is large. The dominant non-axisymmetric component of this Pfirsch–Schlüter current drives a near resonant helical parallel current density ribbon that aligns with the near vanishing magnetic shear region caused by the edge bootstrap current. This current ribbon is a manifestation of the outer mode previously found on JET (Solano 2010). We claim that the equilibrium corrugations describe structures that are commonly observed in quiescent H-mode tokamak discharges.