Article contents
Diffusive scattering of energetic electrons by intense whistler-mode waves in an inhomogeneous plasma
Published online by Cambridge University Press: 06 January 2023
Abstract
Electron resonant interactions with electromagnetic whistler-mode waves play an important role in electron flux dynamics in various space plasma systems: planetary radiation belts, bow shocks, solar wind and magnetic reconnection regions. Two key wave characteristics determining the regime of wave–particle interactions are the wave intensity and the wave coherency. The classical quasi-linear diffusion approach describes well electron diffusion by incoherent and low-amplitude waves, whereas the nonlinear resonant models describe electron phase bunching and trapping by highly coherent intense waves. This study is devoted to the investigation of the regime of electron resonant interactions with incoherent but intense waves. Although this regime is characterized by electron diffusion, we show that diffusion rates scale linearly with the wave amplitude, $D\propto B_w$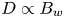 , in contrast to the quasi-linear diffusion scaling $D_{QL}\propto B_w^2$
, in contrast to the quasi-linear diffusion scaling $D_{QL}\propto B_w^2$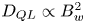 . Using observed wave amplitude distributions, we demonstrate that the quasi-linear diffusion model significantly overestimates electron scattering by incoherent, but intense whistler-mode waves. We discuss the results obtained in the context of simulations of long-term electron flux dynamics in space plasma systems.
. Using observed wave amplitude distributions, we demonstrate that the quasi-linear diffusion model significantly overestimates electron scattering by incoherent, but intense whistler-mode waves. We discuss the results obtained in the context of simulations of long-term electron flux dynamics in space plasma systems.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 11
- Cited by



